ABSTRACT
There are many nonlinear vibration problems of mechanical structures because of various reasons such as geometric parameters, impact loads, or property of materials. One simple solution for the suppression of nonlinear structural vibration is input shaping that generates a command signal to cancel its vibration. However, a motion platform to evaluate the performance of input shapers for nonlinear vibration is rare. This paper presents the evaluation of input shaping methods for the nonlinear vibration system using a Furuta pendulum. First, the mathematical model of the Furuta pendulum is introduced and its nonlinear vibration characteristic is analyzed. Then, commands for canceling the nonlinear vibration of the Furuta pendulum are generated with various input shapers such as ZV, ZVD, and ZVDD. Finally, we illustrate the effects of input shapers on the nonlinear Furuta pendulum by comparing the pendulum overshoot, settling time, and vibration-reduction ratio. The Furuta pendulum is shown to be a good motion platform to evaluate input shaping methods for nonlinear vibration systems.
-
KEYWORDS: Nonlinear vibration, Input shaping, Furuta pendulum
-
KEYWORDS: 비선형 진동, 입력 성형, 후루타 펜둘럼
NOMENCLATURE
Damper ratio of pendulum link
Gravitational acceleration
Inertia moment of pendulum link
Kinetic energy of pendulum link
Starting time of ith command
1. Introduction
Over decades, numerous approaches to suppress linear or nonlinear vibration systems have been studied.
1-5 These approaches can be classified into three main categories. The first one is to fundamentally avoid the excitation source by introducing special kinematic structure or force balancing. The second one is to cut the vibration transfer path by adding some devices or changing structures. The last one is to actively control the vibration with sensor or actuators such as feedback and feedforward controls.
There are many nonlinear vibration problems of mechanical structures or systems caused by various factors such as geometry, load condition, and materials.
6,7 Although nonlinear vibration problems could be dealt with linear approaches, nonlinear effects cannot be neglected under cases of substantial amplitude or excitation. That is, the system dynamic variation due to its nonlinearity should be tackled with robust or nonlinear control.
8
A simple solution for vibration problem is input shaping, which generates command signal to cancel its own vibration.
9-14 The effectiveness of input shaping has been proved in many engineering applications. However, numerical simulation or parameter estimation was required for input shaping of nonlinear vibration since input shaping is developed based on linear system theory.
12,13 In addition, a motion platform to evaluate various input shapers for nonlinear vibration is very rare.
Furuta pendulum is a rotational inverted pendulum used to study complex nonlinear oscillation based on control theory.
15-19 Furuta pendulum consists of a driven arm rotating in the horizontal plane and a pendulum attached to the arm that is free to rotate in the vertical plane. Consequently, Furuta pendulum is under-actuated and extremely nonlinear due to the gravitational forces and the coupling from the Coriolis and centripetal force. Many papers focused on swing-up control of Furuta pendulum considering its complex nonlinear features.
This paper presents evaluation of input shaping methods for the nonlinear vibration system using a Furuta pendulum. The Furuta pendulum of this paper is operated as a nonlinear motion platform at the stable uninverted position. First, the mathematical model of the Furuta pendulum is introduced and its nonlinear vibration characteristic is analyzed. Then, commands for cancelling the nonlinear vibration of the Furuta pendulum are generated with various input shapers such as ZV (Zero Vibration), ZVD (Zero Vibration Derivative), and ZVDD (Zero Vibration Double Derivative). Finally, we illustrate the effects of input shapers on the nonlinear Furuta pendulum by comparing the pendulum overshoot, settling time and vibration-reduction ratio. The Furuta pendulum is shown to be a good motion platform to evaluate input shaping methods for nonlinear vibration system.
2. Furuta Pendulum Model
2.1 Mathematical Model
Although Furuta pendulum is normally used to study complex nonlinear controls for swinging up the pendulum link into the inverted position, the Furuta pendulum of this study is a nonlinear motion platform of the under-actuated pendulum link swinging around the stable uninverted position.
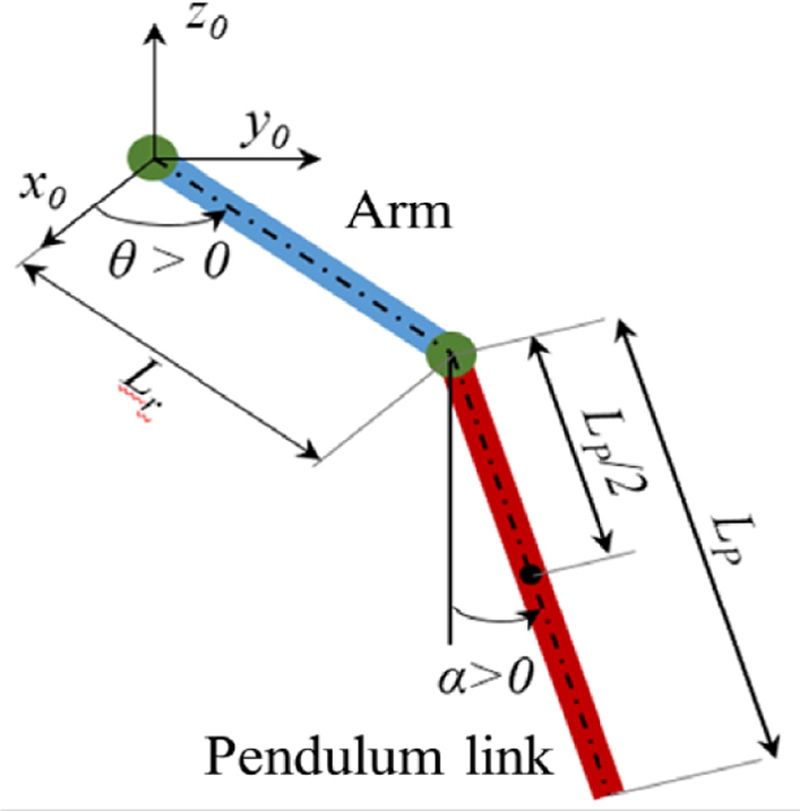
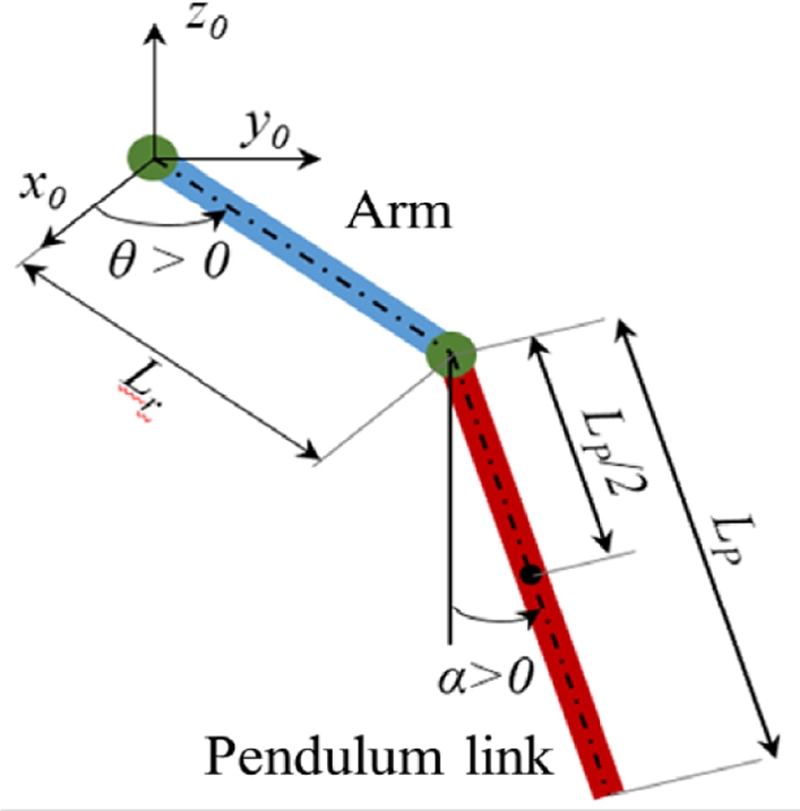
Compared with a conventional pendulum based on linear motion and limited in space of rail, Furuta pendulum uses an unlimited rotational input motion. Schematic diagram of the Furuta pendulum is shown in
Fig. 1. The arm of length
Lr is driven by angle
θ with a DC motor and one end of the arm is connected to the pendulum link of length
LP. The arm angle
θ and the pendulum angle
α are zero at the uninverted vertical position of the pendulum and increase as it rotates in the counter-clockwise (CCW) direction.
Fig. 1Schematic diagram of the Furuta pendulum
Equations of motion (EOM) for the pendulum can be derived with Euler-Lagrange equation, as shown in
Eq. (1).
15 Kinetic energy
T is the sum of kinetic energies of both the arm and the pendulum link. In addition, the potential energy is given by the potential of the pendulum link.
F is the damping term related to the arm and the pendulum link, and
u is input of motor. The resulting derived EOM of the Furuta pendulum has severe nonlinearities, as shown in
Eq. (2). The motion of the arm is highly coupled with the pendulum link motion.
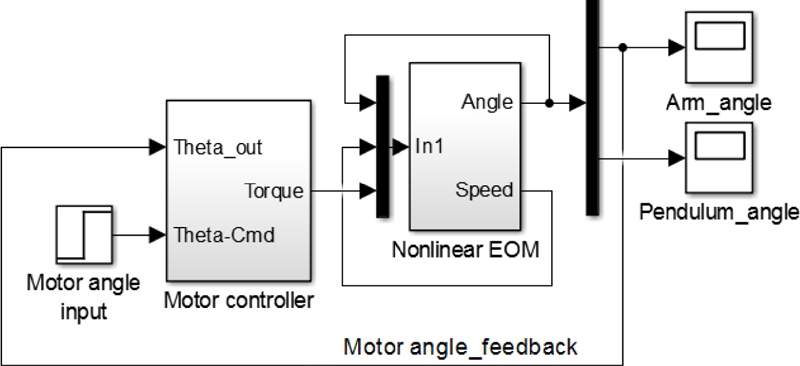
Fig. 2 shows a simulation model consisting of a DC motor controller and the derived EOM of the Furuta pendulum. The parameters of the simulation model are summarized in
Table 1. For the simplicity, the DC motor is approximated as a first order system with torque and time constants. In addition, a PD control is used to control the DC motor.
Fig. 2Simulation model of the Furuta pendulum
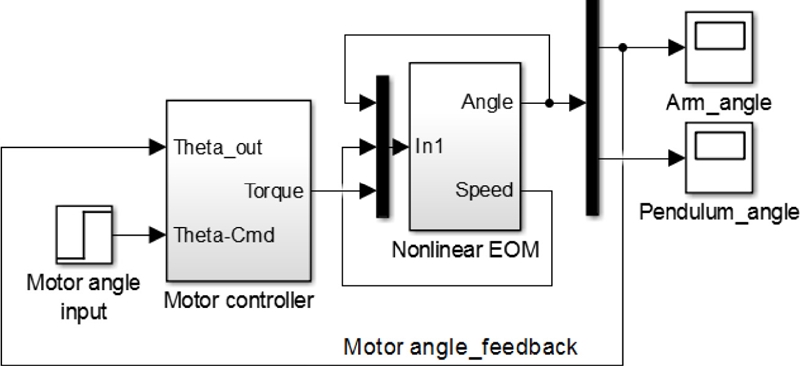
Table 1Parameters of the Furuta pendulum20
Table 1
|
Parameters |
Value |
|
Length of arm Lr [m] |
0.085 |
|
Length of pendulum link LP [m] |
0.129 |
|
Moment of inertia of arm Jr [kg.m2] |
5.72 × 10-5
|
|
Moment of inertia of pendulum link JP [kg.m2] |
1.33 × 10-4
|
|
Damping of arm Dr [Nms/rad] |
2 × 10-4
|
|
Damping of pendulum link DP [Nms/rad] |
3 × 10-4
|
|
Mass of pendulum link mP [kg] |
0.024 |
|
Gravitational accerelation g [m/s2] |
9.81 |
|
Motor toque constant K [Nm/A] |
23.2 |
|
Motor time constant τ [sec] |
0.126 |
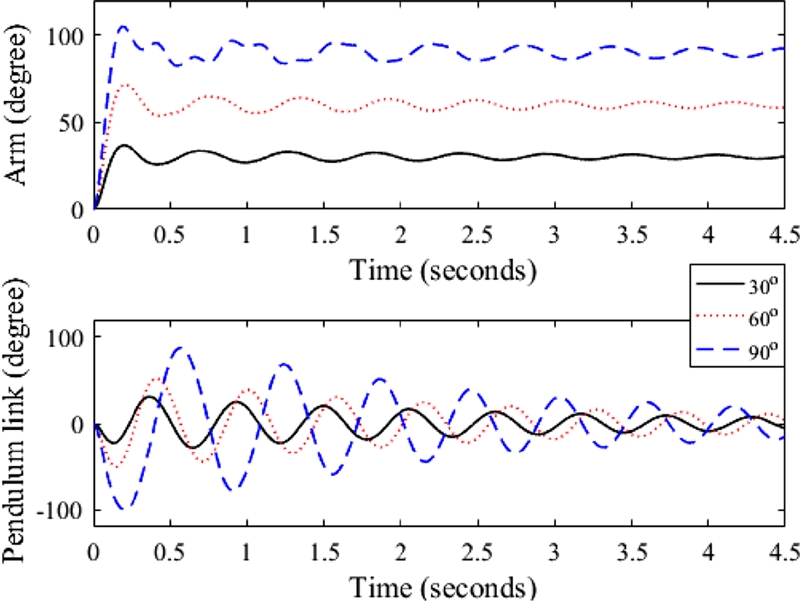
Simulations with various arm or motor reference commands are performed to investigate the nonlinear vibration characteristic of the Furuta pendulum. The resulting arm and pendulum link, for cases of motor reference commands of 30, 60 and 90 degrees, are shown in
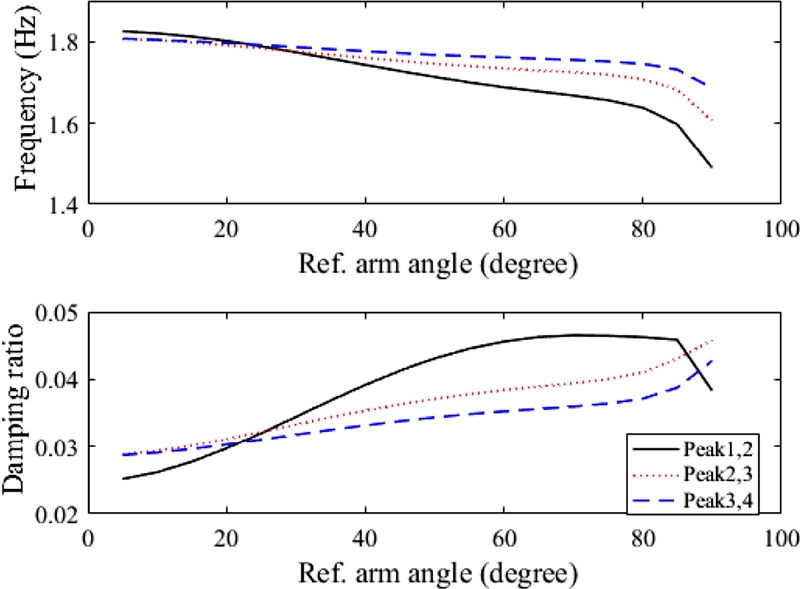
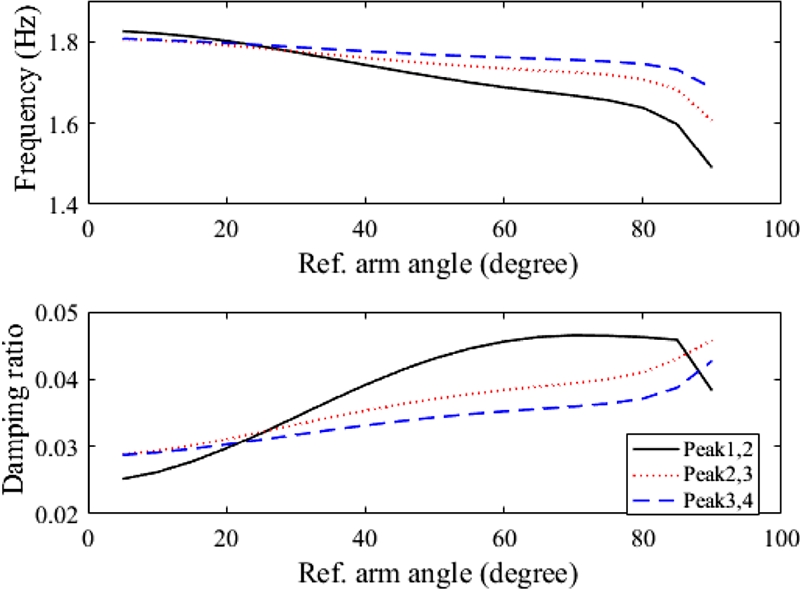
Fig. 3. As the reference arm angle increases, nonlinear effects such as frequency variation are also greatly affected. In particular, the vibration suppression is not simple in the case of large reference arm angle like 90 degrees. In addition, the vibration frequencies (The Inverse of Time between Following Peaks) and damping (Logarithmic Decrement of Following Peaks) of the pendulum link with various magnitudes of reference arm angles are shown in
Fig. 4. The damping decreases as the reference arm angle increases and time passes by. On the other hand, the frequency increases as the reference arm angle decreases and time passes by. In particular, the abrupt changes of both vibration frequency and damping occur in the case of large reference arm angle like 90 degrees. That is, the Furuta pendulum is a suitable motion platform.
Fig. 3Nonlinear vibration characteristics of the Furuta pendulum with various arm reference commands
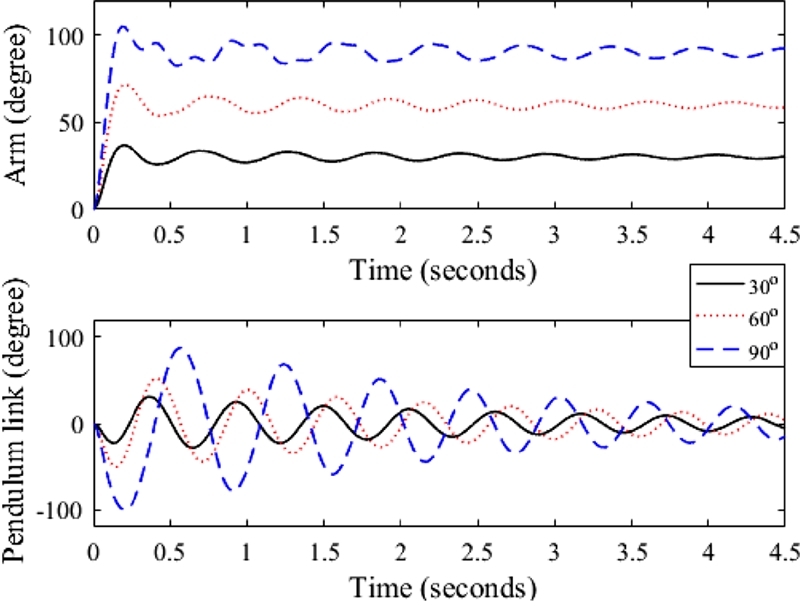
Fig. 4Vibration frequency and damping of the Furuta pendulum link with various arm reference commands
3. Experiments
3.1 Experimental Set-Up
Experimental set-up consists of Furuta pendulum with QUBE-Servo
20 and NI myRIO,
21 as shown in
Fig. 5. The Furuta pendulum consists of the QUBE-Servo with DC servo, an arm with an optical encoder and a pendulum link. The QUBE-Servo includes a brushed DC motor with an optical encoder, a PWM amplifier, and an interface module. The DC motor is directly controlled with NI myRIO or an embedded real-time hardware that has both analog and digital-in/out, FPGA and ARM Cortex-A9 processor.
Fig. 5Experiment set-up of the Furuta pendulum

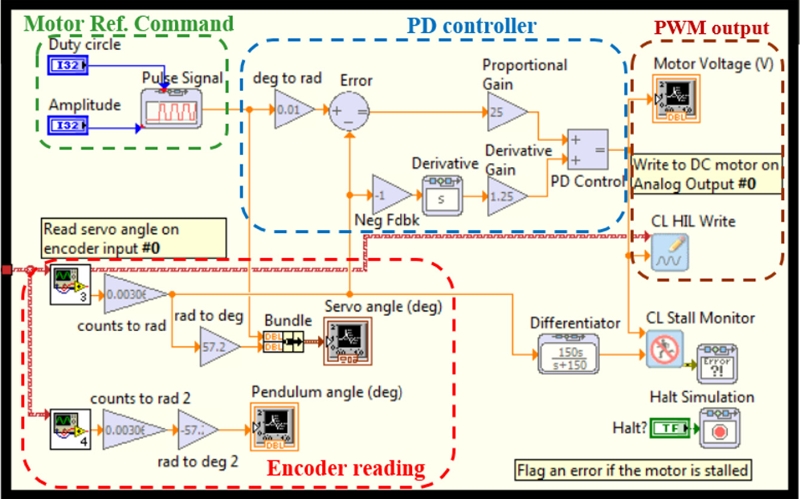
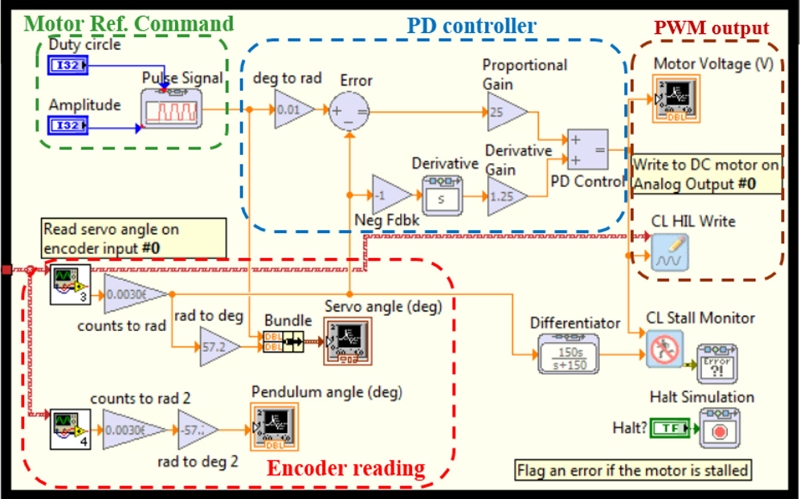
A control system is built under NI Labview environment with a rapid control prototyping toolkit.
22,23 The control system consists of motor reference command, PD controller, PWM output and encoder reading, as shown in
Fig. 6. Series of pulse signals with different amplitudes and widths are generated for the motor reference commands or input shaping methods. In addition, a PD controller (
KP = 25 and
KD = 1.25) is used for DC motor servo control.
Fig. 6Control system for Furuta pendulum in NI Labview
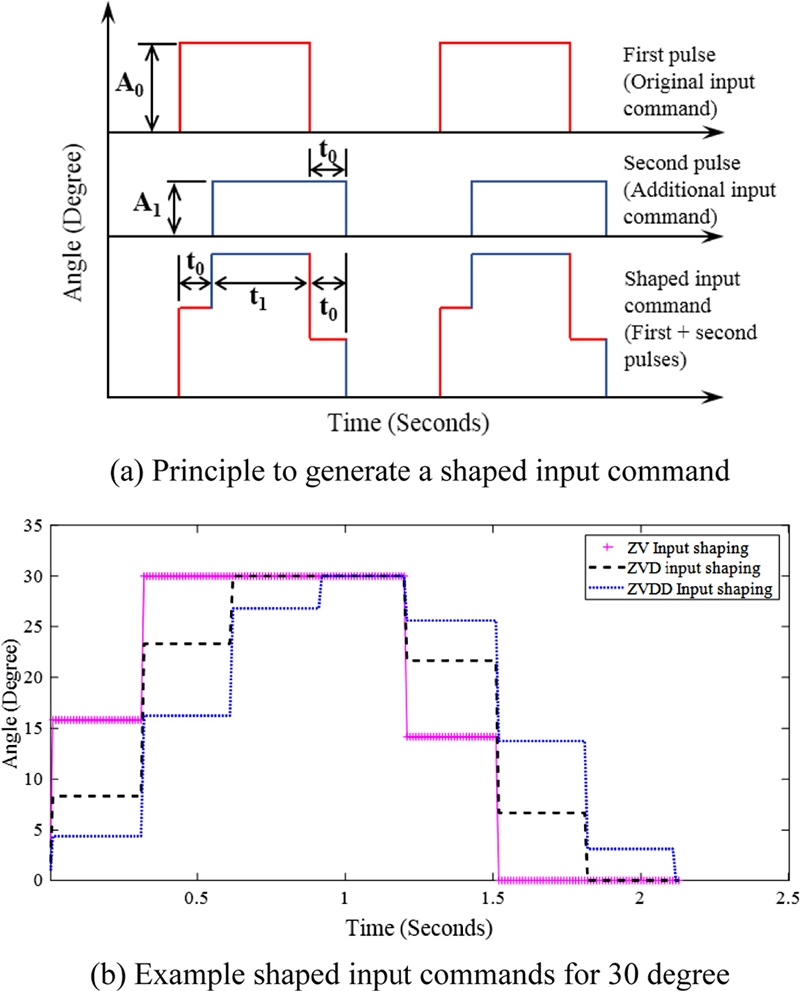
Based on vibration frequency and damping ratio, shaped input commands of ZV, ZVD and ZVDD are generated for the reference arm angle of 30, 60 and 90
o, respectively. Set of pulse signals with different amplitudes and widths are combined for the shaped input commands, as shown in
Fig. 7(a). The shaped input of the ZV consists of two pulses with different amplitudes and widths and the second pulse
A1 applied with later time
t0 cancels the vibration caused by the first pulse
A0. The resulting shaped inputs of the ZV, ZVD, ZVDD for reference arm angle of 30
o are illustrated in
Fig. 7(b). The parameters of pulses are determined based on vibration frequency and damping of the Furuta pendulum. The equation for parameters of the shaped inputs commands of ZV, ZVD, ZVDD is illustrated in
Table 2.
Fig. 7The shaped input commands
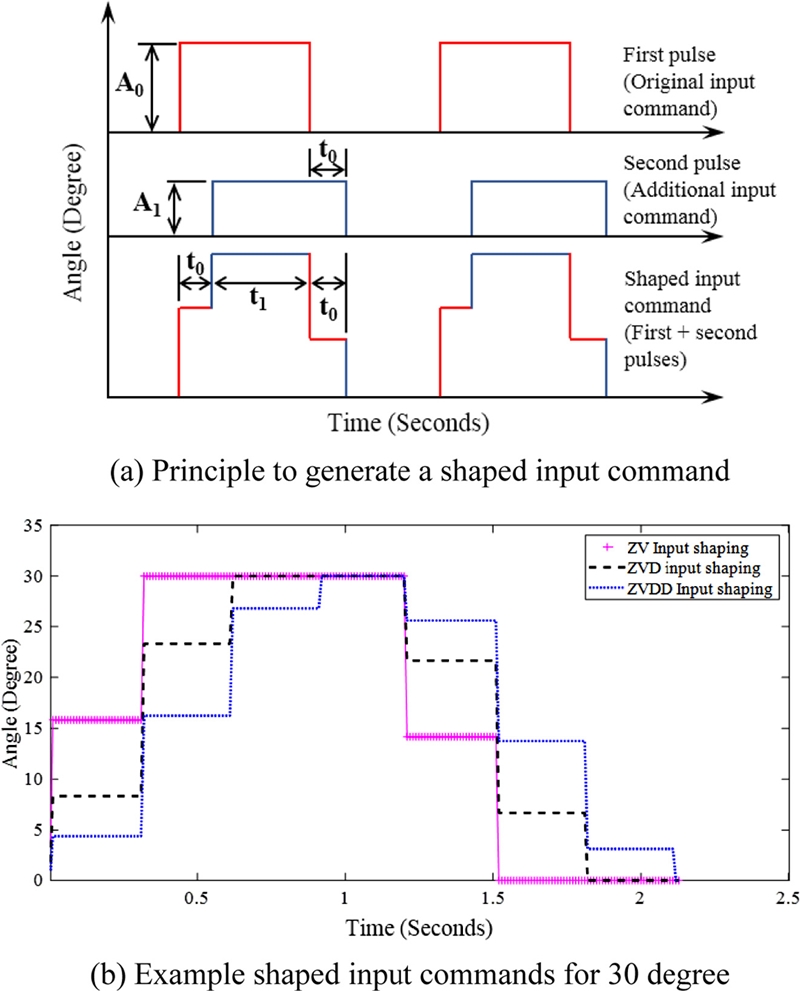
Table 2Equations for the shaped input commands
Table 2
|
Input shapers |
Equation |
|
ZV* (i = 2) |
Aiti=11+κκ1+κ00.5Td
|
|
ZVD** (i = 3) |
Aiti=11+κ22κ1+κ2κ21+κ200.5TdTd
|
|
ZVDD***(i = 4) |
Aiti=11+κ33κ1+κ33κ21+κ3κ31+κ300.5TdTd1.5Td
|
|
Td=2πωd, -ζπ1-ζ2Modal parameters of vibrationκ=e
|
3.2 Results
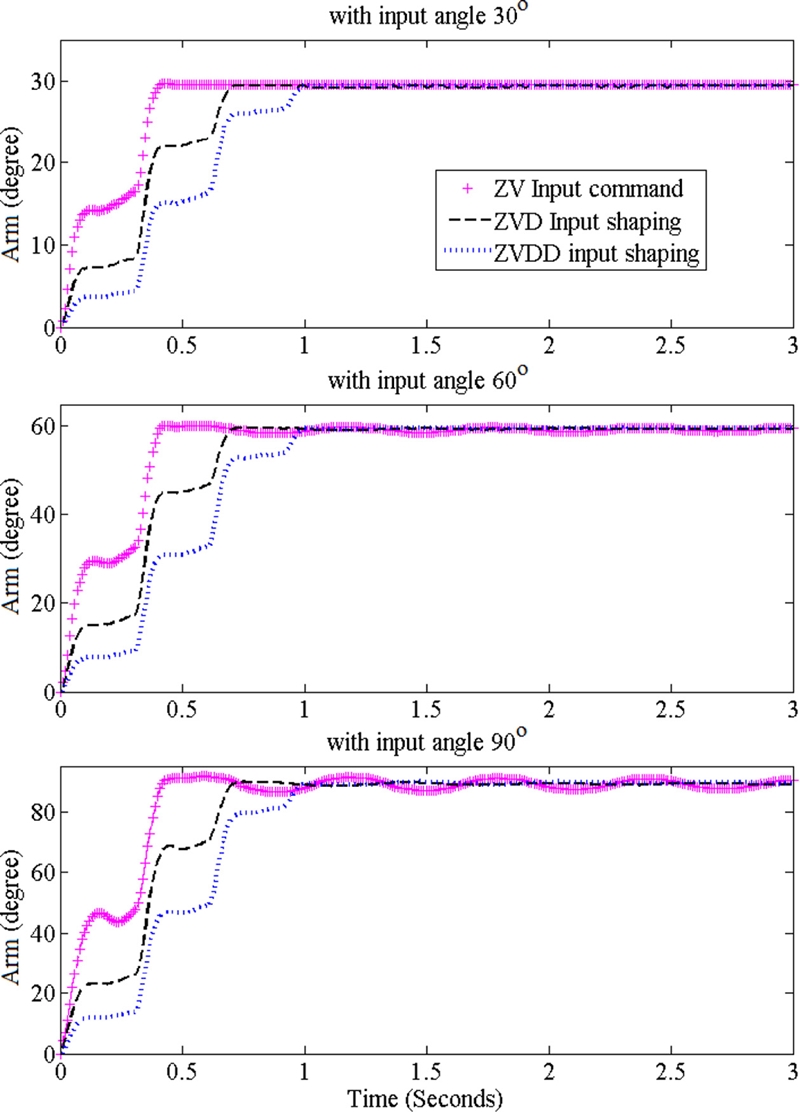
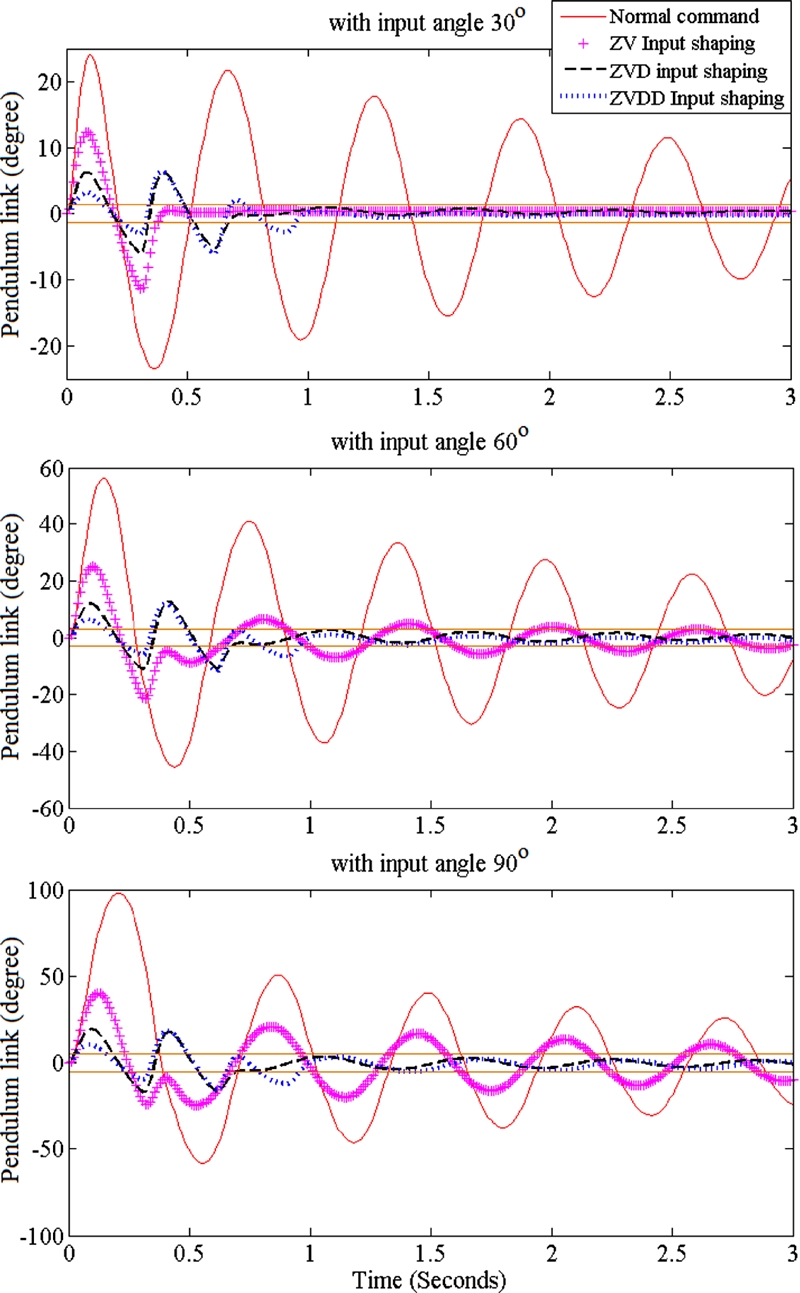
Resulting vibrations of both the arm and the pendulum link with the shaped inputs are shown in
Figs. 8 and
9, individually. The oscillation of the arm for 30
o reference arm angle disappears with any kind of input shapers, whereas ZVD and ZVDD are more effective than ZV for the motor reference angles of 60 and 90
o. The results of the pendulum link are even clearer, as shown from
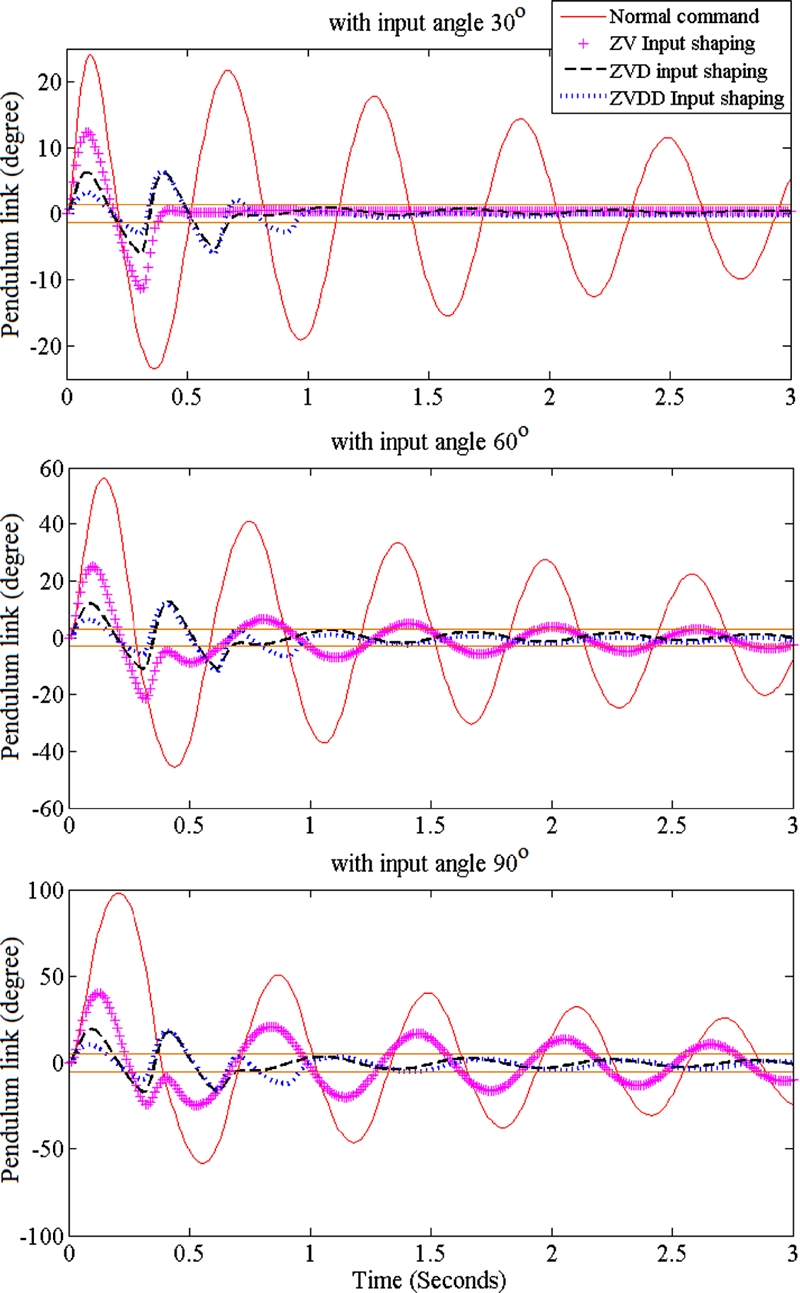
Fig. 7. The vibrations of the pendulum link are reduced dramatically with the input shapers. However, the ZV shaper has significant performance degradation compared with the ZVD and ZVDD shapers as the motor reference command increases and nonlinearity becomes severe.
Fig. 8Angular motions of the arm with various input shapers and reference arm angles
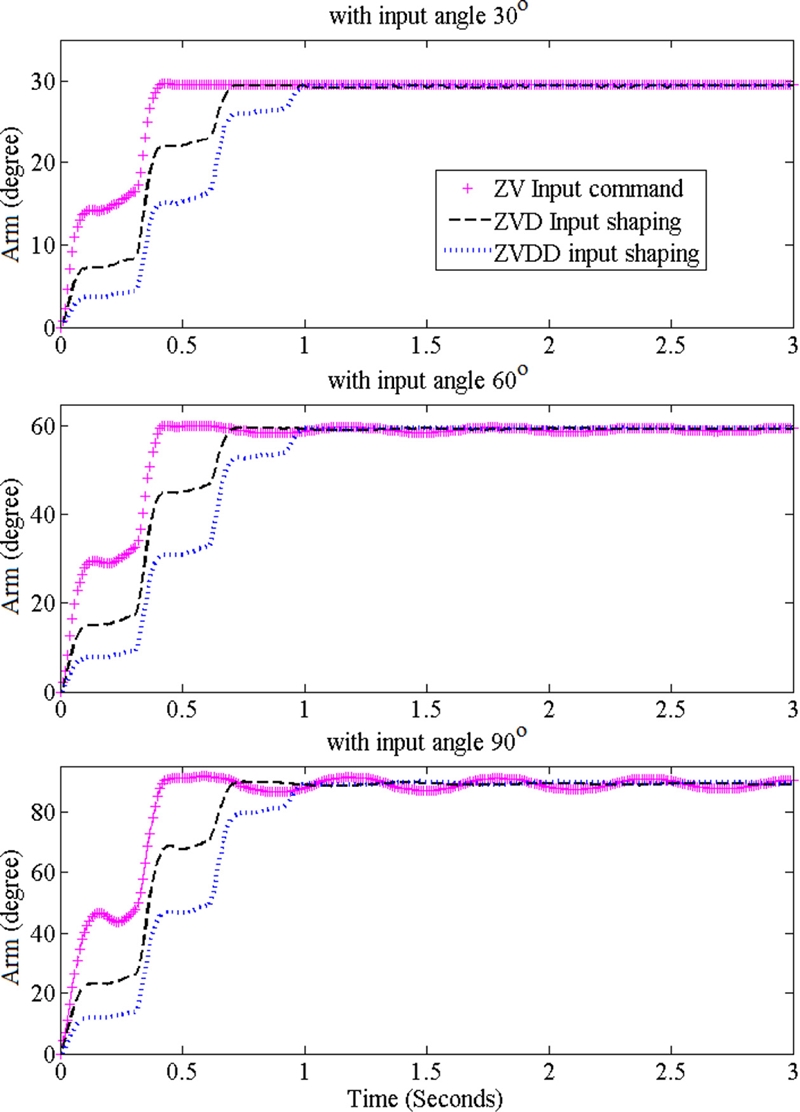
Fig. 9Vibrations of the pendulum link with various input shapers and reference arm angles
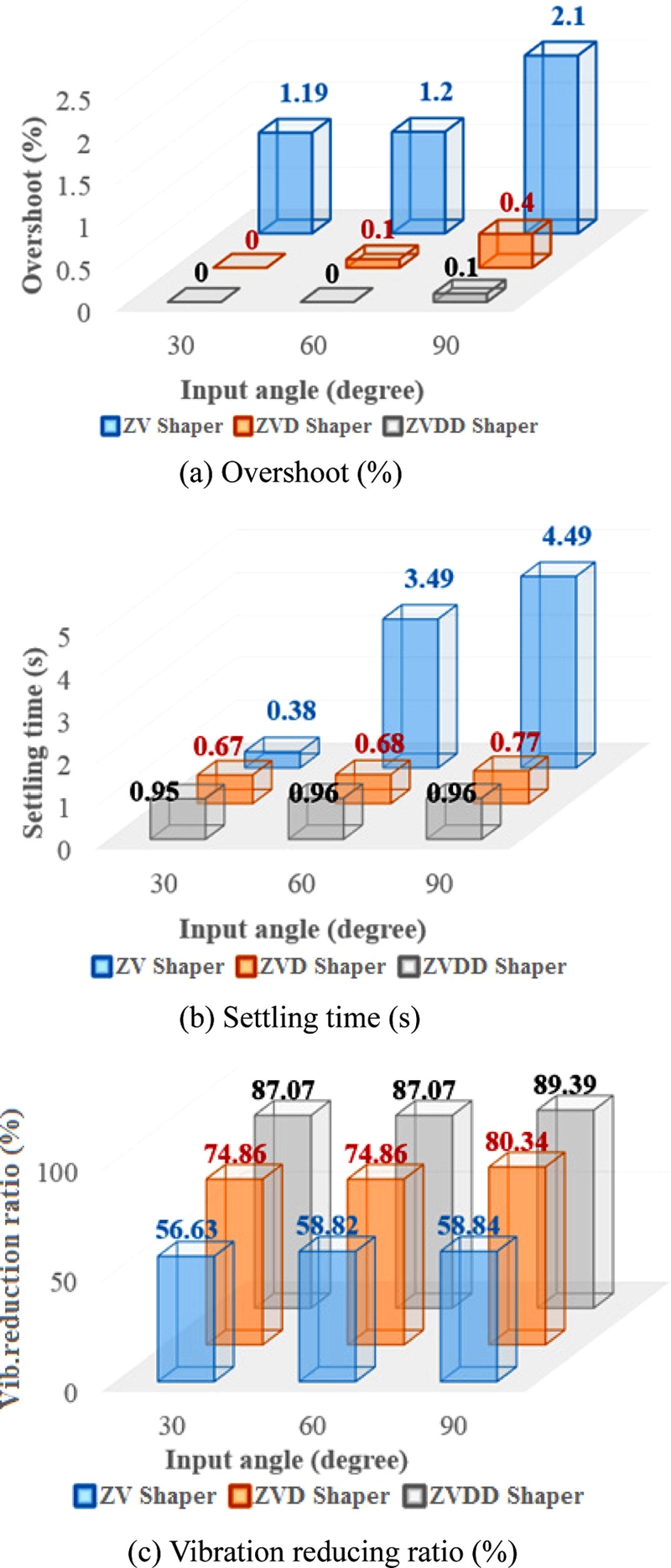
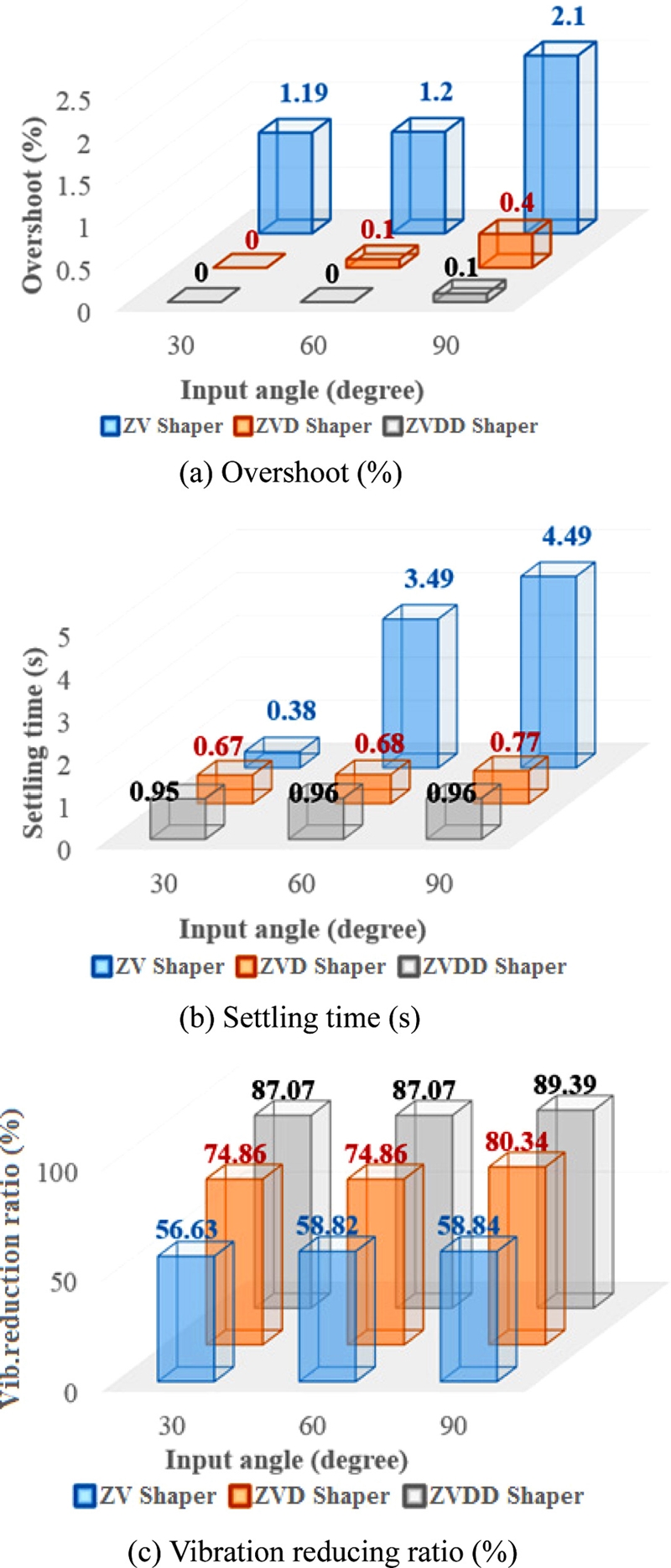
Overshot, settling time and vibration-reduction ratio of the Furuta pendulum are evaluated and shown in
Fig. 10. For the small reference arm angles (≤ 30
o), all shapers show similar performances. However, ZVD and ZVDD shapers show a better performance of not only shorter settling time (≤ 1 s) and overshoot (≤ 0.5%) but also larger vibration-reduction ratio (≥ 75%) as the motor reference angle increases and nonlinearity becomes critical. The ZV shaper cannot effectively deal with parameter variations of the nonlinear vibration caused by large reference command.
Fig. 10Performance evaluation of various input shapers
4. Conclusion
This paper presents the evaluation of input shaping methods for the nonlinear vibration system using a Furuta pendulum. First, the mathematical model of the Furuta pendulum is introduced and its nonlinear vibration characteristic is analyzed. Then, reference commands for cancelling the vibration of the Furuta pendulum are generated with various input shapers such as ZV, ZVD and ZVDD. Finally, we illustrate the effects of input-shaping methods on the Furuta pendulum by comparing the pendulum overshoot, settling time and vibration reduction ratio. The Furuta pendulum is proved to be a good motion platform to evaluate input shaping methods for nonlinear vibration system.
ACKNOWLEDGMENTS
This work was supported by The University of Danang, University of Science and Technology (No. T2020-02-03).
REFERENCES
- 1.
Fuller, C. C., Elliott, S., and Nelson, P. A., “Active Control of Vibration,” Academic Press, 1996.
10.1016/B978-012269440-0/50007-8
- 2.
Alkhatib, R. and Golnaraghi, M., “Active Structural Vibration Control: A Review,” Shock and Vibration Digest, Vol. 35, No. 5, pp. 367-383, 2003.
10.1177/05831024030355002
- 3.
Lu, Z., Wang, Z., Zhou, Y., and Lu, X., “Nonlinear Dissipative Devices in Structural Vibration Control: A Review,” Journal of Sound and Vibration, Vol. 423, No. 9, pp. 18-49, 2018.
10.1016/j.jsv.2018.02.052
- 4.
Yoo, S. J. and Ahn, H. J., “Software-Based Integral Product Architecture for Modular Motion Control System of a RFC Linear Motor Motion Stage: Model-Based DOB for Residual Vibration Suppression,” International Journal of Precision Engineering and Manufacturing, Vol. 21, No. 2, pp. 203-209, 2020.
10.1007/s12541-019-00212-y
- 5.
Li, L., Song, G., and Ou, J., “Nonlinear Structural Vibration Suppression Using Dynamic Neural Network Observer and Adaptive Fuzzy Sliding Mode Control,” Journal of Vibration and Control, Vol. 16, No. 10, pp. 1503-1526, 2010.
10.1177/1077546309103284
- 6.
Correa, J. C., “Parameter Identification and Monitoring of Mechanical Systems under Nonlinear Vibration,” Woodhead Publishing, pp. 35-53, 2014.
10.1533/9781782421665.35
- 7.
Srinivasan, P., “Nonlinear Mechanical Vibrations,” Wiley, 1st Ed., 1996.
- 8.
Wagg, D. and Neild, S., “Nonlinear Vibration with Control,” Springer International Publishing Switzerland, 2016.
- 9.
Singhose, W., “Command Shaping for Flexible Systems: A Review of the First 50 Years,” International Journal of Precision Engineering and Manufacturing, Vol. 10, No. 4, pp. 153-168, 2009.
10.1007/s12541-009-0084-2
- 10.
Tuttle, T. D. and Seering, W. P., “Experimental Verification of Vibration Reduction in Flexible Spacecraft Using Input Shaping,” Journal of Guidance, Control, and Dynamics, Vol. 20, No. 4, pp. 658-664, 1997.
10.2514/2.4128
- 11.
Maghsoudi, M. J., Mohamed, Z., Sudin, S., Buyamin, S., Jaafar, H., et al., “An Improved Input Shaping Design for an Efficient Sway Control of a Nonlinear 3D Overhead Crane with Friction,” Mechanical Systems and Signal Processing, Vol. 92, pp. 364-378, 2017.
10.1016/j.ymssp.2017.01.036
- 12.
Kim, B. G. and Hong, S. W., “Input Shaper Design for Tower Crane in Consideration of Nonlinear Coupled Motions,” Journal of the Korean Society for Precision Engineering, Vol. 26, No. 9, pp. 88-95, 2009.
- 13.
Kim, D. H., Sung, Y. G., and Jang, W. S., “Learning Input Shaping Control with Parameter Estimation for Nonlinear Actuators,” Transactions of the Korean Society of Mechanical Engineers A, Vol. 35, No. 11, pp. 1423-1428, 2011.
10.3795/KSME-A.2011.35.11.1423
- 14.
Hwang, K. J., Jeong, J. S., and Ahn, H. J., “Input-Shaping Methods for a Linear Motor Motion Stage with a Passive RFC (Reaction Force Compensation) Mechanism,” Journal of the Korean Society for Precision Engineering, Vol. 34, No. 12, pp. 897-902, 2017.
10.7736/KSPE.2017.34.12.897
- 15.
Furuta, K., Yamakita, M., and Kobayashi, S., “Swing-Up Control of Inverted Pendulum Using Pseudo-State Feedback,” Proceedings of the Institution of Mechanical Engineers, Part I: Journal of Systems and Control Engineering, Vol. 206, No. 4, pp. 263-269, 1992.
10.1243/PIME_PROC_1992_206_341_02
- 16.
La Hera, P. X., Freidovich, L. B., Shiriaev, A. S., and Mettin, U., “New Approach for Swinging Up the Furuta Pendulum: Theory and Experiments,” Mechatronics, Vol. 19, No. 8, pp. 1240-1250, 2009.
10.1016/j.mechatronics.2009.07.005
- 17.
Aguilar-Avelar, C. and Moreno-Valenzuela, J., “A Composite Controller for Trajectory Tracking Applied to the Furuta Pendulum,” ISA Transactions, Vol. 57, pp. 286-294, 2015.
10.1016/j.isatra.2015.02.009
- 18.
Garćıa-Alarćon, O., Puga-Guzḿan, S., and Moreno-Valenzuela, J., “On Parameter Identification of the Furuta Pendulum,” Procedia Engineering, Vol. 35, pp. 77-84, 2012.
10.1016/j.proeng.2012.04.167
- 19.
Aracil, J., Acosta, J., and Gordillo, F., “A Nonlinear Hybrid Controller for Swinging-Up and Stabilizing the Furuta Pendulum,” Control Engineering Practice, Vol. 21, No. 8, pp. 989-993, 2013.
10.1016/j.conengprac.2013.04.001
- 20.
- 21.
- 22.
- 23.
Biography
- Anh-Duc Pham
Received a Ph.D. degree from Soongsil University, Korea in 2018. He was a research associate in the IMSLab-Soongsil University and is currently a researcher/lecturer at the Faculty of Mechanical Eng., University of Science and Technology- The University of Danang. Dr. Pham’s research interests are in the area of mechatronics, control & precision machine design, sustainable design &manufacturing, applications of Nanomaterials.
- Hyeong-Joon Ahn
Received B.S., M.S. and Ph.D. degrees from Seoul national university, Korea in 1995, 1997 and 2001, respectively. He was research associate in University of Virginia, 2002 and is currently a professor at School of Mechanical Eng., Soongsil University. Dr. Ahn’s research interests are in the area of mechatronics, sensors, actuators, control and precision machine design.