ABSTRACT
The relationship between the break-up of hypervelocity jets (> 4 km/s) and the decrease in penetration capability was addressed in this study. By applying a theoretical study, three cases were compared: when the jet was not broken, when there was a decrease in segment length after the jet was broken, and when the velocity gradient became zero after the jet was broken. The results showed that the decrease in penetration capability due to the break-up of the hypervelocity jet was due to the reduction in the length of the jet segments and the uniformity of the velocity after the breakup.
-
KEYWORDS: Hypervelocity jet, Penetration capability, Break-up of jet
-
KEYWORDS: 초고속 제트, 관통 능력, 제트 끊어짐
Nomenclature
Square Root of Density Ratio
Square Root of Density Ratio
Length Reduction Rate of Broken Jet
Velocity Reduction Rate of Broken Jet
1. 서론
성형작약탄두는 원통형 실린더 형태의 화약과 콘 형태의 금속 라이너를 결합한 구조로, 이로부터 형성된 초고속 제트는 수십 밀리미터에 이르는 철판을 관통할 수 있는 위력을 갖고 있다. 이는 중장갑을 장착한 전차와 같은 고위협 기동 무기 체계를 무력화하는 용도로 유용하게 활용되고 있다.
성형작약탄두의 침투 현상을 기술한 다양한 연구가 1940년대 이후로 지금까지 꾸준히 이어지고 있다. Birkhoff, et al.의 유체역학적 침투(Hydrodynamic Penetration) 이론은 수 km/s 이상의 초고속 제트(Hypervelocity Jet)가 표적에 충돌할 때, 그 충돌 지점에는 표적의 강도를 훨씬 초과하는(10 GPa 이상) 높은 압력이 발생하기 때문에 제트와 표적 재료의 거동을 유체의 흐름으로 가정한 유체역학적 침투 이론(Hydrodynamic Penetration Theory)을 제시하였다[
1]. Eichelberger [
2]와 Pack and Evans [
3]는 표적의 강도와 초고속 제트의 침투 현상에 대한 실험적 분석을 통하여 Birkhoff, et al.의 유체역학적 침투 이론을 표적의 강도의 영향을 고려할 수 있는 이론으로 발전시켰다. 초고속 제트의 불균일 속도 분포를 고려한 침투 이론이 Abrahamson and Goodier [
4]에 의해 제시되어 보다 일반적인 침투 현상을 분석할 수 있게 되었다.
이와 같은 침투 이론 외에도 수치해석을 이용한 연구를 통해 금속 표적은 물론 세라믹, 복합소재 및 콘크리트와 같은 다양한 소재의 표적을 대상으로 한 연구들과[
5-
9], 더 우수한 침투 능력 확보를 위한 라이너 설계 개선에 대한 연구들도 이루어졌다[
10,
11].
초고속 제트의 유체역학적 침투 이론의 유효성에 관하여, Gooch, et al.은 제트의 속도에 따라 침투 현상을 지배하는 인자가 제트와 표적의 밀도비(γ) 우위에서 표적 강도(
Y) 우위로 전환됨을 보였다[
12]. Kang [
13,
14] 및 Kang and Sin [
15]은 유한요소해석 및 초고속 관통이론의 변형을 통해 유체역학적 침투 이론에 상응하는 제트의 침투 특성 및 침투 이론의 적용 범위에 대하여 연구하였다.
이와 같은 많은 연구를 통해 길고 빠른 초고속 제트일수록 침투 능력이 우수하다고 알려져 있다. 일반적으로 제트의 속도는 선두에서 가장 빠르며 후방에 이를 수록 느린 속도 구배를 갖는다. 이 속도 구배에 의해 표적까지 이동하는 동안 제트는 연장되는데, 과도한 연장은 제트의 끊어짐(Break-Up)을 초래하며 끊어진 제트의 침투 능력은 이전에 비해 감소한다고 받아들여지고 있다. 따라서, 끊어짐을 지연시키는 것이 더 큰 침투 능력 확보에 유리하다. Chou and Carleone은 제트의 항복응력과 밀도의 비(
Y⁄ρ)가 제트의 끊어짐에 주는 영향에 대하여
Y⁄ρ이 낮을 수록 끊어지는 시기가 늦어짐을 보였다[
16]. Carleone, et al.은 수치해석을 통해 제트의 넥킹(Necking)을 유발하는 임계파장(Critical Wavelength)은 연장률(Stretching Rate)와 관련되어 있음을 보였다[
17]. 그리고 Hirsch [
18,
19]는 끊어짐 발생 시간과 성형작약탄두의 형상 설계를 연계한 연구를 수행하였다. 이러한 연구에도 불구하고, 제트의 끊어짐은 당연히 침투 능력의 감소를 유발하는 것으로 받아들여지고 있는 경향이 크다.
이에 저자는 그 원인에 대한 명시적인 설명이 필요하다 판단하였고 이전의 이론을 적용하여 제트의 물리적 특성 변화와 침투 능력 사이의 영향성을 살펴보기로 하였다. 본 연구는 제트 끊어짐과 침투 능력 감소의 상관관계를 총 세 가지 경우로 구분하여 분석하였다. 먼저 Abramson and Goodier (A-G) 이론[
4]을 기반으로 끊어지지 않은 선형 속도 분포를 갖는 제트의 침투 능력을 분석하였다(경우 1). 다음으로 끊어짐을 고려할 수 있도록 A-G 이론을 변형하여 끊어진 제트 세그먼트의 길이 변화를 변수로 침투 특성을 분석하였다(경우 2). 마지막으로 끊어진 세그먼트의 길이도 감소되고 속도 구배 마저 사라진 후의 침투 능력을 Birkhoff, et al. [
1]을 이용하여 분석하였다(경우 3).
이를 통해 초고속 제트의 끊어짐에 인한 침투 능력 감소는 끊어짐 자체가 원인이기보다, 끊어진 후 제트 세그먼트들의 길이 감소 및 속도 구배 감소에 기인함을 보였다.
2. 접근방법
2.1 제트 세그먼트의 길이 변화 및 질량 보존
초기 상태(
t =
t0)에서 길이가
L0이며, 4 km/s 이상인 선형 속도 분포
v(
ζ)를 갖는 제트를 고려한다. 이 제트의 최대와 최소 속도는 각각
vmax와
vmin이며 각각 제트의 선단과 꼬리의 속도이다. 시간이 경과함에 따라(
ti) 불균일 속도 분포로 인해 제트의 길이는
Li로 연장된다. 이 과정 중 제트에 작용하는 항력 및 외력이 없고 끊어지지 않을 경우,
vmax 와
vmin 은 변화하지 않지만 제트 길이에 걸친 속도 구배는
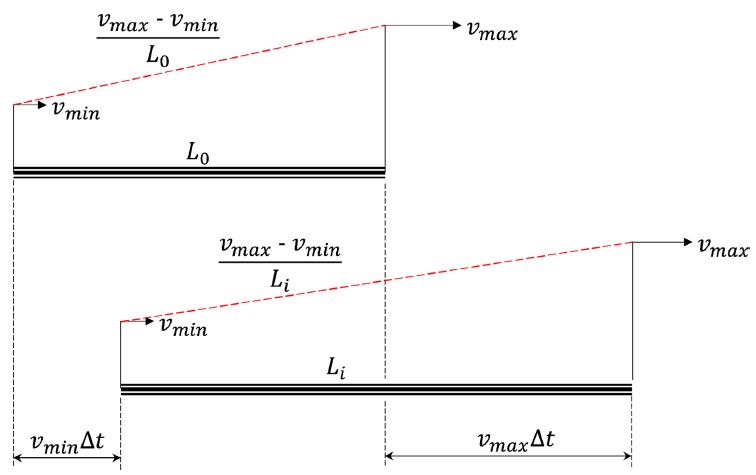
Fig. 1에 나타낸 것처럼 완만해진다.
Fig. 1Length and velocity gradient changes of a hypervelocity jet with time
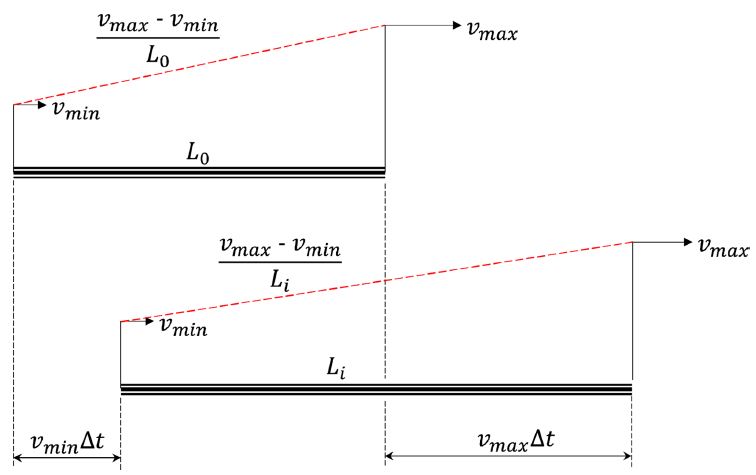
시간에 따른 제트 세그먼트의 길이 변화는 Δv = vmax-vmin, Δti = ti-1-ti, L-i=Li-L0 일 때, 다음과 같이 나타낼 수 있다.
제트가 표적에 충돌하기 전 소모되기 전의 질량은 일정하다고 하면 ρiVi = ρiVi–1이고, 이를 제트의 반지름과 길이를 통해 나타내면,
여기서 λ-i은 시간 t0로 부터 ti까지 제트의 연장률이다.
2.2 불균일 속도 분포를 갖는 초고속 제트의 침투 능력에 관한 이론적 배경
Abrahamson과 Goodier가 제안한 불균일 속도 분포를 갖는 제트의 침투 이론(A-G 이론)은 ‘전체 침투량’ P를 다음과 같이 기술한다.
여기서 ζ는 원점이 제트 세그먼트의 선단을 따라 이동하는 좌표계, S는 제트 선단과 표적의 표면 사이의 이격거리(Stand-Off)이다. 무차원 파라미터인 γ는 제트의 밀도(ρj)와 표적의 밀도(ρt) 비의 제곱근으로, γ=ρj/ρt이다. 제트의 속도 분포 v(ζ)가 길이에 따라서 선형적이라면 다음과 같이 나타낼 수 있다.
Kang and Shin은 선형적인 속도 분포를 갖는 제트에 대한 A-G 관통 이론의 다음과 같은 변형된 형태를 제시하였다.
여기서,
φl와
φs는 각각 제트 길이와 이격거리에 관련된 무차원 파라미터이다.
식(5.1)부터
식(5.3)과 같이 A-G 이론은 전체 침투량을 제트 길이와 이격거리에 대한 영향도로 구분하기 때문에 제트의 침투 능력을 선별적으로 검토하는데 유용하다.
식(5.1)부터
식(5.3)은 시간 변화에 관련된 항이 없기 때문에, 초기의 제트의 물리량(
L0,
S0)을 갖고 발생된 제트의 전체 침투량은 시간이 경과한 뒤 이 물리량들의 변화가 생긴 후에 계산된 결과와 동일하다. 따라서 시간이 지남에 따라 제트의 연장에 의해
Pl의 영향도는 증가하지만 이격거리의 감소로
Ps의 영향도는 감소하는 것을 알 수 있다. 시간(
ti,
i = 0, 1, 2, ..)이 경과함에 따라 제트 길의 변화가 전체 침투량에 주는 영향을 고려하면,
여기서 λi-1i는 시간 ti와 ti-1사이의 연장률, λ-i는 초기 시간 t0와 ti동안의 전체 연장률을 의미한다. 제트의 길이 연장을 일으키는 Δv=vmax-vmin이 양수이므로 λ-i 또한 양수이다. 따라서, Pl는 시간이 지남에 따라 전체 침투량에 더욱 큰 영향도를 갖게 된다.
반면에 이격거리의 변화가 전체 침투량에 차지하는 비율을 고려하면,
즉, 제트의 연장에 따라 이격거리는 감소되며 PS가 전체 침투량에 차지하는 영향도는 감소한다.
임의의 시간 ti에서의 전체 침투량은 Pl|ti와 Ps|ti의 합이다;
즉, vmax가 클수록 Pl과 Ps의 영향도는 증가할 수 있다. 하지만 본 연구에서는 vmin > 4 km/s으로 제한하였으므로 Ps의 영향도는 항상 Pl보다 낮을 수밖에 없다.
3. 끊어진 제트의 침투 특성
3.1 끊어진 제트 세그먼트에 대한 A-G 이론의 변형
초기 상태(t0)에서 선형적인 속도 분포 v(ζ)와 길이 L0를 갖는 제트가 시간 tb에 끊어질 경우의 침투 능력의 변화를 고려하고자 한다. 제트 선두에서 발생한 끊어짐이 전 영역으로 전파되는 과정의 상세한 과정을 단순화하여 제트의 전 영역이 길이가 동일한 n개의 세그먼트로 나누어졌다고 가정하면 각 세그먼트의 길이는 L0/n로 동일하다.
가장 선두에서부터
i번째 세그먼트의 이격거리는
Fig. 2와 같이 앞선 1-(
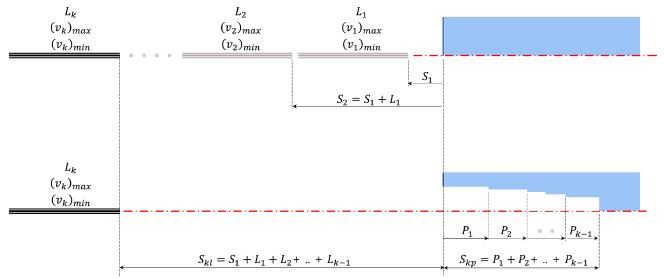
i-1)번째 세그먼트들의 길이의 합을 고려해야 함은 물론, 앞선 세그먼트들이 표적을 침투한 깊이의 합도 고려하여
식(11)로 나타낼 수 있다.
Fig. 2Stand-off distance of the k-th jet segment. (a) Consideration of length summation of previous jet segments, and (b) Consideration of partial penetration of previous jet segments
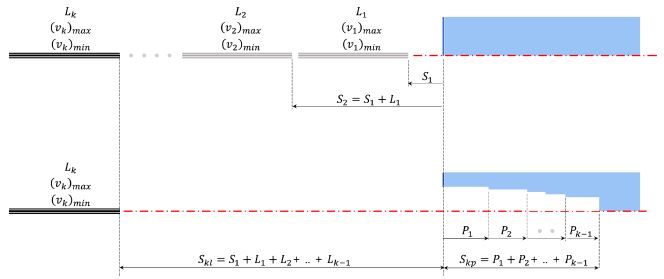
여기서, Lk와 Pk는 각각 i번째 세그먼트보다 앞선 k번째 세그먼트의 길이와 표적 침투량을 나타낸다.
각 세그먼트에 대하여
식(12)를 이용하여 침투량을 계산한 후 합하면 끊어진 제트의 총 침투량을 구할 수 있다.
끊어진 제트의 세그먼트는 길이와 속도 구배의 감소가 있을 수 있다. 끊어지기 직전까지 제트는 속도 구배에 의해 전방으로 연장되는데 이때 제트 내부에는 인장 응력이 발생된다. 이후, 생성된 세그먼트의 내부에는 이 응력이 이완되고 속도가 빠른 선두와 느린 꼬리는 세그먼트의 중심을 향해 가속 및 감속된다. 따라서 세그먼트의 길이는 끊어진 직후보다 짧아지고, 속도 구배는 적어진다[
20].
본연구는 세그먼트의 길이 감소율(ε)을 매개변수로 정하여 침투 특성의 변화를 분석하였다. 반면, 세그먼트의 속도 구배 감소율(θ)에 대하여는 매개변수로 설정하기보다는 속도 구배가 사라진 후의 침투 특성을 분석하였다.
3.2.1 경우 1–끊어지지 않은 제트의 총 침투량
L0가 100 mm이고,
vmax가 8 km/s로 일정한 대신
vmin이 4-8 km/s 범위 내에 있고,
S0는 0-100 mm 범위에 있는 제트를 고려한다. 이 제트의 재질은 OFHC (Oxygen Free High Carbon)이고 Steel 소재 표적을 침투한다고 가정하면 밀도비
γ는 1.06이다. 이 경우의 끊어지지 않은 제트의 총 침투량을
식(5)를 이용해 계산 결과를
Fig. 3과
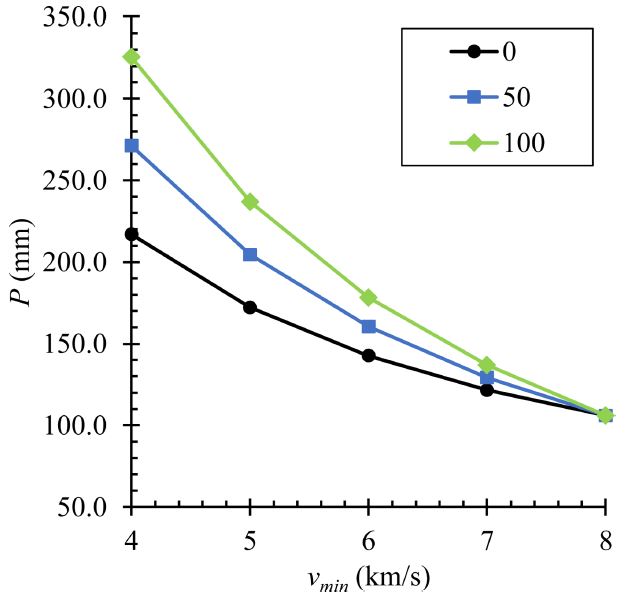
Table 1에 나타내었다.
Fig. 3Comparisons of total penetration amount with S0 and Δv variations in the case of the jet for not broken jet with vmax = 8 km⁄s
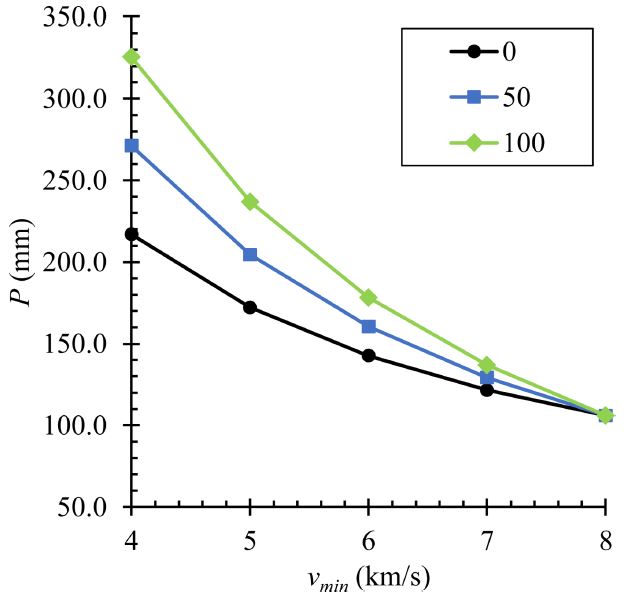
Table 1Comparisons of total penetration amount with S0 and Δv variations in the case of the jet for not broken jet with vmax = 8 km⁄s
Table 1
|
vmax = 8 km/s, not broken jet |
S0 [mm] |
|
0 |
50 |
100 |
|
vmin [km/s] |
4 |
217.0 |
271.2 |
325.5 |
|
5 |
172.2 |
204.5 |
236.8 |
|
6 |
142.6 |
160.4 |
178.3 |
|
7 |
121.6 |
129.2 |
136.8 |
|
8 |
106.0 |
106.0 |
106.0 |
S0가 멀고, Δv = vmax-vmin이 클수록 많은 침투량을 나타내었다. 반면, Δv가 적어질수록 S0에 무관하게 동일한 침투량 계산값으로 수렴하였다. 이는 Birkhoff, et al.의 침투 이론이 제트속도에 무관하게 초기 길이(L0) 와 밀도비(γ)만으로 침투량을 예측하는 것과 일치한다. 그리고 동일한 초기 길이와 밀도비를 갖는 경우일지라도 속도 구배가 큰 제트가 더 깊게 침투할 수 있음을 보여준다.
3.2.2 경우 2–끊어진 제트 세그먼트의 길이 변화가 발생한 경우의 총 침투량
제트가 끊어진 후 세그먼트 길이에 감소가 생긴 경우를 고찰하기 위해 초기 길이
L0 = 100 mm인 제트가
n = 40개의 균일한 길이를 갖는 세그먼트로 분할 되었다고 가정한다. 따라서 각 세그먼트의 길이는
L0/
n이며,
ε = 0 – 0.2까지 0.05씩 증가하도록 설정하여
식(12)를 이용해 계산하였다.
Tables 2(a)부터
2(e)에 이 계산 결과를 나타내었다. 전반적인 변화의 경향은
Fig. 3과 매우 유사하였다.
ε = 0인 경우를 나타내는
Table 2(a)의 결과는 정확하게 경우 1의 결과와 일치하였다. 이는 제트가 끊어지는 것 자체가 침투량 감소의 원인은 아님을 보여준다. 또한
식(5)와
식(12)가 길이 변화와 속도 변화가 없는 경우 서로 같은 결과를 도출함을 보임으로써
식(11)의 이격거리 계산이 타당함을 입증한 결과로 판단된다.
Tables 2(b)부터
2(e) 의 계산 결과를 비교해보면,
ε이 0.05씩 증가함에 따라 총 침투량은 감소함을 보였고 그 감소량은 Δ
v가 클수록 더 크게 감소하였다. 이는 큰 Δ
v는 더 깊은 침투를 할 수 있는 잠재성을 의미하지만, 길이 감소가 커질수록 상대적으로 더 많은 침투 능력을 상실함을 나타낸다.
Table 2Comparisons of total penetration amount with S0, Δv and ε variations in the case of broken jet
Table 2
(a) Broken jet,
ε = 0.00
vmax =8 km/s |
S0 [mm] |
|
0 |
50 |
100 |
|
vmin [km/s] |
4 |
217.0 |
271.2 |
325.5 |
|
5 |
172.2 |
204.5 |
236.8 |
|
6 |
142.6 |
160.4 |
178.3 |
|
7 |
121.6 |
129.2 |
136.8 |
|
8 |
106.0 |
106.0 |
106.0 |
(b) Broken jet,
ε = 0.05
vmax =8 km/s |
S0 [mm] |
|
0 |
50 |
100 |
|
vmin [km/s] |
4 |
206.1 |
260.44 |
314.6 |
|
5 |
163.6 |
195.9 |
228.2 |
|
6 |
135.5 |
153.3 |
171.1 |
|
7 |
115.6 |
123.2 |
130.8 |
|
8 |
100.7 |
100.7 |
100.7 |
(c) Broken jet,
ε = 0.10
vmax =8 km/s |
S0 [mm] |
|
0 |
50 |
100 |
|
vmin [km/s] |
4 |
195.3 |
249.5 |
303.8 |
|
5 |
155.0 |
187.3 |
219.6 |
|
6 |
128.4 |
146.2 |
164.0 |
|
7 |
109.5 |
117.1 |
124.7 |
|
8 |
95.4 |
95.4 |
95.4 |
(d) Broken jet,
ε = 0.15
vmax =8 km/s |
S0 [mm] |
|
0 |
50 |
100 |
|
vmin [km/s] |
4 |
184.4 |
238.7 |
292.9 |
|
5 |
146.4 |
178.7 |
210.9 |
|
6 |
121.2 |
139.1 |
156.9 |
|
7 |
103.4 |
111.0 |
118.6 |
|
8 |
90.1 |
90.1 |
90.1 |
(e) Broken jet,
ε = 0.15
vmax =8 km/s |
S0 [mm] |
|
0 |
50 |
100 |
|
vmin [km/s] |
4 |
173.6 |
227.8 |
282.1 |
|
5 |
137.8 |
170.1 |
202.3 |
|
6 |
114.1 |
131.9 |
149.8 |
|
7 |
97.3 |
104.9 |
112.5 |
|
8 |
84.8 |
84.8 |
84.8 |
3.2.3 경우 3–제트의 끊어짐이 일어나 세그먼트의 길이 변화 및 속도 구배가 사라진 경우의 총 침투량
본 절의 경우는 각 세그먼트들의 속도 구배가 사라진 경우로, Birkhoff, et al. [
1]의 이론을 이용하여 직관적으로 계산할 수 있다. 이전의 3.2.1절부터 3.2.2절을 참고하면 속도 구배가 없으므로 세그먼트의 길이 연장 효과도 사라진다. 따라서 속도 구배가 사라진 세그먼트들의 총 침투량은 길이 변화가 생긴 각 세그먼트를 일렬로 이은 하나의 제트의 침투량과 같으며 다음과 같이 나타낼 수 있다.
식(13)으로 계산된 결과는 경우
Tables 2(a)부터
2(e)의
vmin = 8 km/s 인 경우와 일치한다. 특히 매우 짧게 형성된 세그먼트의 경우, 각 세그먼트 내의 속도 차이는 무시할 수 있을 정도로 적어지므로 속도 차이와 길이와 같은 인자들이 침투량 증가에 불리한 방향으로 변화하게 됨을 유추할 수 있다.
4. 결론
본 연구는 끊어진 제트 세그먼트의 표적 침투 특성을 이론적인 접근을 통해 고찰하였다. 먼저, A-G 이론[
4]을 선형적인 속도 분포를 갖는 제트에 대한 식으로 변형하였다. 또한, 하나의 제트가 여러 세그먼트로 분할 되었을 때, 한 세그먼트의 표적침투량은 그 세그먼트의 표적 표면으로부터의 거리와 앞선 세그먼트들의 누적 침투량이 더해진 거리를 이격거리로 치환하여야 함을 보였다.
이러한 이론적 배경을 통하여 제트가 끊어지지 않은 경우 1, 제트가 끊어지면서 일정한 비율만큼 세그먼트의 길이가 짧아진 경우 2, 그리고 끊어진 제트의 길이가 극단적으로 짧아져 속도 구배가 사라진 경우 3과 같이 구분하여 총 침투량의 변화를 비교하였다.
이를 통해 제트가 끊어지는 경우 발생하는 표적 침투 능력 감소는 끊어짐 자체에 기인하기보다는 끊어진 후의 각 제트 세그먼트들의 길이 감소에 의한 것이 주요한 것으로 본 연구의 결과를 통해 예상할 수 있다.
다만 속도가 4 km/s 이상인 초고속 제트에 한정하여 연구가 이루어진 점, 실험을 통한 연구의 신뢰성 검증하지 못한 점이 이 연구의 실적용은 제한 사항을 갖는다. 하지만 실험 방법론을 확립하기에 앞서 이론적 고찰을 시도한 것은 의의가 있다고 판단된다. 이러한 연구는 향후 관련 분야의 연구에 있어, 제트의 끊어짐 이후에도 길이 수축이 적게 발생할 수 있는 라이너 재료의 선정 또는 제트 형성 메커니즘을 개발하는 연구에 기여할 것으로 기대된다.
REFERENCES
- 1.
Birkhoff, G., MacDougall, D. P., Pugh, E. M., Taylor, S. G., (1948), Explosives with lined cavities, Journal of Applied Physics, 19(6), 563-582.
10.1063/1.1698173
- 2.
Eichelberger, R. J., (1956), Experimental test of the theory of penetration by metallic jets, Journal of Applied Physics, 27(1), 63-68.
10.1063/1.1722198
- 3.
Pack, D., Evans, W., (1951), Penetration by high-velocity (Munroe’) jets: I, Proceedings of the Physical Society. Section B, 64(4), 298.
10.1088/0370-1301/64/4/302
- 4.
Abrahamson, G., Goodier, J., (1963), Penetration by shaped charge jets of nonuniform velocity, Journal of Applied Physics, 34(1), 195-199.
10.1063/1.1729065
- 5.
Cour-Palais, B. G., (1987), Hypervelocity impact in metals, glass and composites, International Journal of Impact Engineering, 5(1-4), 221-237.
10.1016/0734-743X(87)90040-6
- 6.
Bless, S., Rosenberg, Z., Yoon, B., (1987), Hypervelocity penetration of ceramics, International Journal of Impact Engineering, 5(1-4), 165-171.
10.1016/0734-743X(87)90036-4
- 7.
Zilberbrand, E., Vlasov, A., Cazamias, J., Bless, S., Kozhushko, A., (1999), Failure wave effects in hypervelocity penetration, International Journal of Impact Engineering, 23(1), 995-1001.
10.1016/S0734-743X(99)00142-6
- 8.
Dawson, A., Bless, S., Levinson, S., Pedersen, B., Satapathy, S., (2008), Hypervelocity penetration of concrete, International Journal of Impact Engineering, 35(12), 1484-1489.
10.1016/j.ijimpeng.2008.07.069
- 9.
Xue, L.-Z., Li, K.-Z., Jia, Y., Zhang, S.-Y., Ren, J.-J., You, Z.-Y., (2016), Effects of hypervelocity impact on ablation behavior of SiC coated C/C composites, Materials & Design, 108, 151-156.
10.1016/j.matdes.2016.06.106
- 10.
Kang, Y., Jeon, J., (2018), Finite element analysis of the impact of liner thickness and hydrodynamic limit on the penetration depth of a shaped charge warhead, Journal of Mechanical Science and Technology, 32(12), 5797-5805.
10.1007/s12206-018-1127-3
- 11.
Fedorov, S., Bayanova, Y. M., Ladov, S., (2015), Numerical analysis of the effect of the geometric parameters of a combined shaped-charge liner on the mass and velocity of explosively formed compact elements, Combustion, Explosion, and Shock Waves, 51(1), 130-142.
10.1134/S0010508215010141
- 12.
Gooch, W., Burkins, M., Walters, W., Kozhushko, A., Sinani, A., (2001), Target strength effect on penetration by shaped charge jets, International Journal of Impact Engineering, 26(1-10), 243-248.
10.1016/S0734-743X(01)00083-5
- 13.
Kang, Y., (2019), Finite element analysis for the penetration phenomena of shaped charge jets using hydrodynamic theory, Journal of the Computational Structural Engineering Institute of Korea, 32(2), 133-140.
10.7734/COSEIK.2019.32.2.133
- 14.
Kang, Y., (2019), A study on the strength irrelevance of hypervelocity penetration, Journal of the Computational Structural Engineering Institute of Korea, 32(3), 199-203.
10.7734/COSEIK.2019.32.3.199
- 15.
Kang, Y., Sin, H.-C., (2020), Effective velocity range of theoretical hypervelocity penetration models, Journal of Mechanical Science and Technology, 34(6), 2497-2506.
10.1007/s12206-020-0525-5
- 16.
Chou, P. C., Carleone, J., (1977), The stability of shaped-charge jets, Journal of Applied Physics, 48(10), 4187-4195.
10.1063/1.323456
- 17.
Carleone, J., Chou, P., Walters, W., Jameson, R., Ciccarelli, R., (1979), Prediction of shaped-charge jet breakup time and calculation of penetration (U), (Report No. ARBRL-CR-00396), US Army Ballistic Research Laboratories (BRL).
- 18.
Hirsch, E., (1981), A model explaining the rule for calculating the break-up time of homogeneous ductile metals, Propellants, Explosives, Pyrotechnics, 6(1), 11-14.
10.1002/prep.19810060104
- 19.
Hirsch, E., (1981), The natural spread and tumbling of the shaped charge jet segments, Propellants, Explosives, Pyrotechnics, 6(4), 104-111.
10.1002/prep.19810060406
- 20.
Biography
- Youngku Kang
CAE and System Engineer in Laser Division of Hanwha Co., Ltd.. He got his Ph. D. degree from the School of Aerospace and Mechanical Engineering of Seoul National University. He has been worked on the design of mechanical systems by using CAE based on the finite element analysis.