ABSTRACT
With advancements in semiconductor manufacturing processes and the development of precision processing technology, flexure hinge-based ultra-precision positioning stages are widely used. In the flexure hinge, axial and bending stiffness properties greatly influence positioning performance. This study examined the stiffness properties of elliptic and parabolic 2-degrees-of-freedom (DOF) hinges, which have not been extensively discussed. The Timoshenko beam theory was applied to derive the stiffness equations for the axial and bending directions of each hinge. The stiffness properties were examined in several design conditions by comparing theoretical and finite element analyses. Based on the results of the analyses, an empirical formula in exponential form for the design of an elliptic hinge was constructed through surface-fitting. The elliptic hinge was found to be a better alternative to a circular hinge under certain design conditions by adjusting two design parameters. In the future, we will develop sophisticatedly designed hinges with improved axial and bending stiffness properties compared to the existing circular and elliptic hinges.
-
KEYWORDS: Axial stiffness, Bending stiffness, Finite element analysis, Elliptic flexure hinge, Parabolic flexure hinge
-
KEYWORDS: 축방향 강성, 굽힘방향 강성, 유한요소해석, 타원형 플렉셔 힌지, 포물선형 플렉셔 힌지
1. 서론
구동기에 의해 발생된 움직임을 링크 간의 상태운동을 통해 전달하여 최종적인 운동을 만들어 내는 기존 방식의 위치 결정 스테이지에서는 유격, 마찰, 마모, 비산물 발생 등의 문제점이 존재한다. 반도체 공정, 나노 공학에서의 나노 구조물 측정, 나노 가공 등의 분야에서는 서브 나노급의 분해능과 높은 정밀도, 비산물 없는 클린룸 호환 가능성 등의 필요가 있어서 새로운 방식의 위치 결정 스테이지를 필요로 한다. 링크 간의 조립 및 상대운동 없이 힌지의 변형만으로 구동기의 움직임을 전달하는 위치 결정 스테이지가 이러한 분야에서의 대안으로 개발되어 널리 활용되고 있다
[1,
2].
플렉셔 힌지 기반의 위치 결정 스테이지에 대한 연구가 다수 진행되어 왔으나, 주로 운동을 전달 및 증폭하기 위한 구조와 성능 최적화, 제어 내용에 대한 것이다. 플렉셔 힌지 자체의 설계 및 해석에 대해 다룬 연구도 존재하지만 대부분 1 자유도운동을 구현하기 위한 원형 단방향 플렉셔 힌지에 대한 것이다. 평면상의 운동은 1 자유도 힌지로 구현이 가능하지만, 공간상의 운동은 2 자유도 힌지를 필요로 한다
[3,
4]. 또한, 원형 플렉셔 힌지가 설계, 가공, 넓은 영역에 걸친 활용성 등의 측면에서 유리하지만 위치 결정 스테이지의 사용 목적에 따라 다른 형태의 플렉셔 힌지를 고려하는 것도 필요하다. 효율적으로 위치 결정 성능을 구현하기 위해서는 먼저 적합한 형태의 플렉셔 힌지를 선택하고 관련 설계 변수에 따른 축방향(Axial Stiffness) 및 굽힘방향(Bending Stiffness) 강성의 변화를 예측할 수 있어야 한다
[5,
6].
본 연구를 통해 공간적 움직임 구현에 활용할 수 있는 2 자유도 타원형, 포물선형 플렉셔 힌지에 대한 이론식 수립 및 강성 계산, 유한요소해석을 통한 성능 비교, 설계 변수에 따른 강성 특성에 대해 고찰한다. 특히, 원형 플렉셔 힌지 적용을 제한하는 설계 조건에서의 타원형, 포물선형 플렉셔 힌지의 활용 가능성에 대해 살펴보고자 한다. 또한, 유한요소해석 결과를 기초로 강성 실험식을 도출하여 타원형 및 포물선형 플렉셔 힌지 설계에 활용할 수 있도록 제시하고자 한다.
본 논문은 다음과 같이 구성 되어 있다. 1장에서는 연구의 배경 및 필요성을 기술한다. 2장에서는 티모셴코 빔 이론을 바탕으로 타원형 플렉셔 힌지와 포물선형 플렉셔 힌지의 강성에 대한 이론식을 수립한다. 3장에서는 이론식과 유한요소해석 결과를 비교하고 설계 변수 변화에 따른 각 힌지의 특성을 고찰한다. 또한, 타원형 플렉셔 힌지와 포물선형 플렉셔 힌지의 설계 및 적용상의 유의점에 대해 논의한다. 4장에서는 플렉셔 힌지 설계과정에서 강성 예측에 활용할 수 있도록 이론식과 유한요소해석 결과를 바탕으로 지수함수 형태의 실험식을 고안한다. 5장에서는 연구의 결론을 제시한다.
2. 2 자유도 타원형, 포물선형 플렉셔 힌지의 강성 해석
서브 마이크로미터 단위의 구동을 하는 초정밀 위치 결정 스테이지에서 플렉셔 힌지는 필수 구성요소이다. 위치 결정 스테이지에서 사용되고 있는 단방향 플렉셔 힌지는 낮은 강성을 갖는 1개의 회전 자유도와 높은 강성을 갖는 5개의 자유도로 인해 조인트와 같은 역할을 하게 된다.
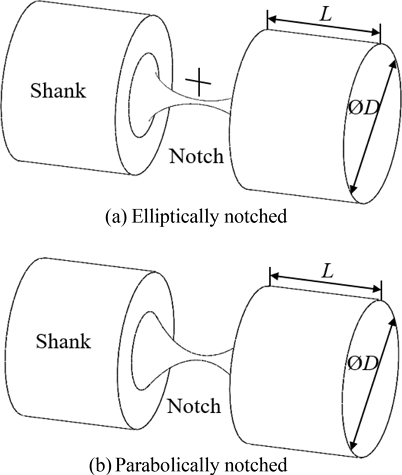
2 자유도 플렉셔 힌지가 필요한 이유는 1개의 힌지가 2개의 회전 자유도가 가져야, 3자유도를 초과하는 이송 자유도를 갖는 위치 결정 스테이지에서 평면을 벗어난 공간적 움직임의 구현이 가능하기 때문이다. 이와 같은 플렉셔 힌지를 2 자유도 플렉셔 힌지(2-DOF Flexure Hinge)라고 하며 그 중 타원형 노치(Notch)와 포물선형 노치를 갖는 2 자유도 플렉셔 힌지의 형상을
Fig. 1에 나타내었다
[7].
Fig. 1 Cylindrical flexure hinges
2 자유도 플렉셔 힌지는 대칭적인 구조를 가지고 있으며, 축방향은 강성이 높고 굽힘에 의한 회전방향은 강성이 낮아야 조인트와 같은 기능을 적절히 수행할 수 있다. 따라서 2 자유도 플렉셔 힌지는 응력이 허락하는 한도 내에서 2개의 회전자유도의 강성은 낮게, 축방향의 강성은 높게 설계하는 것이 바람직하다.
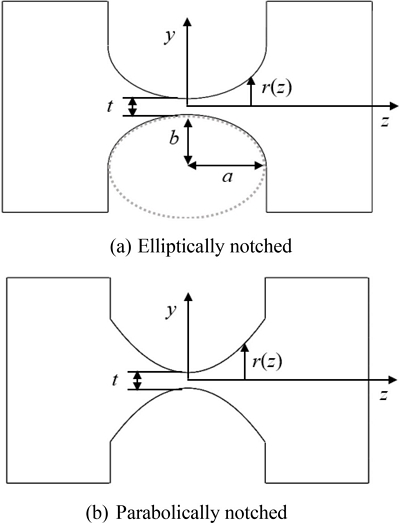
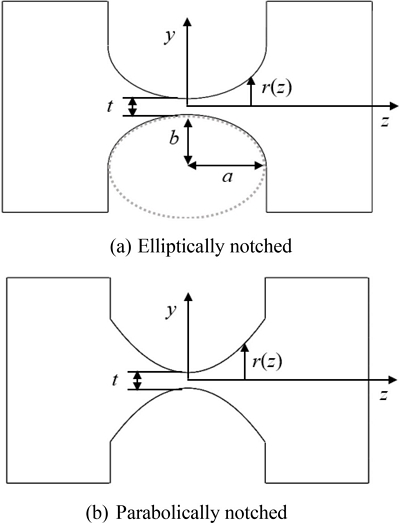
2 자유도 플렉셔 힌지의 대칭성으로 인해 축방향과 굽힘방향으로 성질이 분리가 된다.
Fig. 2와 같이 축방향을
z축이라고 할 때
x축과
y축 방향의 특성은 같고
z축 방향은 다르다. 따라서
x축과
y축 방향의 회전 강성을 굽힘방향 강성
Kb라고 하고,
z축 방향의 강성을 축방향 강성
Ka라고 한다. 이를 식으로 나타내면 다음과 같다.
Fig. 2 Cutaway views of the cylindrical flexure hinges
위와 같은 강성은 다음의 두 식을 기본으로 한다.
여기에서
i는
x,
y,
z와 같은 좌표축이고,
δ와
θ는 각각 변형 길이와 변형각을 의미하며,
F와
M은 각각 힘과 모멘트를 의미한다. 2 자유도 플렉셔 힌지의 단면 형상이 타원과 포물선 형태 각각에 대해
Fig. 2에 나타나 있다.
티모셴코 빔 이론에 따라 응력-변형률 공식과 인장 및 굽힘에 관한 공식들을 활용하여 플렉셔 힌지 설계에 가장 중요한 역할을 하는 축방향 강성
Ka와 굽힘방향 강성
Kb를 다음과 같이 계산할 수 있다
[8-
10].
여기에서 E는 탄성계수, G는 전단탄성계수, A는 단면적, I는 관성모멘트, Iz는 극관성모멘트를 각각 의미한다. z축에 직각인 단면의 단면적과 관성 모멘트와 극관성 모멘트는 각각 다음과 같다.
힌지의 축방향인
z축에 직각인 단면의 반경
r은, 노치의 형상이 타원과 포물선일 경우에 각각 다음과 같다(
Fig. 2 참조).
여기에서
a는 타원형 플렉셔 힌지의 횡반경(Transverse Radius)을,
b는 종반경(Longitudinal Radius)을 나타내고
p는 포물선형 플렉셔 힌지의 이차항 계수를 나타낸다.
식(7)부터
식(11)을
식(5)와
식(6)에 대입하여 축방향 강성
Ka와 굽힘방향 강성
Kb를 계산하였으며, 그 결과는 지면의 한계가 있어서
부록에 수록하였다.
3. 유한요소해석과 이론식 결과 비교
3.1 설계변수와 하중 및 경계 조건
2 자유도 플렉셔 힌지의 설계변수는 노치에서 가장 가는 부분의 지름 t와 타원형의 경우 장반경, 단반경(여기에서는 알기 쉽게 횡반경 a, 종반경 b라고 함)이며 포물선형의 경우 이차항의 계수 p이다. 해석을 위해 설계한 힌지는 노치를 포함하여 전체 길이가 120 mm이다. 자루의 지름(D)은 41 mm로 선정하여 자루의 변형이 전체 해석 결과에 영향을 주지 않도록 노치 지름 대비 충분히 큰 값으로 정하였다. 노치 지름 t는 1 mm로 고정하였고 노치 길이의 경우 타원형 플렉셔 힌지에서는 횡반경(a = 10 mm) 또는 종반경(b = 10 mm)을 고정하고 나머지 변수를 2.5, 5, 10, 20, 40 mm로 정했다. 그러므로 종반경을 고정한 경우의 노치 길이는 횡반경의 2배(5, 10, 20, 40, 80 mm)가 된다. 포물선형 플렉셔 힌지의 이차항 계수 p는 0.025, 0.05, 0.1, 0.2, 0.4로 정했으며, 이에 따라 노치 길이는 10, 14.1, 40, 56.6, 80 mm가 된다.
하중 조건(F, M)은 힌지의 중심 곧 노치의 가장 가는 부분의 허용응력이 재료의 항복응력에 안전계수 2를 적용한 값을 만족하도록 정했다. 재료는 위치 결정 스테이지의 플렉셔 힌지로 널리 사용되고 있는 AL7075-T6 를 적용했으므로 허용응력은 재료 항복응력(493.8 MPa)의 절반인 246.9 MPa이 된다.
유한요소해석을 위해 자루(Shank) 끝 부분을 고정시키고 반대편 끝 부분에 모멘트(M = 24.24 Nmm)를 부가하였다. 격자는 힌지 중심의 격자가 t 대비 작게 생성하였고, 타원형 플렉셔 힌지의 한 가지 설계조건(a = 10 mm, b = 20 mm인 경우)에 대해 격자수는 29,703개, 노드수는 48,657 개가 생성됨을 확인하였다.
3.2 이론식과 유한요소해석 결과
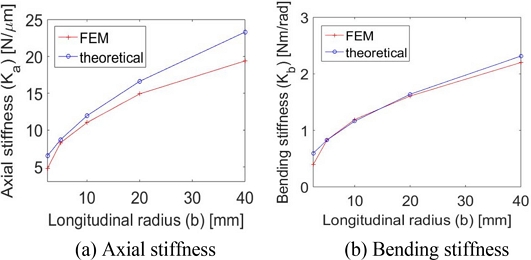
타원형 플렉셔 힌지의 주된 설계 변수인 횡반경
a와 종반경
b에 따른 축방향 강성
Ka와 굽힘방향 강성
Kb의 변화를
Fig. 3에 그래프로 나타내었다.
Fig. 3은 횡반경을 고정하고 종반경을 변화시킨 결과를 축방향 강성과 굽힘방향 강성으로 나누어 표현한 것이다. 유한요소해석과 이론식 결과값은 구간에 따라 오차가 존재하지만 전체적으로 유사한 경향을 나타내었다. 유한요소해석 결과가 이론식에 비해 낮은 이유는 티모셴코 빔 이론에서 힌지 각 단면에서의 응력 분포가 동일하다는 가정이 있지만, 실제로는 힌지 중심부와 표면의 응력 분포가 불균일하기 때문인 것으로 판단된다. 특히, 노치부의 형상 변화가 급격할수록 힌지 내부 응력 분포가 불균일해져서 오차가 크게 발생하게 된다.
Fig. 3Stiffness comparison between FEM and theoretical analyses for elliptic hinge with fixed transverse radius a (= 10 mm)
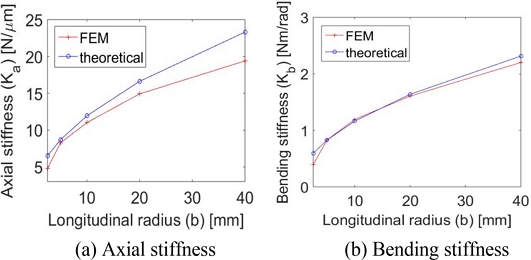
Table 1Stiffnesses resulted from theoretical calculation and finite element analysis for elliptic hinge with fixed transverse radius a (= 10 mm)
Table 1
|
b [mm] |
2.5 |
5 |
10 |
20 |
40 |
|
Theoretical |
Ka [N/um] |
6.5 |
8.7 |
11.9 |
16.6 |
23.3 |
|
Kb [Nm/rad] |
0.6 |
0.8 |
1.2 |
1.6 |
2.3 |
|
FEM |
Ka [N/um] |
4.7 |
8.3 |
11.0 |
14.9 |
19.4 |
|
Kb [Nm/rad] |
0.4 |
0.8 |
1.2 |
1.6 |
2.2 |
모든 설계 조건에서 노치부 중심 지름인
t가 동일함에도 불구하고 중심부 주변의 지름 변화가 전체 힌지 강성에 영향을 주고 있음을 확인할 수 있다. 이 사실은 동일한
t값이라 하더라도 힌지의 형태를 원형, 타원형, 포물선형 등으로 변화시킬 때에 플렉셔 힌지의 강성을 변화시키는 설계가 가능함을 의미한다.
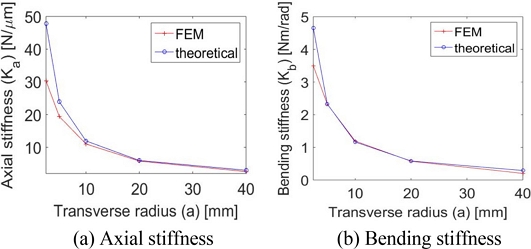
Fig. 4에서는 종반경을 고정하고 횡반경을 변화시켰을 때의 강성 변화를 보여준다.
Fig. 3과 반대로 횡반경이 커짐에 따라 축방향 및 굽힘 강성값이 모두 낮아지는 것을 확인할 수 있다.
Fig. 4Stiffness comparison between FEM and theoretical analyses for elliptic hinge with fixed longitudinal radius b (= 10 mm)
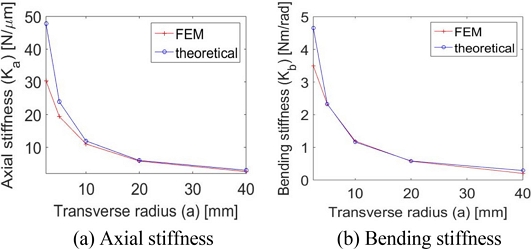
Table 2Stiffnesses resulted from theoretical calculation and finite element analysis for elliptic hinge with fixed longitudinal radius b (= 10 mm)
Table 2
|
a [mm] |
2.5 |
5 |
10 |
20 |
40 |
|
Theoretical |
Ka [N/um] |
47.8 |
23.9 |
11.9 |
6.0 |
3.0 |
|
Kb [Nm/rad] |
4.7 |
2.3 |
1.2 |
0.6 |
0.3 |
|
FEM |
Ka [N/um] |
30.3 |
19.4 |
11.0 |
5.8 |
2.6 |
|
Kb [Nm/rad] |
3.5 |
2.3 |
1.2 |
0.6 |
0.2 |
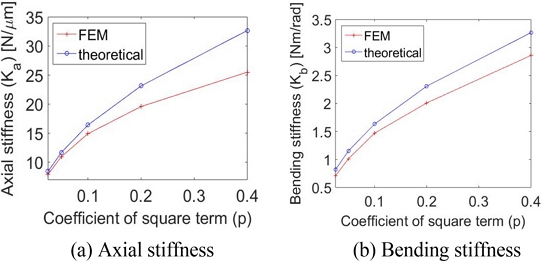
포물선형 플렉셔 힌지의 이차항의 계수인
p값의 변화에 따른 축방향 강성과 굽힘방향 강성값의 변화는
Fig. 5에 나타나 있다. 포물선형 플렉셔 힌지는 타원형 플렉셔 힌지와 달리 설계변수가 1개이므로 설계상으로는 원형 플렉셔 힌지와 차이점이 존재하지 않는다. 플렉셔 힌지는 일정한 축방향의 하중을 지지하면서도 조인트의 역할을 잘 수행하기 위해 굽힘방향 강성은 낮게, 축방향 강성은 크게 설계하는 것이 유리한데,
Fig. 5를 보면 포물선형 플렉셔 힌지는 원형 플렉셔 힌지(
Ka = 11.02 N/um,
Kb = 1.19 Nm/rad)에 비해 굽힘방향 강성이 낮은 설계 구간이 좁은 편이어서 원형 플렉셔 힌지 대비 설계상의 이점이 크게 보이지 않는다.
Fig. 5Stiffness comparison between FEM and theoretical analyses for parabolic hinge
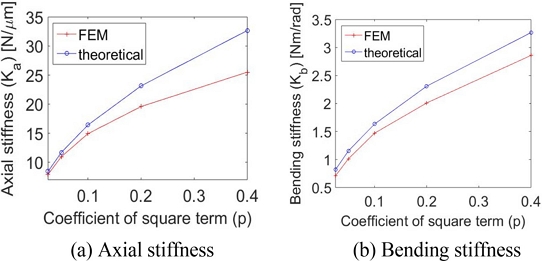
Table 3Stiffnesses resulted from theoretical calculation finite element analysis for parabolic hinge
Table 3
|
p |
0.025 |
0.05 |
0.1 |
0.2 |
0.4 |
|
Theoretical |
Ka [N/um] |
8.4 |
11.7 |
16.4 |
23.1 |
32.7 |
|
Kb [Nm/rad] |
0.8 |
1.2 |
1.6 |
2.3 |
3.3 |
|
FEM |
Ka [N/um] |
7.9 |
11.0 |
14.9 |
19.6 |
25.5 |
|
Kb [Nm/rad] |
0.7 |
1.0 |
1.5 |
2.0 |
2.9 |
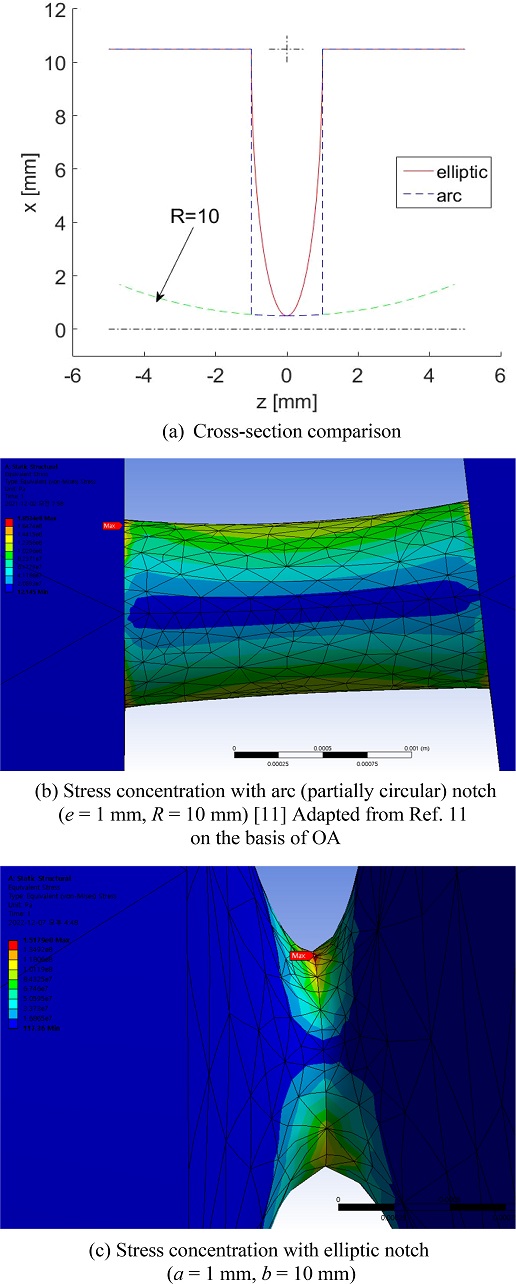
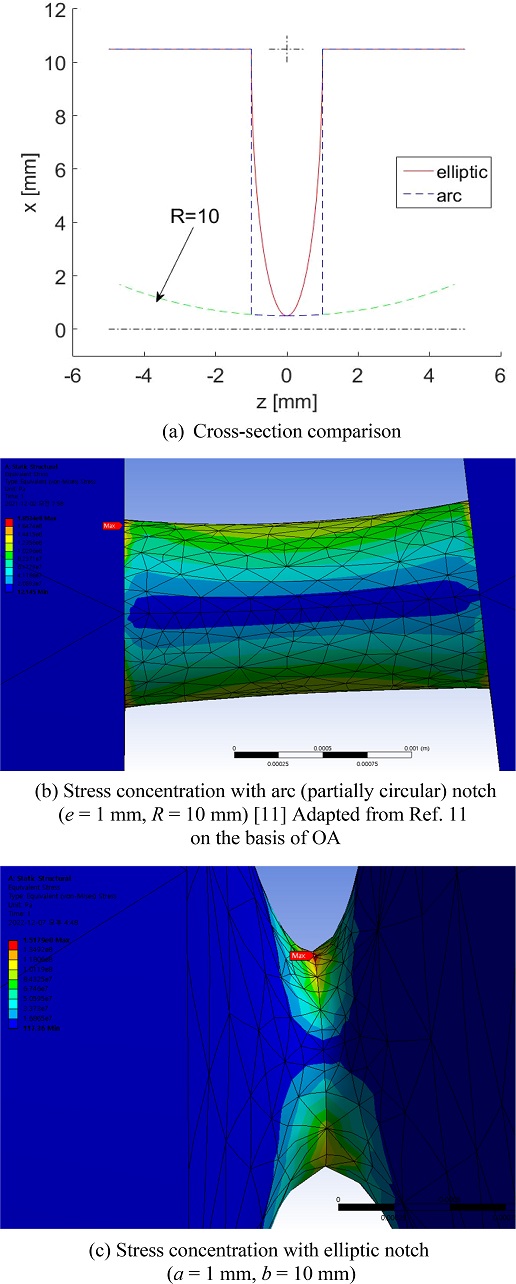
타원형 플렉셔 힌지의 활용에 있에서 주목할 점은 노치 부분과 자루가 접하는 부분에서 노치의 표면 기울기와 자루의 기울기를 일치시켜서 서로 접하게 설계함으로써 불필요한 응력 집중을 줄일 수 있다는 점이다. 원형 플렉셔 힌지의 경우 설계 변수가 1개이므로 노치 길이가 정해져 있는 경우 필요로 하는 반경을 지니면서도 노치와 자루가 서로 접하도록 설계하기가 불가능한 경우가 발생한다. 그러나 타원형 플렉셔 힌지는 2개의 설계 변수를 독립적으로 선정하여 설계할 수 있다. 그러므로 노치의 중심부에서 곡률반경은 원형 플렉셔 힌지와 동일하면서도 노치와 자루가 만나는 부분이 급격하게 형상이 변하지 않는 설계가 가능하다.
이는 노치와 자루가 만나는 부분의 응력이 과도하게 발생하지 않게 설계할 수 있도록 대안을 제시해 주는 것이다. 선행 연구
[11]에서 완전한 원이 아닌 호 형태의 노치일 때(
e = 1 mm,
R = 10 mm) 응력집중이 해당 논문의
Fig. 9에 나타나 있는 것과 같이 노치와 자루의 연결부위에서 발생하며 계산된 응력집중계수는 1.483이다. 하지만 이번 연구에서 노치의 길이가 같은 경우에 타원형(
a = 1 mm,
b = 10 mm)으로 적용하면 응력집중이 노치의 중앙부에서 발생하며 계산된 응력집중계수는 1.214이다. 단면 형상의 비교는
Fig. 6에 표시하였다.
Fig. 6Comparison between circular and elliptic notches
4. 곡선 보간 및 곡면 보간을 통한 실험식 구성
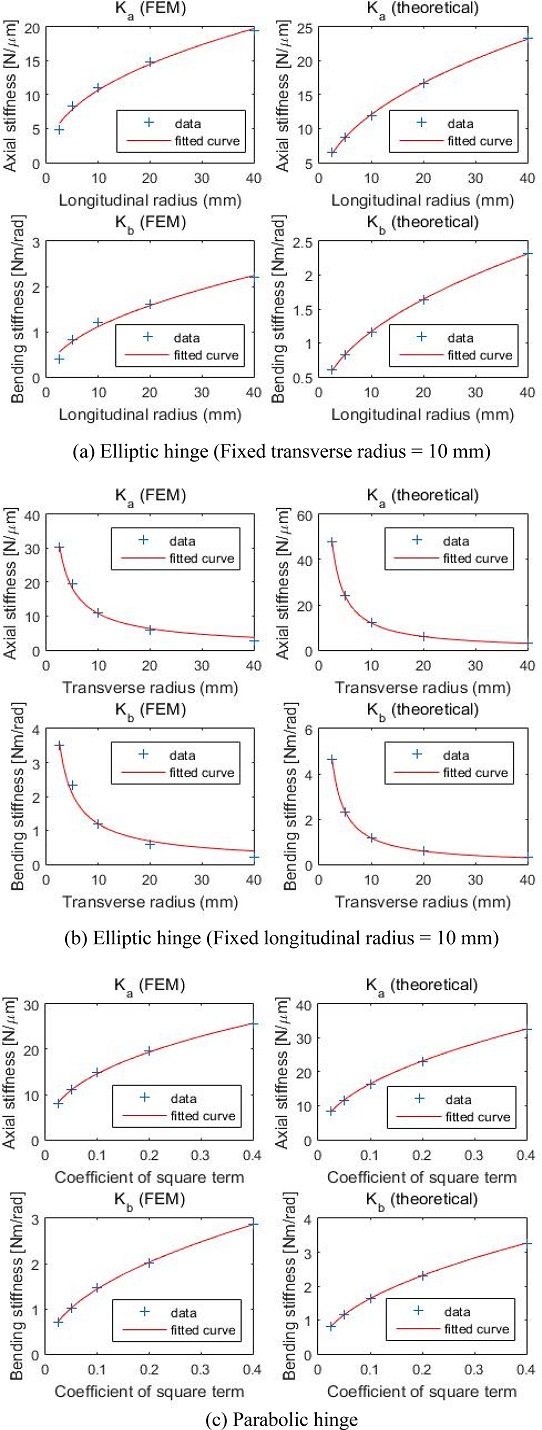
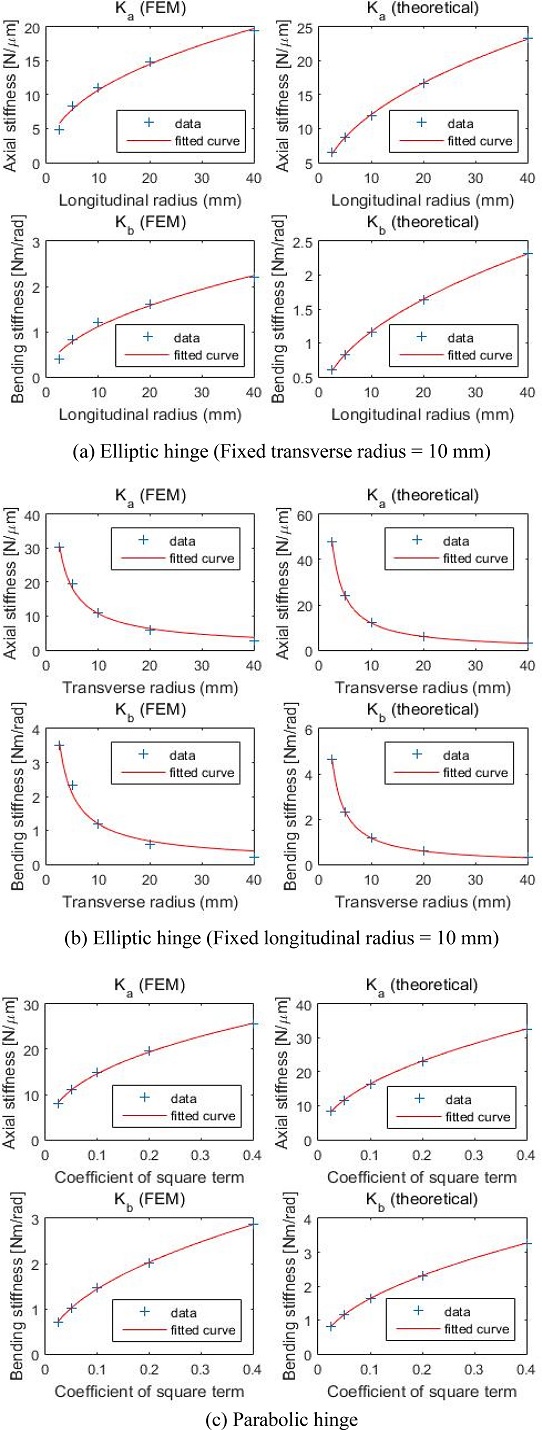
먼저 앞에서 수행한 이론 및 유한요소해석 결과를 바탕으로 곡선 보간을 수행하여
Fig. 7에 나타내었다. 타원형 플렉셔 힌지의 경우 한 가지 설계 변수를 고정한 상태에서 나머지 설계 변수가 변화함에 따라 축방향 및 굽힘방향 강성이 어떻게 변화하는지 예측하기에 용이하다. 또한 포물선형 플렉셔 힌지는 설계변수가 한 개이므로 곡선 보간을 통해서 각 강성값의 변화 경향을 예측할 수 있다.
Fig. 7 Curve fitting for FEM and theoretical calculation
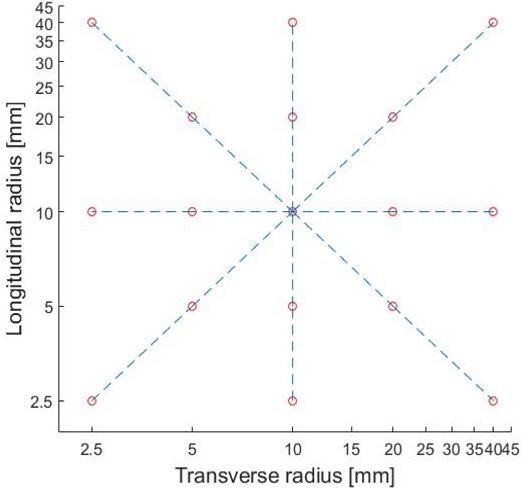
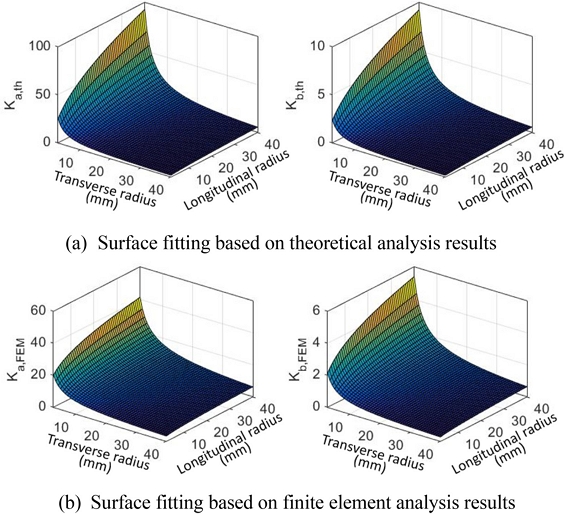
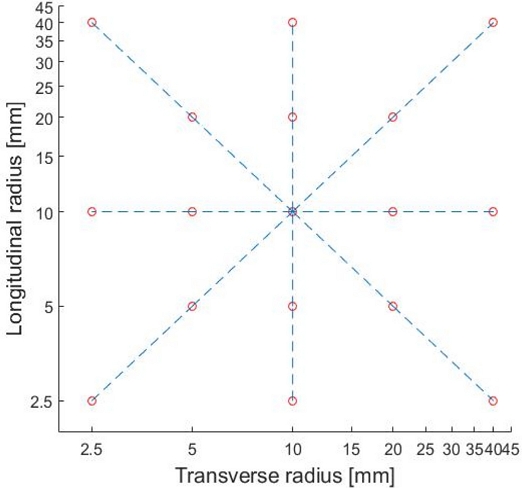
타원형 플렉셔 힌지의 강성값 변화를 예측하기 위한 실험식 구성을 위해서는 2가지 설계 변수의 동시 변화에 따른 결과를 곡면 보간할 필요가 있다. 이를 위해 기존의 해석에 사용된 설계 조건 외에
Fig. 8과 같이 8가지 조건을 추가하여 총 17가지 조건에 대한 이론해석 및 유한요소해석 결과를 활용함으로써 곡면 보간을 수행하였다. 선행 연구
[11]에서 곡선 회귀식이 지수 형태일 때 가장 효과적임을 발견하였으므로, 설계변수가 지수적으로 증감하는 것이 적합하다는 것에 착안하여 10 mm를 중심으로 2배씩 증감하여 5개의 변수를 선택하였다. 효과적인 계산과 시뮬레이션을 위하여 평면도 측정에 많이 활용되는 Union Jack 측정법을 선택하였으며 사용된 설계변수의 조합을
Fig. 8에 도시하였다.
Fig. 8 Analysis conditions for surface fitting
실험실 구성을 위해서는 물리적 의미가 없는 다항식 회귀가 아닌 Paros-Weisbord의 간략식 형태인 지수함수 형태의 식으로 회귀를 수행하였다. 결과적으로 축방향 강성과 굽힘방향 강성 각각에 대해
식(12)와
식(13) 형태로 실험식을 도출하였다. 아래 식에서
a와
b 는 타원형 플렉셔 힌지에서 타원의 횡반경과 종반경을 의미하며, α, β, γ는 계수 및 지수이다.
회귀를 수행하여 얻은 곡면 맞춤의 결과는
Fig. 9와
Table 4에 나타나 있다. 이론식을 활용한 결과와 유한요소해석을 활용한 결과를 모두 제시하였으나 실질적인 힌지의 거동에 가까운 유한요소해석 결과를 통해 얻은 실험식을 활용하는 것을 권장한다. 이러한 실험식은 위치 결정 스테이지 설계 시 간단하게 플렉셔 힌지의 설계 변수를 대입하여 축방향 및 굽힘방향 강성값을 예측함으로써 변화의 경향을 파악하는 데에 유용하게 사용할 수 있다.
Fig. 9 Surface fitting for FEM and theoretical calculation
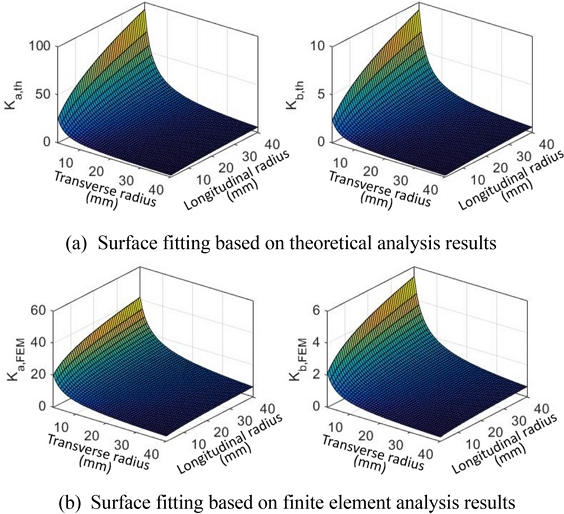
Table 4 Coefficients of the surface-fitted equations
Table 4
|
|
Theoretical |
FEM |
Axial
stiffness |
α
1
|
0.564 |
0.401 |
|
β
1
|
-1.005 |
-0.671 |
|
γ
1
|
0.471 |
0.259 |
Bending
stiffness |
α
2
|
0.0515 |
0.0431 |
|
β
2
|
-1.001 |
-0.766 |
|
γ
2
|
0.493 |
0.337 |
5. 결론
본 연구를 통해 얻은 결론은 아래와 같이 제시될 수 있다.
(1) 반도체 가공 공정의 고도화와 특수 정밀 가공 기술의 발달로 최대의 위치 결정 성능을 내기 위해 원형 플렉셔 힌지뿐 아니라 보다 적합한 강성 특성을 지닌 힌지 형태를 고려하여 선정할 필요가 있다.
(2) 2 자유도 타원형 및 포물선형 플렉셔 힌지는 그동안 연구가 많이 이루어지지 않았으며 본 연구를 통해 타원의 장단반경, 포물선의 2차항 계수를 설계변수로 두고 축방향 및 굽힘방향 강성의 변화를 고찰하였다.
(3) 축방향 및 굽힘방향 강성 Ka와 Kb를 a 또는 b, 그리고 p의 함수로 두고 이론식과 유한요소해석 결과로 제시하여 설계 변수에 따른 변화 경향을 파악하였다.
(4) 지수형태를 지닌 식으로 곡면맞춤을 수행하여 실험식을 유도함으로써, 타원형 플렉셔 힌지를 적용함에 있어서 임의의 설계 변수에 대한 축방향 및 굽힘방향 강성값을 예측할 수 있도록 하여 위치 결정 스테이지 설계에 활용할 수 있도록 하였다.
(5) 타원형 플렉셔 힌지는 원형 플렉셔 힌지와 달리 항상 노치와 자루가 수평하도록 설계가 가능하므로 설계 변수 선정의 제약이 있을 때 원형 플렉셔 힌지를 대신하여 사용 가능함을 제시하였다.
(6) 포물선형 플렉셔 힌지는 축방향 및 굽힘방향 강성에 있어서 원형 플렉셔 힌지에 비해 주목할 만한 장점이 발견되지 않아 활용을 권하지 않는다.
(7) 향후 보다 정교한 제어가 가능한 수학적 표현을 바탕으로 플렉셔 힌지의 형태를 다양한 방향의 강성 특성에 맞게 맞춤형 설계할 수 있도록 연구할 예정이다.
ACKNOWLEDGMENTS
본 논문은 2020년도 동양미래대학교 교내 학술 연구 과제의 연구 지원을 받아 수행된 것임.
REFERENCES
- 1.
Kim, H. S., Cho, Y. M., Moon, J. H., (2010), Active vibration control using a novel three-DOF precision micro-stage, Smart Materials and Structures, 19(5), 055001.
10.1088/0964-1726/19/5/055001
- 2.
Li, C.-X., Gu, G.-Y., Yang, M.-J., Zhu, L.-M., (2013), Design, analysis and testing of a parallel-kinematic high-bandwidth XY nanopositioning stage, Review of Scientific Instruments, 84(12), 125111.
10.1063/1.4848876
- 3.
Moon, J.-H., Park, J.-H., Pahk, H.-J., (2009), Design and modeling of a 6-DOF stage for ultra-precision positioning, Journal of the Korean Society for Precision Engineering, 26(6), 106-113.
- 4.
Shin, H., Moon, J.-H., (2013), Design of a double triangular parallel mechanism for precision positioning and large force generation, IEEE/ASME Transactions on Mechatronics, 19(3), 862-871.
10.1109/TMECH.2013.2261822
- 5.
Roy, N. K., Cullinan, M. A., (2018), Design and characterization of a two-axis, flexure-based nanopositioning stage with 50 mm travel and reduced higher order modes, Precision Engineering, 53, 236-247.
10.1016/j.precisioneng.2018.04.007
- 6.
Cai, K., Tian, Y., Liu, X., Zhang, D., Shang, J., Shirinzadeh, B., (2019), Development and control methodologies for 2-DOF micro/nano positioning stage with high out-of-plane payload capacity, Robotics and Computer-Integrated Manufacturing, 56, 95-105.
10.1016/j.rcim.2018.08.007
- 7.
Lobontiu, N., (2002). Compliant mechanisms: Design of flexure hinges, CRC Press.
10.1201/9781420040272
- 8.
Paros, J., (1965), How to design flexure hinges, Machine Design, 37, 151-156.
- 9.
Lobontiu, N., Paine, J. S., Garcia, E., Goldfarb, M., (2001), Corner-filleted flexure hinges, Journal of Mechanical Design, 123(3), 346-352.
10.1115/1.1372190
- 10.
Smith, S. T., (2000), Flexures: Elements of elastic mechanisms, CRC Press.
10.1201/9781482282962
- 11.
Moon, J.-H., (2022), Analysis of the cylindrical flexure hinges with circular notches, Journal of the Korean Society for Precision Engineering, 39(2), 151-157.
10.7736/JKSPE.021.112
Biography
- Hyun-Pyo Shin
Associate Professor in the School of Robot and Automation Engineering, Dongyang Mirae University. His current research interests include the design of ultra-precision positioning stages based on flexure hinges and redundantly actuated parallel mechanisms.
- Jun-Hee Moon
Associate Professor in the Department of Automation Engineering, Yuhan University. His research interests include the design and control of flexure linkages and micro-positioning stages.
Appendix
- APPENDIX
A1. 축방향 강성
다음 식들에서 a는 z방향 축반경, b는 x 방향 축반경, t는 힌지 목 두께, E는 탄성계수이다.
A1.1 타원형 노치
A1.2 포물선형 노치
A2. 굽힘방향 강성
다음 식들에서 p는 포물선 2차 함수의 계수이고, t는 힌지 목 두께, E는 탄성계수이다.
A2.1 타원형 노치
A2.2 포물선형 노치