Skip to main navigation Skip to main content
  • E-Submission

JKSPE : Journal of the Korean Society for Precision Engineering

OPEN ACCESS
Search
Advanced Search
ABOUT
BROWSE ARTICLES
EDITORIAL POLICIES
FOR CONTRIBUTORS

Articles

Page Path

REGULAR

Design, Fabrication, and Control of a Rotary Manipulator driven by Twisted Shape Memory Alloy (SMA) Wires

Gil-Yong Lee1,2,#orcid, Su-Yeon Lee2
Journal of the Korean Society for Precision Engineering 2023;40(8):665-673.
Published online: August 1, 2023

1 금오공과대학교 기계공학과

2 금오공과대학교 대학원 항공기계전자융합전공

1 Department of Mechanical Engineering, Kumoh National Institute of Technology JFIFddDuckydqhttp://ns.adobe.com/xap/1.0/ Adobed     ! 1AQa"q 2#w8B36v7XRr$9bCt%u&Ws'(xy4T5fH  !1AQaq"2B Rbr#u67Ѳ3sTt5v8Sc$4ĂCÔ%UӅFV ?_Aנj- H>>,m*>fzp"TrKkr^r.|_&]|*vPuܶvoQ1mwVJUhu-I"=LniAƕ8"۲ k*ҿ[yu:.vUQ+)%F DHyVBk>Hy8jݹ q~9D4KRmzQ)^ʔ.J%k_tVi5NTjg!'ky|5asOȻ)R۸ߩFMԿ3L4j6dڜ#NIwUF]JqB/(FafJRzq3\G՛ ?~\ 6)6W4m[O^L0E&rRMض*C .]Unl-1 1r#Rj/&QɈ׉˩s6Rj=5Tg.y.·Pӡ:JJS:C8-2u]d&vUz;7p9 5VnL֢"y)">iי(IDDd| Yj0; LRfS:ktYK%*N2^m|&dğth":ey)uPQZW)gcC3Pv&MMWd&Ŵ۲mvTRoժM03*F3Yd6\8,\hݻ kߔi<k NTwSԪmljj[>->ptU%'LR>&EBH$MQAUx[$Z6vi&_a.KIQ{hyƒ j"JOC9eFҝfj;˚Ω<[3_m% lQ@4g=5$(J]Yc-OMq<Ǎ wSzڗ)k$7VIP붾ͯnV+卵*t]iЎD31~SA1éC2u)ʼnQn-Uoi3:grI8ؓWm*G zܕ)ZקJ}Y YlGeJ6cB2I NS3Q>k=KTBT]W6+SOXQgGR? telˊ%-Re\hѯ2TF"C/OJΩ6r[N.0{SpljjX1“jOsӥ;ҭhe}xu`Ք&.)yO̒ Fߑ.$Qw;9Iw2o+RVJMSOj[SoҌZ%;`d$blQ{Ro{Imڌ>3egf\O֝Uzx"䢸g+mv%Gʆ:|V[N'&ס-ޝ'kfE|K,G&˳98Juin/\\Qݿ̋v~Ǩ!rtWU d|E߫R4d}.qPw*Ӭv5YEcn~f5c%MTMkb-F>5JT,})QHg%{("ӔȸWMsYyWNRrkkJr0XドnͫT}r-jj,Ŕʍ\Q2Ri>v$5!]"JB2WɅ)]VԜUc8i|.jeRO6^V.¸ Q&#|ܶ-*uOG%JAtRZRr]FFG\۩w+?'zչSѧt jz>KW&ot{7P&2D;&\\>Q2JzܗAKSfeNn[jRrԕf6,q,F1tRfԗ>vֶևj-&R'Zi2=xv~Elbsvm8=ӛ"ū񕜈BȩlWau[]ٷBߨF~J!|Ipr3R̴#Yp)={7:G{+:\W}n|Q#%)7^-h"Ƒq:M*%J&$T軨I333׎g_- ucBwwjp[6i25$̏bU’ٱRv?G\~#Iͪb7<<}Ezt" q_Inw,7-d,G÷%T* Wg1"䥱kq/A.,_KhqŒxwvo u2ۥۧ.bQ}XκA$֣ +K״ZUNmڸII{.v{5z5ѮRme[moyƾd~cRݾK'j.\i&/S6f|b=5: p!6i_ 4j6=.si˧eƾtS^c.Y^RJVS-Vi3,esi08?H$GvZgg?gi䤟2adw릿:"۪lkSN>q-4kI܋ێe̊qۅgDoѨ9; #T.Q;7#~_Ufstb_'w~Xw1Xk,vcOt._}v}8"(4Z\ۘgk?J?bm_c!g{HZV]Fkk%~gEt)b秴vΰB|꽸}mp~E6ݹv;7P٤v+ri*3Ԣ|'O14_~7nP{7ZU\Vű[ +7󖱅o#:ǥŬ\|3r%TJX]V7ez¨Y]lc|O3V! R zbJ'PnGqVJ"19WVeOF埜EaEJωqCN5Z g-9[S<$sUK5b|7sn\7x qmv##FF\ w[=-43$^ooVSiXօv7iB۴yg>]Vf"r$J3""32!Zh[K%7GvNLs+4nB/B{vlsobJaҺJR:0g%&zR\ S3T[&ִor*ⷳc3ʊO[iozW٨%$gn:ܶWwFBԹjHP&z u&F2\f;ipW73 [; '_̽b;vib!oec dC-tS__$Xs]l9&z$2/N>%'[}b{h/{`{Ji׉׏ YJB/X%}.|+{(S:qz]4_Kѵo`^tY_4S#* ^zvݾMr+TrkQ g.8Ͽ^i>ӈǙvix>$o( ^qt*&t1oJVu-ql5U6jCЉmĻ*"?JT=K'O/|=Vo}l0b}}f?X[?/\JSBe,kP8ETJ==?.p5ފgbU9}ǶdNKk—_$8̸͓ۍ8Di\BԿ-1v{FF]|.^ۅ{vl12׏z7-R7wE?\nh\jN/Kձr_oBw"N QMBZqe-m:ӨSn6j4%!hQ;sv'm4kcM=!8\m[M4{SMliۇ%eֽR&N:{2A8)THLK3Zj[jPBx#BگMf:G1\`edcʮ?|w(-̮vXt,bW2;.ιNHRR#YwTM"<;mk\.foIDjmlJ;vxy7o7i\,KQŊ9d^Mmgc L*.T6tLeIuOH3SJQ3=F/ʿ<9\JM6mN6=<{xkP!F1QR[I$6ُimXu2An2yԒMU q f[IB-'䤯jYm52&JG\zд\~vdg QtHGXw&1Lw+nDEdC1w|YJmvP)HZ>i0BPβә?R:QO["]I_Jʏۍ>QKyu^bycBq4lXF~l [\*N>-J6,Gq(Zr5h]CwYӤU~ʶߑ u*SIv%ZfJ7)! FS*s_\|IŸZ)J ]ܜi4"z[+Z,MOZ))}|Ʀ(RUNIII.S'ˍO~˨rn}M)xxӕ0 eyҵ7YMAB]ӣU:/ѭ*6bcwP͵ "+qēVjŹO|GtY4V j[mLV M -m>",B$ GD1~j6O4|LxnNmqATNR3ε|DŽa[fmn-ڭ+FiK7Pcm;r5 l8r{#-]'nrFh2ruycb;pW=njRqRJ(d mnpckNnʹ+6]tz~E=ʕ l ZZ5jSi3#47.Lcfe`9؏v囜.F\-UZ:*0_<Νu9Lӵm&)_3\^ҹ3"1n1v_|uRʞͫr'iȧN_kH׺8xXrj=\МH)V\ˬ.Xʸ oVRC}ySU9/OBY먌5 ٿwޞ)rw8Ӫi5*5ZΗcGƱ !ZۄlmpjJ -l <R̵/JAպZuq\IdUS 48wXJJtcg4cI~aqߓwŷrm-v)G7yS^7H^-\mŌAq|"m9IBnF㏉9[N+mmy/!KKۉ%n +BdddfFF6FQRN-U5;Sv'm4kcM=Mn)\qιqUd9F%",6MGdT%-+~ f%+y֛^3SrF>6lc(֪vۊN;g._0Sѧ]ETWرkQKzGe9ʨsKA"yC y2\[5 rԭ7Gk5Mzw_4sM3hxЊ'oÍ5jsub )ͪ~tR2H]R͍>̋m6=%(˿(Wrr-܅y5(ܔJ޺YunW̹븹NsqK ]/QR#"ZMDfD|43Qw|._ԡSqTZBg??O Ϥ)/E_U|i}2 9Z?¹0:x'3,whǣ?C y-A~=daJј&M?D1_PS+Oi&;a @;Dž7[ zZC"bv:jjMQk$M RԸ3uA\=wI.AwC"^.{?-\NSiˏ"b}T/}q/ o.1M}R%:-ZniʒL$SgrBW*,Mw'N\ɇ{s\j]VryG'8f`}'N<*/`U숻z CwHq18J+vԕKss4R53/&XTt1bZƟo\=%nO)h$rBi-nKĪ^ ջڜlwkYm[̑+/QrZo%TQ;TLs($2C:s.%+eoNttq۰kK7O0m_t_pZ1SsSM7"mevFZ[w -FJ*T*jФQRg BSu|]g:ɵzjqwmltL.e3sRMچkSmjkmWœިm++¦'tILk*բQ D,PB\lI[9{%Gb R6öۍmX-MaʉA931cs..G4CujQտ[9 }G-xwl)IQz j Ó"rqe&=]꾧֎c)<kӳ+0JrRR3'TnXi^xMF Bު*tIL.[h"2"nKzZe'ZV/RrNYz]8죝n]Ķܩ>^Ժ]u-7^\mZjܣ9+Rmn ߑv?oꋘ?&ƪy^N4o=3-ؔ̿*`}V݁ ƒPu8%$ ݗ]wt;\y\>='OjPIp/nJU8{϶FNMsf"ίNqƹ(+ ݮF2Km |jܴZs%zf*eȫ?]4)I۵nR&FX + [jDh(#哑9q9Eծj8noǕZf\J-l&Z˫}`ӎhyrΉn\űn]9pʌӣ"׮Wt?N4_I_~54#/my1Xr*척aS#DT >q ssΛW;3oUaJSRMDgQnt:Ql,/ ܷfRqiM Ȼ>Cob;A>ڦWقM9X~/!'MW.}Vrߔꔵ!5|iB(0-zF=}okڢE$^wW~nokY߮\6՜̌{i-AF*9)\t9IV6۸5ZUF6R$ŨQIq砳YUZ]eyv >hI櫥N )&l JulwE1GDOuFN2| }馥uC1rޫV+^gdb&W[4<^e4YW,d|htͮsUM)۸8:{3d{AѢ)~ \#J=NdƮꮓ90 |1K$v*?мS ]i$J,C,SG?/_՜pMSƯM|mG1V1$~K>CSvkuj=&) -,yLjuFHK{c駗.SOua;BrSqj-ۍZ#'Jys7[g2z/.u4+XV2VQ.ޕ)$"(%)#Z7suZ%j }BǬݕe)Jvz8zJf:hIN|svO1O#IEcۍjݽ:SdὮvu^@:o^5cs>i/VqmVm]ؔܢn6'vޑ̗J4Wn@OlKbX ;n:hgJ9ŻyǑz8f܌q&Y fN0N;[69 rbׅC2/#kE l&2~èMR.*%g=Ft.%؝e8<.e=Uv{~㻏"EˑnvDѭ͜Lu3u0:U֝$[M5<:oi+V4V9 6nXvx&_ q Qqw3W:uϔ2yb/(ɳ|5zQiJ#r|Hw#.W?4aDŲ\ugWG;Cw鐢K|xg)##=O.dF˟jMUvWĻsr.z]kPc9"]R)mkfOd*uYf١RsB Aîh=k]ʳUrrZsq`d#r$/Ը3o^&lRWȍyuW̦Y4QDUMJ65ƒ[+ygk XK_±k#y:8(TJOSQhJt2.DR}"5[) r)6V6u5k:eXZmv𭤔!푊Q[qQ}ҹLE- 8qIZG|UM4j}Mܕ[Vwm{} Naqµ"ԈM zOpKѰ?IAD3Ir0'/q1itoB5{%wkOBn-ۜduqIzYK60{+DʕܞqIt";r1mG/\/ym[6JƫR \L=S=OT@Ix[TMm{>ݾտ֒ݸӉLYIx>+"JVNzx||5rI?C{oz8۹e\R-^\A2F R+N9 vlT]"ۭ d)t֞i #E2jB@׵=#/N+!ĕhx}I!cM`ąZ*ŻɄҒ߮Y.Z}='/oۙ3IpW̮hT7cTSuz9>B}΄&h!>lӵn~j˅IvU.'v'CSZw8QK3G> ,J59ٷ+HSg䧎hJdzvwv-cvxS5[̊n~ؿ%ַX?O0\6ne 6kn9.ϯ} *h 8_QhLݣ7q +=XBҲ5?[[)+F`=4 }B,sNg==u*Nj9k_GJ)+R~GSPBȒZ:(K]heL=vKPӢwq(NrG^ثϣ?#tC?.ͼ[ۅo؞y#%ǛjVyLSw%T*s92JTM%"YkQО.q)gCͲn8cgi6j1MѾ[{9h^vƘǚםidfi.^RHmg&rׇz:}݃}xT$ضk'5s-狶,\vpbPD،=Okf.c#cdz2FK5T!&)|ntD<+OŹU i-G[EE*FDfeaf2QƤM\UG_{ǹm%\yrGy:.\4wjPGUJޕUV7Do\7Vy_13w;[?c]H\$IJ,*L]3b%L{y.JRKG2sq,B6T}(#nW|km+q5] r㪍bJ@y{byz,b踊3ϻJ,'^xd،)JVw#.Vټc''ÝպWtbRؒJz۠8!o9IۄS95E9ؔ-e9JR{dmnｯ<[~n${~Њ$W?&ՐY_? #a.ߑv?oꋘ?&ơ|y^N4o=3t=~7!/M3>n8W홎2M`Qx+ z qy8%]7_~540ۦ彷]Wq CѡwkďyF5Dum_}~P(5.(X,K9vᯐ?leB9;Jhm#3{CxGE-S{;@Fz˙]=O'!ɿ]' r`:7'2bЖ>Iy,/eTy/V<.H?UYY{\^#ѣr9^7?xoRȆ7EoS_&??zϾM?(~Q-K&>"~aߨ t7Emsϛ+?;fCr)fY+>z$tIkjn_>vnrֳki-˹l= t;'EyC¥|/BLwBJdgjۛ$s S1|ɍV%JI6KvəhzIlBYɒ|0"Sy0F>eo5W)O+X˻u';v)2vVq۳kۮws?UʑBǴYO漪e2MIjPAک\b1)DDؚKm6ZWΨgȕ۶yjڳ 2ضN[C[|r@9Jfo<_eI7q.|cÊV߷:i.:$ȋ)1%%)ADZCEBxJ0MJۥy(bNsKM9k43IwNt.\%N簤I'.j|ƃ2$grBEٌ\}9:v*!n7M(ɽ]7c@XxƱԨ37īf62cTTfFK]9wntQHͮvٱI/f|j=7}\_V5U^+:uljSȃY(XI.ȱmo1甅jڎIZ2>#\*:gY|4k\8ZwSqtyA!+];бޞKծË¥e)#5ap.QK^8VdU{*ѽL\=qmjnB5>{ Ӟ`v±5 ^k&O~Oshɷ,;6nOW>u6{RqS`)S%jp\ipdEBLfTWy$GIYw~䲭J.1vSY5z.V>^+Ǎvc.I[R{QsNR3ӎfhd>y?UJ*}~[e\i5U^͛E]G_FS(Iɿ]i8:4zj~շsW,ˆsy:%O}iur]iF5~3M:Ӟ#N06)4ߧgdawIotiz:1r5YDZLHBSi;NQc44la=Y kQIT*ըl:tq2(է9VO4뒳܂~2rq'nrVZŦ[t7\oլfb/mlpc.I8콚q^1iE~䰳mi[dۧw֤ICfdFeCsg:i| 6擣׋* 96lust^{%99UNRvaMܽo ammi$em4D6DD\nA%$$#}۷/ݕr99JMն[oT޲E"KTaP+HGkŴj5TM5xƱOS-k`ۛkٝWz;{kS}F;~q|~^_|euwnE'pSupUP)V]vE+t =ZRaVdG6= *.ϼnj9:UɷbېmF_tޫgHjVS'śǕًdkkѻ_]Kv?nT>)^e=Ar1'3ԔILyD?:-^in):{7.؂\.:V }#뺾.3r̸*xbFM aȵz 6SQ:ײj[ 8nn iFMw rR"5M5I旘35f^j='j:nNW.ʭocZvZKV^ɚJ.cM1ZI7E'6rg탸5oZ=[m Z`\hbMUR١Ȗĉ):Jin!_7Dй+f̷eKҷvͨBPR(V`y6tw*MRΝcB.ڭTnc;P$8nFvm4(D(R#R-L -2:FP lxZKQc6I("Km%$E, 78uXIFA$RQI$JbInG]c[ֹ:ZM+n^')JmJMJRu{e)7jQDw~%yQl}BZujSSf۩QZ+Dzhd5o%BIc'GZ?}΍:>Ɵivז-%݌J5MqGWTVʦh݇ܟ~Օ_6 n'{3~mϬj'J11OȻn߃r Qr\3y٘+WӍ'WxEs^O3 o~[|7>]]H9݇ZomT@]?5B:Z߂'`V_+/MSKX߆ޠk3?o7y:4R/7þ] iG߬aBRU&?r&/} cQߥGj2?C5Yśe7hU=?+ x龳f-܈czW^7p%-(\D4h{UK&ӡn^m]Fݢ:`δvj俜F+) y[{{ 7 tu>gvrěOj'5 iRg[ͶFjGe n~qT$ci ۚ0oԹc*jL[sVWqj\ݻ&6"WoK:cnWmrv)o>66(F>=W^bf#c zzʞtپy%mՉPël e}J.\Zk4ttt>oEM=q)hJjI=ͥ(%]脼_88ф;͛gWG;Cw~˘$4=uWdĜTثNDkiQL9U*O"4XP`02,Ge-k5$h>ܼ]3vr6!9RQPIVSnM(ۓ{>;/Qͱv{3&-[rc)ܚI$n{Sv3[j00)-D3z}MRzVQпj,T[uVs0\}Sid;r(ݝJ>æʺL&c[jPK0~d(FKÝW\m]GTcF|Iׁ)I3~#oX%vҦEݑؼ5Żv2qAZTE^..M{ʐfȏ2##.R}*KʛZz^ӞN*lPťLf\G6[WVQquV]XAi)5J!,$iJ6o$tPZc;Kjx_n3`qIelV~vLy{fn匋Ѿn%;zV.n'-ұdd2߽1bZksPe3TI9)$ԩIN9Vơ\=2885N\ p)/a柛w9g_lױo8ݷ iixJV& ғRi{N^_oAŮE6Y7I$Nk$|Q)-*4Z)^¸%4Qm [I%.c-OV+C֧R#%ѨCe3i;w$G+_dy| Fzj$DI(=OA gj%v/]8qԯNIS*֩',Q%\44ZZ%D|Ǧʴ6&vֵI$%8(ԬƾS&#Z. }6z?b/|Jl{ץv&mpx4Z$”ڝ4-H%dGKfM:sKSRWeJAn]>s6应-W9'H]'uȫYvgK^\czp|My\鏩w/ËQ.)]\QiS`8uL뚛̸=J"ܻi\å'-)54Ue]:K\퓡vK xwBqrH\*֕TnzC.mT=t-H]SČ~Nu╏NÅ3f|͡G~B+Xm[Q7U{9"~jgK Zoʰ7"qJ,ekSeNGgϳ] ^.6:s}_,%eRg<5⿨z{ZPun#jRІ.6g T.!]xa c#jN$Zpl̋H WZu8WmMRýsĮ?Mco~sx TU҆Q :KDG4n42.<3/'^?6/ܠڒ^yrrÿr2\D}}B]^E~^T cɛ7϶Y[<֞[7d}2%QPqOLEQR\CIsj1?\}%tJ0e~ *sk"*)&ۓEi#{1J8Hrt|'ܝRr8)=ƔN'RVz:cf]F7bZyZUȘ4x8,#JG̒?.W9XnO]KO]%]ƻ O5Γ/3qÓj؍/r̺rƵ 5\&m6h.xoeX[=<3%< lZ"2h\Z[&jW3ejm?k&[]ųj+{N{66leu_+lj]q* 7g*knأYv= q ەdxЬZ|%GUrQ3jLŒqET]1% qkXYūYc[7Ś]QY\jko\</Lc7+'hMSUc6qXyؙ~6#ѯv.0$BQi5YyIhɍiy=KD!n3Vm[V%W-B%swa97ajۗ m+9~]fKq|Ddaˑ0A]_v޺mM5* F-BYHJ5}q>ʉ.6hyDmpD׬'-_v5;5[8K[viJ.3dR:oYHHh9I7:۽fi+wm^ [)odPѱ52CZUJicSw\&_s0uBȍh32džzQflcd^m|7GѹE!fO5]]H9݇ZomT@]?5B:Z߂'`V_+/MSKX߆ޠk3?o7y:4R/7þ] iG߬aBRU&?r&/} cQߥGj2?C5Yśe7hU=?+ x龳f-܈czW^7p%5|Y:SJE\U-(a_cƣUǽXXKiȞNlmۊڭڄR!**ܤMeȽ$|X5(Ź\rJ~ܮ]>'HB0cp XFr_c?f?7<ukSgov¥iG>>䙗i.+t+bOjIܶ . i^:nm}s}(3>NZ$2Qg([".>i.ƾ)B̋M8+"- >eE6DݥJnJˣt׻ 5.˅nJGwZD~!i۶a,Db3ZQ3O#KO5/֍ozuK'GbRi᝘NV_ҝcvם ZoX}F6z 7e5_e:ۓj=AB+iܔERadMBq*ԯ DwI/Gy*mĥiRKg6skY/#SN4e$-yXM YL?^ĸNNӪ{$r1JJRSLO]Aqm>V/s[~i/j+m>z}eI"Qvp]{ZԼ:{vPAG2=T͡@ڐ#u"E*>C;o$~C#_d/HBq^YRٽzIKbOm\~żjFFGdiQ(*/i*#.FF]©m=BmpQQQSP&Ҫ!T&^>:y)$ˑÐFčI Bӡ-t!bM WҦŶ'UZ=}zvn~oT/\ǒ'nr8 AJIӆz<^uߖ4eFC1i+v!3qNyߕni?4JZlmYFXFۼO0B\m[ tʄU3s"Sr(NJ;SKW72L4̏BVdf^Ҹj\]ȱ۪(ӷm?J-KEmWڽ^4<8qu%9pŹW~877ܾeVгS(յe^C]yX͹! םm4FGȋ\y'Z FX7e)|Gjt߹#gb\ŧq_([R8[qU$Z (ʻezV2V!iQ,i$JE˂٩ a(GK'O{vnBvryRd-RK4=qxZJMl_CuuIz @Rt㮽޳!|68\-l[џ84-2Pu" RJ_^OL>G1~XnBŬw6J0*Uvlږ1N G1q9IUm*'oWu][&UyYZbBZRZNfEJf"+2nF~Eû7n1xv.RUM$6 lAxSQJ&n5ܞwlEói"#>4׿Q.nEq7Oko[1wg8ZQwZYiqtm&~">Bo?w͡ni2峋NCEy Ҕ+%ZJ ʩq*fpˤl,~^Mχk1+:ݕ z&Y`KLӪУDr3[*Z :(SL&ݻ۬Vqsyԭs x|iI߽zZrg.:mp%6ԜvgmpIUt;QbS.Է) ǨKSV,*lڌ|5Jt3#NP.=+OZ~/G سIgbꥹJnl_DUM\iM!֔wVZuԺ,yV.Q>f v:݇WiaŸN5Ҕ[M7SsrvǣrMW= \8ZW-jsnڕ.ZnF2qt ً[ٻޘY۷Zm"Jxr&NAfA-݌to9s359݆mZ+N1-qS$D=17 x׵+%_ ve4ir6Z$FDڗnFtOr'7'{9C˨ꤡaYoace{Refnft RR"4%ʌm:Sj3)OdInTO>X'vxV#jܮw9Fog;5.~Y5\~18YQܹvj4+~t7S ﬕs %^۵ڴDZV69R^Y+rj$ԇoJKR5wB9C>Y:l+EǎS{ʲ{T6Wi* ^^9k/y/Cs\g*qڵgn4T8mERr|Ti+iPe;;.i\EBEJ 丬i9ɧM-ԼsGDrZ>r#R>~X9y4b棇9JwV۔%m(b[Tjvl}۩~nDԺ{Zo-YuK1vx.nWuO+jN [ٮ0%"΢CdTJK-RަH"$I(*ve &҉FzB,_Vpqp9m8werv')E;o&QE׵^d9˦j\_,ڵugZȻ̧8k+jK{wmr@3ӭ2 wFkzFVqs1؛.v'I%$[iT]D5Dl2 nk7qUxԫLS+sا3/ΖeZYK<["%-g/kRs:f3;*E ت wJ%)5&+&rw*霣i|sMҴ|;R+fm䡩.!**dӶ-6s6,]zAXMWjmnz%SJߴm2UXw7MQ%<!tKys#P,W>s;3IYwx<+i_\\\U6 u7P|xbn_k&ӓVOe䦒 VUr,-㘘"-LZeOSҠթrEvq8Kf%5%&K"#%vD/.ZYYŏ+p$nZkvއuW9㓱Z G wYIFyf)?ƎUm5ԉ/'k84{KO:rQI}XRuԪ|*lu)3qZ[mSm5R3".Xcَ5c®ࢫI*۳~wRϿQWޝ(EJrri&ۥ^ʶ齲Im|[yb;mnm֩uiܘq>E+Ikx߄3r33-5𹻖09ϖ9[Tz~mr5NsWl$oPusޛ^{Z;);sڹf\3oٹZmԉ/'k84{NO:rQIBø8Bݱ3n֤DiK4u& ofSȒܩx<˘|N0Fչ]qsp"}! QWw@t4ӭ+cO5%]'*{eM߲DRO1y*q8w++e!c߶ܪlZWّM欼 CQ̼빶lX{vib/V/ ai;x6~]+z]MWB>re-:lgk}պ!#9?%܋V-c[z!W?c7YNm/jRr[HOzԻefճ0q15Zp#rkQQ0tU-AmڵP/cȕ?0cZYj;:0ZM=D6g ?'UN+ձ[K ܖB2'xq9{|۫N0ku 7xaj;n\ 2[VznMlWiKbSk))f..)Km)&bGZ=>OR܍W:j'rM'wYz&/鶧{Sʵb"vջq[I-ՌZH._x*BagC'T(Q:$ͳQcMCKy?3g'ߝqnT);qs #ؤZ}OOI:cfnc8W~qy.;^pVl]Hԓ>^H^@7-AA܃nmL(uWܻS߿ Td95Bdh4t6*dDh!EhI[iŨ\L.&Nc ܮf^;$R)\rip9I|ٺ?#R.ZDZ;/]nݻqs\QE9M&Bd ]N mN*D>tgbK>+ˏ.!23]BȔR1ɝ^j'k2ƮqBQq[$di]icV/e`޵B.FIIJqbi>Ӥ|p; 6${)RU>_e}^dzdfzi %ekRVUS?6'hׂ)5.\+qUgzE2C˷ecŏ^֔ibk shesFWJ#~> Wk~ݨ}ڶ>ơǚ)׽ZƉo~B-ڼrvoE:Ʃ3ۣK7+Y`WirS):{>ڛ}:wԨ(J_";6R%[u&ƫdZ_\'np| RJwNeTW,=rrbnkڄ[M3ܴz)3- R.?:okۼ0TU'w{6&w7j1z3ON'fGoO?)S_bQ_¿R(^ԴԴG.EtMڇ&RUiW uQjU> Kiu1d<ѥIQ'RQ1:O/lŗᏩiʂv&Jc{D5 Tt)1.n[n۶X}RjqnOʽ(~[Ns{ސ⛌uO,kgo֢dRNQȄ .'6W!׌P朼tdZjFGE"]K@'i۪N;sI[{SOzk>`rRR+!σj8&TjlvA̷Q?HyjyLHNտJMjܶT۽lG?SnKN%<‘ nq[N0Sq[Ta(&t(|HGO~gvkݻTR4&Z$#ViOY1r$6YF?e4U/Mvxų:zbU^gQQ+NW_'4jfz^c'#`rvrڡ(IJ/J ݦ6 ]-CW |_{v*_q3^DZ}Ic6Uڌ8p7{crZq5ki`)mU6|-Z5^iEz3P=:Cu7DF'k%}<C-޹ֲ̱#\,(f88%X-N(ck0VLR~} G"-8ӏ/ϰKq?(#nrVTmZ;zióM4 m |UT'C^_1X.gXM{%ʤd 4\ovN":"y-,T)fLQgۢr=/CƹǨJVr[a+!rT|%Y\ٱzsS>jͱ.oOc6f$q% ǒGo;n[];ߎjrk{~\VۓNIGn:iqxo |~t5)Rxעri{Vi&NUOl_ѮMfsޕkЄay.0P{7N((BaIP$ K"U6Gl ݙqJRu+qN$ m#*p<|{:>-Ev=86N*MM긭U*uѾ?/^o7;'u,h4݌xښRM:5.(/ \իU.{F^rmF-Jɷ.>Q"[4xT^OZ~mK}T0ݛ^SAo9u?lX(' qj%=X}"^e4wˠ|rܫ 6I\Ķ;Ӻw!'ڍWg{ i U_9Avhۣƾ+:vs/MK[ɭīe{`Zgb}r[i'GE2J7Nez579wRq+Un ]J.cJ4M:h箽Wxxm^ pc\wcN%'My $$| :$Fqɏ¾^қP9J6Wxvu}ݵP>Z'FFdg"-; [¢cmWkÎT8nG%ݣ7*\խCLRYZͤiD&J#'ehbSyXK|y*ӞpS̍R`[pTr/Eg)K+92{_ n3zwz'oŸۤ+sOj J:`T>Cf*lwd\fYOP"R E֢̔L4ɥ :;.b(B02rJ蠟9>V'9M%)IqnhP<%,r'P/vNSwr#w"ݨaqc(|{kd=^0jTMR2ULNz|.<|^PfY22##!,K~E BEJۜ&jRNsHަޛg\r,v؜.jK3)[EJ2ii{KEiHP^&]Gn8x=K}Wx/KI9-ϵwQ%spܾ[^R}S3$qvq8M[ ozKxcqmJ/ӿ{_}7&ݨ\f6ZSyQz& 7ۉ[8~UNn|nkiTB+4RI8'Nc%tn{!]Ȋo.nEmʱn𵵥J A+wy#+ikǒڂ;՛s85'KmE:Ђu""Iģ5p=БbTY-ͽڔ詻ngL2Q}$de# fs^o{DUUsfwӶ;s1T,ǤtޒQ\෼J=.tKU,7čJ5 N$y3kdSMQU~mO[03 $zAڟsF5^뜞"Կ QHmrR"ӳηer+ҔZ]hE-6Jmt'ޒ=O[sQj)6K}?e4v_KfZheޓ=BV[bY}lݒTTЬ{ȫvO_qpRApVŗ 6ju=*BR)g "O1yhb=tqJ gtm\b3RY+JQ^Ō֍\յ\>+uSi{=x ^w;uӘ#ĸzLn*$anok߷CBӷ}5Yqvdž<( "_OWit5:EZj2 B ρ1̊fi[n!HQF82q1牙nqnEpT(2RMoM4ϳOu ':֧_Xjsg jP^(ڙ{2%E͖j^}ZU[Q$'U) <܂%!s"m R'G5M0<+zM6qYm$ڕ$3ǧH]?o2N<8F1̻r_my[Rf59NjpzBnl7*{.QP 3N&^BLJPjAHCK2Q}$#~YMq8 k(MFMU)8MEqTy+Tʞ-ar5yܕOXw!e;q-Jqܶ䓊Y:LC UE{/t>r"lI9)3KJjϤA 6SEE$d߇3KG*En|P\ԭTn6I-ƍKTj<1H_zwGr19wF N8ݝ+a9ɫM6mhePi%mmD! """"""*1bRKrD"vnrM۫mmĽm]ӡiG~e"˩ lhRTMk^MX["Jݱk7_ޕ*DqĒ&flՒ}`W}~SմZ{ĕ~wm*/{{ѹ_-0ط#P]xlڱ~Tn5wi*lڪ (JxioϏbqKYR|!|KN53 OS222$jzww%i}>N)E+rۥ7c$Ofl/LNث\6H9: FY󡈾I)fB֔JI_ ֣^: 9mY{66㒢7Uj]:.-os[R&gMF3˸#໹kmjq^8W"PΦURjʄWa˧T!͋ lW48JB2ko+ /Nw QwQzQ ے%$ޓ7^YL|r7!v%Trܥ &|M8~ybrn[RV gSn{{*#2#ԽᢏӴHak" ӌcwҜw&RJ07ױ>Ļ =^ BɆ)v32.M1=#6%̠tҤnzqMwԣ~s*%-j|_m*.Yx9Sz=)qE4 3pk+,`=kNRڥ=B=nŔNAx)Q$ԩȧ4z3t#Z2lҮYn$S%y- JzGpu|LBV7ZW#;Wwipܷ%(6jFG5#{$D"uۭ~]֫SrD܃fҎӾ+Tu>-ZTQ& N|$沸ii>eRWݳu'[O̻j8JۻEѩ[]vni= ڒ,[_%kC7I3Nv$4ɎЈeٸoUu:[}Do5|zNq=Tre%ɧ6&~DȍF]ƞG5q m]/w/ \ʲr8=oʔe9U(W"|S]uZd#?Se[W"ֿh][-7Nu:T=)R}.;ml*5Dlf $fF(̏T hiIUU4Szɕ t(%_|2 ~6eM;TƗK[f&]LK^CE2[ȏBOd;Mi|cx,^6;sیGpQ\NuJIFTJ~đArh* B"$H쉩eXPRj?sl"ԥ)su]xpԴY%VESH"ЋJǰ K&5^Ukzׄ8kEgS2h&Se\ Yl]WҶp-ZUvi7QS:4byqOo+[̺腋[6-_Fo.6[7$p&^ _GZԸߍkc.qqoI[9m߸YxOZЦ1uoiSH)P9Uʄjcq= S>֙NeR><;+ڌk%_qT].srNO?s[=vH[]RZHRMtᩗVؾ:/~u)ԍdg%=edVrISb{6vSu=(ܥ)mTv/J}̇8 S3ad:^hBSf؉OɔLhI_1d8,L><_A0y3rXq"'(۱;mFNII.v5_(^q~X>y{3צ I*Vܛv/jW' T'NR'j%ꔩ:mJ3SB}΋!-H-RJBТQoedi9tjENenPpke.%4]#{:>mkEɱdYWl\\\'nRM4&U>?Ќˉk÷!𴪛]]5}UqG~ݏI"O~s6(Ļ)qO~h}uԕd}Q~G,oE!&G&/]_H-O=o{k\̭bkv.Ô܈+;arZx)m?M\3lU$mk-CFXjTv6u' g:Vn_*qk:VC A%'4JV%EY)#BғO4<e׿jQQ]yUr4=wm[K1r׵%Iũ-O}|kC;/VcݩWZ)EHdžTru]8hgĵ-;=>U_ InvTm_jBM+QiF"9*{DI/iuo(=TzϖmPQl_v4z>T*ȴ>YF;ε\t]EH4ꌇ[VrLzef 2T^V>g2~kg5~Nק;{~Z~W}&ŒBӿS2$J?~(Yœ"˲ߩ\O]: J׉ښT{mmIѩn3˧)4LdFZ/zUG>U> n 5& ϴ-KJi2o]uKljvK3$bԔҚV旧iY5.ίfi96v7!v))FJM4{jG~Jt/lUE%pTAFe4qQk\ve۽/u/Im+W')v{\-E|Pms7߮DZRr۞/mu*1ՙaB܆ -xg3#6ۥtRogʌU)׎]ZҞNnŞr}F1Nnޞ;cZ{N}ۿMiuxʉ*3qi'9KHQ$WJxXyرŔe~[v5~/jN9Q4o6rJv FrdxM*iRjMzUinHdн7ᾞS=S'7 } ̽zt7K|_g J=Lq+/Bw_\ۧx\HJUPzQ<hqF[V0x==CsU7q|^ {)Iq38$_A(VgcKu06Ƅ"%i~_ˉk QCܣB8Ku/񋇵u([w}$F|8TՠI.E !;RJ^}MɒD_q2];Ɖ{5}*n7nEInO{Mwv}&q+v [V}Ĝ@%>#dXQ$f;iep.GquixVt x6bj͵mlKقQ[T]zs/&yەnM'W}!Fp_d^Tu N{ɻ'l{խ2.sTu{W^H&;1s)Pӛ6>$mě;Łnj= fLT)>׸+qReɴ[UR\L*P/!$Ӊ3Q 'K=m~6XqW3^W+ųO_[F$rR*u"T%@O +%# ]˽!aܽz{ͷvQh쩎]hGތ5ɇ*DzJDRNLi 4:{~2FmXY-zzĽ^f=]uū{/+&c:Ma{ĝDp2m܍kHș/(--m_vݮK(V{R}.k&yƴ7i^4@3f sK3^Ř˸B=]?gt5KbZB<e;kQLpxuWC}n 5ҴepB##~q= `x]KWF {GfŲ}?G.I9pjWkU]>={7q{kO/^I3==f1ɏ%nnʫ/Zu_yXN<57ۍ'vy/"8넭M2eԷ&Y,в33%IkjMr7xf nmQkX4踼>a-GcIeތw&U=-:qnW)z¥j :WqSZvԒ#j"KrIU)%qrmRoDGQ~SYRsu*V)  ,/x)MFD6O#]z 96[Ui(JRfw'y$GeUީkdMF-ݻ98F2d[o{Rn0n-xsV6Dh|Eb2E:KCOӪv4SJCr"J!!m,hRLD| ZYFm/X~ΧfrN&4Ƒ=Z9Mh.Mܵw/BdrܥniŪ8ɧ|y%œ[M=_tj?F!z5\evM:\ ~F-sg钬OWq“iiȍ<Gi%%n2rqͻllƑ)okw7}\Uk-:&fj솘XerV9yZuʼşdFC=rmo%~ZN78X(N)_7.Εn1MpJ}62jjJdI";R5&iLԸc:jmqiQj$ujp\{;v5B񥍪Xn Ą4qOERjzN(Ga٠䌡)p*v(J7#ZۻZ8O W uONb+^Qipv9GvֽƼϯrYƖKGJQDNPhRJjᡧC"21"9ѓS1;R_O7/WGz)8fE%F2ukmvSov/iZ&/]~KmI[:^~ͤ\kMi稜\ywJt3W7 8Ʒ~ݥeFgѼw"8VVSج\뻆}ݭ/J6Q)d|)zU3>k\L=;ow֯gN3pKѫ|wmkZ$z^2R:E)f>ς нd|#׆?\ǔpV{;\$ƵE%-ͪm0S6[n< kE[}mvE4DDZ^$OZ0*$~XUv҅B@^?]so#%ojw;Y#SxxueBگy v^i-)s)zV jC{7Gt.w3v,ygg8s]aE_,*E tY5k٨h=o"m泏:\6w噓aiL׎n^c\75AGkЯ0Lf46َ`egZ˓p/k;̛]kq!ݸzpԭG"}R9Ve>ˏHUjJ-&7nrnwG*Xv\˱/vN}O)ʼn&CV͍f̵]r\PMB-6Du-#RͰtRN^)mT _}nSȕC*_xBuTkJW[`ɩ`ejvsngP ڻ.-WUtܑqԹQj)t;vN&RNũT+8%IXӃ5fK՛-d9 ]CƑm|nZ-6=Hz,*aEm W3VzRšdY~Xf׀Xx"]s;)5u*ُHB BRGS6bݶؿ 9j[1*jױga7oX CUI%0v#~\-O-Ꙛuɷ쏪&5mY٦M`LJ2qK~HZbr =N'YobI. (^ ׾{_ ?OJ`S`3BN[}5w6:ǵ/iSlt=4F*d&T4y/#. ɵim5Uֲf 眕6Y7 fơ=3dϕq뚩$qTM-%r!$@A? ޾V0c~{[{;򥧅a~ڵ»&ڄv1ek=wb MLkNAԬw-x>~/r=e73VeVN)K%Sښe"+3uXuچrn ֺVzscJ峻m}vb㶓n\YbIUBT%*,0nov=;z꣓S/nSXSpl##k9mXGrZv^Gde!ŷRԠzQyjC]`gToPov{j~KRBMY}i[߶9KL2ԉO0K#m>wB[ٍ+n[[b٦DX ݲpo] [\m5qdT()mo4Oy9Ie b][wղmM~vmi۱~t \}$яimRk(L c Cvk7r9_r1 ;zv|F@KyZ[&jEji/"6$69ml#e]9s\{ScL}Ȣؿ0q/nZ*t,CLoD߉Njǚy=Pgmu6^]l-["çUʖMlʍp-"qmU>۷uFOJ%Ǔkx 'g=睋k[3u,{³WɘݪF]ՍeFX"Oy\,cچ=w/gn Ļ]#2? vqy-gXnR.^}ݺFs{ŝG]}e|#0mjx"ƬWكm?rgU^xVB":Dt>@LRbun~ݭ,w+v⪕;\U(RYa61>#Jm˞Μ9g9XKaG='u8gf}'qy#ɉw J]We.ʲ-<+&q%s?2dњztҼn`cΤmmqMdz O[-ߩӲ&;[tmܝVnr">{x<8U+p:Ig]zjGkt,uzf}dؠoJaکqEq -(:d<պ=eKy[˗^%ZXkX[C2߱\ITTLGzANM￵i]K>UsOGDDD.ZF6* ҃V Zhz{'xp^`wo8r0h ZmJ5"jb[l=yUu7-;7IT%:jFjߖm0tzU'K)څNۧYJ)4IQ}^KWm7kSP>q;ނ#)'n7&׊r?óM{IwR\j2Qn[v pe#/tAF\ϵ225q֒om6z})6҅*oqDsMf CNIN=T S2t,_ѧ}kveMF0J\Rnnݙܹy[rUc-j{yGtkQ%s]5qB.Nw.JN1LvR Ui5J ZESQԙr):MJ+g}χ!2;q([jAud][ljVK3$ײSJI=/|&tl'*n۽f.frܥ jQO8>&Z];.|7T/C}$ڋUmP2Reҭ8hFF\L 3~e v\۫]ݝNmrnB%*]Z«hKc=BTLG :V74$=Ǘy+EX'4tn(I:Ѝ;Df8c,k1%dJ6.j6ź{N~l6&*fœI7 WAlGOu-ҢH,,(ǔe뿋쩨kM܍ZſgRvQ' 9)?n|er˭|I|-fGK.rΛp8XV1%K6mvG+tc+qE&ǸC_Nm:l=_/m5^[dߌڇ.c<%:)tQ$Ow~-aY;UJ>=F)2[nk؆?훐M=l6[4(O.]2#-H^n#->&mp5~Fӛ+|| S,xag%qkEUzUgæBhߕP(7]kFnq?֖CpruZ6*rEڊtS|*tI*E}7R<,nUU֫^I7Q*mSly%rdȓd8hE<9oHhMfNSRj[i7D[Rj݊+kდq{"$$H?p\̅S?㭻;t~R߁)^/>Qj`yt[w ԛ;²~+ߔ_ YW~|o]?x^ᯛ `ʼn;g)T@vWn]>&4lp+$D̢1l|ȨF%-}.9[}w~ ԠLM9hСablfe&QoW!s?wjLK?s7yO>(=C~_nyǜu?v3vyo oI@qV-jeES^[9WoSܝh"l2C1a͔CiJ@3:Pճw=/7ovuk+\V;lDgն<[A+rX~d;m!_s8ݖ׷;;.0llUC+?i#_crʙ1~C.\–q ul8Hܶ2m`ܻM3Tov|Bs rɵ"oLS- DКw=Tv@f'6|YlD͓Y%׵-#Ѯo%:&!3o%\J<02;K87>^vgƓ# ;ݝmz^Y6=PS39U%~ &f# }o!muH;ʲŇ˷yvP+&.7e[3'vR4Yj̗IZ`e˽3o[WU{ m[sUbۋZǾۆl6~9'V*.\S2<Sd*zY[aŶ`]C$n.v^Ʌ dng>ەZ,Mmϑ :n6nϦezWqUJ4! ۇ4R! =>>Fn|Q[{pRO17ƕ~._I''00k=b՛o}Osðc2'o\3}ݭQ^2 . R1yKȣtAݿ-uܾw!`?1Whn|gzUo[ECWwjUIן)^h#1ɭ!/Z np;o;ΗŻkXs."6E`Z1 עӐ9Kl8qd q} 2Stt;#j>;խabONŗ=fwP1j)l6J̶|gV2`y/0E˛6+ԫ1? 6}KW c\KoKͨ2ۅFw–s*TԞLיuDx .kCzWXhy۶gLu|%TnupǺl-S* PRaLnT+c+*xl.v!.U=|; !_L̎뱚U=4hm:ٯ"y)$:>%(n}X'p[ȴ ^˒4kƓmzDx \ 'NqamP7nyN݅=j7%McSڵj%STy qXymvCg{w/w=wSW5r̹u erծˊsOm=DhEҚRb#n)QOxtվQwe]I}wCa'"[ۂ-z}2UuKP$㜉ԧ:mc<Ý>RoL?wu|%ҷ&K y_!y9 ??:tq3(UU-lkS'ɸ@jdzQˬR] EVPW1DJq2n:,c|ǻ̑;y{X,ۂ.u.b˕u.tKBjQ"[S園S`ٮdNبeJ&9Ơ ~0a(Vm٘L+Jr*vڑE( x0+tp˕ n';wm-ޜMOxX>{#2%jgb2M[`K*\5@8l'e=0u+w ֘鳾{y܀:R*Ya]"Ӧ%ktynlۣ65,3gU}{GYrb;ge'TKwǘ.,rpܚV]Tr,!dp /ԺU,xՉ>s׽~W5oTh yx?xrrx?)?ilbT׬,z$Ԏ.UH٠\U1pU:]JwSrGZq8àd驐,N67QYBӢD㏙W!Q25ϸo9ms-7-%3CihO.J鯽-;MZM8ku-7k9S$8]q2E(}bۏI[DKOK}3KUB^u %Y,u.-&f#]'܆o$x`Yu,dzwM;#oKxn;\[d7}Rb+*Y䛂ZuBӱl{j0O̓}LhK;[aֶaGL{Cb#S.T[>߃F]NK"u^LUʐ_ykW?!GRj29͖qa'0[npcDvV)qz9R)PۨM^aJx W] r>];eN3vxdmĘ(5W2K1䪖weF{mE/QP6\u54x5[hۮ-Nk”i[lUgL]J}5 S:EhiUrgHl!ŒJ$pe=q^b͵Q' ?6|R\,JA ڵ"TDꈭ:ymg`B5t%M] <N_zv2_Ortٵ/i/ReӮ*7[qүqEG* m"[I:6e^p"I$jԴęh!m)]GZkcjS!{e^z}+Cѥ9;R|/ֱeiUԏCNu2Zhcٗg$ݭwvr P8*7/Lk~I'Km1+MW%Bk|oOm>-#qj*|Dbѱkn|n{v#jĮqNpMIUm(7Liz;{ҜݞڝVƚVϬ+sO!OstGvxӉ']uӎ4g_ 1^-8ۦ k!)Ύ5O;YSB#2Zzχ;<.ֵOtge~.(RC#wFZeGZٸ6FFJ4e2ˇpJT$[wgV)q6muDGJ56q\I!̗ y/I~RtJ9kJ]Iy*'FN0s.[l!fw'y(7$œ WƫgyΙdMEU JQJv̋vmrۖ.jWR_M֨djYgSj0^\y'EoECjm$ IƩK>Z28J2TiJ2N#}.s cArl嫶nB.FIJ.)۔\ZiM>/hLĸ=C1s[?YMqp|94- 鮝𦔽/k^#NT(Y LS$6˩}{;5 )B۷W$qpN)qqoot}ZDVә;7TiK|6f3h$dԄ}fqݡ>Nb򗉉+ͶO]>ߡ_VtYf79ڰիF sq~prս|QM)g%l0ocJȨHz V;Bb/kLAcfPJ,ԭ{ƍgpjNR6VSI*$!yV足jᇑ.](EܣqM\qJ2eZT).<9UB/(B0j)mtKEj#׿fDI-=rZړj|'Nڤ]k*i$5qt"ݙPM6E4ke^Z8ۏhz$Q(R Ay2zfRñnpnkbkI:=j &ΝșW?׵d{+ύM'??XqeeĽ.[o=UxFS=ӷdZwenՄ]_X=ĭVa* pKs0ބۍfJ3 gz̚i|wnxtjc¼5${(1fXQ65ȼb̶Zkn>%FQMJXӡ{TZEVNᖣimT/37cNJUPnP҂ZOE~"-Rc4^b- FEͧtf5[)S!OZIښݲ͑;tvܡ+N)AR=hCNn;wL16-:特7M$=Tҕ-.R[HٷnXk sn[ҞD-0WS9p9:-Ϸ-jѬNu{ҹfv)[Ľvwfg(ٷfe+0mYj8Q1\ݧg]Eǎvڿc!4#j5̋C2"}BRriFp7=ô\TZ:\BLfj#I22װ<;صZl j 6:l"6]۸ K'6RTѯ^ئOԓV\?$x7s#r:Oh{ց=MmuHԷd{pN /܅:UE#Yy+(SgQ(Щ)RHzw>^Ѿݻ>mK&^ '$Jۻ&w%F|xfz%˳ L~3N?Cy9 v w/{ƿ kz3x> sXv}vP"@WyC z`'톽Dw%-tt yVY\wmuPYQA0iG-2JP,6/gˢ]u.-n!Zw.N7Q]Df}Q0({a\@=i_X7gFǘ8^⻲}G MZ1)WEfO12G+=-B@z\`||w6ċj߬m}UwRox֢I &c~XGP6Qndpvܻul'V7^FJt^{b^B(L~sѣ6@߿^xqU!ڙ5|Vpvef-uӥ^3  FSDɯKD%0r}FF穛r7 +o"V8tv̖NQU!5uFd"bCr^bJ=֤fM#ʳԷP0O-9xRBm\=`r-:;~3Tl(nXtXi%2Vٛ#vwqƴ`L@"H‹qW.j,JM5B[)WܺUeZFqc'V˷1W7V̾-MHФwn8N;HPSdݷC7&2j.W\τGŎ'Vb]c.x+Rx1%C2T{myg[qU|+m:M:շ8҉yWd)ՋWS%%:iqlʹmGwݹ WnNŤѩ5(9hTٵDdGUi-)vSs2 2{OnT$Xck n:¶(lASLeȔBjμPpTb2~N2~%^k[ܗ[Jzs0ӓHBKq[}JَA-$dFQgjxxFv4r/x*Rm% `4J(&iv7SkԲmSH1YWmx 8n.k']:Z˭_W >ڃXЩ. jTq%Aā[E}amc]D:rmHRiu:uӚӢ\p(5-q%e)(۬ҖȽIf<߽pr&ݫVfY91q2ĭEQgYbTGQ&,yL+N$[q*RVۉQ=FuTܻ>f>f㋳8N6$܌n)9&»iˤsX,݅܍ȩv+sRTpO}d?Wn/Inpȸ%O]StQO|v5\}7Zwb.AIVK^:wb{[uݯcytO߶S<{8KSRׁH̏N7ۚ[xkwYy_'ZӵF+>쌛ZUĦreE9F[24De{}@:ExWs-\ǻ7K-\JNvEk%:s˙#κ].oͳ;լ7wB6nwu:$L; DkI#Wz.:Xp(˅v$Sq,wn\qIN-e<5Oe+vuYTpcojUI_ާP8 O 7&VL8z$_B-H-[uh]T{|8=qVRN-:Ij:7PUtXϷmy鉿:RIM~33ӸS2#׳GdŲ5+/Bx{(WzȨ5Y㞎#|˖+ ط.|e<o/rߔX>7s}VE.OVti׽ .5nNJO"95{#q}Ay9do]R"M6z\tnNS-D!@3N_jicWsy*5uٮRcWv/.,j}=S)j5C^> Ie =gu9ӛqjtz]۪TMoߧI!Ǧ¶m:,"[L!{qAv-o 3{"KʼnrIkfٶj2ƙ؄S`7` k6jzޞ?e5G&6uʷ2%ԒRKE*G\Npom F/V |C0.q_eenƣ<5Oh'67ɪn[SĽ{ڔjǘzs;~׌(ۂ`ܢ1ƣ` _l9Va6%UQWh~P~\F^ZHR@:ۧCJ{ôGeBh;~ۧnU J\O+n2 RҠ)ng}Kh{5+S×ܛ.1ZjG)iRȤIN 4%{oΜ/eO[Nffd ĹK?nnԼMqX'܌nZvq<ķbFnͪaQ`5 s,M_լ?-@_{w{ӺձJ}GF[%v\5[ŒGkOw/ΜM9rjË%2+rd~+󲕛C9U۳r[aJǭm|˒LAʨSCq[XMۺoubfp:t+ΤĻo ][ zt-*67kvS7D·MMCQXm;)܎n_h%]4ܙnRk!]ڵsDUF"`R, &#R_*[z*ZqFXɻ]7|۵w+'pFDەs=r./ᐚm3Hשy yD"jHCr':sA65نѮ^o1V/ f;nFr3VM)e*- s D'H݅fӧ\*޷[k<7u<-]֍Q8R h|p=WlW3s%Q %3l}@U-K6f-NϿu|ڴmWN׮[׸F*mW\%r! C78:޳vBG7ŵ.JթԚ2x)ST!řn~9 W:Wpܢ件{xf8ٳwKE ҰWxVB\qBZ 2wMb[lGSnyԚ~z9ZmያvoN2Afnݽjf>)j3 !;gOYʹK" Wftڎ+׭b*2ϻK>ۢӱeyԪXISUm[z+ugX%0lϏnvg!;t{BqPj>PyvR7Cj]O%+ݲ :qiMj6W}3vC/R=4Som]ŗ=ю, TF6U_-\6MyskwMr&Q\wjKܩyMϣUj0*}RZܷSdY3>Zjqj6TgzpA/M`/Cmл,޻feE[/+uk^Vs1W$G(JsW2ٰu*߻q*Y޵.Wi:ur5T),=0uRmho.twܖiYwrWHntvEj8qhf`Ͻpf(R&>Ki%I7$QӖm-2 ~yߗQ-앑/ x[k8nw.c㩵k}]FkbJl:{.(˩n0Hqvαp7 귎.Gupx[N`Yq'+ruU7[ү+>!xrȫoSo]OC# d^Q]\>!ƛGw^Mx"-+%vdX-:M2UR%d>%l ioSu6lsj7D P>XxHz Ukà(n^Q V>5cVtWj SEiJdznyej[lE' 3kuٌNn4JW)gB {4 j6&]' m-(ZMEz8cz>WZ6#7+[,MR-Z!4ܓtCyE|umj1ƽvƷV\;%>Q :#Le(iVz5 4ũۤUWxX ^(ҔsլB2w-V ^R+; ˂M\z+Uwr+RWY⺧~ Q*JcYSNSλUd8in=v K낫k\IRרSUaCFmϿ5̗P|u ZTԕ}>oYѲ1sfP+sQkX8Gb~6r,s>^\,mGL+7[n-E\.Fqḕcl*Jmjb5 ,m]c}NXfeVlǸJ5eˡ$4%g~N p4Y*WwW٧<8v#;qԩTut,m"#Y D\5V`\\Lȋ];LȇiS6ϝZ l>LruR\v=ǘϔDg=ԈdFZ+M{=|,[;0>RiSi4,S5}yxw&(E7&fݙ4UՕ! ~'Id)]ǽu2K-fޭ \08Vڅ쓬=Vy^^ IhyKR-B#Ըr=]mܻӾ'*Umkoy rTqT_i,/8Q^<ݤ|4ԻO(܄"'5N~#m.(Ҿ2i6Uev&I*<}҄$eNtÛzyWJubW^iBW.܅Wڮg]irO6Ve90sgv.+sV޿aޔ[p?3q*FutUo*eL\KM'EG*ZcAFfG5J 5jj=MJ3OK:k˝'NMB7m3uFҕ\-Ywg%PRqMIyZGY9|μvn߻5cWݷa^+X֥vnݘ\v7m>Fgzv"-;Ew֝}1|RjN𿊀7g#֟*GQQ|#/bo]p$>_Un9гUbn9׃ErQBU-^vDmVh'<R[fdHT]*~}3j;nvjc7s-rӳ Y8[n[1pJx kX[Jk9Mn!_Nю6x:iZ˦U |߉^Ԛ݃hYxk &U^bwKk.[jE+P(˞=9j@snCv7%c_7=xǁ<l {t'酚+1F‹l׭:ݻILruǶkL-L(K0L1&>wXB(pm;1fpnlp֓%Skidkt(U +xulo'/ڕeN r=^pZZ:Pnj8Hf"48ijY[ N[yZٻ+=  ø:3 ?^ܷ^Sr#YK[UF?CuhC b]GM')mڏsNrܗI]ljq6VB. W,UK"YX5{c >Iqā> T:n!,5l2VzCl|+I[*SrjnS6٨y+x,@>П.g+!rn9>N|W>OZT_ut Y""v7|sfި;Pclm EùN,{'fNT%U&LfH8~1v>Il}统u6P˗c(WV~H^bMU.o*oOF0N:_:6Smr_.b+|ݶYY غF,mwjv>f*>QM뭱Sd:`N{l/⎱;n-z~"Gze퇎J5S KG9!Gn;N1 ݎ h6m|S?ɂ5'WOÞ 7|7^ao @mxGmi^jϽ>01Mf0լD3-2T. VXR"ɥV Kl J O7|u?bvа;6.eߓ|[1bmRr,eRz`z 6܎-ͨku͹Fː dPhYgZUj}nvX;z=gVեTv_J }\1n7w2J?ޘγc\E 1Aޑzq;\r]]\Y&[nsNei\uURje*Qk2CSl*xJz-xٶlm+|UjUؓ`Ladqiĩ!Gd\W~fz;Tn*PdRM&T4`չSWq5k훶(N"Ӎ% V]֦wb.nUO!u*J&Oӕ2e|Z=eV쫚΅g#+/RW:طnbi*Wyo)p{:ETKؚR(RY+r웓r(IF) VmȵNB:h Q1ғ|u8E]{,'$-TR[j49l*3"I鯴zhd>Q+\BkNF=.$ZR4Nwհ(IpNi.(Gi33#33e$FXK*NdWrud[r{xnk$v2ıh+J1TQ[#JQl[tRO]LHKٮ NӍnF񨔤֞Em'MILB"ԋ%dBŋ+p̿_17jzT~4pc Vo\ƹb9Rq-'1j;8ܗ)hE%DZKS<璸Bu*%*Yw5ڻ9ۣ^z4U; Ñk\U(o~G?VUĎ:?P?_F_Kߤ~ᓾI |pr.Ok\SklRhҪz{­P .}SktZ7UQ4ڌIM8̈eaӊJZ%FFZu,KZvln廐SNFIVtuNi?CM5]+Ph,{jN JSR$IS^tSUVrORYu.9WyP6 [Kiu m!X|]Y79ӄ)\ģ)pbڳr%*&ꑶ_-H*dzk)1 V3')UAϹٶWRxe'պn۫h7AR9 EAJeGLms!%D| A 5]/Q3eb̄vnVn%za\m kZnv([emqrIҕij|""><hjJשvvǕ|Pޟs}V~2&Z?+2N&Z4w@)4iSڪ_>/JN9Hiۏuf8'It[ȲR.hZ$ȋ_Y ~U<UUO*6b)Ovzڜj\R̋.$FsQuҊj^נ䈈y<zZIuP[}Qm=C?zN(Exqu/kn S-FzKZzOסӽjJ\)F3b!r5ٝ|;6 o=-3*λ]αb\abqRi-w޵⦪~b8Kpo)Z=>)ғ"5/GTZLE-輵f7ݘ۹~+&+w/7GFI:l33fg.N~۲\2|*cnermnnM+Fq"ѪIz%j =YW8@~gc/~?N'?)«qȸs➟n=k" X“m֮VreMh2[uݖ] *FܖN)MȐ`f0 g,C9̑o;ddudJ=In13:ݒvvdMUEJLp^,6t-@͐9'{7m{-3,>hnF;ѰM)->>+Ěz!R* :`e--m7nB\u{b U>[8֪]6^ߤLʦ\DFNo$$dͶlgno8OrsQ\l̯hRo8tuNo+ CTxu!2[>ctFpeޓƻֶR"3QrQuOѳgwQr;S~)6HhZw/GgVTmUf_yt7%$];zLWF̰xy2Ʉu!MCmš_0[W6jf#a-KLi+3Q7c^qg%s<1aYIQeZf+}>;S6L0]Yu_h9߻<ƅpmiM$AVvŚ,*#t2.8Y)-Zhshü97/#Oro"u^/uFgWɺ,p:6a,^x%$Yve^3PƗMnTP&yS}OJ '덫MH^:rXԴJۋ/rI;S*,+yz1hv)Qw^ڍJ2oL׊q(\fDj:^T%vOadɂnS}ZO)N*λdaȜkG_PIEO}нa(^iQX᯦-7^)%g'SJx(.S9zVɴZ{E ))ۅi/s7 VIV-|sj0*UBTHIqRf>FP$KqN0 R̻8j\GcC}IUz\i 6F)Q{Gҧ3qSzKj-Az VЛS-zy:8*mNk|D鿓ND2u+0Yŝ7kqm·?8Ib]u>˗^_>(]vӋzv+ݩ){vZrJ2RQ몋C$z [,pp,8mڊbR]Il .f~d/ݓs㓓mͶ{mgjQwn=Oic9ܚm4Q/6ݨ[TƧ?nԶoytf{@AzT{e{[O'ZRZt~AGD?s3􌿂ՉIw'|~U\ w~di:Kޱ)U/sU%njѩ&GSP^ǝd)..!^U` 1wX[aԇSxoFV6_扐)T 2Mfd=ۖͭiZ7KK Bi9%7@<3<ճԻU,},a}FRqɛr i@ONJvK KLN M, ʖv0n-]DwlI-X6ܶ$Jʴh5O+mOI+Ra瞠\ MG7BفjYo1#͖0V`Ѱ2M?c8>-Crt*JkIGS:e#hPKx[鱼>{5m;wcն&>j-M֥^َ) 6yȜl_w{-ō̱r> U=]iw3)r*]:K]6BdCTZ|>gf}LW}[$'Y5 &c -j.z6R 67MԷFMnÌwI7w5E}o޽+K ֵy4܌ȥW"COyR[q5Ӱ͙f[v"_#q{MV6܍3"u9BK(41ӯqˇc${ߝCi6I(OmθzҜ5k^:>Jzw.>qV8{vU[ڶEm|DžBz].KHjI]x;Mɗ{m,qZXr忇2u^RO2Z}ZێS[2Jen!*NDcrBUً4<ǼMҲs1Zw57c3&ĖڻzmP*FuJG1-dN:|OU}ҵgi2t~F^^Z.VxjvŧnNNh<:]^~NN+ge^g.SԔGFe߯'[vn'(ScJ]kܗ7eJOlRrfziݮq̋S"\*U<*W]k$FջV}? 7g#֟*GQQ|#/bo]p$>_Un9;l S VvQU%OLU{οmU6bZ1MTx%!֙Q7, J=!3 ;Q,ڌ;6ͱ݅q^&ߔ·n #WbwӖX.HtG)N&d̵zpI,n cu ޖUj+VXUp[w]N o.J6Z8Ts&utxln;~HPHS/xw`G\ʡ¿rj Z^vt"[L:SD\h0sUwR,}[x^X,R2Vn< ]2YDr[SRKs8tXb̷G?Ps Tv 3be,zVz D[/I.KOEQrm'$7|[J>r S`5յwT#\w1FTz\Ԛ &"ׅhSHrD\'r]~/>p;:Piuu:"9ő=tTaS7V2rӷk7mb[^WmPp*[y.Þ6f]cizJCgRR@UVl큝.WJP1N{/\whZ ػϧӱE7|E֫Sί.x-Y&pi%v''-x6r'Ws*6=DwwUu]=C?MK [yrtܒG$!WGqJ*%SAz ED[^)/tė/g=#Omd.|^n/sl׉g DZqemqowݮRzUܜ=ڽ-o/Iۖ;qVʘgPp|mm;6zGl9.8pwWgsJ2qPbe}}UpNjٯ}7TMQKrؽtEx%v w߾8%|j;~|}pK]ơ/ w߾8%|j;~|}pK]ơ/ w&~e_H 8PL7:%ʭ5Kw&U2vwR_+rm'}C7#rWoO&HoG?M$UR7{FU]u ;# !Wk`|W>׹潇9Vn)6)*ҹ{%qV4q>W1vi#T"Qk&GwxcJBJ- Ϸ^ˁxkU}ԣ/3.;]J=<*)cS)ROK9H=,r zX @)cS)Da^ԽQ gxJI=w֣gf*TRj

2 Department of Aeronautics, Mechanical and Electronic Convergence Engineering, Graduate School, Kumoh National Institute of Technology JFIFddDuckydqhttp://ns.adobe.com/xap/1.0/ Adobed     ! 1AQa"q 2#w8B36v7XRr$9bCt%u&Ws'(xy4T5fH  !1AQaq"2B Rbr#u67Ѳ3sTt5v8Sc$4ĂCÔ%UӅFV ?_Aנj- H>>,m*>fzp"TrKkr^r.|_&]|*vPuܶvoQ1mwVJUhu-I"=LniAƕ8"۲ k*ҿ[yu:.vUQ+)%F DHyVBk>Hy8jݹ q~9D4KRmzQ)^ʔ.J%k_tVi5NTjg!'ky|5asOȻ)R۸ߩFMԿ3L4j6dڜ#NIwUF]JqB/(FafJRzq3\G՛ ?~\ 6)6W4m[O^L0E&rRMض*C .]Unl-1 1r#Rj/&QɈ׉˩s6Rj=5Tg.y.·Pӡ:JJS:C8-2u]d&vUz;7p9 5VnL֢"y)">iי(IDDd| Yj0; LRfS:ktYK%*N2^m|&dğth":ey)uPQZW)gcC3Pv&MMWd&Ŵ۲mvTRoժM03*F3Yd6\8,\hݻ kߔi<k NTwSԪmljj[>->ptU%'LR>&EBH$MQAUx[$Z6vi&_a.KIQ{hyƒ j"JOC9eFҝfj;˚Ω<[3_m% lQ@4g=5$(J]Yc-OMq<Ǎ wSzڗ)k$7VIP붾ͯnV+卵*t]iЎD31~SA1éC2u)ʼnQn-Uoi3:grI8ؓWm*G zܕ)ZקJ}Y YlGeJ6cB2I NS3Q>k=KTBT]W6+SOXQgGR? telˊ%-Re\hѯ2TF"C/OJΩ6r[N.0{SpljjX1“jOsӥ;ҭhe}xu`Ք&.)yO̒ Fߑ.$Qw;9Iw2o+RVJMSOj[SoҌZ%;`d$blQ{Ro{Imڌ>3egf\O֝Uzx"䢸g+mv%Gʆ:|V[N'&ס-ޝ'kfE|K,G&˳98Juin/\\Qݿ̋v~Ǩ!rtWU d|E߫R4d}.qPw*Ӭv5YEcn~f5c%MTMkb-F>5JT,})QHg%{("ӔȸWMsYyWNRrkkJr0XドnͫT}r-jj,Ŕʍ\Q2Ri>v$5!]"JB2WɅ)]VԜUc8i|.jeRO6^V.¸ Q&#|ܶ-*uOG%JAtRZRr]FFG\۩w+?'zչSѧt jz>KW&ot{7P&2D;&\\>Q2JzܗAKSfeNn[jRrԕf6,q,F1tRfԗ>vֶևj-&R'Zi2=xv~Elbsvm8=ӛ"ū񕜈BȩlWau[]ٷBߨF~J!|Ipr3R̴#Yp)={7:G{+:\W}n|Q#%)7^-h"Ƒq:M*%J&$T軨I333׎g_- ucBwwjp[6i25$̏bU’ٱRv?G\~#Iͪb7<<}Ezt" q_Inw,7-d,G÷%T* Wg1"䥱kq/A.,_KhqŒxwvo u2ۥۧ.bQ}XκA$֣ +K״ZUNmڸII{.v{5z5ѮRme[moyƾd~cRݾK'j.\i&/S6f|b=5: p!6i_ 4j6=.si˧eƾtS^c.Y^RJVS-Vi3,esi08?H$GvZgg?gi䤟2adw릿:"۪lkSN>q-4kI܋ێe̊qۅgDoѨ9; #T.Q;7#~_Ufstb_'w~Xw1Xk,vcOt._}v}8"(4Z\ۘgk?J?bm_c!g{HZV]Fkk%~gEt)b秴vΰB|꽸}mp~E6ݹv;7P٤v+ri*3Ԣ|'O14_~7nP{7ZU\Vű[ +7󖱅o#:ǥŬ\|3r%TJX]V7ez¨Y]lc|O3V! R zbJ'PnGqVJ"19WVeOF埜EaEJωqCN5Z g-9[S<$sUK5b|7sn\7x qmv##FF\ w[=-43$^ooVSiXօv7iB۴yg>]Vf"r$J3""32!Zh[K%7GvNLs+4nB/B{vlsobJaҺJR:0g%&zR\ S3T[&ִor*ⷳc3ʊO[iozW٨%$gn:ܶWwFBԹjHP&z u&F2\f;ipW73 [; '_̽b;vib!oec dC-tS__$Xs]l9&z$2/N>%'[}b{h/{`{Ji׉׏ YJB/X%}.|+{(S:qz]4_Kѵo`^tY_4S#* ^zvݾMr+TrkQ g.8Ͽ^i>ӈǙvix>$o( ^qt*&t1oJVu-ql5U6jCЉmĻ*"?JT=K'O/|=Vo}l0b}}f?X[?/\JSBe,kP8ETJ==?.p5ފgbU9}ǶdNKk—_$8̸͓ۍ8Di\BԿ-1v{FF]|.^ۅ{vl12׏z7-R7wE?\nh\jN/Kձr_oBw"N QMBZqe-m:ӨSn6j4%!hQ;sv'm4kcM=!8\m[M4{SMliۇ%eֽR&N:{2A8)THLK3Zj[jPBx#BگMf:G1\`edcʮ?|w(-̮vXt,bW2;.ιNHRR#YwTM"<;mk\.foIDjmlJ;vxy7o7i\,KQŊ9d^Mmgc L*.T6tLeIuOH3SJQ3=F/ʿ<9\JM6mN6=<{xkP!F1QR[I$6ُimXu2An2yԒMU q f[IB-'䤯jYm52&JG\zд\~vdg QtHGXw&1Lw+nDEdC1w|YJmvP)HZ>i0BPβә?R:QO["]I_Jʏۍ>QKyu^bycBq4lXF~l [\*N>-J6,Gq(Zr5h]CwYӤU~ʶߑ u*SIv%ZfJ7)! FS*s_\|IŸZ)J ]ܜi4"z[+Z,MOZ))}|Ʀ(RUNIII.S'ˍO~˨rn}M)xxӕ0 eyҵ7YMAB]ӣU:/ѭ*6bcwP͵ "+qēVjŹO|GtY4V j[mLV M -m>",B$ GD1~j6O4|LxnNmqATNR3ε|DŽa[fmn-ڭ+FiK7Pcm;r5 l8r{#-]'nrFh2ruycb;pW=njRqRJ(d mnpckNnʹ+6]tz~E=ʕ l ZZ5jSi3#47.Lcfe`9؏v囜.F\-UZ:*0_<Νu9Lӵm&)_3\^ҹ3"1n1v_|uRʞͫr'iȧN_kH׺8xXrj=\МH)V\ˬ.Xʸ oVRC}ySU9/OBY먌5 ٿwޞ)rw8Ӫi5*5ZΗcGƱ !ZۄlmpjJ -l <R̵/JAպZuq\IdUS 48wXJJtcg4cI~aqߓwŷrm-v)G7yS^7H^-\mŌAq|"m9IBnF㏉9[N+mmy/!KKۉ%n +BdddfFF6FQRN-U5;Sv'm4kcM=Mn)\qιqUd9F%",6MGdT%-+~ f%+y֛^3SrF>6lc(֪vۊN;g._0Sѧ]ETWرkQKzGe9ʨsKA"yC y2\[5 rԭ7Gk5Mzw_4sM3hxЊ'oÍ5jsub )ͪ~tR2H]R͍>̋m6=%(˿(Wrr-܅y5(ܔJ޺YunW̹븹NsqK ]/QR#"ZMDfD|43Qw|._ԡSqTZBg??O Ϥ)/E_U|i}2 9Z?¹0:x'3,whǣ?C y-A~=daJј&M?D1_PS+Oi&;a @;Dž7[ zZC"bv:jjMQk$M RԸ3uA\=wI.AwC"^.{?-\NSiˏ"b}T/}q/ o.1M}R%:-ZniʒL$SgrBW*,Mw'N\ɇ{s\j]VryG'8f`}'N<*/`U숻z CwHq18J+vԕKss4R53/&XTt1bZƟo\=%nO)h$rBi-nKĪ^ ջڜlwkYm[̑+/QrZo%TQ;TLs($2C:s.%+eoNttq۰kK7O0m_t_pZ1SsSM7"mevFZ[w -FJ*T*jФQRg BSu|]g:ɵzjqwmltL.e3sRMچkSmjkmWœިm++¦'tILk*բQ D,PB\lI[9{%Gb R6öۍmX-MaʉA931cs..G4CujQտ[9 }G-xwl)IQz j Ó"rqe&=]꾧֎c)<kӳ+0JrRR3'TnXi^xMF Bު*tIL.[h"2"nKzZe'ZV/RrNYz]8죝n]Ķܩ>^Ժ]u-7^\mZjܣ9+Rmn ߑv?oꋘ?&ƪy^N4o=3-ؔ̿*`}V݁ ƒPu8%$ ݗ]wt;\y\>='OjPIp/nJU8{϶FNMsf"ίNqƹ(+ ݮF2Km |jܴZs%zf*eȫ?]4)I۵nR&FX + [jDh(#哑9q9Eծj8noǕZf\J-l&Z˫}`ӎhyrΉn\űn]9pʌӣ"׮Wt?N4_I_~54#/my1Xr*척aS#DT >q ssΛW;3oUaJSRMDgQnt:Ql,/ ܷfRqiM Ȼ>Cob;A>ڦWقM9X~/!'MW.}Vrߔꔵ!5|iB(0-zF=}okڢE$^wW~nokY߮\6՜̌{i-AF*9)\t9IV6۸5ZUF6R$ŨQIq砳YUZ]eyv >hI櫥N )&l JulwE1GDOuFN2| }馥uC1rޫV+^gdb&W[4<^e4YW,d|htͮsUM)۸8:{3d{AѢ)~ \#J=NdƮꮓ90 |1K$v*?мS ]i$J,C,SG?/_՜pMSƯM|mG1V1$~K>CSvkuj=&) -,yLjuFHK{c駗.SOua;BrSqj-ۍZ#'Jys7[g2z/.u4+XV2VQ.ޕ)$"(%)#Z7suZ%j }BǬݕe)Jvz8zJf:hIN|svO1O#IEcۍjݽ:SdὮvu^@:o^5cs>i/VqmVm]ؔܢn6'vޑ̗J4Wn@OlKbX ;n:hgJ9ŻyǑz8f܌q&Y fN0N;[69 rbׅC2/#kE l&2~èMR.*%g=Ft.%؝e8<.e=Uv{~㻏"EˑnvDѭ͜Lu3u0:U֝$[M5<:oi+V4V9 6nXvx&_ q Qqw3W:uϔ2yb/(ɳ|5zQiJ#r|Hw#.W?4aDŲ\ugWG;Cw鐢K|xg)##=O.dF˟jMUvWĻsr.z]kPc9"]R)mkfOd*uYf١RsB Aîh=k]ʳUrrZsq`d#r$/Ը3o^&lRWȍyuW̦Y4QDUMJ65ƒ[+ygk XK_±k#y:8(TJOSQhJt2.DR}"5[) r)6V6u5k:eXZmv𭤔!푊Q[qQ}ҹLE- 8qIZG|UM4j}Mܕ[Vwm{} Naqµ"ԈM zOpKѰ?IAD3Ir0'/q1itoB5{%wkOBn-ۜduqIzYK60{+DʕܞqIt";r1mG/\/ym[6JƫR \L=S=OT@Ix[TMm{>ݾտ֒ݸӉLYIx>+"JVNzx||5rI?C{oz8۹e\R-^\A2F R+N9 vlT]"ۭ d)t֞i #E2jB@׵=#/N+!ĕhx}I!cM`ąZ*ŻɄҒ߮Y.Z}='/oۙ3IpW̮hT7cTSuz9>B}΄&h!>lӵn~j˅IvU.'v'CSZw8QK3G> ,J59ٷ+HSg䧎hJdzvwv-cvxS5[̊n~ؿ%ַX?O0\6ne 6kn9.ϯ} *h 8_QhLݣ7q +=XBҲ5?[[)+F`=4 }B,sNg==u*Nj9k_GJ)+R~GSPBȒZ:(K]heL=vKPӢwq(NrG^ثϣ?#tC?.ͼ[ۅo؞y#%ǛjVyLSw%T*s92JTM%"YkQО.q)gCͲn8cgi6j1MѾ[{9h^vƘǚםidfi.^RHmg&rׇz:}݃}xT$ضk'5s-狶,\vpbPD،=Okf.c#cdz2FK5T!&)|ntD<+OŹU i-G[EE*FDfeaf2QƤM\UG_{ǹm%\yrGy:.\4wjPGUJޕUV7Do\7Vy_13w;[?c]H\$IJ,*L]3b%L{y.JRKG2sq,B6T}(#nW|km+q5] r㪍bJ@y{byz,b踊3ϻJ,'^xd،)JVw#.Vټc''ÝպWtbRؒJz۠8!o9IۄS95E9ؔ-e9JR{dmnｯ<[~n${~Њ$W?&ՐY_? #a.ߑv?oꋘ?&ơ|y^N4o=3t=~7!/M3>n8W홎2M`Qx+ z qy8%]7_~540ۦ彷]Wq CѡwkďyF5Dum_}~P(5.(X,K9vᯐ?leB9;Jhm#3{CxGE-S{;@Fz˙]=O'!ɿ]' r`:7'2bЖ>Iy,/eTy/V<.H?UYY{\^#ѣr9^7?xoRȆ7EoS_&??zϾM?(~Q-K&>"~aߨ t7Emsϛ+?;fCr)fY+>z$tIkjn_>vnrֳki-˹l= t;'EyC¥|/BLwBJdgjۛ$s S1|ɍV%JI6KvəhzIlBYɒ|0"Sy0F>eo5W)O+X˻u';v)2vVq۳kۮws?UʑBǴYO漪e2MIjPAک\b1)DDؚKm6ZWΨgȕ۶yjڳ 2ضN[C[|r@9Jfo<_eI7q.|cÊV߷:i.:$ȋ)1%%)ADZCEBxJ0MJۥy(bNsKM9k43IwNt.\%N簤I'.j|ƃ2$grBEٌ\}9:v*!n7M(ɽ]7c@XxƱԨ37īf62cTTfFK]9wntQHͮvٱI/f|j=7}\_V5U^+:uljSȃY(XI.ȱmo1甅jڎIZ2>#\*:gY|4k\8ZwSqtyA!+];бޞKծË¥e)#5ap.QK^8VdU{*ѽL\=qmjnB5>{ Ӟ`v±5 ^k&O~Oshɷ,;6nOW>u6{RqS`)S%jp\ipdEBLfTWy$GIYw~䲭J.1vSY5z.V>^+Ǎvc.I[R{QsNR3ӎfhd>y?UJ*}~[e\i5U^͛E]G_FS(Iɿ]i8:4zj~շsW,ˆsy:%O}iur]iF5~3M:Ӟ#N06)4ߧgdawIotiz:1r5YDZLHBSi;NQc44la=Y kQIT*ըl:tq2(է9VO4뒳܂~2rq'nrVZŦ[t7\oլfb/mlpc.I8콚q^1iE~䰳mi[dۧw֤ICfdFeCsg:i| 6擣׋* 96lust^{%99UNRvaMܽo ammi$em4D6DD\nA%$$#}۷/ݕr99JMն[oT޲E"KTaP+HGkŴj5TM5xƱOS-k`ۛkٝWz;{kS}F;~q|~^_|euwnE'pSupUP)V]vE+t =ZRaVdG6= *.ϼnj9:UɷbېmF_tޫgHjVS'śǕًdkkѻ_]Kv?nT>)^e=Ar1'3ԔILyD?:-^in):{7.؂\.:V }#뺾.3r̸*xbFM aȵz 6SQ:ײj[ 8nn iFMw rR"5M5I旘35f^j='j:nNW.ʭocZvZKV^ɚJ.cM1ZI7E'6rg탸5oZ=[m Z`\hbMUR١Ȗĉ):Jin!_7Dй+f̷eKҷvͨBPR(V`y6tw*MRΝcB.ڭTnc;P$8nFvm4(D(R#R-L -2:FP lxZKQc6I("Km%$E, 78uXIFA$RQI$JbInG]c[ֹ:ZM+n^')JmJMJRu{e)7jQDw~%yQl}BZujSSf۩QZ+Dzhd5o%BIc'GZ?}΍:>Ɵivז-%݌J5MqGWTVʦh݇ܟ~Օ_6 n'{3~mϬj'J11OȻn߃r Qr\3y٘+WӍ'WxEs^O3 o~[|7>]]H9݇ZomT@]?5B:Z߂'`V_+/MSKX߆ޠk3?o7y:4R/7þ] iG߬aBRU&?r&/} cQߥGj2?C5Yśe7hU=?+ x龳f-܈czW^7p%-(\D4h{UK&ӡn^m]Fݢ:`δvj俜F+) y[{{ 7 tu>gvrěOj'5 iRg[ͶFjGe n~qT$ci ۚ0oԹc*jL[sVWqj\ݻ&6"WoK:cnWmrv)o>66(F>=W^bf#c zzʞtپy%mՉPël e}J.\Zk4ttt>oEM=q)hJjI=ͥ(%]脼_88ф;͛gWG;Cw~˘$4=uWdĜTثNDkiQL9U*O"4XP`02,Ge-k5$h>ܼ]3vr6!9RQPIVSnM(ۓ{>;/Qͱv{3&-[rc)ܚI$n{Sv3[j00)-D3z}MRzVQпj,T[uVs0\}Sid;r(ݝJ>æʺL&c[jPK0~d(FKÝW\m]GTcF|Iׁ)I3~#oX%vҦEݑؼ5Żv2qAZTE^..M{ʐfȏ2##.R}*KʛZz^ӞN*lPťLf\G6[WVQquV]XAi)5J!,$iJ6o$tPZc;Kjx_n3`qIelV~vLy{fn匋Ѿn%;zV.n'-ұdd2߽1bZksPe3TI9)$ԩIN9Vơ\=2885N\ p)/a柛w9g_lױo8ݷ iixJV& ғRi{N^_oAŮE6Y7I$Nk$|Q)-*4Z)^¸%4Qm [I%.c-OV+C֧R#%ѨCe3i;w$G+_dy| Fzj$DI(=OA gj%v/]8qԯNIS*֩',Q%\44ZZ%D|Ǧʴ6&vֵI$%8(ԬƾS&#Z. }6z?b/|Jl{ץv&mpx4Z$”ڝ4-H%dGKfM:sKSRWeJAn]>s6应-W9'H]'uȫYvgK^\czp|My\鏩w/ËQ.)]\QiS`8uL뚛̸=J"ܻi\å'-)54Ue]:K\퓡vK xwBqrH\*֕TnzC.mT=t-H]SČ~Nu╏NÅ3f|͡G~B+Xm[Q7U{9"~jgK Zoʰ7"qJ,ekSeNGgϳ] ^.6:s}_,%eRg<5⿨z{ZPun#jRІ.6g T.!]xa c#jN$Zpl̋H WZu8WmMRýsĮ?Mco~sx TU҆Q :KDG4n42.<3/'^?6/ܠڒ^yrrÿr2\D}}B]^E~^T cɛ7϶Y[<֞[7d}2%QPqOLEQR\CIsj1?\}%tJ0e~ *sk"*)&ۓEi#{1J8Hrt|'ܝRr8)=ƔN'RVz:cf]F7bZyZUȘ4x8,#JG̒?.W9XnO]KO]%]ƻ O5Γ/3qÓj؍/r̺rƵ 5\&m6h.xoeX[=<3%< lZ"2h\Z[&jW3ejm?k&[]ųj+{N{66leu_+lj]q* 7g*knأYv= q ەdxЬZ|%GUrQ3jLŒqET]1% qkXYūYc[7Ś]QY\jko\</Lc7+'hMSUc6qXyؙ~6#ѯv.0$BQi5YyIhɍiy=KD!n3Vm[V%W-B%swa97ajۗ m+9~]fKq|Ddaˑ0A]_v޺mM5* F-BYHJ5}q>ʉ.6hyDmpD׬'-_v5;5[8K[viJ.3dR:oYHHh9I7:۽fi+wm^ [)odPѱ52CZUJicSw\&_s0uBȍh32džzQflcd^m|7GѹE!fO5]]H9݇ZomT@]?5B:Z߂'`V_+/MSKX߆ޠk3?o7y:4R/7þ] iG߬aBRU&?r&/} cQߥGj2?C5Yśe7hU=?+ x龳f-܈czW^7p%5|Y:SJE\U-(a_cƣUǽXXKiȞNlmۊڭڄR!**ܤMeȽ$|X5(Ź\rJ~ܮ]>'HB0cp XFr_c?f?7<ukSgov¥iG>>䙗i.+t+bOjIܶ . i^:nm}s}(3>NZ$2Qg([".>i.ƾ)B̋M8+"- >eE6DݥJnJˣt׻ 5.˅nJGwZD~!i۶a,Db3ZQ3O#KO5/֍ozuK'GbRi᝘NV_ҝcvם ZoX}F6z 7e5_e:ۓj=AB+iܔERadMBq*ԯ DwI/Gy*mĥiRKg6skY/#SN4e$-yXM YL?^ĸNNӪ{$r1JJRSLO]Aqm>V/s[~i/j+m>z}eI"Qvp]{ZԼ:{vPAG2=T͡@ڐ#u"E*>C;o$~C#_d/HBq^YRٽzIKbOm\~żjFFGdiQ(*/i*#.FF]©m=BmpQQQSP&Ҫ!T&^>:y)$ˑÐFčI Bӡ-t!bM WҦŶ'UZ=}zvn~oT/\ǒ'nr8 AJIӆz<^uߖ4eFC1i+v!3qNyߕni?4JZlmYFXFۼO0B\m[ tʄU3s"Sr(NJ;SKW72L4̏BVdf^Ҹj\]ȱ۪(ӷm?J-KEmWڽ^4<8qu%9pŹW~877ܾeVгS(յe^C]yX͹! םm4FGȋ\y'Z FX7e)|Gjt߹#gb\ŧq_([R8[qU$Z (ʻezV2V!iQ,i$JE˂٩ a(GK'O{vnBvryRd-RK4=qxZJMl_CuuIz @Rt㮽޳!|68\-l[џ84-2Pu" RJ_^OL>G1~XnBŬw6J0*Uvlږ1N G1q9IUm*'oWu][&UyYZbBZRZNfEJf"+2nF~Eû7n1xv.RUM$6 lAxSQJ&n5ܞwlEói"#>4׿Q.nEq7Oko[1wg8ZQwZYiqtm&~">Bo?w͡ni2峋NCEy Ҕ+%ZJ ʩq*fpˤl,~^Mχk1+:ݕ z&Y`KLӪУDr3[*Z :(SL&ݻ۬Vqsyԭs x|iI߽zZrg.:mp%6ԜvgmpIUt;QbS.Է) ǨKSV,*lڌ|5Jt3#NP.=+OZ~/G سIgbꥹJnl_DUM\iM!֔wVZuԺ,yV.Q>f v:݇WiaŸN5Ҕ[M7SsrvǣrMW= \8ZW-jsnڕ.ZnF2qt ً[ٻޘY۷Zm"Jxr&NAfA-݌to9s359݆mZ+N1-qS$D=17 x׵+%_ ve4ir6Z$FDڗnFtOr'7'{9C˨ꤡaYoace{Refnft RR"4%ʌm:Sj3)OdInTO>X'vxV#jܮw9Fog;5.~Y5\~18YQܹvj4+~t7S ﬕs %^۵ڴDZV69R^Y+rj$ԇoJKR5wB9C>Y:l+EǎS{ʲ{T6Wi* ^^9k/y/Cs\g*qڵgn4T8mERr|Ti+iPe;;.i\EBEJ 丬i9ɧM-ԼsGDrZ>r#R>~X9y4b棇9JwV۔%m(b[Tjvl}۩~nDԺ{Zo-YuK1vx.nWuO+jN [ٮ0%"΢CdTJK-RަH"$I(*ve &҉FzB,_Vpqp9m8werv')E;o&QE׵^d9˦j\_,ڵugZȻ̧8k+jK{wmr@3ӭ2 wFkzFVqs1؛.v'I%$[iT]D5Dl2 nk7qUxԫLS+sا3/ΖeZYK<["%-g/kRs:f3;*E ت wJ%)5&+&rw*霣i|sMҴ|;R+fm䡩.!**dӶ-6s6,]zAXMWjmnz%SJߴm2UXw7MQ%<!tKys#P,W>s;3IYwx<+i_\\\U6 u7P|xbn_k&ӓVOe䦒 VUr,-㘘"-LZeOSҠթrEvq8Kf%5%&K"#%vD/.ZYYŏ+p$nZkvއuW9㓱Z G wYIFyf)?ƎUm5ԉ/'k84{KO:rQI}XRuԪ|*lu)3qZ[mSm5R3".Xcَ5c®ࢫI*۳~wRϿQWޝ(EJrri&ۥ^ʶ齲Im|[yb;mnm֩uiܘq>E+Ikx߄3r33-5𹻖09ϖ9[Tz~mr5NsWl$oPusޛ^{Z;);sڹf\3oٹZmԉ/'k84{NO:rQIBø8Bݱ3n֤DiK4u& ofSȒܩx<˘|N0Fչ]qsp"}! QWw@t4ӭ+cO5%]'*{eM߲DRO1y*q8w++e!c߶ܪlZWّM欼 CQ̼빶lX{vib/V/ ai;x6~]+z]MWB>re-:lgk}պ!#9?%܋V-c[z!W?c7YNm/jRr[HOzԻefճ0q15Zp#rkQQ0tU-AmڵP/cȕ?0cZYj;:0ZM=D6g ?'UN+ձ[K ܖB2'xq9{|۫N0ku 7xaj;n\ 2[VznMlWiKbSk))f..)Km)&bGZ=>OR܍W:j'rM'wYz&/鶧{Sʵb"vջq[I-ՌZH._x*BagC'T(Q:$ͳQcMCKy?3g'ߝqnT);qs #ؤZ}OOI:cfnc8W~qy.;^pVl]Hԓ>^H^@7-AA܃nmL(uWܻS߿ Td95Bdh4t6*dDh!EhI[iŨ\L.&Nc ܮf^;$R)\rip9I|ٺ?#R.ZDZ;/]nݻqs\QE9M&Bd ]N mN*D>tgbK>+ˏ.!23]BȔR1ɝ^j'k2ƮqBQq[$di]icV/e`޵B.FIIJqbi>Ӥ|p; 6${)RU>_e}^dzdfzi %ekRVUS?6'hׂ)5.\+qUgzE2C˷ecŏ^֔ibk shesFWJ#~> Wk~ݨ}ڶ>ơǚ)׽ZƉo~B-ڼrvoE:Ʃ3ۣK7+Y`WirS):{>ڛ}:wԨ(J_";6R%[u&ƫdZ_\'np| RJwNeTW,=rrbnkڄ[M3ܴz)3- R.?:okۼ0TU'w{6&w7j1z3ON'fGoO?)S_bQ_¿R(^ԴԴG.EtMڇ&RUiW uQjU> Kiu1d<ѥIQ'RQ1:O/lŗᏩiʂv&Jc{D5 Tt)1.n[n۶X}RjqnOʽ(~[Ns{ސ⛌uO,kgo֢dRNQȄ .'6W!׌P朼tdZjFGE"]K@'i۪N;sI[{SOzk>`rRR+!σj8&TjlvA̷Q?HyjyLHNտJMjܶT۽lG?SnKN%<‘ nq[N0Sq[Ta(&t(|HGO~gvkݻTR4&Z$#ViOY1r$6YF?e4U/Mvxų:zbU^gQQ+NW_'4jfz^c'#`rvrڡ(IJ/J ݦ6 ]-CW |_{v*_q3^DZ}Ic6Uڌ8p7{crZq5ki`)mU6|-Z5^iEz3P=:Cu7DF'k%}<C-޹ֲ̱#\,(f88%X-N(ck0VLR~} G"-8ӏ/ϰKq?(#nrVTmZ;zióM4 m |UT'C^_1X.gXM{%ʤd 4\ovN":"y-,T)fLQgۢr=/CƹǨJVr[a+!rT|%Y\ٱzsS>jͱ.oOc6f$q% ǒGo;n[];ߎjrk{~\VۓNIGn:iqxo |~t5)Rxעri{Vi&NUOl_ѮMfsޕkЄay.0P{7N((BaIP$ K"U6Gl ݙqJRu+qN$ m#*p<|{:>-Ev=86N*MM긭U*uѾ?/^o7;'u,h4݌xښRM:5.(/ \իU.{F^rmF-Jɷ.>Q"[4xT^OZ~mK}T0ݛ^SAo9u?lX(' qj%=X}"^e4wˠ|rܫ 6I\Ķ;Ӻw!'ڍWg{ i U_9Avhۣƾ+:vs/MK[ɭīe{`Zgb}r[i'GE2J7Nez579wRq+Un ]J.cJ4M:h箽Wxxm^ pc\wcN%'My $$| :$Fqɏ¾^қP9J6Wxvu}ݵP>Z'FFdg"-; [¢cmWkÎT8nG%ݣ7*\խCLRYZͤiD&J#'ehbSyXK|y*ӞpS̍R`[pTr/Eg)K+92{_ n3zwz'oŸۤ+sOj J:`T>Cf*lwd\fYOP"R E֢̔L4ɥ :;.b(B02rJ蠟9>V'9M%)IqnhP<%,r'P/vNSwr#w"ݨaqc(|{kd=^0jTMR2ULNz|.<|^PfY22##!,K~E BEJۜ&jRNsHަޛg\r,v؜.jK3)[EJ2ii{KEiHP^&]Gn8x=K}Wx/KI9-ϵwQ%spܾ[^R}S3$qvq8M[ ozKxcqmJ/ӿ{_}7&ݨ\f6ZSyQz& 7ۉ[8~UNn|nkiTB+4RI8'Nc%tn{!]Ȋo.nEmʱn𵵥J A+wy#+ikǒڂ;՛s85'KmE:Ђu""Iģ5p=БbTY-ͽڔ詻ngL2Q}$de# fs^o{DUUsfwӶ;s1T,ǤtޒQ\෼J=.tKU,7čJ5 N$y3kdSMQU~mO[03 $zAڟsF5^뜞"Կ QHmrR"ӳηer+ҔZ]hE-6Jmt'ޒ=O[sQj)6K}?e4v_KfZheޓ=BV[bY}lݒTTЬ{ȫvO_qpRApVŗ 6ju=*BR)g "O1yhb=tqJ gtm\b3RY+JQ^Ō֍\յ\>+uSi{=x ^w;uӘ#ĸzLn*$anok߷CBӷ}5Yqvdž<( "_OWit5:EZj2 B ρ1̊fi[n!HQF82q1牙nqnEpT(2RMoM4ϳOu ':֧_Xjsg jP^(ڙ{2%E͖j^}ZU[Q$'U) <܂%!s"m R'G5M0<+zM6qYm$ڕ$3ǧH]?o2N<8F1̻r_my[Rf59NjpzBnl7*{.QP 3N&^BLJPjAHCK2Q}$#~YMq8 k(MFMU)8MEqTy+Tʞ-ar5yܕOXw!e;q-Jqܶ䓊Y:LC UE{/t>r"lI9)3KJjϤA 6SEE$d߇3KG*En|P\ԭTn6I-ƍKTj<1H_zwGr19wF N8ݝ+a9ɫM6mhePi%mmD! """"""*1bRKrD"vnrM۫mmĽm]ӡiG~e"˩ lhRTMk^MX["Jݱk7_ޕ*DqĒ&flՒ}`W}~SմZ{ĕ~wm*/{{ѹ_-0ط#P]xlڱ~Tn5wi*lڪ (JxioϏbqKYR|!|KN53 OS222$jzww%i}>N)E+rۥ7c$Ofl/LNث\6H9: FY󡈾I)fB֔JI_ ֣^: 9mY{66㒢7Uj]:.-os[R&gMF3˸#໹kmjq^8W"PΦURjʄWa˧T!͋ lW48JB2ko+ /Nw QwQzQ ے%$ޓ7^YL|r7!v%Trܥ &|M8~ybrn[RV gSn{{*#2#ԽᢏӴHak" ӌcwҜw&RJ07ױ>Ļ =^ BɆ)v32.M1=#6%̠tҤnzqMwԣ~s*%-j|_m*.Yx9Sz=)qE4 3pk+,`=kNRڥ=B=nŔNAx)Q$ԩȧ4z3t#Z2lҮYn$S%y- JzGpu|LBV7ZW#;Wwipܷ%(6jFG5#{$D"uۭ~]֫SrD܃fҎӾ+Tu>-ZTQ& N|$沸ii>eRWݳu'[O̻j8JۻEѩ[]vni= ڒ,[_%kC7I3Nv$4ɎЈeٸoUu:[}Do5|zNq=Tre%ɧ6&~DȍF]ƞG5q m]/w/ \ʲr8=oʔe9U(W"|S]uZd#?Se[W"ֿh][-7Nu:T=)R}.;ml*5Dlf $fF(̏T hiIUU4Szɕ t(%_|2 ~6eM;TƗK[f&]LK^CE2[ȏBOd;Mi|cx,^6;sیGpQ\NuJIFTJ~đArh* B"$H쉩eXPRj?sl"ԥ)su]xpԴY%VESH"ЋJǰ K&5^Ukzׄ8kEgS2h&Se\ Yl]WҶp-ZUvi7QS:4byqOo+[̺腋[6-_Fo.6[7$p&^ _GZԸߍkc.qqoI[9m߸YxOZЦ1uoiSH)P9Uʄjcq= S>֙NeR><;+ڌk%_qT].srNO?s[=vH[]RZHRMtᩗVؾ:/~u)ԍdg%=edVrISb{6vSu=(ܥ)mTv/J}̇8 S3ad:^hBSf؉OɔLhI_1d8,L><_A0y3rXq"'(۱;mFNII.v5_(^q~X>y{3צ I*Vܛv/jW' T'NR'j%ꔩ:mJ3SB}΋!-H-RJBТQoedi9tjENenPpke.%4]#{:>mkEɱdYWl\\\'nRM4&U>?Ќˉk÷!𴪛]]5}UqG~ݏI"O~s6(Ļ)qO~h}uԕd}Q~G,oE!&G&/]_H-O=o{k\̭bkv.Ô܈+;arZx)m?M\3lU$mk-CFXjTv6u' g:Vn_*qk:VC A%'4JV%EY)#BғO4<e׿jQQ]yUr4=wm[K1r׵%Iũ-O}|kC;/VcݩWZ)EHdžTru]8hgĵ-;=>U_ InvTm_jBM+QiF"9*{DI/iuo(=TzϖmPQl_v4z>T*ȴ>YF;ε\t]EH4ꌇ[VrLzef 2T^V>g2~kg5~Nק;{~Z~W}&ŒBӿS2$J?~(Yœ"˲ߩ\O]: J׉ښT{mmIѩn3˧)4LdFZ/zUG>U> n 5& ϴ-KJi2o]uKljvK3$bԔҚV旧iY5.ίfi96v7!v))FJM4{jG~Jt/lUE%pTAFe4qQk\ve۽/u/Im+W')v{\-E|Pms7߮DZRr۞/mu*1ՙaB܆ -xg3#6ۥtRogʌU)׎]ZҞNnŞr}F1Nnޞ;cZ{N}ۿMiuxʉ*3qi'9KHQ$WJxXyرŔe~[v5~/jN9Q4o6rJv FrdxM*iRjMzUinHdн7ᾞS=S'7 } ̽zt7K|_g J=Lq+/Bw_\ۧx\HJUPzQ<hqF[V0x==CsU7q|^ {)Iq38$_A(VgcKu06Ƅ"%i~_ˉk QCܣB8Ku/񋇵u([w}$F|8TՠI.E !;RJ^}MɒD_q2];Ɖ{5}*n7nEInO{Mwv}&q+v [V}Ĝ@%>#dXQ$f;iep.GquixVt x6bj͵mlKقQ[T]zs/&yەnM'W}!Fp_d^Tu N{ɻ'l{խ2.sTu{W^H&;1s)Pӛ6>$mě;Łnj= fLT)>׸+qReɴ[UR\L*P/!$Ӊ3Q 'K=m~6XqW3^W+ųO_[F$rR*u"T%@O +%# ]˽!aܽz{ͷvQh쩎]hGތ5ɇ*DzJDRNLi 4:{~2FmXY-zzĽ^f=]uū{/+&c:Ma{ĝDp2m܍kHș/(--m_vݮK(V{R}.k&yƴ7i^4@3f sK3^Ř˸B=]?gt5KbZB<e;kQLpxuWC}n 5ҴepB##~q= `x]KWF {GfŲ}?G.I9pjWkU]>={7q{kO/^I3==f1ɏ%nnʫ/Zu_yXN<57ۍ'vy/"8넭M2eԷ&Y,в33%IkjMr7xf nmQkX4踼>a-GcIeތw&U=-:qnW)z¥j :WqSZvԒ#j"KrIU)%qrmRoDGQ~SYRsu*V)  ,/x)MFD6O#]z 96[Ui(JRfw'y$GeUީkdMF-ݻ98F2d[o{Rn0n-xsV6Dh|Eb2E:KCOӪv4SJCr"J!!m,hRLD| ZYFm/X~ΧfrN&4Ƒ=Z9Mh.Mܵw/BdrܥniŪ8ɧ|y%œ[M=_tj?F!z5\evM:\ ~F-sg钬OWq“iiȍ<Gi%%n2rqͻllƑ)okw7}\Uk-:&fj솘XerV9yZuʼşdFC=rmo%~ZN78X(N)_7.Εn1MpJ}62jjJdI";R5&iLԸc:jmqiQj$ujp\{;v5B񥍪Xn Ą4qOERjzN(Ga٠䌡)p*v(J7#ZۻZ8O W uONb+^Qipv9GvֽƼϯrYƖKGJQDNPhRJjᡧC"21"9ѓS1;R_O7/WGz)8fE%F2ukmvSov/iZ&/]~KmI[:^~ͤ\kMi稜\ywJt3W7 8Ʒ~ݥeFgѼw"8VVSج\뻆}ݭ/J6Q)d|)zU3>k\L=;ow֯gN3pKѫ|wmkZ$z^2R:E)f>ς нd|#׆?\ǔpV{;\$ƵE%-ͪm0S6[n< kE[}mvE4DDZ^$OZ0*$~XUv҅B@^?]so#%ojw;Y#SxxueBگy v^i-)s)zV jC{7Gt.w3v,ygg8s]aE_,*E tY5k٨h=o"m泏:\6w噓aiL׎n^c\75AGkЯ0Lf46َ`egZ˓p/k;̛]kq!ݸzpԭG"}R9Ve>ˏHUjJ-&7nrnwG*Xv\˱/vN}O)ʼn&CV͍f̵]r\PMB-6Du-#RͰtRN^)mT _}nSȕC*_xBuTkJW[`ɩ`ejvsngP ڻ.-WUtܑqԹQj)t;vN&RNũT+8%IXӃ5fK՛-d9 ]CƑm|nZ-6=Hz,*aEm W3VzRšdY~Xf׀Xx"]s;)5u*ُHB BRGS6bݶؿ 9j[1*jױga7oX CUI%0v#~\-O-Ꙛuɷ쏪&5mY٦M`LJ2qK~HZbr =N'YobI. (^ ׾{_ ?OJ`S`3BN[}5w6:ǵ/iSlt=4F*d&T4y/#. ɵim5Uֲf 眕6Y7 fơ=3dϕq뚩$qTM-%r!$@A? ޾V0c~{[{;򥧅a~ڵ»&ڄv1ek=wb MLkNAԬw-x>~/r=e73VeVN)K%Sښe"+3uXuچrn ֺVzscJ峻m}vb㶓n\YbIUBT%*,0nov=;z꣓S/nSXSpl##k9mXGrZv^Gde!ŷRԠzQyjC]`gToPov{j~KRBMY}i[߶9KL2ԉO0K#m>wB[ٍ+n[[b٦DX ݲpo] [\m5qdT()mo4Oy9Ie b][wղmM~vmi۱~t \}$яimRk(L c Cvk7r9_r1 ;zv|F@KyZ[&jEji/"6$69ml#e]9s\{ScL}Ȣؿ0q/nZ*t,CLoD߉Njǚy=Pgmu6^]l-["çUʖMlʍp-"qmU>۷uFOJ%Ǔkx 'g=睋k[3u,{³WɘݪF]ՍeFX"Oy\,cچ=w/gn Ļ]#2? vqy-gXnR.^}ݺFs{ŝG]}e|#0mjx"ƬWكm?rgU^xVB":Dt>@LRbun~ݭ,w+v⪕;\U(RYa61>#Jm˞Μ9g9XKaG='u8gf}'qy#ɉw J]We.ʲ-<+&q%s?2dњztҼn`cΤmmqMdz O[-ߩӲ&;[tmܝVnr">{x<8U+p:Ig]zjGkt,uzf}dؠoJaکqEq -(:d<պ=eKy[˗^%ZXkX[C2߱\ITTLGzANM￵i]K>UsOGDDD.ZF6* ҃V Zhz{'xp^`wo8r0h ZmJ5"jb[l=yUu7-;7IT%:jFjߖm0tzU'K)څNۧYJ)4IQ}^KWm7kSP>q;ނ#)'n7&׊r?óM{IwR\j2Qn[v pe#/tAF\ϵ225q֒om6z})6҅*oqDsMf CNIN=T S2t,_ѧ}kveMF0J\Rnnݙܹy[rUc-j{yGtkQ%s]5qB.Nw.JN1LvR Ui5J ZESQԙr):MJ+g}χ!2;q([jAud][ljVK3$ײSJI=/|&tl'*n۽f.frܥ jQO8>&Z];.|7T/C}$ڋUmP2Reҭ8hFF\L 3~e v\۫]ݝNmrnB%*]Z«hKc=BTLG :V74$=Ǘy+EX'4tn(I:Ѝ;Df8c,k1%dJ6.j6ź{N~l6&*fœI7 WAlGOu-ҢH,,(ǔe뿋쩨kM܍ZſgRvQ' 9)?n|er˭|I|-fGK.rΛp8XV1%K6mvG+tc+qE&ǸC_Nm:l=_/m5^[dߌڇ.c<%:)tQ$Ow~-aY;UJ>=F)2[nk؆?훐M=l6[4(O.]2#-H^n#->&mp5~Fӛ+|| S,xag%qkEUzUgæBhߕP(7]kFnq?֖CpruZ6*rEڊtS|*tI*E}7R<,nUU֫^I7Q*mSly%rdȓd8hE<9oHhMfNSRj[i7D[Rj݊+kდq{"$$H?p\̅S?㭻;t~R߁)^/>Qj`yt[w ԛ;²~+ߔ_ YW~|o]?x^ᯛ `ʼn;g)T@vWn]>&4lp+$D̢1l|ȨF%-}.9[}w~ ԠLM9hСablfe&QoW!s?wjLK?s7yO>(=C~_nyǜu?v3vyo oI@qV-jeES^[9WoSܝh"l2C1a͔CiJ@3:Pճw=/7ovuk+\V;lDgն<[A+rX~d;m!_s8ݖ׷;;.0llUC+?i#_crʙ1~C.\–q ul8Hܶ2m`ܻM3Tov|Bs rɵ"oLS- DКw=Tv@f'6|YlD͓Y%׵-#Ѯo%:&!3o%\J<02;K87>^vgƓ# ;ݝmz^Y6=PS39U%~ &f# }o!muH;ʲŇ˷yvP+&.7e[3'vR4Yj̗IZ`e˽3o[WU{ m[sUbۋZǾۆl6~9'V*.\S2<Sd*zY[aŶ`]C$n.v^Ʌ dng>ەZ,Mmϑ :n6nϦezWqUJ4! ۇ4R! =>>Fn|Q[{pRO17ƕ~._I''00k=b՛o}Osðc2'o\3}ݭQ^2 . R1yKȣtAݿ-uܾw!`?1Whn|gzUo[ECWwjUIן)^h#1ɭ!/Z np;o;ΗŻkXs."6E`Z1 עӐ9Kl8qd q} 2Stt;#j>;խabONŗ=fwP1j)l6J̶|gV2`y/0E˛6+ԫ1? 6}KW c\KoKͨ2ۅFw–s*TԞLיuDx .kCzWXhy۶gLu|%TnupǺl-S* PRaLnT+c+*xl.v!.U=|; !_L̎뱚U=4hm:ٯ"y)$:>%(n}X'p[ȴ ^˒4kƓmzDx \ 'NqamP7nyN݅=j7%McSڵj%STy qXymvCg{w/w=wSW5r̹u erծˊsOm=DhEҚRb#n)QOxtվQwe]I}wCa'"[ۂ-z}2UuKP$㜉ԧ:mc<Ý>RoL?wu|%ҷ&K y_!y9 ??:tq3(UU-lkS'ɸ@jdzQˬR] EVPW1DJq2n:,c|ǻ̑;y{X,ۂ.u.b˕u.tKBjQ"[S園S`ٮdNبeJ&9Ơ ~0a(Vm٘L+Jr*vڑE( x0+tp˕ n';wm-ޜMOxX>{#2%jgb2M[`K*\5@8l'e=0u+w ֘鳾{y܀:R*Ya]"Ӧ%ktynlۣ65,3gU}{GYrb;ge'TKwǘ.,rpܚV]Tr,!dp /ԺU,xՉ>s׽~W5oTh yx?xrrx?)?ilbT׬,z$Ԏ.UH٠\U1pU:]JwSrGZq8àd驐,N67QYBӢD㏙W!Q25ϸo9ms-7-%3CihO.J鯽-;MZM8ku-7k9S$8]q2E(}bۏI[DKOK}3KUB^u %Y,u.-&f#]'܆o$x`Yu,dzwM;#oKxn;\[d7}Rb+*Y䛂ZuBӱl{j0O̓}LhK;[aֶaGL{Cb#S.T[>߃F]NK"u^LUʐ_ykW?!GRj29͖qa'0[npcDvV)qz9R)PۨM^aJx W] r>];eN3vxdmĘ(5W2K1䪖weF{mE/QP6\u54x5[hۮ-Nk”i[lUgL]J}5 S:EhiUrgHl!ŒJ$pe=q^b͵Q' ?6|R\,JA ڵ"TDꈭ:ymg`B5t%M] <N_zv2_Ortٵ/i/ReӮ*7[qүqEG* m"[I:6e^p"I$jԴęh!m)]GZkcjS!{e^z}+Cѥ9;R|/ֱeiUԏCNu2Zhcٗg$ݭwvr P8*7/Lk~I'Km1+MW%Bk|oOm>-#qj*|Dbѱkn|n{v#jĮqNpMIUm(7Liz;{ҜݞڝVƚVϬ+sO!OstGvxӉ']uӎ4g_ 1^-8ۦ k!)Ύ5O;YSB#2Zzχ;<.ֵOtge~.(RC#wFZeGZٸ6FFJ4e2ˇpJT$[wgV)q6muDGJ56q\I!̗ y/I~RtJ9kJ]Iy*'FN0s.[l!fw'y(7$œ WƫgyΙdMEU JQJv̋vmrۖ.jWR_M֨djYgSj0^\y'EoECjm$ IƩK>Z28J2TiJ2N#}.s cArl嫶nB.FIJ.)۔\ZiM>/hLĸ=C1s[?YMqp|94- 鮝𦔽/k^#NT(Y LS$6˩}{;5 )B۷W$qpN)qqoot}ZDVә;7TiK|6f3h$dԄ}fqݡ>Nb򗉉+ͶO]>ߡ_VtYf79ڰիF sq~prս|QM)g%l0ocJȨHz V;Bb/kLAcfPJ,ԭ{ƍgpjNR6VSI*$!yV足jᇑ.](EܣqM\qJ2eZT).<9UB/(B0j)mtKEj#׿fDI-=rZړj|'Nڤ]k*i$5qt"ݙPM6E4ke^Z8ۏhz$Q(R Ay2zfRñnpnkbkI:=j &ΝșW?׵d{+ύM'??XqeeĽ.[o=UxFS=ӷdZwenՄ]_X=ĭVa* pKs0ބۍfJ3 gz̚i|wnxtjc¼5${(1fXQ65ȼb̶Zkn>%FQMJXӡ{TZEVNᖣimT/37cNJUPnP҂ZOE~"-Rc4^b- FEͧtf5[)S!OZIښݲ͑;tvܡ+N)AR=hCNn;wL16-:特7M$=Tҕ-.R[HٷnXk sn[ҞD-0WS9p9:-Ϸ-jѬNu{ҹfv)[Ľvwfg(ٷfe+0mYj8Q1\ݧg]Eǎvڿc!4#j5̋C2"}BRriFp7=ô\TZ:\BLfj#I22װ<;صZl j 6:l"6]۸ K'6RTѯ^ئOԓV\?$x7s#r:Oh{ց=MmuHԷd{pN /܅:UE#Yy+(SgQ(Щ)RHzw>^Ѿݻ>mK&^ '$Jۻ&w%F|xfz%˳ L~3N?Cy9 v w/{ƿ kz3x> sXv}vP"@WyC z`'톽Dw%-tt yVY\wmuPYQA0iG-2JP,6/gˢ]u.-n!Zw.N7Q]Df}Q0({a\@=i_X7gFǘ8^⻲}G MZ1)WEfO12G+=-B@z\`||w6ċj߬m}UwRox֢I &c~XGP6Qndpvܻul'V7^FJt^{b^B(L~sѣ6@߿^xqU!ڙ5|Vpvef-uӥ^3  FSDɯKD%0r}FF穛r7 +o"V8tv̖NQU!5uFd"bCr^bJ=֤fM#ʳԷP0O-9xRBm\=`r-:;~3Tl(nXtXi%2Vٛ#vwqƴ`L@"H‹qW.j,JM5B[)WܺUeZFqc'V˷1W7V̾-MHФwn8N;HPSdݷC7&2j.W\τGŎ'Vb]c.x+Rx1%C2T{myg[qU|+m:M:շ8҉yWd)ՋWS%%:iqlʹmGwݹ WnNŤѩ5(9hTٵDdGUi-)vSs2 2{OnT$Xck n:¶(lASLeȔBjμPpTb2~N2~%^k[ܗ[Jzs0ӓHBKq[}JَA-$dFQgjxxFv4r/x*Rm% `4J(&iv7SkԲmSH1YWmx 8n.k']:Z˭_W >ڃXЩ. jTq%Aā[E}amc]D:rmHRiu:uӚӢ\p(5-q%e)(۬ҖȽIf<߽pr&ݫVfY91q2ĭEQgYbTGQ&,yL+N$[q*RVۉQ=FuTܻ>f>f㋳8N6$܌n)9&»iˤsX,݅܍ȩv+sRTpO}d?Wn/Inpȸ%O]StQO|v5\}7Zwb.AIVK^:wb{[uݯcytO߶S<{8KSRׁH̏N7ۚ[xkwYy_'ZӵF+>쌛ZUĦreE9F[24De{}@:ExWs-\ǻ7K-\JNvEk%:s˙#κ].oͳ;լ7wB6nwu:$L; DkI#Wz.:Xp(˅v$Sq,wn\qIN-e<5Oe+vuYTpcojUI_ާP8 O 7&VL8z$_B-H-[uh]T{|8=qVRN-:Ij:7PUtXϷmy鉿:RIM~33ӸS2#׳GdŲ5+/Bx{(WzȨ5Y㞎#|˖+ ط.|e<o/rߔX>7s}VE.OVti׽ .5nNJO"95{#q}Ay9do]R"M6z\tnNS-D!@3N_jicWsy*5uٮRcWv/.,j}=S)j5C^> Ie =gu9ӛqjtz]۪TMoߧI!Ǧ¶m:,"[L!{qAv-o 3{"KʼnrIkfٶj2ƙ؄S`7` k6jzޞ?e5G&6uʷ2%ԒRKE*G\Npom F/V |C0.q_eenƣ<5Oh'67ɪn[SĽ{ڔjǘzs;~׌(ۂ`ܢ1ƣ` _l9Va6%UQWh~P~\F^ZHR@:ۧCJ{ôGeBh;~ۧnU J\O+n2 RҠ)ng}Kh{5+S×ܛ.1ZjG)iRȤIN 4%{oΜ/eO[Nffd ĹK?nnԼMqX'܌nZvq<ķbFnͪaQ`5 s,M_լ?-@_{w{ӺձJ}GF[%v\5[ŒGkOw/ΜM9rjË%2+rd~+󲕛C9U۳r[aJǭm|˒LAʨSCq[XMۺoubfp:t+ΤĻo ][ zt-*67kvS7D·MMCQXm;)܎n_h%]4ܙnRk!]ڵsDUF"`R, &#R_*[z*ZqFXɻ]7|۵w+'pFDەs=r./ᐚm3Hשy yD"jHCr':sA65نѮ^o1V/ f;nFr3VM)e*- s D'H݅fӧ\*޷[k<7u<-]֍Q8R h|p=WlW3s%Q %3l}@U-K6f-NϿu|ڴmWN׮[׸F*mW\%r! C78:޳vBG7ŵ.JթԚ2x)ST!řn~9 W:Wpܢ件{xf8ٳwKE ҰWxVB\qBZ 2wMb[lGSnyԚ~z9ZmያvoN2Afnݽjf>)j3 !;gOYʹK" Wftڎ+׭b*2ϻK>ۢӱeyԪXISUm[z+ugX%0lϏnvg!;t{BqPj>PyvR7Cj]O%+ݲ :qiMj6W}3vC/R=4Som]ŗ=ю, TF6U_-\6MyskwMr&Q\wjKܩyMϣUj0*}RZܷSdY3>Zjqj6TgzpA/M`/Cmл,޻feE[/+uk^Vs1W$G(JsW2ٰu*߻q*Y޵.Wi:ur5T),=0uRmho.twܖiYwrWHntvEj8qhf`Ͻpf(R&>Ki%I7$QӖm-2 ~yߗQ-앑/ x[k8nw.c㩵k}]FkbJl:{.(˩n0Hqvαp7 귎.Gupx[N`Yq'+ruU7[ү+>!xrȫoSo]OC# d^Q]\>!ƛGw^Mx"-+%vdX-:M2UR%d>%l ioSu6lsj7D P>XxHz Ukà(n^Q V>5cVtWj SEiJdznyej[lE' 3kuٌNn4JW)gB {4 j6&]' m-(ZMEz8cz>WZ6#7+[,MR-Z!4ܓtCyE|umj1ƽvƷV\;%>Q :#Le(iVz5 4ũۤUWxX ^(ҔsլB2w-V ^R+; ˂M\z+Uwr+RWY⺧~ Q*JcYSNSλUd8in=v K낫k\IRרSUaCFmϿ5̗P|u ZTԕ}>oYѲ1sfP+sQkX8Gb~6r,s>^\,mGL+7[n-E\.Fqḕcl*Jmjb5 ,m]c}NXfeVlǸJ5eˡ$4%g~N p4Y*WwW٧<8v#;qԩTut,m"#Y D\5V`\\Lȋ];LȇiS6ϝZ l>LruR\v=ǘϔDg=ԈdFZ+M{=|,[;0>RiSi4,S5}yxw&(E7&fݙ4UՕ! ~'Id)]ǽu2K-fޭ \08Vڅ쓬=Vy^^ IhyKR-B#Ըr=]mܻӾ'*Umkoy rTqT_i,/8Q^<ݤ|4ԻO(܄"'5N~#m.(Ҿ2i6Uev&I*<}҄$eNtÛzyWJubW^iBW.܅Wڮg]irO6Ve90sgv.+sV޿aޔ[p?3q*FutUo*eL\KM'EG*ZcAFfG5J 5jj=MJ3OK:k˝'NMB7m3uFҕ\-Ywg%PRqMIyZGY9|μvn߻5cWݷa^+X֥vnݘ\v7m>Fgzv"-;Ew֝}1|RjN𿊀7g#֟*GQQ|#/bo]p$>_Un9гUbn9׃ErQBU-^vDmVh'<R[fdHT]*~}3j;nvjc7s-rӳ Y8[n[1pJx kX[Jk9Mn!_Nю6x:iZ˦U |߉^Ԛ݃hYxk &U^bwKk.[jE+P(˞=9j@snCv7%c_7=xǁ<l {t'酚+1F‹l׭:ݻILruǶkL-L(K0L1&>wXB(pm;1fpnlp֓%Skidkt(U +xulo'/ڕeN r=^pZZ:Pnj8Hf"48ijY[ N[yZٻ+=  ø:3 ?^ܷ^Sr#YK[UF?CuhC b]GM')mڏsNrܗI]ljq6VB. W,UK"YX5{c >Iqā> T:n!,5l2VzCl|+I[*SrjnS6٨y+x,@>П.g+!rn9>N|W>OZT_ut Y""v7|sfި;Pclm EùN,{'fNT%U&LfH8~1v>Il}统u6P˗c(WV~H^bMU.o*oOF0N:_:6Smr_.b+|ݶYY غF,mwjv>f*>QM뭱Sd:`N{l/⎱;n-z~"Gze퇎J5S KG9!Gn;N1 ݎ h6m|S?ɂ5'WOÞ 7|7^ao @mxGmi^jϽ>01Mf0լD3-2T. VXR"ɥV Kl J O7|u?bvа;6.eߓ|[1bmRr,eRz`z 6܎-ͨku͹Fː dPhYgZUj}nvX;z=gVեTv_J }\1n7w2J?ޘγc\E 1Aޑzq;\r]]\Y&[nsNei\uURje*Qk2CSl*xJz-xٶlm+|UjUؓ`Ladqiĩ!Gd\W~fz;Tn*PdRM&T4`չSWq5k훶(N"Ӎ% V]֦wb.nUO!u*J&Oӕ2e|Z=eV쫚΅g#+/RW:طnbi*Wyo)p{:ETKؚR(RY+r웓r(IF) VmȵNB:h Q1ғ|u8E]{,'$-TR[j49l*3"I鯴zhd>Q+\BkNF=.$ZR4Nwհ(IpNi.(Gi33#33e$FXK*NdWrud[r{xnk$v2ıh+J1TQ[#JQl[tRO]LHKٮ NӍnF񨔤֞Em'MILB"ԋ%dBŋ+p̿_17jzT~4pc Vo\ƹb9Rq-'1j;8ܗ)hE%DZKS<璸Bu*%*Yw5ڻ9ۣ^z4U; Ñk\U(o~G?VUĎ:?P?_F_Kߤ~ᓾI |pr.Ok\SklRhҪz{­P .}SktZ7UQ4ڌIM8̈eaӊJZ%FFZu,KZvln廐SNFIVtuNi?CM5]+Ph,{jN JSR$IS^tSUVrORYu.9WyP6 [Kiu m!X|]Y79ӄ)\ģ)pbڳr%*&ꑶ_-H*dzk)1 V3')UAϹٶWRxe'պn۫h7AR9 EAJeGLms!%D| A 5]/Q3eb̄vnVn%za\m kZnv([emqrIҕij|""><hjJשvvǕ|Pޟs}V~2&Z?+2N&Z4w@)4iSڪ_>/JN9Hiۏuf8'It[ȲR.hZ$ȋ_Y ~U<UUO*6b)Ovzڜj\R̋.$FsQuҊj^נ䈈y<zZIuP[}Qm=C?zN(Exqu/kn S-FzKZzOסӽjJ\)F3b!r5ٝ|;6 o=-3*λ]αb\abqRi-w޵⦪~b8Kpo)Z=>)ғ"5/GTZLE-輵f7ݘ۹~+&+w/7GFI:l33fg.N~۲\2|*cnermnnM+Fq"ѪIz%j =YW8@~gc/~?N'?)«qȸs➟n=k" X“m֮VreMh2[uݖ] *FܖN)MȐ`f0 g,C9̑o;ddudJ=In13:ݒvvdMUEJLp^,6t-@͐9'{7m{-3,>hnF;ѰM)->>+Ěz!R* :`e--m7nB\u{b U>[8֪]6^ߤLʦ\DFNo$$dͶlgno8OrsQ\l̯hRo8tuNo+ CTxu!2[>ctFpeޓƻֶR"3QrQuOѳgwQr;S~)6HhZw/GgVTmUf_yt7%$];zLWF̰xy2Ʉu!MCmš_0[W6jf#a-KLi+3Q7c^qg%s<1aYIQeZf+}>;S6L0]Yu_h9߻<ƅpmiM$AVvŚ,*#t2.8Y)-Zhshü97/#Oro"u^/uFgWɺ,p:6a,^x%$Yve^3PƗMnTP&yS}OJ '덫MH^:rXԴJۋ/rI;S*,+yz1hv)Qw^ڍJ2oL׊q(\fDj:^T%vOadɂnS}ZO)N*λdaȜkG_PIEO}нa(^iQX᯦-7^)%g'SJx(.S9zVɴZ{E ))ۅi/s7 VIV-|sj0*UBTHIqRf>FP$KqN0 R̻8j\GcC}IUz\i 6F)Q{Gҧ3qSzKj-Az VЛS-zy:8*mNk|D鿓ND2u+0Yŝ7kqm·?8Ib]u>˗^_>(]vӋzv+ݩ){vZrJ2RQ몋C$z [,pp,8mڊbR]Il .f~d/ݓs㓓mͶ{mgjQwn=Oic9ܚm4Q/6ݨ[TƧ?nԶoytf{@AzT{e{[O'ZRZt~AGD?s3􌿂ՉIw'|~U\ w~di:Kޱ)U/sU%njѩ&GSP^ǝd)..!^U` 1wX[aԇSxoFV6_扐)T 2Mfd=ۖͭiZ7KK Bi9%7@<3<ճԻU,},a}FRqɛr i@ONJvK KLN M, ʖv0n-]DwlI-X6ܶ$Jʴh5O+mOI+Ra瞠\ MG7BفjYo1#͖0V`Ѱ2M?c8>-Crt*JkIGS:e#hPKx[鱼>{5m;wcն&>j-M֥^َ) 6yȜl_w{-ō̱r> U=]iw3)r*]:K]6BdCTZ|>gf}LW}[$'Y5 &c -j.z6R 67MԷFMnÌwI7w5E}o޽+K ֵy4܌ȥW"COyR[q5Ӱ͙f[v"_#q{MV6܍3"u9BK(41ӯqˇc${ߝCi6I(OmθzҜ5k^:>Jzw.>qV8{vU[ڶEm|DžBz].KHjI]x;Mɗ{m,qZXr忇2u^RO2Z}ZێS[2Jen!*NDcrBUً4<ǼMҲs1Zw57c3&ĖڻzmP*FuJG1-dN:|OU}ҵgi2t~F^^Z.VxjvŧnNNh<:]^~NN+ge^g.SԔGFe߯'[vn'(ScJ]kܗ7eJOlRrfziݮq̋S"\*U<*W]k$FջV}? 7g#֟*GQQ|#/bo]p$>_Un9;l S VvQU%OLU{οmU6bZ1MTx%!֙Q7, J=!3 ;Q,ڌ;6ͱ݅q^&ߔ·n #WbwӖX.HtG)N&d̵zpI,n cu ޖUj+VXUp[w]N o.J6Z8Ts&utxln;~HPHS/xw`G\ʡ¿rj Z^vt"[L:SD\h0sUwR,}[x^X,R2Vn< ]2YDr[SRKs8tXb̷G?Ps Tv 3be,zVz D[/I.KOEQrm'$7|[J>r S`5յwT#\w1FTz\Ԛ &"ׅhSHrD\'r]~/>p;:Piuu:"9ő=tTaS7V2rӷk7mb[^WmPp*[y.Þ6f]cizJCgRR@UVl큝.WJP1N{/\whZ ػϧӱE7|E֫Sί.x-Y&pi%v''-x6r'Ws*6=DwwUu]=C?MK [yrtܒG$!WGqJ*%SAz ED[^)/tė/g=#Omd.|^n/sl׉g DZqemqowݮRzUܜ=ڽ-o/Iۖ;qVʘgPp|mm;6zGl9.8pwWgsJ2qPbe}}UpNjٯ}7TMQKrؽtEx%v w߾8%|j;~|}pK]ơ/ w߾8%|j;~|}pK]ơ/ w&~e_H 8PL7:%ʭ5Kw&U2vwR_+rm'}C7#rWoO&HoG?M$UR7{FU]u ;# !Wk`|W>׹潇9Vn)6)*ҹ{%qV4q>W1vi#T"Qk&GwxcJBJ- Ϸ^ˁxkU}ԣ/3.;]J=<*)cS)ROK9H=,r zX @)cS)Da^ԽQ gxJI=w֣gf*TRj

#E-mail: gylee@kumoh.ac.kr, TEL: +82-54-478-7293
• Received: April 14, 2023   • Revised: May 23, 2023   • Accepted: June 5, 2023

Copyright © The Korean Society for Precision Engineering

This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

  • 420 Views
  • 3 Download
  • 1 Crossref
  • 1 Scopus
prev next

Full Article

Download PDF Download PDF
  • The objective of this study was to present a rotary manipulating system driven by a rotary actuator based on twisted shape memory alloy (SMA) wires. The rotary actuator was composed of two oppositely twisted SMA wires connecting a rotor and a stator through a shaft. Two oppositely twisted SMA wires could generate bidirectional rotary motions upon actuation of each twisted SMA wire corresponding to the direction against the twist direction of each SMA wire. A manipulator was designed and fabricated by integrating manipulating arms, the rotary actuator, and a Hall effect magnetic rotary encoder which could measure the angular position of the rotary motion. We modeled and characterized the manipulator upon application of a ramp current input to each twisted SMA wire. A proportional-integral-derivative (PID) controller was designed and implemented to control the proposed rotary manipulator. Reference angular position tracking performances of the manipulator were evaluated with a series of experiments.
  • KEYWORDS: Shape memory alloy, Rotary actuator, Manipulator, PID control
  • KEYWORDS: 형상기억합금, 회전 구동기, 매니퓰레이터, PID 제어
For decades, shape memory alloy (SMA) has gathered intense research interests for many scientific and engineering applications, for examples, composites [1-3]; robotics [4-7]; biomimetics [5,8]; biomedical [9]; and wearable devices [10,11]. SMA exhibits large deformation with relatively high power density and can be easily integrated into the structures as many available forms (wire, sheet, etc.) [4,6,12-14]. At low temperature, SMA is represented by the twinned Martensite without external stresses or loads [13,14]. And it is deformable to the detwinned Martensite by external loads at low temperature [13,14]. The deformed (detwinned) SMA is restored to its original shape by applying heat, and it is called the shape memory effect (SME) [13,14].
The property enables SMA applicable for the actuators. In many practical applications, actuation mechanism based on the axial contraction of the SMA wire has been preferred [1,3,4,6,15]. Recently, we proposed a new actuation mechanism for a rotary actuator based on the twisted SMA wires [16], reporting the design and fabrication processes with actuation performances of the rotary actuator.
In the present work, we designed and fabricated a rotary manipulating system driven by a rotary actuator based on the twisted SMA wires. The rotary actuator is composed of two oppositely twisted SMA wires connecting rotor and stator through a shaft. The two oppositely twisted SMA wires generate bidirectional rotary motions upon actuation of each twisted SMA wire corresponding to the direction against the twist direction of each SMA wire. A simple manipulating system was designed and fabricated by integrating the manipulating arms, the rotary actuator, and a Hall effect magnetic rotary encoder which measures the angular position of the rotary motion. We modeled and characterized the transfer function of the manipulating system upon the application of ramp current input to each twisted SMA wire. A proportional-integral-derivative (PID) controller was designed and implemented for the proposed rotary manipulating system. The reference angular position tracking performances of the manipulating system were evaluated with varying the angular velocity and the maximum angular position of the reference ramp inputs.
2.1 Design and Fabrication of the Rotary Actuator using Twisted SMA Wires
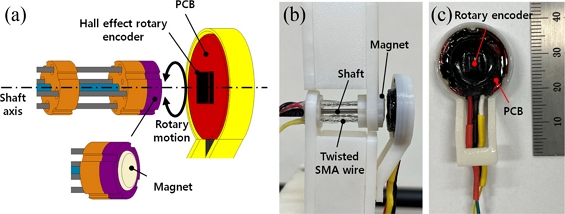
In our earlier report, we proposed a rotary actuator prepared by the twisted SMA wires, with presenting its actuation mechanism; design; fabrication processes; and actuation performances [16]. For the present work, we further developed the technique for a rotary manipulator driven by the similar rotary actuator integrated with the sensor and controller. Fig. 1(a) shows the rotary actuator unit designed and used for the present work. The two oppositely twisted SMA wires (200 μm diameter Flexinol® SMA wire with 70oC of phase transition temperature, Dynalloy, Inc.), denoted by twisted SMA wire 1 and 2, respectively, are folded and adhered through the holes in the rotor and the stator. A UV curable resin (JJOMA UV Resin, Jjomanhan – Maeul) was used for the adhesion. We attached a magnet assembly on top of the rotor so that it generates a magnetic field on the rotary encoder, which senses the angular position of the rotary actuator. A shaft connects the rotor and the stator through their center. The fabricated rotary actuator units are presented in Fig. 1(b). Fig. 1(c) shows the actuator units with the magnet assembly attached.
Fig. 1

(a) A 3D model of the designed rotary actuator. (b) Photo of the fabricated rotary actuator. (c) The rotary actuator with the magnet assembly. (d) The oppositely twisted SMA wires. (e) The twisted SMA wires applied with the UV curable resin and the electrical leads. (f) Photo of the rotor and shaft. (g) Photo of the magnet assembly

KSPE_2023_v40n8_665_f001.jpg
We provide an optical image of the two oppositely twisted SMA wires in Fig. 1(d). Those twisted SMA wires were fabricated by using the same setup and procedures reported in our earlier report [16]. A stepping motor was used to twist the SMA wires (approximately 80 mm long), and the rotating direction of the stepping motor controls the twist direction. The twisted SMA wire generates rotary motion against the twist direction [16]. For the present work, we used the revolutions of the stepping motor as 50, which results in approximately 2 mm of helix pitch within the twisted SMA wires. A UV curable resin is applied surrounding the twisted SMA wires for insulating them during the actuation as shown in Fig. 1(e). Figs. 1(f)-1(g) present optical images of the 3D printed (ABS) rotor/stator, and the magnet assembly, respectively.
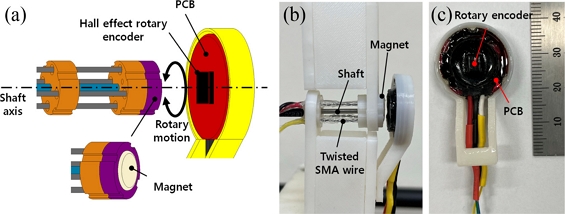
Fig. 2(a) presents a schematic of angular position measurement for the rotary actuator with a Hall effect magnetic rotary encoder. Upon the application of electric current to one of the twisted SMA wire, it generates rotary motion of the rotor about the shaft axis (against the twist direction). The magnet assembly rotates in the same direction. The rotary encoder detects the change of the magnetic field and measures the angular position of the rotor. Fig. 2(b) presents the rotary actuator assembled with the rotary encoder and Fig. 2(c) shows detailed view of the rotary encoder. We modified a commercially available rotary encoder (SME360CAP, SERA) for the present work.
Fig. 2

(a) A schematical illustration of the rotary actuator with the rotary encoder. (b) Photo of the rotary actuator with the rotary encoder. (c) Detailed view of the rotary encoder

KSPE_2023_v40n8_665_f002.jpg
2.2 Design and Fabrication of the Rotary Manipulator
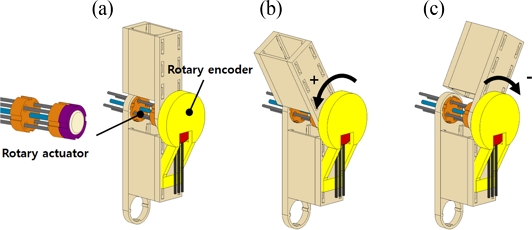
As presented in Figs. 3(a)-3(c), we designed a simple manipulating system composed of two rigid arms (fabricated by a 3D printer using ABS) assembled with the rotary actuator and the rotary encoder. Figs. 3(a)-3(c) schematically show how the upper manipulating arm rotates by the rotary motion of the rotary actuator. We used the sign convention for the rotary motions of the manipulating system as depicted in Figs. 3(b)-3(c).
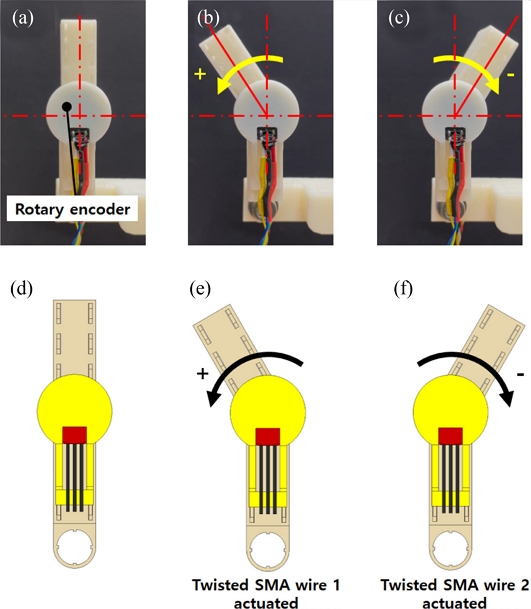
Fig. 3

A schematical illustration of the rotary manipulator with its rotational motions

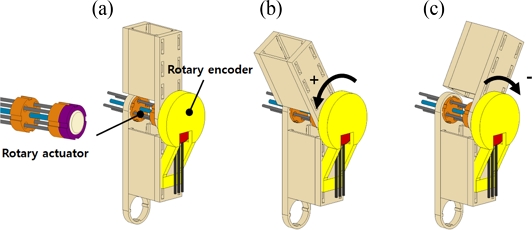
KSPE_2023_v40n8_665_f003.jpg
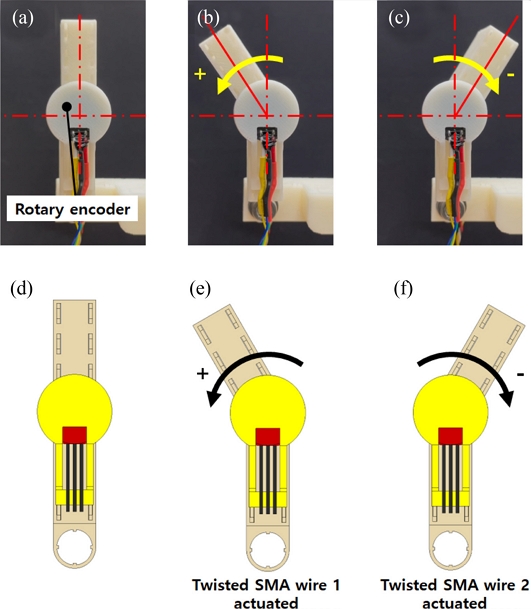
The rotary actuator rotates the manipulator bidirectionally by application of electrical current to each twisted SMA wire. The rotary encoder integrated into the manipulator measures the angular position of the rotor. Figs. 4(a)-4(c) capture the resulting rotary motions of the manipulating system upon sequential application of electrical current (1.5 A) to each twisted SMA wire (denoted by twisted SMA wire 1 and 2, respectively) with schematic representations in Figs. 4(d)-4(f).
Fig. 4

(a)-(c) The fabricated rotary manipulator and the resulting rotary motions generated by the applied electric current to the twisted SMA wires in the rotary actuator. (d)-(f) Schematic illustrations of the rotary motions of the manipulator

KSPE_2023_v40n8_665_f004.jpg
An experimental setup composed of the rotary manipulator, a custom-made current driver, and a DAQ board (NI-USB6211) was built and used for the experiments; Fig. 5 presents the experimental setup. We built and used a custom software to drive and control the rotary manipulator by using LabView.
Fig. 5

Experimental setup composed of the manipulator, current driver, and DAQ system

KSPE_2023_v40n8_665_f005.jpg
4.1 Characterization of the Rotary Manipulator
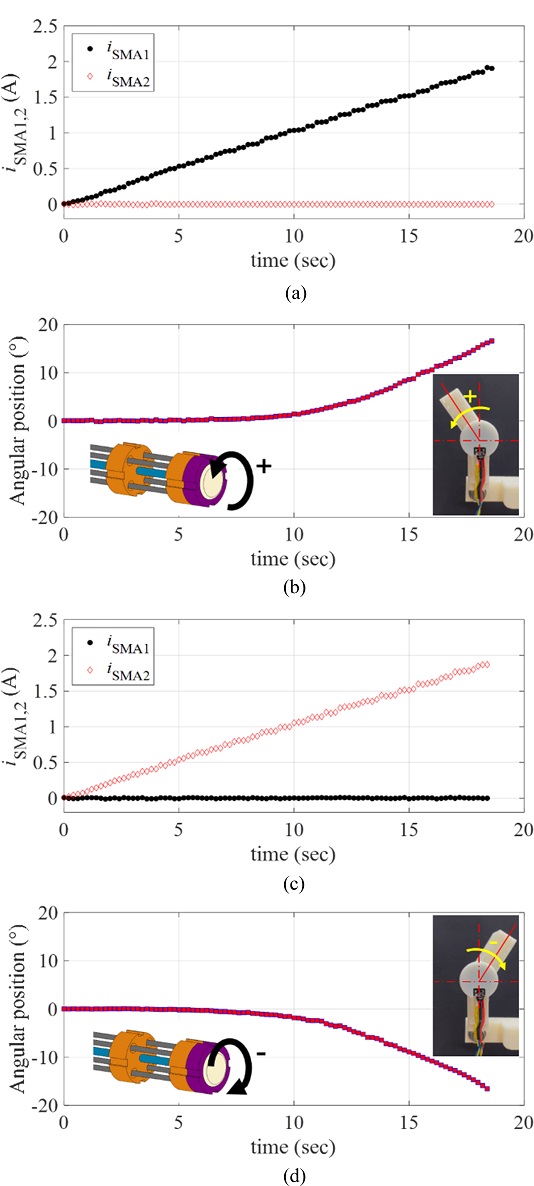
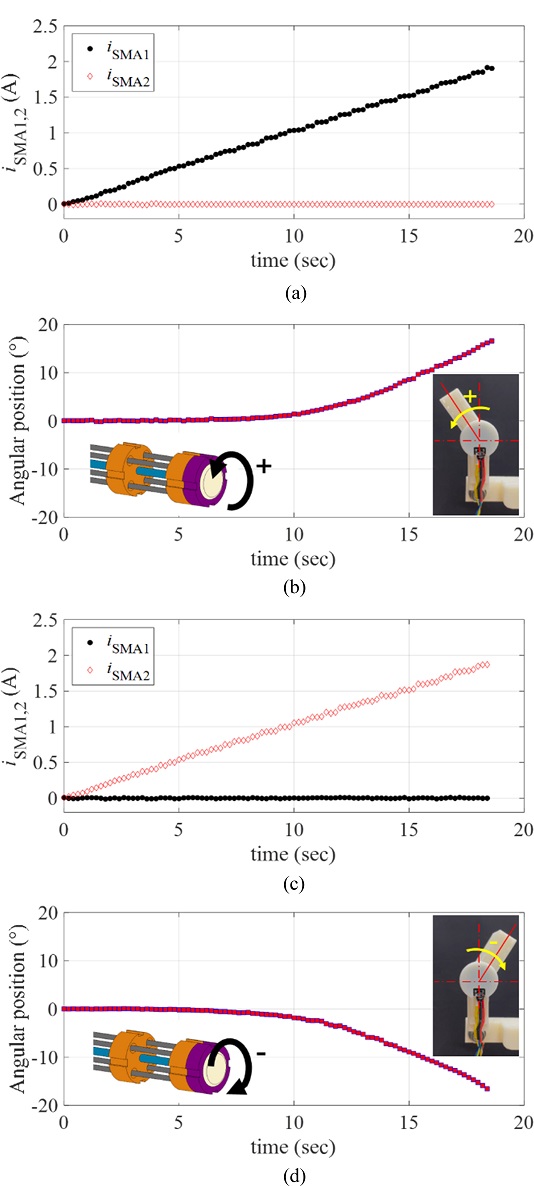
To characterize the response of the manipulator driven by the proposed rotary actuator, we applied a ramp current input to each twisted SMA wire (denoted by iSMA1 and iSMA2, respectively). We defined the positive rotating direction of the actuator as the rotating direction corresponds to the twisted SMA wire 1; denoted by SMA1. For the positive rotary motion, we applied the ramp current input to the SMA1 as iSMA1(t) = 0.1t A for 18 sec, while the current to the SMA2 was zero.
Fig. 6(a) plots the applied currents (iSMA1 and iSMA2) to the twisted SMA wires. Fig. 6(b) provides the resulting angular position of the manipulating arm in the positive direction, measured by the rotary encoder. For the negative rotary motion, we applied the same ramp current input to the SMA2 as iSMA2(t) = 0.1t A for 18 sec, while the current to the SMA1 was zero as shown in Fig. 6(c). Fig. 6(d) captures the resulting angular position of the manipulating arm in the negative direction, measured by the rotary encoder. As shown in Figs. 6(b) and 6(d), there exists the minimum current level from which the angular position starts to be recognizable (approximately 0.5 A and 0.3 A for the positive and negative directions, respectively). In other words, the rotary motions of the SMA wires are not initiated at the input current smaller than those values. It is expected that the temperature-induced phase transformation of the SMA wire is not sufficiently initiated at the electrical current smaller than those values.
Fig. 6

(a), (c) The current input to the twisted SMA wires, and (b), = [ + ] (d) the resulting angular position of the manipulator; (b) motion in the positive direction, (c) motion in the negative direction

KSPE_2023_v40n8_665_f006.jpg
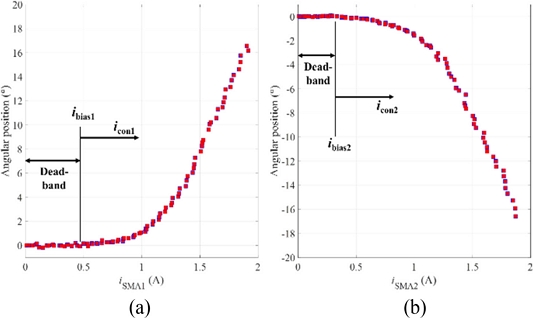
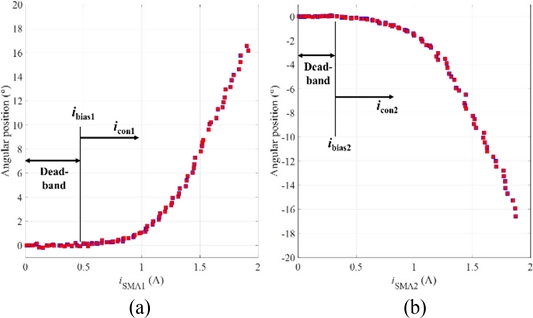
We also plotted the measured angular position of the rotary actuator with respect to the amplitude of the input current in Figs. 7(a)-7(b). As the input current had values from zero to specific values (approximately, 0.45 A and 0.3 A for the positive and negative rotating directions, respectively), the rotary actuator showed nearly zero angular motions. The rotary actuator started to rotate the manipulating arm at the input currents larger than those values. We define the dead-band of the rotary actuator at which it does not respond (or its response is negligible) to the input current. The upper bounds of the dead-band are defined as the bias currents (denoted by ibias1 and ibias2 for the SMA1 and SMA2, respectively). And the control inputs to each twisted SMA wire (denoted by icon1 and icon2 for the SMA1 and SMA2, respectively in Fig. 7) are used to model the system response upon the ramp input was applied.
Fig. 7

Angular position of the rotary actuator with respect to the amplitude of the input current (a) in the positive, (b) in the negative directions

KSPE_2023_v40n8_665_f007.jpg
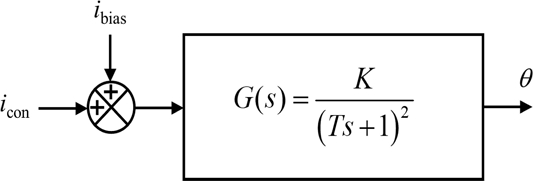
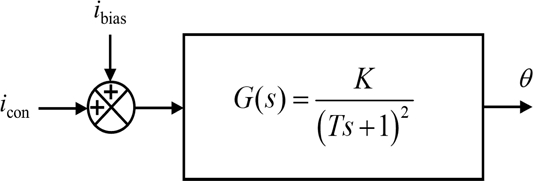
The resulting block diagram of the rotary manipulating system is presented in Fig. 8. We modeled the rotary manipulator as a critically damped second order system with the gain K and the time constant T. The response of the system upon the application of the ramp input icon(t) = 0.1t is obtained as in Equation (1) [17].
(1)
θt=0.1Kt-2T+t+2Te-t/T
Fig. 8

Block diagram representation of the rotary manipulating system

KSPE_2023_v40n8_665_f008.jpg
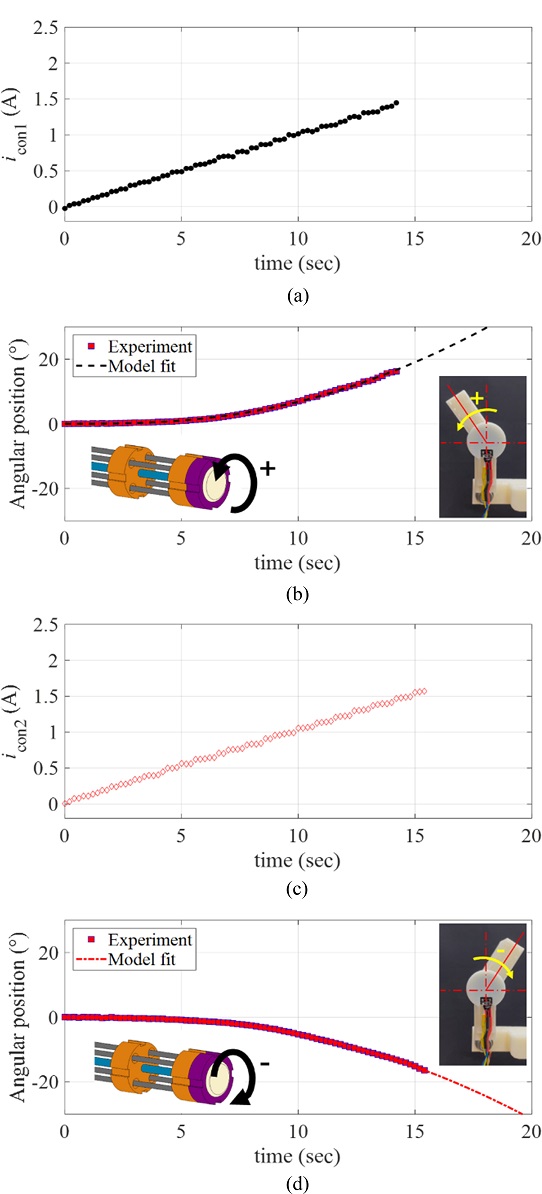
We plotted the ramp responses of the rotary actuator in the positive and negative directions in terms of the control inputs icon1 and icon2 in Fig. 9, where icon1(t) = icon2(t) = 0.1t A. The model fitted responses following Equation (1) are plotted together in Figs. 9(b) and 9(d) with the experimental data. Table 1 summarizes the fitting coefficients K and T of the model obtained by nonlinear least square curve fits, with the coefficient of determination R2.
Fig. 9

(a), (c) The ramp inputs to the rotary manipulator icon1 and icon2, and (b), (d) the ramp responses of the rotary actuator in the (b) positive and (d) negative directions with the model fits

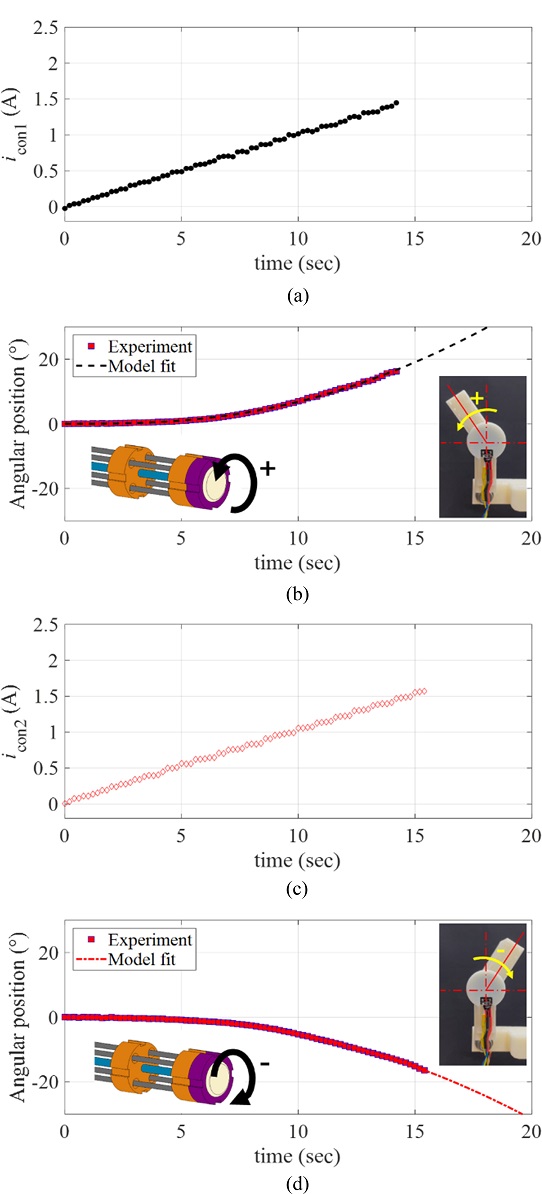
KSPE_2023_v40n8_665_f009.jpg
Table 1

The system parameters obtained from the model fits of the ramp responses

Table 1
Positive direction Negative direction
K 83.4797 105.3464
T 11.5931 15.6548
R 2 0.9986 0.9989
The system parameters (K and T) obtained from the ramp responses showed small variations between the positive and negative directions. We expect those variations are mainly caused by the quality variations in the manufacturing processes of each twisted SMA wire, and the manipulator assembly.
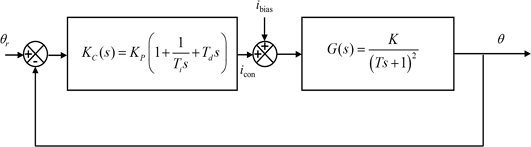
4.2 Controller Design and Performance Evaluations
We implemented a PID controller to the rotary manipulator and evaluated the reference angular position tracking performances. The block diagram of the feedback control system with the PID controller is shown in Fig. 10.
Fig. 10

Block diagram representation of the feedback control system

KSPE_2023_v40n8_665_f010.jpg
We first designed a PI controller with the controller gain KP and the integral time Ti based on the Ziegler-Nichols tuning rules [17]. And a small derivative action with the derivative time Td was added to the controller. For the gain tuning, the average values of the system parameters (K and T) in the positive and negative directions obtained from the ramp responses were used. The resulting controller gain KP, integral time Ti, and derivative time Td are summarized in Table 2.
Table 2

The gain, integral time, and derivative time of the PID controller

Table 2
Controller parameter Value
K P 0.90
Ti [sec] 45.41
Td [sec] 0.60
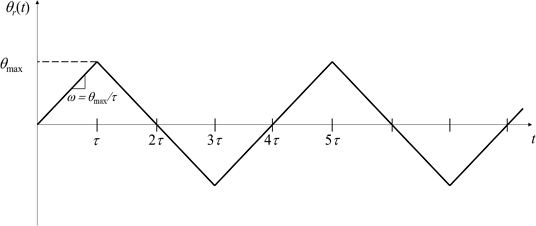
To evaluate the performance of the control system, we considered the ramp reference angular position θr(t) as shown in Fig. 11. The slope of the ramp reference input is defined by the angular velocity ω = θmax/t, and we varied the angular velocity ω and the maximum angular position θmax for the experiments.
Fig. 11

Schematic representation of the ramp reference angular position

KSPE_2023_v40n8_665_f011.jpg
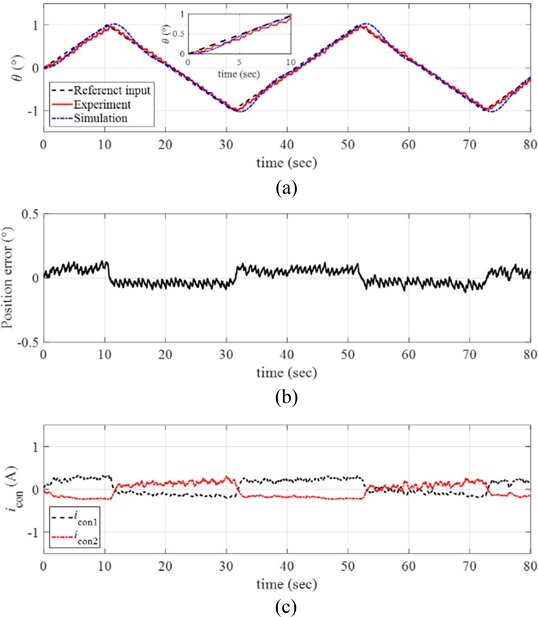
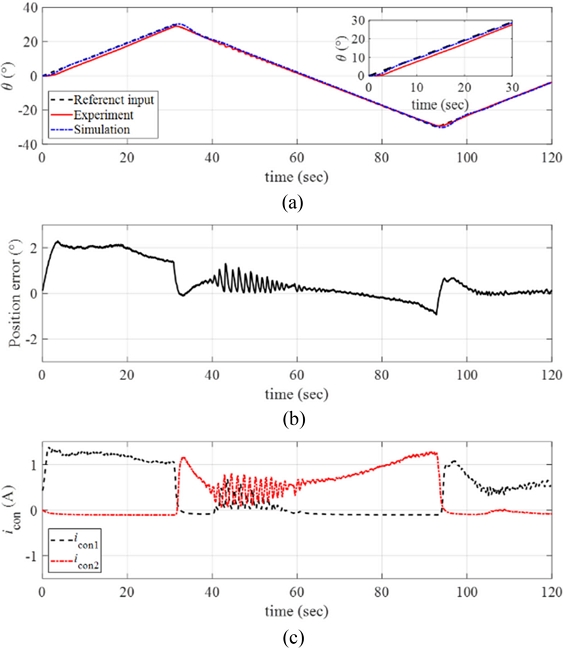
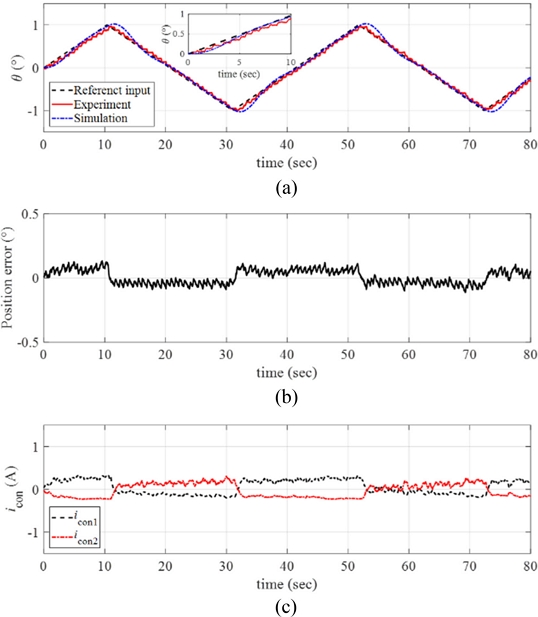
We implemented the designed PID controller with a custom-made control software using LabView and captured the angular position of the manipulator upon the applications of ramp reference inputs. The maximum current input to the twisted SMA wires was limited by 2 A to prevent overheating and failures of the SMA wires. Fig. 12(a) plots the response of the manipulator obtained from the reference angular position tracking experiments by setting the angular velocity and the maximum angular position of the ramp reference input as ω = 0.1o/sec and θmax = 1o, respectively. The inset in Fig. 12(a) shows the magnified image of the data. We conducted numerical simulations of the response using MATLAB and the simulated response is plotted together in Fig. 12(a). The control system follows the reference angular position well with small position error as shown in Fig. 12(b). Fig. 12(c) presents the control input currents to each twisted SMA wire during the experiments.
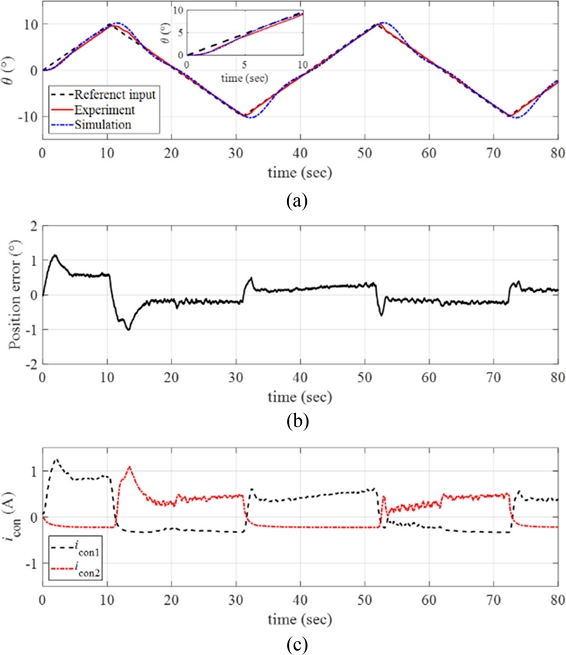
Fig. 12

(a) Response of the manipulator with the reference input and the simulated signals (ω = 0.1o/sec and θmax = 1o). (b) Position error. (c) The control inputs to each twisted SMA wire. Inset in (a) magnified image of the data

KSPE_2023_v40n8_665_f012.jpg
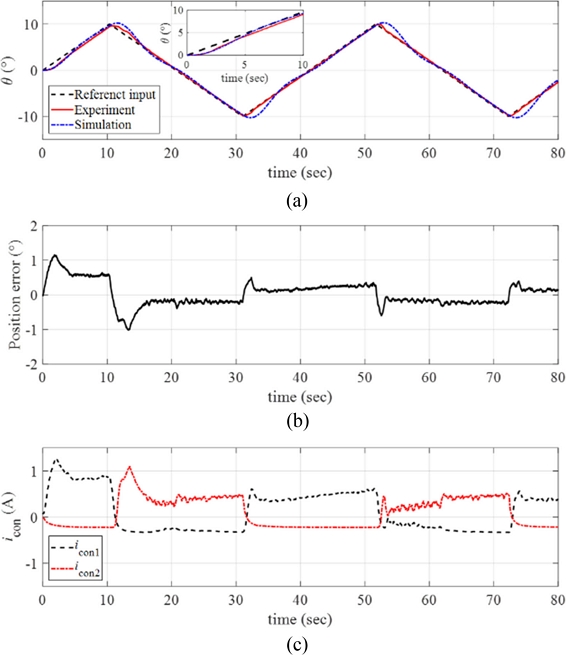
We increased the maximum angular position of the ramp reference input θmax = 10o with the same angular velocity ω = 0.1 o/sec. The results are plotted in Fig. 13(a) along with the simulated signals. As the magnitude of the reference input increased to 10o, the response of the control system still follows the reference input well; see position error presented in Fig. 13(b). Fig. 13(c) plots the control input currents to each twisted SMA wire during the experiments, and we observe the increases in the control inputs for the manipulator to follow larger reference inputs.
Fig. 13

(a) Response of the manipulator with the reference input and the simulated signals (ω = 0.1o/sec and θmax = 10o). (b) Position error. (c) The control inputs to each twisted SMA wire. Inset in (a) magnified image of the data

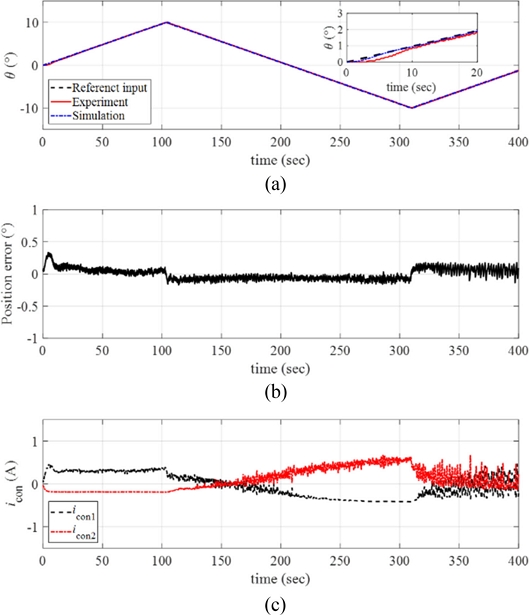
KSPE_2023_v40n8_665_f013.jpg
We conducted experiments with faster angular velocity of the ramp reference input as ω = 1o/sec. Fig. 14(a) captures the angular position of the manipulator with the reference ramp input (where θmax = 10o) and the simulated signals. As presented in Fig. 14(b), the response of the manipulator exhibits relatively larger position error compared to the results with slower angular velocity. Fig. 14(c) plots the control input currents during the experiments. Referring to Fig. 14(c), larger control inputs are required for tracking faster angular velocity of the reference input.
Fig. 14

(a) Response of the manipulator with the reference input and the simulated signals (ω = 1o/sec and θmax = 10o). (b) Position error. (c) The control inputs to each twisted SMA wire. Inset in (a) magnified image of the data

KSPE_2023_v40n8_665_f014.jpg
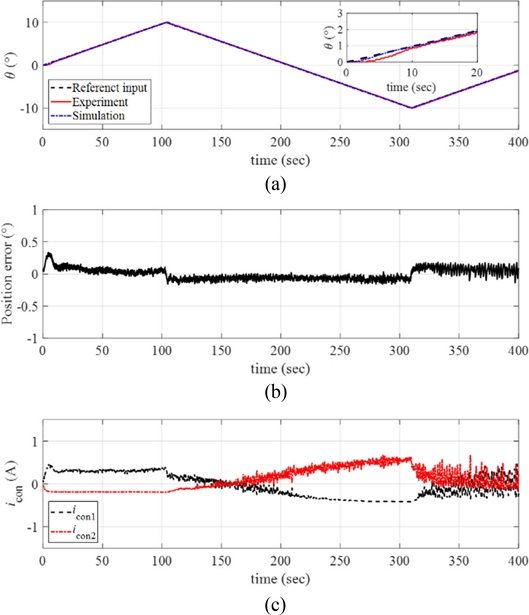
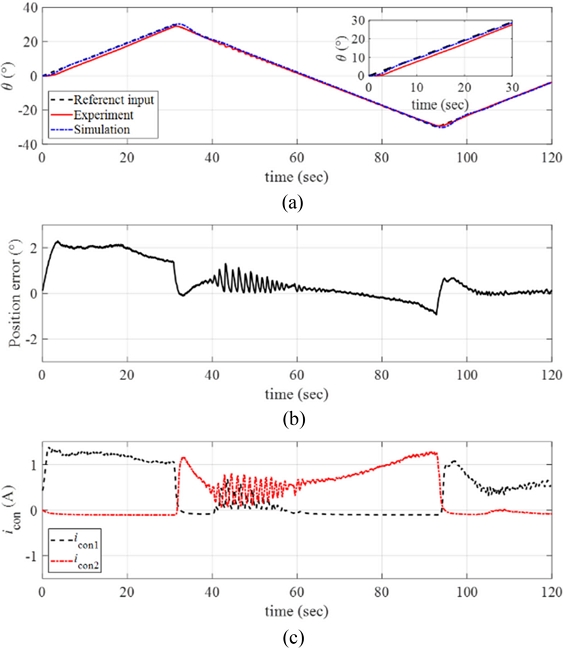
The maximum angular position of the ramp input was further increased to θmax = 30o with the same angular velocity (ω = 1o/sec), and the experimental results are plotted in Fig. 15(a) with the position error in Fig. 15(b) and the control inputs in Fig. 15(c). The manipulator followed the reference position with position error smaller than 2o as shown in Fig. 15(b). The control currents required higher values for tracking larger magnitude of the reference input.
Fig. 15

(a) Response of the manipulator with the reference input and the simulated signals (ω = 1o/sec and θmax = 30o). (b) Position error. (c) The control inputs to each twisted SMA wire. Inset in (a) magnified image of the data

KSPE_2023_v40n8_665_f015.jpg
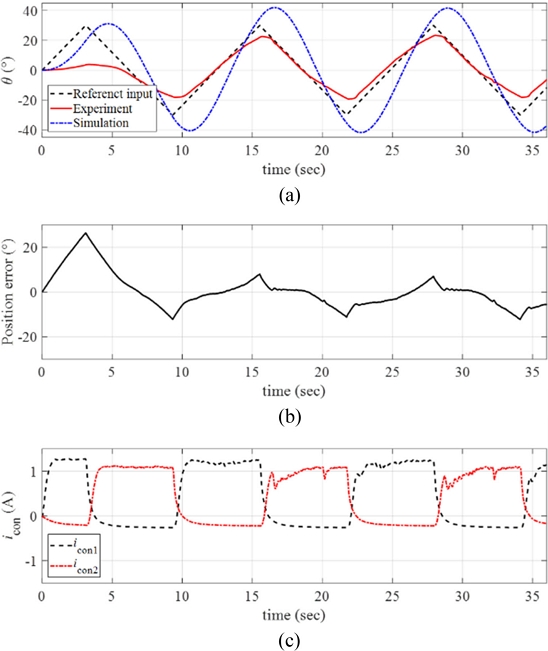
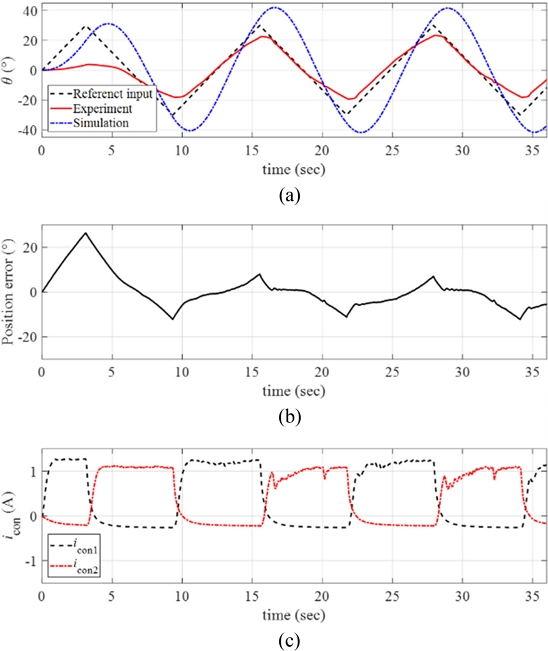
Finally, much faster reference input was considered with the angular velocity ω = 10o/sec. We applied the maximum angular position of the ramp reference input as θmax = 30o. The resulting response of the rotary manipulator is presented in Fig 16(a) with the position error and the control inputs in Figs. 16(b) and 16(c), respectively. Referring to Figs. 16(a)-16(b), the manipulator could not sufficiently follow the faster reference input and large position error was observed during the motions. Since we limited the current input to the SMA wire (iSMA = ibias + icon) as iSMA,max = 2 A, we observed almost saturated control input currents during the motions.
Fig. 16

(a) Response of the manipulator with the reference input and the simulated signals (ω = 10o/sec and θmax = 30o). (b) Position error. (c) The control inputs to each twisted SMA wire

KSPE_2023_v40n8_665_f016.jpg
It is noted that further tunes of the controller gains with considering advanced controllers will improve the reference tracking performance of the system. We remain the related studies for our future works.
In this study, we presented design and fabrication of a rotary manipulator driven by a rotary actuator based on the twisted SMA wires. The dynamic response of the manipulator was characterized by ramp response, and a PID controller was implemented for the position control of the manipulator. The reference angular position tracking performances of the manipulating system were evaluated upon the ramp reference inputs applied with varying the angular velocity and the maximum angular position of the ramp input. The proposed manipulator reliably followed the reference input with position error smaller than 2o up to 30o of the maximum angular position under 1o/s of the angular velocity. While the proposed rotary actuator has benefits for miniaturization; integration into the assembly; with its relatively easy control of the bidirectional motion, it has limited operating range and has difficulties for achieving continuous rotary motion with the present form, when it is compared to conventional electric motors. Further studies for overcoming the limitations with the improvements of the performance by re-designing and improving the manipulator with the controller will be followed as our future works.
This research was supported by the National Research Foundation of Korea (NRF) grant funded by the Korea government (MEST) (No. NRF-2020R1A2C4001731) and Kumoh National Institute of Technology (No. 202001090001).
  • 1.
    Rodrigue, H., Wang, W., Bhandari, B., Han, M.-W., Ahn, S.-H., (2015), SMA-based smart soft composite structure capable of multiple modes of actuation, Composites Part B: Engineering, 82, 152-158.
    10.1016/j.compositesb.2015.08.020
  • 2.
    Ashir, M., Cherif, C., (2020), Development of shape memory alloy-based adaptive fiber-reinforced plastics by means of open reed weaving technology, Journal of Reinforced Plastics and Composites, 39(15-16), 563-571.
    10.1177/0731684420920941
  • 3.
    Han, M.-W., Kim, M.-S., Ahn, S.-H., (2020), Shape memory textile composites with multi-mode actuations for soft morphing skins, Composites Part B: Engineering, 198, 108170.
    10.1016/j.compositesb.2020.108170
  • 4.
    Lee, J.-H., Chung, Y. S., Rodrigue, H., (2019), Long shape memory alloy tendon-based soft robotic actuators and implementation as a soft gripper, Scientific Reports, 9(1), 11251.
    10.1038/s41598-019-47794-1
  • 5.
    Koh, J.-S., Cho, K.-J., (2012), Omega-shaped inchworm-inspired crawling robot with large-index-and-pitch (LIP) SMA spring actuators, IEEE/ASME Transactions On Mechatronics, 18(2), 419-429.
    10.1109/TMECH.2012.2211033
  • 6.
    Song, S.-H., Lee, J.-Y., Rodrigue, H., Choi, I.-S., Kang, Y. J., Ahn, S.-H., (2016), 35 Hz shape memory alloy actuator with bending-twisting mode, Scientific reports, 6(1), 21118.
    10.1038/srep21118
  • 7.
    Li, J., Zu, L., Zhong, G., He, M., Yin, H., Tan, Y., (2017), Stiffness characteristics of soft finger with embedded SMA fibers, Composite Structures, 160, 758-764.
    10.1016/j.compstruct.2016.10.045
  • 8.
    Hwang, J., Wang, W. D., (2022), Shape memory alloy?based soft amphibious robot capable of seal?inspired locomotion, Advanced Materials Technologies, 7(6), 2101153.
    10.1002/admt.202101153
  • 9.
    Zainal, M. A., Sahlan, S., Mohamed Ali, M. S., (2015), Micromachined shape-memory-alloy microactuators and their application in biomedical devices, Micromachines, 6(7), 879-901.
    10.3390/mi6070879
  • 10.
    Jeong, J., Yasir, I. B., Han, J., Park, C. H., Bok, S.-K., Kyung, K.-U., (2019), Design of shape memory alloy-based soft wearable robot for assisting wrist motion, Applied Sciences, 9(19), 4025.
    10.3390/app9194025
  • 11.
    Park, S. J., Park, C. H., (2019), Suit-type wearable robot powered by shape-memory-alloy-based fabric muscle, Scientific Reports, 9(1), 9157.
    10.1038/s41598-019-45722-x
  • 12.
    Nespoli, A., Besseghini, S., Pittaccio, S., Villa, E., Viscuso, S., (2010), The high potential of shape memory alloys in developing miniature mechanical devices: A review on shape memory alloy mini-actuators, Sensors and Actuators A: Physical, 158(1), 149-160.
    10.1016/j.sna.2009.12.020
  • 13.
    Jani, J. M., Leary, M., Subic, A., Gibson, M. A., (2014), A review of shape memory alloy research, applications and opportunities, Materials & Design (1980-2015), 56, 1078-1113.
    10.1016/j.matdes.2013.11.084
  • 14.
    Soother, D. K., Daudpoto, J., Chowdhry, B. S., (2020), Challenges for practical applications of shape memory alloy actuators, Materials Research Express, 7(7), 073001.
    10.1088/2053-1591/aba403
  • 15.
    Akbari, S., Sakhaei, A. H., Panjwani, S., Kowsari, K., Serjouei, A., Ge, Q., (2019), Multimaterial 3D printed soft actuators powered by shape memory alloy wires, Sensors and Actuators A: Physical, 290, 177-189.
    10.1016/j.sna.2019.03.015
  • 16.
    Jang, E.-J., Lee, S.-Y., Kim, K.-H., Lee, G.-Y., (2022), Design and fabrication of a millimeter-scale rotary actuator based on the twisted shape memory alloy (SMA) wires, Journal of the Korean Society for Precision Engineering, 39(6), 403-410.
    10.7736/JKSPE.022.034
  • 17.
    Ogata, K., (2010), Modern control engineering fifth edition, Prentice Hall.
Gil-Yong Lee
KSPE_2023_v40n8_665_bf001.jpg
Associate Professor in the Department of Mechanical Engineering, Kumoh National Institute of Technology. His research interests are integrated manufacturing system, sensors/actuators, composites, vibration, control, and additive manufacturing.
Su-Yeon Lee
KSPE_2023_v40n8_665_bf002.jpg
M.S. candidate in the Department of Mechanical Engineering, Kumoh National Institute of Technology. Her research interests are soft robotics, shape memory alloy, smart materials and structures.

Download Citation

Download a citation file in RIS format that can be imported by all major citation management software, including EndNote, ProCite, RefWorks, and Reference Manager.

Format:

Include:

Design, Fabrication, and Control of a Rotary Manipulator driven by Twisted Shape Memory Alloy (SMA) Wires
J. Korean Soc. Precis. Eng.. 2023;40(8):665-673.   Published online August 1, 2023
DOI: https://doi.org/10.7736/JKSPE.023.039
Download Citation

Download a citation file in RIS format that can be imported by all major citation management software, including EndNote, ProCite, RefWorks, and Reference Manager.
Format:
Include:
Design, Fabrication, and Control of a Rotary Manipulator driven by Twisted Shape Memory Alloy (SMA) Wires
J. Korean Soc. Precis. Eng.. 2023;40(8):665-673.   Published online August 1, 2023
DOI: https://doi.org/10.7736/JKSPE.023.039
Close

Figure

  • 0
  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
Design, Fabrication, and Control of a Rotary Manipulator driven by Twisted Shape Memory Alloy (SMA) Wires
Image Image Image Image Image Image Image Image Image Image Image Image Image Image Image Image
Fig. 1 (a) A 3D model of the designed rotary actuator. (b) Photo of the fabricated rotary actuator. (c) The rotary actuator with the magnet assembly. (d) The oppositely twisted SMA wires. (e) The twisted SMA wires applied with the UV curable resin and the electrical leads. (f) Photo of the rotor and shaft. (g) Photo of the magnet assembly
Fig. 2 (a) A schematical illustration of the rotary actuator with the rotary encoder. (b) Photo of the rotary actuator with the rotary encoder. (c) Detailed view of the rotary encoder
Fig. 3 A schematical illustration of the rotary manipulator with its rotational motions
Fig. 4 (a)-(c) The fabricated rotary manipulator and the resulting rotary motions generated by the applied electric current to the twisted SMA wires in the rotary actuator. (d)-(f) Schematic illustrations of the rotary motions of the manipulator
Fig. 5 Experimental setup composed of the manipulator, current driver, and DAQ system
Fig. 6 (a), (c) The current input to the twisted SMA wires, and (b), = [ + ] (d) the resulting angular position of the manipulator; (b) motion in the positive direction, (c) motion in the negative direction
Fig. 7 Angular position of the rotary actuator with respect to the amplitude of the input current (a) in the positive, (b) in the negative directions
Fig. 8 Block diagram representation of the rotary manipulating system
Fig. 9 (a), (c) The ramp inputs to the rotary manipulator icon1 and icon2, and (b), (d) the ramp responses of the rotary actuator in the (b) positive and (d) negative directions with the model fits
Fig. 10 Block diagram representation of the feedback control system
Fig. 11 Schematic representation of the ramp reference angular position
Fig. 12 (a) Response of the manipulator with the reference input and the simulated signals (ω = 0.1o/sec and θmax = 1o). (b) Position error. (c) The control inputs to each twisted SMA wire. Inset in (a) magnified image of the data
Fig. 13 (a) Response of the manipulator with the reference input and the simulated signals (ω = 0.1o/sec and θmax = 10o). (b) Position error. (c) The control inputs to each twisted SMA wire. Inset in (a) magnified image of the data
Fig. 14 (a) Response of the manipulator with the reference input and the simulated signals (ω = 1o/sec and θmax = 10o). (b) Position error. (c) The control inputs to each twisted SMA wire. Inset in (a) magnified image of the data
Fig. 15 (a) Response of the manipulator with the reference input and the simulated signals (ω = 1o/sec and θmax = 30o). (b) Position error. (c) The control inputs to each twisted SMA wire. Inset in (a) magnified image of the data
Fig. 16 (a) Response of the manipulator with the reference input and the simulated signals (ω = 10o/sec and θmax = 30o). (b) Position error. (c) The control inputs to each twisted SMA wire

Fig. 1

Fig. 2

Fig. 3

Fig. 4

Fig. 5

Fig. 6

Fig. 7

Fig. 8

Fig. 9

Fig. 10

Fig. 11

Fig. 12

Fig. 13

Fig. 14

Fig. 15

Fig. 16

Design, Fabrication, and Control of a Rotary Manipulator driven by Twisted Shape Memory Alloy (SMA) Wires
Positive direction Negative direction
K 83.4797 105.3464
T 11.5931 15.6548
R 2 0.9986 0.9989
Controller parameter Value
K P 0.90
Ti [sec] 45.41
Td [sec] 0.60
Table 1 The system parameters obtained from the model fits of the ramp responses
Table 2 The gain, integral time, and derivative time of the PID controller

Table 1

Table 2

JKSPE : Journal of the Korean Society for Precision Engineering

ABOUT

BROWSE ARTICLES

EDITORIAL POLICIES

FOR CONTRIBUTORS

© Korean Society for Precision Engineering.