Skip to main navigation Skip to main content
  • E-Submission

JKSPE : Journal of the Korean Society for Precision Engineering

OPEN ACCESS
Search
Advanced Search
ABOUT
BROWSE ARTICLES
EDITORIAL POLICIES
FOR CONTRIBUTORS

Articles

Page Path

REGULAR

원형 플렉셔 힌지의 축방향 연성 계산을 위한 새로운 현상-기반 이론식의 유도와 검증

문준희1, 신현표2,#orcid

Derivation and Verification of Novel Phenomenon-based Theoretical Formulas for the Axial Compliance of Circular Flexure Hinges

Jun-Hee Moon1, Hyun-Pyo Shin2,#orcid
Journal of the Korean Society for Precision Engineering 2025;42(1):47-55.
Published online: January 1, 2025

1 유한대학교 기계공학과

2 동양미래대학교 로봇자동화공학부

1 Department of Mechanical Engineering, Yuhan University JFIFddDuckydqhttp://ns.adobe.com/xap/1.0/ Adobed     ! 1AQa"q 2#w8B36v7XRr$9bCt%u&Ws'(xy4T5fH  !1AQaq"2B Rbr#u67Ѳ3sTt5v8Sc$4ĂCÔ%UӅFV ?_Aנj- H>>,m*>fzp"TrKkr^r.|_&]|*vPuܶvoQ1mwVJUhu-I"=LniAƕ8"۲ k*ҿ[yu:.vUQ+)%F DHyVBk>Hy8jݹ q~9D4KRmzQ)^ʔ.J%k_tVi5NTjg!'ky|5asOȻ)R۸ߩFMԿ3L4j6dڜ#NIwUF]JqB/(FafJRzq3\G՛ ?~\ 6)6W4m[O^L0E&rRMض*C .]Unl-1 1r#Rj/&QɈ׉˩s6Rj=5Tg.y.·Pӡ:JJS:C8-2u]d&vUz;7p9 5VnL֢"y)">iי(IDDd| Yj0; LRfS:ktYK%*N2^m|&dğth":ey)uPQZW)gcC3Pv&MMWd&Ŵ۲mvTRoժM03*F3Yd6\8,\hݻ kߔi<k NTwSԪmljj[>->ptU%'LR>&EBH$MQAUx[$Z6vi&_a.KIQ{hyƒ j"JOC9eFҝfj;˚Ω<[3_m% lQ@4g=5$(J]Yc-OMq<Ǎ wSzڗ)k$7VIP붾ͯnV+卵*t]iЎD31~SA1éC2u)ʼnQn-Uoi3:grI8ؓWm*G zܕ)ZקJ}Y YlGeJ6cB2I NS3Q>k=KTBT]W6+SOXQgGR? telˊ%-Re\hѯ2TF"C/OJΩ6r[N.0{SpljjX1“jOsӥ;ҭhe}xu`Ք&.)yO̒ Fߑ.$Qw;9Iw2o+RVJMSOj[SoҌZ%;`d$blQ{Ro{Imڌ>3egf\O֝Uzx"䢸g+mv%Gʆ:|V[N'&ס-ޝ'kfE|K,G&˳98Juin/\\Qݿ̋v~Ǩ!rtWU d|E߫R4d}.qPw*Ӭv5YEcn~f5c%MTMkb-F>5JT,})QHg%{("ӔȸWMsYyWNRrkkJr0XドnͫT}r-jj,Ŕʍ\Q2Ri>v$5!]"JB2WɅ)]VԜUc8i|.jeRO6^V.¸ Q&#|ܶ-*uOG%JAtRZRr]FFG\۩w+?'zչSѧt jz>KW&ot{7P&2D;&\\>Q2JzܗAKSfeNn[jRrԕf6,q,F1tRfԗ>vֶևj-&R'Zi2=xv~Elbsvm8=ӛ"ū񕜈BȩlWau[]ٷBߨF~J!|Ipr3R̴#Yp)={7:G{+:\W}n|Q#%)7^-h"Ƒq:M*%J&$T軨I333׎g_- ucBwwjp[6i25$̏bU’ٱRv?G\~#Iͪb7<<}Ezt" q_Inw,7-d,G÷%T* Wg1"䥱kq/A.,_KhqŒxwvo u2ۥۧ.bQ}XκA$֣ +K״ZUNmڸII{.v{5z5ѮRme[moyƾd~cRݾK'j.\i&/S6f|b=5: p!6i_ 4j6=.si˧eƾtS^c.Y^RJVS-Vi3,esi08?H$GvZgg?gi䤟2adw릿:"۪lkSN>q-4kI܋ێe̊qۅgDoѨ9; #T.Q;7#~_Ufstb_'w~Xw1Xk,vcOt._}v}8"(4Z\ۘgk?J?bm_c!g{HZV]Fkk%~gEt)b秴vΰB|꽸}mp~E6ݹv;7P٤v+ri*3Ԣ|'O14_~7nP{7ZU\Vű[ +7󖱅o#:ǥŬ\|3r%TJX]V7ez¨Y]lc|O3V! R zbJ'PnGqVJ"19WVeOF埜EaEJωqCN5Z g-9[S<$sUK5b|7sn\7x qmv##FF\ w[=-43$^ooVSiXօv7iB۴yg>]Vf"r$J3""32!Zh[K%7GvNLs+4nB/B{vlsobJaҺJR:0g%&zR\ S3T[&ִor*ⷳc3ʊO[iozW٨%$gn:ܶWwFBԹjHP&z u&F2\f;ipW73 [; '_̽b;vib!oec dC-tS__$Xs]l9&z$2/N>%'[}b{h/{`{Ji׉׏ YJB/X%}.|+{(S:qz]4_Kѵo`^tY_4S#* ^zvݾMr+TrkQ g.8Ͽ^i>ӈǙvix>$o( ^qt*&t1oJVu-ql5U6jCЉmĻ*"?JT=K'O/|=Vo}l0b}}f?X[?/\JSBe,kP8ETJ==?.p5ފgbU9}ǶdNKk—_$8̸͓ۍ8Di\BԿ-1v{FF]|.^ۅ{vl12׏z7-R7wE?\nh\jN/Kձr_oBw"N QMBZqe-m:ӨSn6j4%!hQ;sv'm4kcM=!8\m[M4{SMliۇ%eֽR&N:{2A8)THLK3Zj[jPBx#BگMf:G1\`edcʮ?|w(-̮vXt,bW2;.ιNHRR#YwTM"<;mk\.foIDjmlJ;vxy7o7i\,KQŊ9d^Mmgc L*.T6tLeIuOH3SJQ3=F/ʿ<9\JM6mN6=<{xkP!F1QR[I$6ُimXu2An2yԒMU q f[IB-'䤯jYm52&JG\zд\~vdg QtHGXw&1Lw+nDEdC1w|YJmvP)HZ>i0BPβә?R:QO["]I_Jʏۍ>QKyu^bycBq4lXF~l [\*N>-J6,Gq(Zr5h]CwYӤU~ʶߑ u*SIv%ZfJ7)! FS*s_\|IŸZ)J ]ܜi4"z[+Z,MOZ))}|Ʀ(RUNIII.S'ˍO~˨rn}M)xxӕ0 eyҵ7YMAB]ӣU:/ѭ*6bcwP͵ "+qēVjŹO|GtY4V j[mLV M -m>",B$ GD1~j6O4|LxnNmqATNR3ε|DŽa[fmn-ڭ+FiK7Pcm;r5 l8r{#-]'nrFh2ruycb;pW=njRqRJ(d mnpckNnʹ+6]tz~E=ʕ l ZZ5jSi3#47.Lcfe`9؏v囜.F\-UZ:*0_<Νu9Lӵm&)_3\^ҹ3"1n1v_|uRʞͫr'iȧN_kH׺8xXrj=\МH)V\ˬ.Xʸ oVRC}ySU9/OBY먌5 ٿwޞ)rw8Ӫi5*5ZΗcGƱ !ZۄlmpjJ -l <R̵/JAպZuq\IdUS 48wXJJtcg4cI~aqߓwŷrm-v)G7yS^7H^-\mŌAq|"m9IBnF㏉9[N+mmy/!KKۉ%n +BdddfFF6FQRN-U5;Sv'm4kcM=Mn)\qιqUd9F%",6MGdT%-+~ f%+y֛^3SrF>6lc(֪vۊN;g._0Sѧ]ETWرkQKzGe9ʨsKA"yC y2\[5 rԭ7Gk5Mzw_4sM3hxЊ'oÍ5jsub )ͪ~tR2H]R͍>̋m6=%(˿(Wrr-܅y5(ܔJ޺YunW̹븹NsqK ]/QR#"ZMDfD|43Qw|._ԡSqTZBg??O Ϥ)/E_U|i}2 9Z?¹0:x'3,whǣ?C y-A~=daJј&M?D1_PS+Oi&;a @;Dž7[ zZC"bv:jjMQk$M RԸ3uA\=wI.AwC"^.{?-\NSiˏ"b}T/}q/ o.1M}R%:-ZniʒL$SgrBW*,Mw'N\ɇ{s\j]VryG'8f`}'N<*/`U숻z CwHq18J+vԕKss4R53/&XTt1bZƟo\=%nO)h$rBi-nKĪ^ ջڜlwkYm[̑+/QrZo%TQ;TLs($2C:s.%+eoNttq۰kK7O0m_t_pZ1SsSM7"mevFZ[w -FJ*T*jФQRg BSu|]g:ɵzjqwmltL.e3sRMچkSmjkmWœިm++¦'tILk*բQ D,PB\lI[9{%Gb R6öۍmX-MaʉA931cs..G4CujQտ[9 }G-xwl)IQz j Ó"rqe&=]꾧֎c)<kӳ+0JrRR3'TnXi^xMF Bު*tIL.[h"2"nKzZe'ZV/RrNYz]8죝n]Ķܩ>^Ժ]u-7^\mZjܣ9+Rmn ߑv?oꋘ?&ƪy^N4o=3-ؔ̿*`}V݁ ƒPu8%$ ݗ]wt;\y\>='OjPIp/nJU8{϶FNMsf"ίNqƹ(+ ݮF2Km |jܴZs%zf*eȫ?]4)I۵nR&FX + [jDh(#哑9q9Eծj8noǕZf\J-l&Z˫}`ӎhyrΉn\űn]9pʌӣ"׮Wt?N4_I_~54#/my1Xr*척aS#DT >q ssΛW;3oUaJSRMDgQnt:Ql,/ ܷfRqiM Ȼ>Cob;A>ڦWقM9X~/!'MW.}Vrߔꔵ!5|iB(0-zF=}okڢE$^wW~nokY߮\6՜̌{i-AF*9)\t9IV6۸5ZUF6R$ŨQIq砳YUZ]eyv >hI櫥N )&l JulwE1GDOuFN2| }馥uC1rޫV+^gdb&W[4<^e4YW,d|htͮsUM)۸8:{3d{AѢ)~ \#J=NdƮꮓ90 |1K$v*?мS ]i$J,C,SG?/_՜pMSƯM|mG1V1$~K>CSvkuj=&) -,yLjuFHK{c駗.SOua;BrSqj-ۍZ#'Jys7[g2z/.u4+XV2VQ.ޕ)$"(%)#Z7suZ%j }BǬݕe)Jvz8zJf:hIN|svO1O#IEcۍjݽ:SdὮvu^@:o^5cs>i/VqmVm]ؔܢn6'vޑ̗J4Wn@OlKbX ;n:hgJ9ŻyǑz8f܌q&Y fN0N;[69 rbׅC2/#kE l&2~èMR.*%g=Ft.%؝e8<.e=Uv{~㻏"EˑnvDѭ͜Lu3u0:U֝$[M5<:oi+V4V9 6nXvx&_ q Qqw3W:uϔ2yb/(ɳ|5zQiJ#r|Hw#.W?4aDŲ\ugWG;Cw鐢K|xg)##=O.dF˟jMUvWĻsr.z]kPc9"]R)mkfOd*uYf١RsB Aîh=k]ʳUrrZsq`d#r$/Ը3o^&lRWȍyuW̦Y4QDUMJ65ƒ[+ygk XK_±k#y:8(TJOSQhJt2.DR}"5[) r)6V6u5k:eXZmv𭤔!푊Q[qQ}ҹLE- 8qIZG|UM4j}Mܕ[Vwm{} Naqµ"ԈM zOpKѰ?IAD3Ir0'/q1itoB5{%wkOBn-ۜduqIzYK60{+DʕܞqIt";r1mG/\/ym[6JƫR \L=S=OT@Ix[TMm{>ݾտ֒ݸӉLYIx>+"JVNzx||5rI?C{oz8۹e\R-^\A2F R+N9 vlT]"ۭ d)t֞i #E2jB@׵=#/N+!ĕhx}I!cM`ąZ*ŻɄҒ߮Y.Z}='/oۙ3IpW̮hT7cTSuz9>B}΄&h!>lӵn~j˅IvU.'v'CSZw8QK3G> ,J59ٷ+HSg䧎hJdzvwv-cvxS5[̊n~ؿ%ַX?O0\6ne 6kn9.ϯ} *h 8_QhLݣ7q +=XBҲ5?[[)+F`=4 }B,sNg==u*Nj9k_GJ)+R~GSPBȒZ:(K]heL=vKPӢwq(NrG^ثϣ?#tC?.ͼ[ۅo؞y#%ǛjVyLSw%T*s92JTM%"YkQО.q)gCͲn8cgi6j1MѾ[{9h^vƘǚםidfi.^RHmg&rׇz:}݃}xT$ضk'5s-狶,\vpbPD،=Okf.c#cdz2FK5T!&)|ntD<+OŹU i-G[EE*FDfeaf2QƤM\UG_{ǹm%\yrGy:.\4wjPGUJޕUV7Do\7Vy_13w;[?c]H\$IJ,*L]3b%L{y.JRKG2sq,B6T}(#nW|km+q5] r㪍bJ@y{byz,b踊3ϻJ,'^xd،)JVw#.Vټc''ÝպWtbRؒJz۠8!o9IۄS95E9ؔ-e9JR{dmnｯ<[~n${~Њ$W?&ՐY_? #a.ߑv?oꋘ?&ơ|y^N4o=3t=~7!/M3>n8W홎2M`Qx+ z qy8%]7_~540ۦ彷]Wq CѡwkďyF5Dum_}~P(5.(X,K9vᯐ?leB9;Jhm#3{CxGE-S{;@Fz˙]=O'!ɿ]' r`:7'2bЖ>Iy,/eTy/V<.H?UYY{\^#ѣr9^7?xoRȆ7EoS_&??zϾM?(~Q-K&>"~aߨ t7Emsϛ+?;fCr)fY+>z$tIkjn_>vnrֳki-˹l= t;'EyC¥|/BLwBJdgjۛ$s S1|ɍV%JI6KvəhzIlBYɒ|0"Sy0F>eo5W)O+X˻u';v)2vVq۳kۮws?UʑBǴYO漪e2MIjPAک\b1)DDؚKm6ZWΨgȕ۶yjڳ 2ضN[C[|r@9Jfo<_eI7q.|cÊV߷:i.:$ȋ)1%%)ADZCEBxJ0MJۥy(bNsKM9k43IwNt.\%N簤I'.j|ƃ2$grBEٌ\}9:v*!n7M(ɽ]7c@XxƱԨ37īf62cTTfFK]9wntQHͮvٱI/f|j=7}\_V5U^+:uljSȃY(XI.ȱmo1甅jڎIZ2>#\*:gY|4k\8ZwSqtyA!+];бޞKծË¥e)#5ap.QK^8VdU{*ѽL\=qmjnB5>{ Ӟ`v±5 ^k&O~Oshɷ,;6nOW>u6{RqS`)S%jp\ipdEBLfTWy$GIYw~䲭J.1vSY5z.V>^+Ǎvc.I[R{QsNR3ӎfhd>y?UJ*}~[e\i5U^͛E]G_FS(Iɿ]i8:4zj~շsW,ˆsy:%O}iur]iF5~3M:Ӟ#N06)4ߧgdawIotiz:1r5YDZLHBSi;NQc44la=Y kQIT*ըl:tq2(է9VO4뒳܂~2rq'nrVZŦ[t7\oլfb/mlpc.I8콚q^1iE~䰳mi[dۧw֤ICfdFeCsg:i| 6擣׋* 96lust^{%99UNRvaMܽo ammi$em4D6DD\nA%$$#}۷/ݕr99JMն[oT޲E"KTaP+HGkŴj5TM5xƱOS-k`ۛkٝWz;{kS}F;~q|~^_|euwnE'pSupUP)V]vE+t =ZRaVdG6= *.ϼnj9:UɷbېmF_tޫgHjVS'śǕًdkkѻ_]Kv?nT>)^e=Ar1'3ԔILyD?:-^in):{7.؂\.:V }#뺾.3r̸*xbFM aȵz 6SQ:ײj[ 8nn iFMw rR"5M5I旘35f^j='j:nNW.ʭocZvZKV^ɚJ.cM1ZI7E'6rg탸5oZ=[m Z`\hbMUR١Ȗĉ):Jin!_7Dй+f̷eKҷvͨBPR(V`y6tw*MRΝcB.ڭTnc;P$8nFvm4(D(R#R-L -2:FP lxZKQc6I("Km%$E, 78uXIFA$RQI$JbInG]c[ֹ:ZM+n^')JmJMJRu{e)7jQDw~%yQl}BZujSSf۩QZ+Dzhd5o%BIc'GZ?}΍:>Ɵivז-%݌J5MqGWTVʦh݇ܟ~Օ_6 n'{3~mϬj'J11OȻn߃r Qr\3y٘+WӍ'WxEs^O3 o~[|7>]]H9݇ZomT@]?5B:Z߂'`V_+/MSKX߆ޠk3?o7y:4R/7þ] iG߬aBRU&?r&/} cQߥGj2?C5Yśe7hU=?+ x龳f-܈czW^7p%-(\D4h{UK&ӡn^m]Fݢ:`δvj俜F+) y[{{ 7 tu>gvrěOj'5 iRg[ͶFjGe n~qT$ci ۚ0oԹc*jL[sVWqj\ݻ&6"WoK:cnWmrv)o>66(F>=W^bf#c zzʞtپy%mՉPël e}J.\Zk4ttt>oEM=q)hJjI=ͥ(%]脼_88ф;͛gWG;Cw~˘$4=uWdĜTثNDkiQL9U*O"4XP`02,Ge-k5$h>ܼ]3vr6!9RQPIVSnM(ۓ{>;/Qͱv{3&-[rc)ܚI$n{Sv3[j00)-D3z}MRzVQпj,T[uVs0\}Sid;r(ݝJ>æʺL&c[jPK0~d(FKÝW\m]GTcF|Iׁ)I3~#oX%vҦEݑؼ5Żv2qAZTE^..M{ʐfȏ2##.R}*KʛZz^ӞN*lPťLf\G6[WVQquV]XAi)5J!,$iJ6o$tPZc;Kjx_n3`qIelV~vLy{fn匋Ѿn%;zV.n'-ұdd2߽1bZksPe3TI9)$ԩIN9Vơ\=2885N\ p)/a柛w9g_lױo8ݷ iixJV& ғRi{N^_oAŮE6Y7I$Nk$|Q)-*4Z)^¸%4Qm [I%.c-OV+C֧R#%ѨCe3i;w$G+_dy| Fzj$DI(=OA gj%v/]8qԯNIS*֩',Q%\44ZZ%D|Ǧʴ6&vֵI$%8(ԬƾS&#Z. }6z?b/|Jl{ץv&mpx4Z$”ڝ4-H%dGKfM:sKSRWeJAn]>s6应-W9'H]'uȫYvgK^\czp|My\鏩w/ËQ.)]\QiS`8uL뚛̸=J"ܻi\å'-)54Ue]:K\퓡vK xwBqrH\*֕TnzC.mT=t-H]SČ~Nu╏NÅ3f|͡G~B+Xm[Q7U{9"~jgK Zoʰ7"qJ,ekSeNGgϳ] ^.6:s}_,%eRg<5⿨z{ZPun#jRІ.6g T.!]xa c#jN$Zpl̋H WZu8WmMRýsĮ?Mco~sx TU҆Q :KDG4n42.<3/'^?6/ܠڒ^yrrÿr2\D}}B]^E~^T cɛ7϶Y[<֞[7d}2%QPqOLEQR\CIsj1?\}%tJ0e~ *sk"*)&ۓEi#{1J8Hrt|'ܝRr8)=ƔN'RVz:cf]F7bZyZUȘ4x8,#JG̒?.W9XnO]KO]%]ƻ O5Γ/3qÓj؍/r̺rƵ 5\&m6h.xoeX[=<3%< lZ"2h\Z[&jW3ejm?k&[]ųj+{N{66leu_+lj]q* 7g*knأYv= q ەdxЬZ|%GUrQ3jLŒqET]1% qkXYūYc[7Ś]QY\jko\</Lc7+'hMSUc6qXyؙ~6#ѯv.0$BQi5YyIhɍiy=KD!n3Vm[V%W-B%swa97ajۗ m+9~]fKq|Ddaˑ0A]_v޺mM5* F-BYHJ5}q>ʉ.6hyDmpD׬'-_v5;5[8K[viJ.3dR:oYHHh9I7:۽fi+wm^ [)odPѱ52CZUJicSw\&_s0uBȍh32džzQflcd^m|7GѹE!fO5]]H9݇ZomT@]?5B:Z߂'`V_+/MSKX߆ޠk3?o7y:4R/7þ] iG߬aBRU&?r&/} cQߥGj2?C5Yśe7hU=?+ x龳f-܈czW^7p%5|Y:SJE\U-(a_cƣUǽXXKiȞNlmۊڭڄR!**ܤMeȽ$|X5(Ź\rJ~ܮ]>'HB0cp XFr_c?f?7<ukSgov¥iG>>䙗i.+t+bOjIܶ . i^:nm}s}(3>NZ$2Qg([".>i.ƾ)B̋M8+"- >eE6DݥJnJˣt׻ 5.˅nJGwZD~!i۶a,Db3ZQ3O#KO5/֍ozuK'GbRi᝘NV_ҝcvם ZoX}F6z 7e5_e:ۓj=AB+iܔERadMBq*ԯ DwI/Gy*mĥiRKg6skY/#SN4e$-yXM YL?^ĸNNӪ{$r1JJRSLO]Aqm>V/s[~i/j+m>z}eI"Qvp]{ZԼ:{vPAG2=T͡@ڐ#u"E*>C;o$~C#_d/HBq^YRٽzIKbOm\~żjFFGdiQ(*/i*#.FF]©m=BmpQQQSP&Ҫ!T&^>:y)$ˑÐFčI Bӡ-t!bM WҦŶ'UZ=}zvn~oT/\ǒ'nr8 AJIӆz<^uߖ4eFC1i+v!3qNyߕni?4JZlmYFXFۼO0B\m[ tʄU3s"Sr(NJ;SKW72L4̏BVdf^Ҹj\]ȱ۪(ӷm?J-KEmWڽ^4<8qu%9pŹW~877ܾeVгS(յe^C]yX͹! םm4FGȋ\y'Z FX7e)|Gjt߹#gb\ŧq_([R8[qU$Z (ʻezV2V!iQ,i$JE˂٩ a(GK'O{vnBvryRd-RK4=qxZJMl_CuuIz @Rt㮽޳!|68\-l[џ84-2Pu" RJ_^OL>G1~XnBŬw6J0*Uvlږ1N G1q9IUm*'oWu][&UyYZbBZRZNfEJf"+2nF~Eû7n1xv.RUM$6 lAxSQJ&n5ܞwlEói"#>4׿Q.nEq7Oko[1wg8ZQwZYiqtm&~">Bo?w͡ni2峋NCEy Ҕ+%ZJ ʩq*fpˤl,~^Mχk1+:ݕ z&Y`KLӪУDr3[*Z :(SL&ݻ۬Vqsyԭs x|iI߽zZrg.:mp%6ԜvgmpIUt;QbS.Է) ǨKSV,*lڌ|5Jt3#NP.=+OZ~/G سIgbꥹJnl_DUM\iM!֔wVZuԺ,yV.Q>f v:݇WiaŸN5Ҕ[M7SsrvǣrMW= \8ZW-jsnڕ.ZnF2qt ً[ٻޘY۷Zm"Jxr&NAfA-݌to9s359݆mZ+N1-qS$D=17 x׵+%_ ve4ir6Z$FDڗnFtOr'7'{9C˨ꤡaYoace{Refnft RR"4%ʌm:Sj3)OdInTO>X'vxV#jܮw9Fog;5.~Y5\~18YQܹvj4+~t7S ﬕs %^۵ڴDZV69R^Y+rj$ԇoJKR5wB9C>Y:l+EǎS{ʲ{T6Wi* ^^9k/y/Cs\g*qڵgn4T8mERr|Ti+iPe;;.i\EBEJ 丬i9ɧM-ԼsGDrZ>r#R>~X9y4b棇9JwV۔%m(b[Tjvl}۩~nDԺ{Zo-YuK1vx.nWuO+jN [ٮ0%"΢CdTJK-RަH"$I(*ve &҉FzB,_Vpqp9m8werv')E;o&QE׵^d9˦j\_,ڵugZȻ̧8k+jK{wmr@3ӭ2 wFkzFVqs1؛.v'I%$[iT]D5Dl2 nk7qUxԫLS+sا3/ΖeZYK<["%-g/kRs:f3;*E ت wJ%)5&+&rw*霣i|sMҴ|;R+fm䡩.!**dӶ-6s6,]zAXMWjmnz%SJߴm2UXw7MQ%<!tKys#P,W>s;3IYwx<+i_\\\U6 u7P|xbn_k&ӓVOe䦒 VUr,-㘘"-LZeOSҠթrEvq8Kf%5%&K"#%vD/.ZYYŏ+p$nZkvއuW9㓱Z G wYIFyf)?ƎUm5ԉ/'k84{KO:rQI}XRuԪ|*lu)3qZ[mSm5R3".Xcَ5c®ࢫI*۳~wRϿQWޝ(EJrri&ۥ^ʶ齲Im|[yb;mnm֩uiܘq>E+Ikx߄3r33-5𹻖09ϖ9[Tz~mr5NsWl$oPusޛ^{Z;);sڹf\3oٹZmԉ/'k84{NO:rQIBø8Bݱ3n֤DiK4u& ofSȒܩx<˘|N0Fչ]qsp"}! QWw@t4ӭ+cO5%]'*{eM߲DRO1y*q8w++e!c߶ܪlZWّM欼 CQ̼빶lX{vib/V/ ai;x6~]+z]MWB>re-:lgk}պ!#9?%܋V-c[z!W?c7YNm/jRr[HOzԻefճ0q15Zp#rkQQ0tU-AmڵP/cȕ?0cZYj;:0ZM=D6g ?'UN+ձ[K ܖB2'xq9{|۫N0ku 7xaj;n\ 2[VznMlWiKbSk))f..)Km)&bGZ=>OR܍W:j'rM'wYz&/鶧{Sʵb"vջq[I-ՌZH._x*BagC'T(Q:$ͳQcMCKy?3g'ߝqnT);qs #ؤZ}OOI:cfnc8W~qy.;^pVl]Hԓ>^H^@7-AA܃nmL(uWܻS߿ Td95Bdh4t6*dDh!EhI[iŨ\L.&Nc ܮf^;$R)\rip9I|ٺ?#R.ZDZ;/]nݻqs\QE9M&Bd ]N mN*D>tgbK>+ˏ.!23]BȔR1ɝ^j'k2ƮqBQq[$di]icV/e`޵B.FIIJqbi>Ӥ|p; 6${)RU>_e}^dzdfzi %ekRVUS?6'hׂ)5.\+qUgzE2C˷ecŏ^֔ibk shesFWJ#~> Wk~ݨ}ڶ>ơǚ)׽ZƉo~B-ڼrvoE:Ʃ3ۣK7+Y`WirS):{>ڛ}:wԨ(J_";6R%[u&ƫdZ_\'np| RJwNeTW,=rrbnkڄ[M3ܴz)3- R.?:okۼ0TU'w{6&w7j1z3ON'fGoO?)S_bQ_¿R(^ԴԴG.EtMڇ&RUiW uQjU> Kiu1d<ѥIQ'RQ1:O/lŗᏩiʂv&Jc{D5 Tt)1.n[n۶X}RjqnOʽ(~[Ns{ސ⛌uO,kgo֢dRNQȄ .'6W!׌P朼tdZjFGE"]K@'i۪N;sI[{SOzk>`rRR+!σj8&TjlvA̷Q?HyjyLHNտJMjܶT۽lG?SnKN%<‘ nq[N0Sq[Ta(&t(|HGO~gvkݻTR4&Z$#ViOY1r$6YF?e4U/Mvxų:zbU^gQQ+NW_'4jfz^c'#`rvrڡ(IJ/J ݦ6 ]-CW |_{v*_q3^DZ}Ic6Uڌ8p7{crZq5ki`)mU6|-Z5^iEz3P=:Cu7DF'k%}<C-޹ֲ̱#\,(f88%X-N(ck0VLR~} G"-8ӏ/ϰKq?(#nrVTmZ;zióM4 m |UT'C^_1X.gXM{%ʤd 4\ovN":"y-,T)fLQgۢr=/CƹǨJVr[a+!rT|%Y\ٱzsS>jͱ.oOc6f$q% ǒGo;n[];ߎjrk{~\VۓNIGn:iqxo |~t5)Rxעri{Vi&NUOl_ѮMfsޕkЄay.0P{7N((BaIP$ K"U6Gl ݙqJRu+qN$ m#*p<|{:>-Ev=86N*MM긭U*uѾ?/^o7;'u,h4݌xښRM:5.(/ \իU.{F^rmF-Jɷ.>Q"[4xT^OZ~mK}T0ݛ^SAo9u?lX(' qj%=X}"^e4wˠ|rܫ 6I\Ķ;Ӻw!'ڍWg{ i U_9Avhۣƾ+:vs/MK[ɭīe{`Zgb}r[i'GE2J7Nez579wRq+Un ]J.cJ4M:h箽Wxxm^ pc\wcN%'My $$| :$Fqɏ¾^қP9J6Wxvu}ݵP>Z'FFdg"-; [¢cmWkÎT8nG%ݣ7*\խCLRYZͤiD&J#'ehbSyXK|y*ӞpS̍R`[pTr/Eg)K+92{_ n3zwz'oŸۤ+sOj J:`T>Cf*lwd\fYOP"R E֢̔L4ɥ :;.b(B02rJ蠟9>V'9M%)IqnhP<%,r'P/vNSwr#w"ݨaqc(|{kd=^0jTMR2ULNz|.<|^PfY22##!,K~E BEJۜ&jRNsHަޛg\r,v؜.jK3)[EJ2ii{KEiHP^&]Gn8x=K}Wx/KI9-ϵwQ%spܾ[^R}S3$qvq8M[ ozKxcqmJ/ӿ{_}7&ݨ\f6ZSyQz& 7ۉ[8~UNn|nkiTB+4RI8'Nc%tn{!]Ȋo.nEmʱn𵵥J A+wy#+ikǒڂ;՛s85'KmE:Ђu""Iģ5p=БbTY-ͽڔ詻ngL2Q}$de# fs^o{DUUsfwӶ;s1T,ǤtޒQ\෼J=.tKU,7čJ5 N$y3kdSMQU~mO[03 $zAڟsF5^뜞"Կ QHmrR"ӳηer+ҔZ]hE-6Jmt'ޒ=O[sQj)6K}?e4v_KfZheޓ=BV[bY}lݒTTЬ{ȫvO_qpRApVŗ 6ju=*BR)g "O1yhb=tqJ gtm\b3RY+JQ^Ō֍\յ\>+uSi{=x ^w;uӘ#ĸzLn*$anok߷CBӷ}5Yqvdž<( "_OWit5:EZj2 B ρ1̊fi[n!HQF82q1牙nqnEpT(2RMoM4ϳOu ':֧_Xjsg jP^(ڙ{2%E͖j^}ZU[Q$'U) <܂%!s"m R'G5M0<+zM6qYm$ڕ$3ǧH]?o2N<8F1̻r_my[Rf59NjpzBnl7*{.QP 3N&^BLJPjAHCK2Q}$#~YMq8 k(MFMU)8MEqTy+Tʞ-ar5yܕOXw!e;q-Jqܶ䓊Y:LC UE{/t>r"lI9)3KJjϤA 6SEE$d߇3KG*En|P\ԭTn6I-ƍKTj<1H_zwGr19wF N8ݝ+a9ɫM6mhePi%mmD! """"""*1bRKrD"vnrM۫mmĽm]ӡiG~e"˩ lhRTMk^MX["Jݱk7_ޕ*DqĒ&flՒ}`W}~SմZ{ĕ~wm*/{{ѹ_-0ط#P]xlڱ~Tn5wi*lڪ (JxioϏbqKYR|!|KN53 OS222$jzww%i}>N)E+rۥ7c$Ofl/LNث\6H9: FY󡈾I)fB֔JI_ ֣^: 9mY{66㒢7Uj]:.-os[R&gMF3˸#໹kmjq^8W"PΦURjʄWa˧T!͋ lW48JB2ko+ /Nw QwQzQ ے%$ޓ7^YL|r7!v%Trܥ &|M8~ybrn[RV gSn{{*#2#ԽᢏӴHak" ӌcwҜw&RJ07ױ>Ļ =^ BɆ)v32.M1=#6%̠tҤnzqMwԣ~s*%-j|_m*.Yx9Sz=)qE4 3pk+,`=kNRڥ=B=nŔNAx)Q$ԩȧ4z3t#Z2lҮYn$S%y- JzGpu|LBV7ZW#;Wwipܷ%(6jFG5#{$D"uۭ~]֫SrD܃fҎӾ+Tu>-ZTQ& N|$沸ii>eRWݳu'[O̻j8JۻEѩ[]vni= ڒ,[_%kC7I3Nv$4ɎЈeٸoUu:[}Do5|zNq=Tre%ɧ6&~DȍF]ƞG5q m]/w/ \ʲr8=oʔe9U(W"|S]uZd#?Se[W"ֿh][-7Nu:T=)R}.;ml*5Dlf $fF(̏T hiIUU4Szɕ t(%_|2 ~6eM;TƗK[f&]LK^CE2[ȏBOd;Mi|cx,^6;sیGpQ\NuJIFTJ~đArh* B"$H쉩eXPRj?sl"ԥ)su]xpԴY%VESH"ЋJǰ K&5^Ukzׄ8kEgS2h&Se\ Yl]WҶp-ZUvi7QS:4byqOo+[̺腋[6-_Fo.6[7$p&^ _GZԸߍkc.qqoI[9m߸YxOZЦ1uoiSH)P9Uʄjcq= S>֙NeR><;+ڌk%_qT].srNO?s[=vH[]RZHRMtᩗVؾ:/~u)ԍdg%=edVrISb{6vSu=(ܥ)mTv/J}̇8 S3ad:^hBSf؉OɔLhI_1d8,L><_A0y3rXq"'(۱;mFNII.v5_(^q~X>y{3צ I*Vܛv/jW' T'NR'j%ꔩ:mJ3SB}΋!-H-RJBТQoedi9tjENenPpke.%4]#{:>mkEɱdYWl\\\'nRM4&U>?Ќˉk÷!𴪛]]5}UqG~ݏI"O~s6(Ļ)qO~h}uԕd}Q~G,oE!&G&/]_H-O=o{k\̭bkv.Ô܈+;arZx)m?M\3lU$mk-CFXjTv6u' g:Vn_*qk:VC A%'4JV%EY)#BғO4<e׿jQQ]yUr4=wm[K1r׵%Iũ-O}|kC;/VcݩWZ)EHdžTru]8hgĵ-;=>U_ InvTm_jBM+QiF"9*{DI/iuo(=TzϖmPQl_v4z>T*ȴ>YF;ε\t]EH4ꌇ[VrLzef 2T^V>g2~kg5~Nק;{~Z~W}&ŒBӿS2$J?~(Yœ"˲ߩ\O]: J׉ښT{mmIѩn3˧)4LdFZ/zUG>U> n 5& ϴ-KJi2o]uKljvK3$bԔҚV旧iY5.ίfi96v7!v))FJM4{jG~Jt/lUE%pTAFe4qQk\ve۽/u/Im+W')v{\-E|Pms7߮DZRr۞/mu*1ՙaB܆ -xg3#6ۥtRogʌU)׎]ZҞNnŞr}F1Nnޞ;cZ{N}ۿMiuxʉ*3qi'9KHQ$WJxXyرŔe~[v5~/jN9Q4o6rJv FrdxM*iRjMzUinHdн7ᾞS=S'7 } ̽zt7K|_g J=Lq+/Bw_\ۧx\HJUPzQ<hqF[V0x==CsU7q|^ {)Iq38$_A(VgcKu06Ƅ"%i~_ˉk QCܣB8Ku/񋇵u([w}$F|8TՠI.E !;RJ^}MɒD_q2];Ɖ{5}*n7nEInO{Mwv}&q+v [V}Ĝ@%>#dXQ$f;iep.GquixVt x6bj͵mlKقQ[T]zs/&yەnM'W}!Fp_d^Tu N{ɻ'l{խ2.sTu{W^H&;1s)Pӛ6>$mě;Łnj= fLT)>׸+qReɴ[UR\L*P/!$Ӊ3Q 'K=m~6XqW3^W+ųO_[F$rR*u"T%@O +%# ]˽!aܽz{ͷvQh쩎]hGތ5ɇ*DzJDRNLi 4:{~2FmXY-zzĽ^f=]uū{/+&c:Ma{ĝDp2m܍kHș/(--m_vݮK(V{R}.k&yƴ7i^4@3f sK3^Ř˸B=]?gt5KbZB<e;kQLpxuWC}n 5ҴepB##~q= `x]KWF {GfŲ}?G.I9pjWkU]>={7q{kO/^I3==f1ɏ%nnʫ/Zu_yXN<57ۍ'vy/"8넭M2eԷ&Y,в33%IkjMr7xf nmQkX4踼>a-GcIeތw&U=-:qnW)z¥j :WqSZvԒ#j"KrIU)%qrmRoDGQ~SYRsu*V)  ,/x)MFD6O#]z 96[Ui(JRfw'y$GeUީkdMF-ݻ98F2d[o{Rn0n-xsV6Dh|Eb2E:KCOӪv4SJCr"J!!m,hRLD| ZYFm/X~ΧfrN&4Ƒ=Z9Mh.Mܵw/BdrܥniŪ8ɧ|y%œ[M=_tj?F!z5\evM:\ ~F-sg钬OWq“iiȍ<Gi%%n2rqͻllƑ)okw7}\Uk-:&fj솘XerV9yZuʼşdFC=rmo%~ZN78X(N)_7.Εn1MpJ}62jjJdI";R5&iLԸc:jmqiQj$ujp\{;v5B񥍪Xn Ą4qOERjzN(Ga٠䌡)p*v(J7#ZۻZ8O W uONb+^Qipv9GvֽƼϯrYƖKGJQDNPhRJjᡧC"21"9ѓS1;R_O7/WGz)8fE%F2ukmvSov/iZ&/]~KmI[:^~ͤ\kMi稜\ywJt3W7 8Ʒ~ݥeFgѼw"8VVSج\뻆}ݭ/J6Q)d|)zU3>k\L=;ow֯gN3pKѫ|wmkZ$z^2R:E)f>ς нd|#׆?\ǔpV{;\$ƵE%-ͪm0S6[n< kE[}mvE4DDZ^$OZ0*$~XUv҅B@^?]so#%ojw;Y#SxxueBگy v^i-)s)zV jC{7Gt.w3v,ygg8s]aE_,*E tY5k٨h=o"m泏:\6w噓aiL׎n^c\75AGkЯ0Lf46َ`egZ˓p/k;̛]kq!ݸzpԭG"}R9Ve>ˏHUjJ-&7nrnwG*Xv\˱/vN}O)ʼn&CV͍f̵]r\PMB-6Du-#RͰtRN^)mT _}nSȕC*_xBuTkJW[`ɩ`ejvsngP ڻ.-WUtܑqԹQj)t;vN&RNũT+8%IXӃ5fK՛-d9 ]CƑm|nZ-6=Hz,*aEm W3VzRšdY~Xf׀Xx"]s;)5u*ُHB BRGS6bݶؿ 9j[1*jױga7oX CUI%0v#~\-O-Ꙛuɷ쏪&5mY٦M`LJ2qK~HZbr =N'YobI. (^ ׾{_ ?OJ`S`3BN[}5w6:ǵ/iSlt=4F*d&T4y/#. ɵim5Uֲf 眕6Y7 fơ=3dϕq뚩$qTM-%r!$@A? ޾V0c~{[{;򥧅a~ڵ»&ڄv1ek=wb MLkNAԬw-x>~/r=e73VeVN)K%Sښe"+3uXuچrn ֺVzscJ峻m}vb㶓n\YbIUBT%*,0nov=;z꣓S/nSXSpl##k9mXGrZv^Gde!ŷRԠzQyjC]`gToPov{j~KRBMY}i[߶9KL2ԉO0K#m>wB[ٍ+n[[b٦DX ݲpo] [\m5qdT()mo4Oy9Ie b][wղmM~vmi۱~t \}$яimRk(L c Cvk7r9_r1 ;zv|F@KyZ[&jEji/"6$69ml#e]9s\{ScL}Ȣؿ0q/nZ*t,CLoD߉Njǚy=Pgmu6^]l-["çUʖMlʍp-"qmU>۷uFOJ%Ǔkx 'g=睋k[3u,{³WɘݪF]ՍeFX"Oy\,cچ=w/gn Ļ]#2? vqy-gXnR.^}ݺFs{ŝG]}e|#0mjx"ƬWكm?rgU^xVB":Dt>@LRbun~ݭ,w+v⪕;\U(RYa61>#Jm˞Μ9g9XKaG='u8gf}'qy#ɉw J]We.ʲ-<+&q%s?2dњztҼn`cΤmmqMdz O[-ߩӲ&;[tmܝVnr">{x<8U+p:Ig]zjGkt,uzf}dؠoJaکqEq -(:d<պ=eKy[˗^%ZXkX[C2߱\ITTLGzANM￵i]K>UsOGDDD.ZF6* ҃V Zhz{'xp^`wo8r0h ZmJ5"jb[l=yUu7-;7IT%:jFjߖm0tzU'K)څNۧYJ)4IQ}^KWm7kSP>q;ނ#)'n7&׊r?óM{IwR\j2Qn[v pe#/tAF\ϵ225q֒om6z})6҅*oqDsMf CNIN=T S2t,_ѧ}kveMF0J\Rnnݙܹy[rUc-j{yGtkQ%s]5qB.Nw.JN1LvR Ui5J ZESQԙr):MJ+g}χ!2;q([jAud][ljVK3$ײSJI=/|&tl'*n۽f.frܥ jQO8>&Z];.|7T/C}$ڋUmP2Reҭ8hFF\L 3~e v\۫]ݝNmrnB%*]Z«hKc=BTLG :V74$=Ǘy+EX'4tn(I:Ѝ;Df8c,k1%dJ6.j6ź{N~l6&*fœI7 WAlGOu-ҢH,,(ǔe뿋쩨kM܍ZſgRvQ' 9)?n|er˭|I|-fGK.rΛp8XV1%K6mvG+tc+qE&ǸC_Nm:l=_/m5^[dߌڇ.c<%:)tQ$Ow~-aY;UJ>=F)2[nk؆?훐M=l6[4(O.]2#-H^n#->&mp5~Fӛ+|| S,xag%qkEUzUgæBhߕP(7]kFnq?֖CpruZ6*rEڊtS|*tI*E}7R<,nUU֫^I7Q*mSly%rdȓd8hE<9oHhMfNSRj[i7D[Rj݊+kდq{"$$H?p\̅S?㭻;t~R߁)^/>Qj`yt[w ԛ;²~+ߔ_ YW~|o]?x^ᯛ `ʼn;g)T@vWn]>&4lp+$D̢1l|ȨF%-}.9[}w~ ԠLM9hСablfe&QoW!s?wjLK?s7yO>(=C~_nyǜu?v3vyo oI@qV-jeES^[9WoSܝh"l2C1a͔CiJ@3:Pճw=/7ovuk+\V;lDgն<[A+rX~d;m!_s8ݖ׷;;.0llUC+?i#_crʙ1~C.\–q ul8Hܶ2m`ܻM3Tov|Bs rɵ"oLS- DКw=Tv@f'6|YlD͓Y%׵-#Ѯo%:&!3o%\J<02;K87>^vgƓ# ;ݝmz^Y6=PS39U%~ &f# }o!muH;ʲŇ˷yvP+&.7e[3'vR4Yj̗IZ`e˽3o[WU{ m[sUbۋZǾۆl6~9'V*.\S2<Sd*zY[aŶ`]C$n.v^Ʌ dng>ەZ,Mmϑ :n6nϦezWqUJ4! ۇ4R! =>>Fn|Q[{pRO17ƕ~._I''00k=b՛o}Osðc2'o\3}ݭQ^2 . R1yKȣtAݿ-uܾw!`?1Whn|gzUo[ECWwjUIן)^h#1ɭ!/Z np;o;ΗŻkXs."6E`Z1 עӐ9Kl8qd q} 2Stt;#j>;խabONŗ=fwP1j)l6J̶|gV2`y/0E˛6+ԫ1? 6}KW c\KoKͨ2ۅFw–s*TԞLיuDx .kCzWXhy۶gLu|%TnupǺl-S* PRaLnT+c+*xl.v!.U=|; !_L̎뱚U=4hm:ٯ"y)$:>%(n}X'p[ȴ ^˒4kƓmzDx \ 'NqamP7nyN݅=j7%McSڵj%STy qXymvCg{w/w=wSW5r̹u erծˊsOm=DhEҚRb#n)QOxtվQwe]I}wCa'"[ۂ-z}2UuKP$㜉ԧ:mc<Ý>RoL?wu|%ҷ&K y_!y9 ??:tq3(UU-lkS'ɸ@jdzQˬR] EVPW1DJq2n:,c|ǻ̑;y{X,ۂ.u.b˕u.tKBjQ"[S園S`ٮdNبeJ&9Ơ ~0a(Vm٘L+Jr*vڑE( x0+tp˕ n';wm-ޜMOxX>{#2%jgb2M[`K*\5@8l'e=0u+w ֘鳾{y܀:R*Ya]"Ӧ%ktynlۣ65,3gU}{GYrb;ge'TKwǘ.,rpܚV]Tr,!dp /ԺU,xՉ>s׽~W5oTh yx?xrrx?)?ilbT׬,z$Ԏ.UH٠\U1pU:]JwSrGZq8àd驐,N67QYBӢD㏙W!Q25ϸo9ms-7-%3CihO.J鯽-;MZM8ku-7k9S$8]q2E(}bۏI[DKOK}3KUB^u %Y,u.-&f#]'܆o$x`Yu,dzwM;#oKxn;\[d7}Rb+*Y䛂ZuBӱl{j0O̓}LhK;[aֶaGL{Cb#S.T[>߃F]NK"u^LUʐ_ykW?!GRj29͖qa'0[npcDvV)qz9R)PۨM^aJx W] r>];eN3vxdmĘ(5W2K1䪖weF{mE/QP6\u54x5[hۮ-Nk”i[lUgL]J}5 S:EhiUrgHl!ŒJ$pe=q^b͵Q' ?6|R\,JA ڵ"TDꈭ:ymg`B5t%M] <N_zv2_Ortٵ/i/ReӮ*7[qүqEG* m"[I:6e^p"I$jԴęh!m)]GZkcjS!{e^z}+Cѥ9;R|/ֱeiUԏCNu2Zhcٗg$ݭwvr P8*7/Lk~I'Km1+MW%Bk|oOm>-#qj*|Dbѱkn|n{v#jĮqNpMIUm(7Liz;{ҜݞڝVƚVϬ+sO!OstGvxӉ']uӎ4g_ 1^-8ۦ k!)Ύ5O;YSB#2Zzχ;<.ֵOtge~.(RC#wFZeGZٸ6FFJ4e2ˇpJT$[wgV)q6muDGJ56q\I!̗ y/I~RtJ9kJ]Iy*'FN0s.[l!fw'y(7$œ WƫgyΙdMEU JQJv̋vmrۖ.jWR_M֨djYgSj0^\y'EoECjm$ IƩK>Z28J2TiJ2N#}.s cArl嫶nB.FIJ.)۔\ZiM>/hLĸ=C1s[?YMqp|94- 鮝𦔽/k^#NT(Y LS$6˩}{;5 )B۷W$qpN)qqoot}ZDVә;7TiK|6f3h$dԄ}fqݡ>Nb򗉉+ͶO]>ߡ_VtYf79ڰիF sq~prս|QM)g%l0ocJȨHz V;Bb/kLAcfPJ,ԭ{ƍgpjNR6VSI*$!yV足jᇑ.](EܣqM\qJ2eZT).<9UB/(B0j)mtKEj#׿fDI-=rZړj|'Nڤ]k*i$5qt"ݙPM6E4ke^Z8ۏhz$Q(R Ay2zfRñnpnkbkI:=j &ΝșW?׵d{+ύM'??XqeeĽ.[o=UxFS=ӷdZwenՄ]_X=ĭVa* pKs0ބۍfJ3 gz̚i|wnxtjc¼5${(1fXQ65ȼb̶Zkn>%FQMJXӡ{TZEVNᖣimT/37cNJUPnP҂ZOE~"-Rc4^b- FEͧtf5[)S!OZIښݲ͑;tvܡ+N)AR=hCNn;wL16-:特7M$=Tҕ-.R[HٷnXk sn[ҞD-0WS9p9:-Ϸ-jѬNu{ҹfv)[Ľvwfg(ٷfe+0mYj8Q1\ݧg]Eǎvڿc!4#j5̋C2"}BRriFp7=ô\TZ:\BLfj#I22װ<;صZl j 6:l"6]۸ K'6RTѯ^ئOԓV\?$x7s#r:Oh{ց=MmuHԷd{pN /܅:UE#Yy+(SgQ(Щ)RHzw>^Ѿݻ>mK&^ '$Jۻ&w%F|xfz%˳ L~3N?Cy9 v w/{ƿ kz3x> sXv}vP"@WyC z`'톽Dw%-tt yVY\wmuPYQA0iG-2JP,6/gˢ]u.-n!Zw.N7Q]Df}Q0({a\@=i_X7gFǘ8^⻲}G MZ1)WEfO12G+=-B@z\`||w6ċj߬m}UwRox֢I &c~XGP6Qndpvܻul'V7^FJt^{b^B(L~sѣ6@߿^xqU!ڙ5|Vpvef-uӥ^3  FSDɯKD%0r}FF穛r7 +o"V8tv̖NQU!5uFd"bCr^bJ=֤fM#ʳԷP0O-9xRBm\=`r-:;~3Tl(nXtXi%2Vٛ#vwqƴ`L@"H‹qW.j,JM5B[)WܺUeZFqc'V˷1W7V̾-MHФwn8N;HPSdݷC7&2j.W\τGŎ'Vb]c.x+Rx1%C2T{myg[qU|+m:M:շ8҉yWd)ՋWS%%:iqlʹmGwݹ WnNŤѩ5(9hTٵDdGUi-)vSs2 2{OnT$Xck n:¶(lASLeȔBjμPpTb2~N2~%^k[ܗ[Jzs0ӓHBKq[}JَA-$dFQgjxxFv4r/x*Rm% `4J(&iv7SkԲmSH1YWmx 8n.k']:Z˭_W >ڃXЩ. jTq%Aā[E}amc]D:rmHRiu:uӚӢ\p(5-q%e)(۬ҖȽIf<߽pr&ݫVfY91q2ĭEQgYbTGQ&,yL+N$[q*RVۉQ=FuTܻ>f>f㋳8N6$܌n)9&»iˤsX,݅܍ȩv+sRTpO}d?Wn/Inpȸ%O]StQO|v5\}7Zwb.AIVK^:wb{[uݯcytO߶S<{8KSRׁH̏N7ۚ[xkwYy_'ZӵF+>쌛ZUĦreE9F[24De{}@:ExWs-\ǻ7K-\JNvEk%:s˙#κ].oͳ;լ7wB6nwu:$L; DkI#Wz.:Xp(˅v$Sq,wn\qIN-e<5Oe+vuYTpcojUI_ާP8 O 7&VL8z$_B-H-[uh]T{|8=qVRN-:Ij:7PUtXϷmy鉿:RIM~33ӸS2#׳GdŲ5+/Bx{(WzȨ5Y㞎#|˖+ ط.|e<o/rߔX>7s}VE.OVti׽ .5nNJO"95{#q}Ay9do]R"M6z\tnNS-D!@3N_jicWsy*5uٮRcWv/.,j}=S)j5C^> Ie =gu9ӛqjtz]۪TMoߧI!Ǧ¶m:,"[L!{qAv-o 3{"KʼnrIkfٶj2ƙ؄S`7` k6jzޞ?e5G&6uʷ2%ԒRKE*G\Npom F/V |C0.q_eenƣ<5Oh'67ɪn[SĽ{ڔjǘzs;~׌(ۂ`ܢ1ƣ` _l9Va6%UQWh~P~\F^ZHR@:ۧCJ{ôGeBh;~ۧnU J\O+n2 RҠ)ng}Kh{5+S×ܛ.1ZjG)iRȤIN 4%{oΜ/eO[Nffd ĹK?nnԼMqX'܌nZvq<ķbFnͪaQ`5 s,M_լ?-@_{w{ӺձJ}GF[%v\5[ŒGkOw/ΜM9rjË%2+rd~+󲕛C9U۳r[aJǭm|˒LAʨSCq[XMۺoubfp:t+ΤĻo ][ zt-*67kvS7D·MMCQXm;)܎n_h%]4ܙnRk!]ڵsDUF"`R, &#R_*[z*ZqFXɻ]7|۵w+'pFDەs=r./ᐚm3Hשy yD"jHCr':sA65نѮ^o1V/ f;nFr3VM)e*- s D'H݅fӧ\*޷[k<7u<-]֍Q8R h|p=WlW3s%Q %3l}@U-K6f-NϿu|ڴmWN׮[׸F*mW\%r! C78:޳vBG7ŵ.JթԚ2x)ST!řn~9 W:Wpܢ件{xf8ٳwKE ҰWxVB\qBZ 2wMb[lGSnyԚ~z9ZmያvoN2Afnݽjf>)j3 !;gOYʹK" Wftڎ+׭b*2ϻK>ۢӱeyԪXISUm[z+ugX%0lϏnvg!;t{BqPj>PyvR7Cj]O%+ݲ :qiMj6W}3vC/R=4Som]ŗ=ю, TF6U_-\6MyskwMr&Q\wjKܩyMϣUj0*}RZܷSdY3>Zjqj6TgzpA/M`/Cmл,޻feE[/+uk^Vs1W$G(JsW2ٰu*߻q*Y޵.Wi:ur5T),=0uRmho.twܖiYwrWHntvEj8qhf`Ͻpf(R&>Ki%I7$QӖm-2 ~yߗQ-앑/ x[k8nw.c㩵k}]FkbJl:{.(˩n0Hqvαp7 귎.Gupx[N`Yq'+ruU7[ү+>!xrȫoSo]OC# d^Q]\>!ƛGw^Mx"-+%vdX-:M2UR%d>%l ioSu6lsj7D P>XxHz Ukà(n^Q V>5cVtWj SEiJdznyej[lE' 3kuٌNn4JW)gB {4 j6&]' m-(ZMEz8cz>WZ6#7+[,MR-Z!4ܓtCyE|umj1ƽvƷV\;%>Q :#Le(iVz5 4ũۤUWxX ^(ҔsլB2w-V ^R+; ˂M\z+Uwr+RWY⺧~ Q*JcYSNSλUd8in=v K낫k\IRרSUaCFmϿ5̗P|u ZTԕ}>oYѲ1sfP+sQkX8Gb~6r,s>^\,mGL+7[n-E\.Fqḕcl*Jmjb5 ,m]c}NXfeVlǸJ5eˡ$4%g~N p4Y*WwW٧<8v#;qԩTut,m"#Y D\5V`\\Lȋ];LȇiS6ϝZ l>LruR\v=ǘϔDg=ԈdFZ+M{=|,[;0>RiSi4,S5}yxw&(E7&fݙ4UՕ! ~'Id)]ǽu2K-fޭ \08Vڅ쓬=Vy^^ IhyKR-B#Ըr=]mܻӾ'*Umkoy rTqT_i,/8Q^<ݤ|4ԻO(܄"'5N~#m.(Ҿ2i6Uev&I*<}҄$eNtÛzyWJubW^iBW.܅Wڮg]irO6Ve90sgv.+sV޿aޔ[p?3q*FutUo*eL\KM'EG*ZcAFfG5J 5jj=MJ3OK:k˝'NMB7m3uFҕ\-Ywg%PRqMIyZGY9|μvn߻5cWݷa^+X֥vnݘ\v7m>Fgzv"-;Ew֝}1|RjN𿊀7g#֟*GQQ|#/bo]p$>_Un9гUbn9׃ErQBU-^vDmVh'<R[fdHT]*~}3j;nvjc7s-rӳ Y8[n[1pJx kX[Jk9Mn!_Nю6x:iZ˦U |߉^Ԛ݃hYxk &U^bwKk.[jE+P(˞=9j@snCv7%c_7=xǁ<l {t'酚+1F‹l׭:ݻILruǶkL-L(K0L1&>wXB(pm;1fpnlp֓%Skidkt(U +xulo'/ڕeN r=^pZZ:Pnj8Hf"48ijY[ N[yZٻ+=  ø:3 ?^ܷ^Sr#YK[UF?CuhC b]GM')mڏsNrܗI]ljq6VB. W,UK"YX5{c >Iqā> T:n!,5l2VzCl|+I[*SrjnS6٨y+x,@>П.g+!rn9>N|W>OZT_ut Y""v7|sfި;Pclm EùN,{'fNT%U&LfH8~1v>Il}统u6P˗c(WV~H^bMU.o*oOF0N:_:6Smr_.b+|ݶYY غF,mwjv>f*>QM뭱Sd:`N{l/⎱;n-z~"Gze퇎J5S KG9!Gn;N1 ݎ h6m|S?ɂ5'WOÞ 7|7^ao @mxGmi^jϽ>01Mf0լD3-2T. VXR"ɥV Kl J O7|u?bvа;6.eߓ|[1bmRr,eRz`z 6܎-ͨku͹Fː dPhYgZUj}nvX;z=gVեTv_J }\1n7w2J?ޘγc\E 1Aޑzq;\r]]\Y&[nsNei\uURje*Qk2CSl*xJz-xٶlm+|UjUؓ`Ladqiĩ!Gd\W~fz;Tn*PdRM&T4`չSWq5k훶(N"Ӎ% V]֦wb.nUO!u*J&Oӕ2e|Z=eV쫚΅g#+/RW:طnbi*Wyo)p{:ETKؚR(RY+r웓r(IF) VmȵNB:h Q1ғ|u8E]{,'$-TR[j49l*3"I鯴zhd>Q+\BkNF=.$ZR4Nwհ(IpNi.(Gi33#33e$FXK*NdWrud[r{xnk$v2ıh+J1TQ[#JQl[tRO]LHKٮ NӍnF񨔤֞Em'MILB"ԋ%dBŋ+p̿_17jzT~4pc Vo\ƹb9Rq-'1j;8ܗ)hE%DZKS<璸Bu*%*Yw5ڻ9ۣ^z4U; Ñk\U(o~G?VUĎ:?P?_F_Kߤ~ᓾI |pr.Ok\SklRhҪz{­P .}SktZ7UQ4ڌIM8̈eaӊJZ%FFZu,KZvln廐SNFIVtuNi?CM5]+Ph,{jN JSR$IS^tSUVrORYu.9WyP6 [Kiu m!X|]Y79ӄ)\ģ)pbڳr%*&ꑶ_-H*dzk)1 V3')UAϹٶWRxe'պn۫h7AR9 EAJeGLms!%D| A 5]/Q3eb̄vnVn%za\m kZnv([emqrIҕij|""><hjJשvvǕ|Pޟs}V~2&Z?+2N&Z4w@)4iSڪ_>/JN9Hiۏuf8'It[ȲR.hZ$ȋ_Y ~U<UUO*6b)Ovzڜj\R̋.$FsQuҊj^נ䈈y<zZIuP[}Qm=C?zN(Exqu/kn S-FzKZzOסӽjJ\)F3b!r5ٝ|;6 o=-3*λ]αb\abqRi-w޵⦪~b8Kpo)Z=>)ғ"5/GTZLE-輵f7ݘ۹~+&+w/7GFI:l33fg.N~۲\2|*cnermnnM+Fq"ѪIz%j =YW8@~gc/~?N'?)«qȸs➟n=k" X“m֮VreMh2[uݖ] *FܖN)MȐ`f0 g,C9̑o;ddudJ=In13:ݒvvdMUEJLp^,6t-@͐9'{7m{-3,>hnF;ѰM)->>+Ěz!R* :`e--m7nB\u{b U>[8֪]6^ߤLʦ\DFNo$$dͶlgno8OrsQ\l̯hRo8tuNo+ CTxu!2[>ctFpeޓƻֶR"3QrQuOѳgwQr;S~)6HhZw/GgVTmUf_yt7%$];zLWF̰xy2Ʉu!MCmš_0[W6jf#a-KLi+3Q7c^qg%s<1aYIQeZf+}>;S6L0]Yu_h9߻<ƅpmiM$AVvŚ,*#t2.8Y)-Zhshü97/#Oro"u^/uFgWɺ,p:6a,^x%$Yve^3PƗMnTP&yS}OJ '덫MH^:rXԴJۋ/rI;S*,+yz1hv)Qw^ڍJ2oL׊q(\fDj:^T%vOadɂnS}ZO)N*λdaȜkG_PIEO}нa(^iQX᯦-7^)%g'SJx(.S9zVɴZ{E ))ۅi/s7 VIV-|sj0*UBTHIqRf>FP$KqN0 R̻8j\GcC}IUz\i 6F)Q{Gҧ3qSzKj-Az VЛS-zy:8*mNk|D鿓ND2u+0Yŝ7kqm·?8Ib]u>˗^_>(]vӋzv+ݩ){vZrJ2RQ몋C$z [,pp,8mڊbR]Il .f~d/ݓs㓓mͶ{mgjQwn=Oic9ܚm4Q/6ݨ[TƧ?nԶoytf{@AzT{e{[O'ZRZt~AGD?s3􌿂ՉIw'|~U\ w~di:Kޱ)U/sU%njѩ&GSP^ǝd)..!^U` 1wX[aԇSxoFV6_扐)T 2Mfd=ۖͭiZ7KK Bi9%7@<3<ճԻU,},a}FRqɛr i@ONJvK KLN M, ʖv0n-]DwlI-X6ܶ$Jʴh5O+mOI+Ra瞠\ MG7BفjYo1#͖0V`Ѱ2M?c8>-Crt*JkIGS:e#hPKx[鱼>{5m;wcն&>j-M֥^َ) 6yȜl_w{-ō̱r> U=]iw3)r*]:K]6BdCTZ|>gf}LW}[$'Y5 &c -j.z6R 67MԷFMnÌwI7w5E}o޽+K ֵy4܌ȥW"COyR[q5Ӱ͙f[v"_#q{MV6܍3"u9BK(41ӯqˇc${ߝCi6I(OmθzҜ5k^:>Jzw.>qV8{vU[ڶEm|DžBz].KHjI]x;Mɗ{m,qZXr忇2u^RO2Z}ZێS[2Jen!*NDcrBUً4<ǼMҲs1Zw57c3&ĖڻzmP*FuJG1-dN:|OU}ҵgi2t~F^^Z.VxjvŧnNNh<:]^~NN+ge^g.SԔGFe߯'[vn'(ScJ]kܗ7eJOlRrfziݮq̋S"\*U<*W]k$FջV}? 7g#֟*GQQ|#/bo]p$>_Un9;l S VvQU%OLU{οmU6bZ1MTx%!֙Q7, J=!3 ;Q,ڌ;6ͱ݅q^&ߔ·n #WbwӖX.HtG)N&d̵zpI,n cu ޖUj+VXUp[w]N o.J6Z8Ts&utxln;~HPHS/xw`G\ʡ¿rj Z^vt"[L:SD\h0sUwR,}[x^X,R2Vn< ]2YDr[SRKs8tXb̷G?Ps Tv 3be,zVz D[/I.KOEQrm'$7|[J>r S`5յwT#\w1FTz\Ԛ &"ׅhSHrD\'r]~/>p;:Piuu:"9ő=tTaS7V2rӷk7mb[^WmPp*[y.Þ6f]cizJCgRR@UVl큝.WJP1N{/\whZ ػϧӱE7|E֫Sί.x-Y&pi%v''-x6r'Ws*6=DwwUu]=C?MK [yrtܒG$!WGqJ*%SAz ED[^)/tė/g=#Omd.|^n/sl׉g DZqemqowݮRzUܜ=ڽ-o/Iۖ;qVʘgPp|mm;6zGl9.8pwWgsJ2qPbe}}UpNjٯ}7TMQKrؽtEx%v w߾8%|j;~|}pK]ơ/ w߾8%|j;~|}pK]ơ/ w&~e_H 8PL7:%ʭ5Kw&U2vwR_+rm'}C7#rWoO&HoG?M$UR7{FU]u ;# !Wk`|W>׹潇9Vn)6)*ҹ{%qV4q>W1vi#T"Qk&GwxcJBJ- Ϸ^ˁxkU}ԣ/3.;]J=<*)cS)ROK9H=,r zX @)cS)Da^ԽQ gxJI=w֣gf*TRj

2 School of Robot and Automation Engineering, Dongyang Mirae University JFIFddDuckydqhttp://ns.adobe.com/xap/1.0/ Adobed     ! 1AQa"q 2#w8B36v7XRr$9bCt%u&Ws'(xy4T5fH  !1AQaq"2B Rbr#u67Ѳ3sTt5v8Sc$4ĂCÔ%UӅFV ?_Aנj- H>>,m*>fzp"TrKkr^r.|_&]|*vPuܶvoQ1mwVJUhu-I"=LniAƕ8"۲ k*ҿ[yu:.vUQ+)%F DHyVBk>Hy8jݹ q~9D4KRmzQ)^ʔ.J%k_tVi5NTjg!'ky|5asOȻ)R۸ߩFMԿ3L4j6dڜ#NIwUF]JqB/(FafJRzq3\G՛ ?~\ 6)6W4m[O^L0E&rRMض*C .]Unl-1 1r#Rj/&QɈ׉˩s6Rj=5Tg.y.·Pӡ:JJS:C8-2u]d&vUz;7p9 5VnL֢"y)">iי(IDDd| Yj0; LRfS:ktYK%*N2^m|&dğth":ey)uPQZW)gcC3Pv&MMWd&Ŵ۲mvTRoժM03*F3Yd6\8,\hݻ kߔi<k NTwSԪmljj[>->ptU%'LR>&EBH$MQAUx[$Z6vi&_a.KIQ{hyƒ j"JOC9eFҝfj;˚Ω<[3_m% lQ@4g=5$(J]Yc-OMq<Ǎ wSzڗ)k$7VIP붾ͯnV+卵*t]iЎD31~SA1éC2u)ʼnQn-Uoi3:grI8ؓWm*G zܕ)ZקJ}Y YlGeJ6cB2I NS3Q>k=KTBT]W6+SOXQgGR? telˊ%-Re\hѯ2TF"C/OJΩ6r[N.0{SpljjX1“jOsӥ;ҭhe}xu`Ք&.)yO̒ Fߑ.$Qw;9Iw2o+RVJMSOj[SoҌZ%;`d$blQ{Ro{Imڌ>3egf\O֝Uzx"䢸g+mv%Gʆ:|V[N'&ס-ޝ'kfE|K,G&˳98Juin/\\Qݿ̋v~Ǩ!rtWU d|E߫R4d}.qPw*Ӭv5YEcn~f5c%MTMkb-F>5JT,})QHg%{("ӔȸWMsYyWNRrkkJr0XドnͫT}r-jj,Ŕʍ\Q2Ri>v$5!]"JB2WɅ)]VԜUc8i|.jeRO6^V.¸ Q&#|ܶ-*uOG%JAtRZRr]FFG\۩w+?'zչSѧt jz>KW&ot{7P&2D;&\\>Q2JzܗAKSfeNn[jRrԕf6,q,F1tRfԗ>vֶևj-&R'Zi2=xv~Elbsvm8=ӛ"ū񕜈BȩlWau[]ٷBߨF~J!|Ipr3R̴#Yp)={7:G{+:\W}n|Q#%)7^-h"Ƒq:M*%J&$T軨I333׎g_- ucBwwjp[6i25$̏bU’ٱRv?G\~#Iͪb7<<}Ezt" q_Inw,7-d,G÷%T* Wg1"䥱kq/A.,_KhqŒxwvo u2ۥۧ.bQ}XκA$֣ +K״ZUNmڸII{.v{5z5ѮRme[moyƾd~cRݾK'j.\i&/S6f|b=5: p!6i_ 4j6=.si˧eƾtS^c.Y^RJVS-Vi3,esi08?H$GvZgg?gi䤟2adw릿:"۪lkSN>q-4kI܋ێe̊qۅgDoѨ9; #T.Q;7#~_Ufstb_'w~Xw1Xk,vcOt._}v}8"(4Z\ۘgk?J?bm_c!g{HZV]Fkk%~gEt)b秴vΰB|꽸}mp~E6ݹv;7P٤v+ri*3Ԣ|'O14_~7nP{7ZU\Vű[ +7󖱅o#:ǥŬ\|3r%TJX]V7ez¨Y]lc|O3V! R zbJ'PnGqVJ"19WVeOF埜EaEJωqCN5Z g-9[S<$sUK5b|7sn\7x qmv##FF\ w[=-43$^ooVSiXօv7iB۴yg>]Vf"r$J3""32!Zh[K%7GvNLs+4nB/B{vlsobJaҺJR:0g%&zR\ S3T[&ִor*ⷳc3ʊO[iozW٨%$gn:ܶWwFBԹjHP&z u&F2\f;ipW73 [; '_̽b;vib!oec dC-tS__$Xs]l9&z$2/N>%'[}b{h/{`{Ji׉׏ YJB/X%}.|+{(S:qz]4_Kѵo`^tY_4S#* ^zvݾMr+TrkQ g.8Ͽ^i>ӈǙvix>$o( ^qt*&t1oJVu-ql5U6jCЉmĻ*"?JT=K'O/|=Vo}l0b}}f?X[?/\JSBe,kP8ETJ==?.p5ފgbU9}ǶdNKk—_$8̸͓ۍ8Di\BԿ-1v{FF]|.^ۅ{vl12׏z7-R7wE?\nh\jN/Kձr_oBw"N QMBZqe-m:ӨSn6j4%!hQ;sv'm4kcM=!8\m[M4{SMliۇ%eֽR&N:{2A8)THLK3Zj[jPBx#BگMf:G1\`edcʮ?|w(-̮vXt,bW2;.ιNHRR#YwTM"<;mk\.foIDjmlJ;vxy7o7i\,KQŊ9d^Mmgc L*.T6tLeIuOH3SJQ3=F/ʿ<9\JM6mN6=<{xkP!F1QR[I$6ُimXu2An2yԒMU q f[IB-'䤯jYm52&JG\zд\~vdg QtHGXw&1Lw+nDEdC1w|YJmvP)HZ>i0BPβә?R:QO["]I_Jʏۍ>QKyu^bycBq4lXF~l [\*N>-J6,Gq(Zr5h]CwYӤU~ʶߑ u*SIv%ZfJ7)! FS*s_\|IŸZ)J ]ܜi4"z[+Z,MOZ))}|Ʀ(RUNIII.S'ˍO~˨rn}M)xxӕ0 eyҵ7YMAB]ӣU:/ѭ*6bcwP͵ "+qēVjŹO|GtY4V j[mLV M -m>",B$ GD1~j6O4|LxnNmqATNR3ε|DŽa[fmn-ڭ+FiK7Pcm;r5 l8r{#-]'nrFh2ruycb;pW=njRqRJ(d mnpckNnʹ+6]tz~E=ʕ l ZZ5jSi3#47.Lcfe`9؏v囜.F\-UZ:*0_<Νu9Lӵm&)_3\^ҹ3"1n1v_|uRʞͫr'iȧN_kH׺8xXrj=\МH)V\ˬ.Xʸ oVRC}ySU9/OBY먌5 ٿwޞ)rw8Ӫi5*5ZΗcGƱ !ZۄlmpjJ -l <R̵/JAպZuq\IdUS 48wXJJtcg4cI~aqߓwŷrm-v)G7yS^7H^-\mŌAq|"m9IBnF㏉9[N+mmy/!KKۉ%n +BdddfFF6FQRN-U5;Sv'm4kcM=Mn)\qιqUd9F%",6MGdT%-+~ f%+y֛^3SrF>6lc(֪vۊN;g._0Sѧ]ETWرkQKzGe9ʨsKA"yC y2\[5 rԭ7Gk5Mzw_4sM3hxЊ'oÍ5jsub )ͪ~tR2H]R͍>̋m6=%(˿(Wrr-܅y5(ܔJ޺YunW̹븹NsqK ]/QR#"ZMDfD|43Qw|._ԡSqTZBg??O Ϥ)/E_U|i}2 9Z?¹0:x'3,whǣ?C y-A~=daJј&M?D1_PS+Oi&;a @;Dž7[ zZC"bv:jjMQk$M RԸ3uA\=wI.AwC"^.{?-\NSiˏ"b}T/}q/ o.1M}R%:-ZniʒL$SgrBW*,Mw'N\ɇ{s\j]VryG'8f`}'N<*/`U숻z CwHq18J+vԕKss4R53/&XTt1bZƟo\=%nO)h$rBi-nKĪ^ ջڜlwkYm[̑+/QrZo%TQ;TLs($2C:s.%+eoNttq۰kK7O0m_t_pZ1SsSM7"mevFZ[w -FJ*T*jФQRg BSu|]g:ɵzjqwmltL.e3sRMچkSmjkmWœިm++¦'tILk*բQ D,PB\lI[9{%Gb R6öۍmX-MaʉA931cs..G4CujQտ[9 }G-xwl)IQz j Ó"rqe&=]꾧֎c)<kӳ+0JrRR3'TnXi^xMF Bު*tIL.[h"2"nKzZe'ZV/RrNYz]8죝n]Ķܩ>^Ժ]u-7^\mZjܣ9+Rmn ߑv?oꋘ?&ƪy^N4o=3-ؔ̿*`}V݁ ƒPu8%$ ݗ]wt;\y\>='OjPIp/nJU8{϶FNMsf"ίNqƹ(+ ݮF2Km |jܴZs%zf*eȫ?]4)I۵nR&FX + [jDh(#哑9q9Eծj8noǕZf\J-l&Z˫}`ӎhyrΉn\űn]9pʌӣ"׮Wt?N4_I_~54#/my1Xr*척aS#DT >q ssΛW;3oUaJSRMDgQnt:Ql,/ ܷfRqiM Ȼ>Cob;A>ڦWقM9X~/!'MW.}Vrߔꔵ!5|iB(0-zF=}okڢE$^wW~nokY߮\6՜̌{i-AF*9)\t9IV6۸5ZUF6R$ŨQIq砳YUZ]eyv >hI櫥N )&l JulwE1GDOuFN2| }馥uC1rޫV+^gdb&W[4<^e4YW,d|htͮsUM)۸8:{3d{AѢ)~ \#J=NdƮꮓ90 |1K$v*?мS ]i$J,C,SG?/_՜pMSƯM|mG1V1$~K>CSvkuj=&) -,yLjuFHK{c駗.SOua;BrSqj-ۍZ#'Jys7[g2z/.u4+XV2VQ.ޕ)$"(%)#Z7suZ%j }BǬݕe)Jvz8zJf:hIN|svO1O#IEcۍjݽ:SdὮvu^@:o^5cs>i/VqmVm]ؔܢn6'vޑ̗J4Wn@OlKbX ;n:hgJ9ŻyǑz8f܌q&Y fN0N;[69 rbׅC2/#kE l&2~èMR.*%g=Ft.%؝e8<.e=Uv{~㻏"EˑnvDѭ͜Lu3u0:U֝$[M5<:oi+V4V9 6nXvx&_ q Qqw3W:uϔ2yb/(ɳ|5zQiJ#r|Hw#.W?4aDŲ\ugWG;Cw鐢K|xg)##=O.dF˟jMUvWĻsr.z]kPc9"]R)mkfOd*uYf١RsB Aîh=k]ʳUrrZsq`d#r$/Ը3o^&lRWȍyuW̦Y4QDUMJ65ƒ[+ygk XK_±k#y:8(TJOSQhJt2.DR}"5[) r)6V6u5k:eXZmv𭤔!푊Q[qQ}ҹLE- 8qIZG|UM4j}Mܕ[Vwm{} Naqµ"ԈM zOpKѰ?IAD3Ir0'/q1itoB5{%wkOBn-ۜduqIzYK60{+DʕܞqIt";r1mG/\/ym[6JƫR \L=S=OT@Ix[TMm{>ݾտ֒ݸӉLYIx>+"JVNzx||5rI?C{oz8۹e\R-^\A2F R+N9 vlT]"ۭ d)t֞i #E2jB@׵=#/N+!ĕhx}I!cM`ąZ*ŻɄҒ߮Y.Z}='/oۙ3IpW̮hT7cTSuz9>B}΄&h!>lӵn~j˅IvU.'v'CSZw8QK3G> ,J59ٷ+HSg䧎hJdzvwv-cvxS5[̊n~ؿ%ַX?O0\6ne 6kn9.ϯ} *h 8_QhLݣ7q +=XBҲ5?[[)+F`=4 }B,sNg==u*Nj9k_GJ)+R~GSPBȒZ:(K]heL=vKPӢwq(NrG^ثϣ?#tC?.ͼ[ۅo؞y#%ǛjVyLSw%T*s92JTM%"YkQО.q)gCͲn8cgi6j1MѾ[{9h^vƘǚםidfi.^RHmg&rׇz:}݃}xT$ضk'5s-狶,\vpbPD،=Okf.c#cdz2FK5T!&)|ntD<+OŹU i-G[EE*FDfeaf2QƤM\UG_{ǹm%\yrGy:.\4wjPGUJޕUV7Do\7Vy_13w;[?c]H\$IJ,*L]3b%L{y.JRKG2sq,B6T}(#nW|km+q5] r㪍bJ@y{byz,b踊3ϻJ,'^xd،)JVw#.Vټc''ÝպWtbRؒJz۠8!o9IۄS95E9ؔ-e9JR{dmnｯ<[~n${~Њ$W?&ՐY_? #a.ߑv?oꋘ?&ơ|y^N4o=3t=~7!/M3>n8W홎2M`Qx+ z qy8%]7_~540ۦ彷]Wq CѡwkďyF5Dum_}~P(5.(X,K9vᯐ?leB9;Jhm#3{CxGE-S{;@Fz˙]=O'!ɿ]' r`:7'2bЖ>Iy,/eTy/V<.H?UYY{\^#ѣr9^7?xoRȆ7EoS_&??zϾM?(~Q-K&>"~aߨ t7Emsϛ+?;fCr)fY+>z$tIkjn_>vnrֳki-˹l= t;'EyC¥|/BLwBJdgjۛ$s S1|ɍV%JI6KvəhzIlBYɒ|0"Sy0F>eo5W)O+X˻u';v)2vVq۳kۮws?UʑBǴYO漪e2MIjPAک\b1)DDؚKm6ZWΨgȕ۶yjڳ 2ضN[C[|r@9Jfo<_eI7q.|cÊV߷:i.:$ȋ)1%%)ADZCEBxJ0MJۥy(bNsKM9k43IwNt.\%N簤I'.j|ƃ2$grBEٌ\}9:v*!n7M(ɽ]7c@XxƱԨ37īf62cTTfFK]9wntQHͮvٱI/f|j=7}\_V5U^+:uljSȃY(XI.ȱmo1甅jڎIZ2>#\*:gY|4k\8ZwSqtyA!+];бޞKծË¥e)#5ap.QK^8VdU{*ѽL\=qmjnB5>{ Ӟ`v±5 ^k&O~Oshɷ,;6nOW>u6{RqS`)S%jp\ipdEBLfTWy$GIYw~䲭J.1vSY5z.V>^+Ǎvc.I[R{QsNR3ӎfhd>y?UJ*}~[e\i5U^͛E]G_FS(Iɿ]i8:4zj~շsW,ˆsy:%O}iur]iF5~3M:Ӟ#N06)4ߧgdawIotiz:1r5YDZLHBSi;NQc44la=Y kQIT*ըl:tq2(է9VO4뒳܂~2rq'nrVZŦ[t7\oլfb/mlpc.I8콚q^1iE~䰳mi[dۧw֤ICfdFeCsg:i| 6擣׋* 96lust^{%99UNRvaMܽo ammi$em4D6DD\nA%$$#}۷/ݕr99JMն[oT޲E"KTaP+HGkŴj5TM5xƱOS-k`ۛkٝWz;{kS}F;~q|~^_|euwnE'pSupUP)V]vE+t =ZRaVdG6= *.ϼnj9:UɷbېmF_tޫgHjVS'śǕًdkkѻ_]Kv?nT>)^e=Ar1'3ԔILyD?:-^in):{7.؂\.:V }#뺾.3r̸*xbFM aȵz 6SQ:ײj[ 8nn iFMw rR"5M5I旘35f^j='j:nNW.ʭocZvZKV^ɚJ.cM1ZI7E'6rg탸5oZ=[m Z`\hbMUR١Ȗĉ):Jin!_7Dй+f̷eKҷvͨBPR(V`y6tw*MRΝcB.ڭTnc;P$8nFvm4(D(R#R-L -2:FP lxZKQc6I("Km%$E, 78uXIFA$RQI$JbInG]c[ֹ:ZM+n^')JmJMJRu{e)7jQDw~%yQl}BZujSSf۩QZ+Dzhd5o%BIc'GZ?}΍:>Ɵivז-%݌J5MqGWTVʦh݇ܟ~Օ_6 n'{3~mϬj'J11OȻn߃r Qr\3y٘+WӍ'WxEs^O3 o~[|7>]]H9݇ZomT@]?5B:Z߂'`V_+/MSKX߆ޠk3?o7y:4R/7þ] iG߬aBRU&?r&/} cQߥGj2?C5Yśe7hU=?+ x龳f-܈czW^7p%-(\D4h{UK&ӡn^m]Fݢ:`δvj俜F+) y[{{ 7 tu>gvrěOj'5 iRg[ͶFjGe n~qT$ci ۚ0oԹc*jL[sVWqj\ݻ&6"WoK:cnWmrv)o>66(F>=W^bf#c zzʞtپy%mՉPël e}J.\Zk4ttt>oEM=q)hJjI=ͥ(%]脼_88ф;͛gWG;Cw~˘$4=uWdĜTثNDkiQL9U*O"4XP`02,Ge-k5$h>ܼ]3vr6!9RQPIVSnM(ۓ{>;/Qͱv{3&-[rc)ܚI$n{Sv3[j00)-D3z}MRzVQпj,T[uVs0\}Sid;r(ݝJ>æʺL&c[jPK0~d(FKÝW\m]GTcF|Iׁ)I3~#oX%vҦEݑؼ5Żv2qAZTE^..M{ʐfȏ2##.R}*KʛZz^ӞN*lPťLf\G6[WVQquV]XAi)5J!,$iJ6o$tPZc;Kjx_n3`qIelV~vLy{fn匋Ѿn%;zV.n'-ұdd2߽1bZksPe3TI9)$ԩIN9Vơ\=2885N\ p)/a柛w9g_lױo8ݷ iixJV& ғRi{N^_oAŮE6Y7I$Nk$|Q)-*4Z)^¸%4Qm [I%.c-OV+C֧R#%ѨCe3i;w$G+_dy| Fzj$DI(=OA gj%v/]8qԯNIS*֩',Q%\44ZZ%D|Ǧʴ6&vֵI$%8(ԬƾS&#Z. }6z?b/|Jl{ץv&mpx4Z$”ڝ4-H%dGKfM:sKSRWeJAn]>s6应-W9'H]'uȫYvgK^\czp|My\鏩w/ËQ.)]\QiS`8uL뚛̸=J"ܻi\å'-)54Ue]:K\퓡vK xwBqrH\*֕TnzC.mT=t-H]SČ~Nu╏NÅ3f|͡G~B+Xm[Q7U{9"~jgK Zoʰ7"qJ,ekSeNGgϳ] ^.6:s}_,%eRg<5⿨z{ZPun#jRІ.6g T.!]xa c#jN$Zpl̋H WZu8WmMRýsĮ?Mco~sx TU҆Q :KDG4n42.<3/'^?6/ܠڒ^yrrÿr2\D}}B]^E~^T cɛ7϶Y[<֞[7d}2%QPqOLEQR\CIsj1?\}%tJ0e~ *sk"*)&ۓEi#{1J8Hrt|'ܝRr8)=ƔN'RVz:cf]F7bZyZUȘ4x8,#JG̒?.W9XnO]KO]%]ƻ O5Γ/3qÓj؍/r̺rƵ 5\&m6h.xoeX[=<3%< lZ"2h\Z[&jW3ejm?k&[]ųj+{N{66leu_+lj]q* 7g*knأYv= q ەdxЬZ|%GUrQ3jLŒqET]1% qkXYūYc[7Ś]QY\jko\</Lc7+'hMSUc6qXyؙ~6#ѯv.0$BQi5YyIhɍiy=KD!n3Vm[V%W-B%swa97ajۗ m+9~]fKq|Ddaˑ0A]_v޺mM5* F-BYHJ5}q>ʉ.6hyDmpD׬'-_v5;5[8K[viJ.3dR:oYHHh9I7:۽fi+wm^ [)odPѱ52CZUJicSw\&_s0uBȍh32džzQflcd^m|7GѹE!fO5]]H9݇ZomT@]?5B:Z߂'`V_+/MSKX߆ޠk3?o7y:4R/7þ] iG߬aBRU&?r&/} cQߥGj2?C5Yśe7hU=?+ x龳f-܈czW^7p%5|Y:SJE\U-(a_cƣUǽXXKiȞNlmۊڭڄR!**ܤMeȽ$|X5(Ź\rJ~ܮ]>'HB0cp XFr_c?f?7<ukSgov¥iG>>䙗i.+t+bOjIܶ . i^:nm}s}(3>NZ$2Qg([".>i.ƾ)B̋M8+"- >eE6DݥJnJˣt׻ 5.˅nJGwZD~!i۶a,Db3ZQ3O#KO5/֍ozuK'GbRi᝘NV_ҝcvם ZoX}F6z 7e5_e:ۓj=AB+iܔERadMBq*ԯ DwI/Gy*mĥiRKg6skY/#SN4e$-yXM YL?^ĸNNӪ{$r1JJRSLO]Aqm>V/s[~i/j+m>z}eI"Qvp]{ZԼ:{vPAG2=T͡@ڐ#u"E*>C;o$~C#_d/HBq^YRٽzIKbOm\~żjFFGdiQ(*/i*#.FF]©m=BmpQQQSP&Ҫ!T&^>:y)$ˑÐFčI Bӡ-t!bM WҦŶ'UZ=}zvn~oT/\ǒ'nr8 AJIӆz<^uߖ4eFC1i+v!3qNyߕni?4JZlmYFXFۼO0B\m[ tʄU3s"Sr(NJ;SKW72L4̏BVdf^Ҹj\]ȱ۪(ӷm?J-KEmWڽ^4<8qu%9pŹW~877ܾeVгS(յe^C]yX͹! םm4FGȋ\y'Z FX7e)|Gjt߹#gb\ŧq_([R8[qU$Z (ʻezV2V!iQ,i$JE˂٩ a(GK'O{vnBvryRd-RK4=qxZJMl_CuuIz @Rt㮽޳!|68\-l[џ84-2Pu" RJ_^OL>G1~XnBŬw6J0*Uvlږ1N G1q9IUm*'oWu][&UyYZbBZRZNfEJf"+2nF~Eû7n1xv.RUM$6 lAxSQJ&n5ܞwlEói"#>4׿Q.nEq7Oko[1wg8ZQwZYiqtm&~">Bo?w͡ni2峋NCEy Ҕ+%ZJ ʩq*fpˤl,~^Mχk1+:ݕ z&Y`KLӪУDr3[*Z :(SL&ݻ۬Vqsyԭs x|iI߽zZrg.:mp%6ԜvgmpIUt;QbS.Է) ǨKSV,*lڌ|5Jt3#NP.=+OZ~/G سIgbꥹJnl_DUM\iM!֔wVZuԺ,yV.Q>f v:݇WiaŸN5Ҕ[M7SsrvǣrMW= \8ZW-jsnڕ.ZnF2qt ً[ٻޘY۷Zm"Jxr&NAfA-݌to9s359݆mZ+N1-qS$D=17 x׵+%_ ve4ir6Z$FDڗnFtOr'7'{9C˨ꤡaYoace{Refnft RR"4%ʌm:Sj3)OdInTO>X'vxV#jܮw9Fog;5.~Y5\~18YQܹvj4+~t7S ﬕs %^۵ڴDZV69R^Y+rj$ԇoJKR5wB9C>Y:l+EǎS{ʲ{T6Wi* ^^9k/y/Cs\g*qڵgn4T8mERr|Ti+iPe;;.i\EBEJ 丬i9ɧM-ԼsGDrZ>r#R>~X9y4b棇9JwV۔%m(b[Tjvl}۩~nDԺ{Zo-YuK1vx.nWuO+jN [ٮ0%"΢CdTJK-RަH"$I(*ve &҉FzB,_Vpqp9m8werv')E;o&QE׵^d9˦j\_,ڵugZȻ̧8k+jK{wmr@3ӭ2 wFkzFVqs1؛.v'I%$[iT]D5Dl2 nk7qUxԫLS+sا3/ΖeZYK<["%-g/kRs:f3;*E ت wJ%)5&+&rw*霣i|sMҴ|;R+fm䡩.!**dӶ-6s6,]zAXMWjmnz%SJߴm2UXw7MQ%<!tKys#P,W>s;3IYwx<+i_\\\U6 u7P|xbn_k&ӓVOe䦒 VUr,-㘘"-LZeOSҠթrEvq8Kf%5%&K"#%vD/.ZYYŏ+p$nZkvއuW9㓱Z G wYIFyf)?ƎUm5ԉ/'k84{KO:rQI}XRuԪ|*lu)3qZ[mSm5R3".Xcَ5c®ࢫI*۳~wRϿQWޝ(EJrri&ۥ^ʶ齲Im|[yb;mnm֩uiܘq>E+Ikx߄3r33-5𹻖09ϖ9[Tz~mr5NsWl$oPusޛ^{Z;);sڹf\3oٹZmԉ/'k84{NO:rQIBø8Bݱ3n֤DiK4u& ofSȒܩx<˘|N0Fչ]qsp"}! QWw@t4ӭ+cO5%]'*{eM߲DRO1y*q8w++e!c߶ܪlZWّM欼 CQ̼빶lX{vib/V/ ai;x6~]+z]MWB>re-:lgk}պ!#9?%܋V-c[z!W?c7YNm/jRr[HOzԻefճ0q15Zp#rkQQ0tU-AmڵP/cȕ?0cZYj;:0ZM=D6g ?'UN+ձ[K ܖB2'xq9{|۫N0ku 7xaj;n\ 2[VznMlWiKbSk))f..)Km)&bGZ=>OR܍W:j'rM'wYz&/鶧{Sʵb"vջq[I-ՌZH._x*BagC'T(Q:$ͳQcMCKy?3g'ߝqnT);qs #ؤZ}OOI:cfnc8W~qy.;^pVl]Hԓ>^H^@7-AA܃nmL(uWܻS߿ Td95Bdh4t6*dDh!EhI[iŨ\L.&Nc ܮf^;$R)\rip9I|ٺ?#R.ZDZ;/]nݻqs\QE9M&Bd ]N mN*D>tgbK>+ˏ.!23]BȔR1ɝ^j'k2ƮqBQq[$di]icV/e`޵B.FIIJqbi>Ӥ|p; 6${)RU>_e}^dzdfzi %ekRVUS?6'hׂ)5.\+qUgzE2C˷ecŏ^֔ibk shesFWJ#~> Wk~ݨ}ڶ>ơǚ)׽ZƉo~B-ڼrvoE:Ʃ3ۣK7+Y`WirS):{>ڛ}:wԨ(J_";6R%[u&ƫdZ_\'np| RJwNeTW,=rrbnkڄ[M3ܴz)3- R.?:okۼ0TU'w{6&w7j1z3ON'fGoO?)S_bQ_¿R(^ԴԴG.EtMڇ&RUiW uQjU> Kiu1d<ѥIQ'RQ1:O/lŗᏩiʂv&Jc{D5 Tt)1.n[n۶X}RjqnOʽ(~[Ns{ސ⛌uO,kgo֢dRNQȄ .'6W!׌P朼tdZjFGE"]K@'i۪N;sI[{SOzk>`rRR+!σj8&TjlvA̷Q?HyjyLHNտJMjܶT۽lG?SnKN%<‘ nq[N0Sq[Ta(&t(|HGO~gvkݻTR4&Z$#ViOY1r$6YF?e4U/Mvxų:zbU^gQQ+NW_'4jfz^c'#`rvrڡ(IJ/J ݦ6 ]-CW |_{v*_q3^DZ}Ic6Uڌ8p7{crZq5ki`)mU6|-Z5^iEz3P=:Cu7DF'k%}<C-޹ֲ̱#\,(f88%X-N(ck0VLR~} G"-8ӏ/ϰKq?(#nrVTmZ;zióM4 m |UT'C^_1X.gXM{%ʤd 4\ovN":"y-,T)fLQgۢr=/CƹǨJVr[a+!rT|%Y\ٱzsS>jͱ.oOc6f$q% ǒGo;n[];ߎjrk{~\VۓNIGn:iqxo |~t5)Rxעri{Vi&NUOl_ѮMfsޕkЄay.0P{7N((BaIP$ K"U6Gl ݙqJRu+qN$ m#*p<|{:>-Ev=86N*MM긭U*uѾ?/^o7;'u,h4݌xښRM:5.(/ \իU.{F^rmF-Jɷ.>Q"[4xT^OZ~mK}T0ݛ^SAo9u?lX(' qj%=X}"^e4wˠ|rܫ 6I\Ķ;Ӻw!'ڍWg{ i U_9Avhۣƾ+:vs/MK[ɭīe{`Zgb}r[i'GE2J7Nez579wRq+Un ]J.cJ4M:h箽Wxxm^ pc\wcN%'My $$| :$Fqɏ¾^қP9J6Wxvu}ݵP>Z'FFdg"-; [¢cmWkÎT8nG%ݣ7*\խCLRYZͤiD&J#'ehbSyXK|y*ӞpS̍R`[pTr/Eg)K+92{_ n3zwz'oŸۤ+sOj J:`T>Cf*lwd\fYOP"R E֢̔L4ɥ :;.b(B02rJ蠟9>V'9M%)IqnhP<%,r'P/vNSwr#w"ݨaqc(|{kd=^0jTMR2ULNz|.<|^PfY22##!,K~E BEJۜ&jRNsHަޛg\r,v؜.jK3)[EJ2ii{KEiHP^&]Gn8x=K}Wx/KI9-ϵwQ%spܾ[^R}S3$qvq8M[ ozKxcqmJ/ӿ{_}7&ݨ\f6ZSyQz& 7ۉ[8~UNn|nkiTB+4RI8'Nc%tn{!]Ȋo.nEmʱn𵵥J A+wy#+ikǒڂ;՛s85'KmE:Ђu""Iģ5p=БbTY-ͽڔ詻ngL2Q}$de# fs^o{DUUsfwӶ;s1T,ǤtޒQ\෼J=.tKU,7čJ5 N$y3kdSMQU~mO[03 $zAڟsF5^뜞"Կ QHmrR"ӳηer+ҔZ]hE-6Jmt'ޒ=O[sQj)6K}?e4v_KfZheޓ=BV[bY}lݒTTЬ{ȫvO_qpRApVŗ 6ju=*BR)g "O1yhb=tqJ gtm\b3RY+JQ^Ō֍\յ\>+uSi{=x ^w;uӘ#ĸzLn*$anok߷CBӷ}5Yqvdž<( "_OWit5:EZj2 B ρ1̊fi[n!HQF82q1牙nqnEpT(2RMoM4ϳOu ':֧_Xjsg jP^(ڙ{2%E͖j^}ZU[Q$'U) <܂%!s"m R'G5M0<+zM6qYm$ڕ$3ǧH]?o2N<8F1̻r_my[Rf59NjpzBnl7*{.QP 3N&^BLJPjAHCK2Q}$#~YMq8 k(MFMU)8MEqTy+Tʞ-ar5yܕOXw!e;q-Jqܶ䓊Y:LC UE{/t>r"lI9)3KJjϤA 6SEE$d߇3KG*En|P\ԭTn6I-ƍKTj<1H_zwGr19wF N8ݝ+a9ɫM6mhePi%mmD! """"""*1bRKrD"vnrM۫mmĽm]ӡiG~e"˩ lhRTMk^MX["Jݱk7_ޕ*DqĒ&flՒ}`W}~SմZ{ĕ~wm*/{{ѹ_-0ط#P]xlڱ~Tn5wi*lڪ (JxioϏbqKYR|!|KN53 OS222$jzww%i}>N)E+rۥ7c$Ofl/LNث\6H9: FY󡈾I)fB֔JI_ ֣^: 9mY{66㒢7Uj]:.-os[R&gMF3˸#໹kmjq^8W"PΦURjʄWa˧T!͋ lW48JB2ko+ /Nw QwQzQ ے%$ޓ7^YL|r7!v%Trܥ &|M8~ybrn[RV gSn{{*#2#ԽᢏӴHak" ӌcwҜw&RJ07ױ>Ļ =^ BɆ)v32.M1=#6%̠tҤnzqMwԣ~s*%-j|_m*.Yx9Sz=)qE4 3pk+,`=kNRڥ=B=nŔNAx)Q$ԩȧ4z3t#Z2lҮYn$S%y- JzGpu|LBV7ZW#;Wwipܷ%(6jFG5#{$D"uۭ~]֫SrD܃fҎӾ+Tu>-ZTQ& N|$沸ii>eRWݳu'[O̻j8JۻEѩ[]vni= ڒ,[_%kC7I3Nv$4ɎЈeٸoUu:[}Do5|zNq=Tre%ɧ6&~DȍF]ƞG5q m]/w/ \ʲr8=oʔe9U(W"|S]uZd#?Se[W"ֿh][-7Nu:T=)R}.;ml*5Dlf $fF(̏T hiIUU4Szɕ t(%_|2 ~6eM;TƗK[f&]LK^CE2[ȏBOd;Mi|cx,^6;sیGpQ\NuJIFTJ~đArh* B"$H쉩eXPRj?sl"ԥ)su]xpԴY%VESH"ЋJǰ K&5^Ukzׄ8kEgS2h&Se\ Yl]WҶp-ZUvi7QS:4byqOo+[̺腋[6-_Fo.6[7$p&^ _GZԸߍkc.qqoI[9m߸YxOZЦ1uoiSH)P9Uʄjcq= S>֙NeR><;+ڌk%_qT].srNO?s[=vH[]RZHRMtᩗVؾ:/~u)ԍdg%=edVrISb{6vSu=(ܥ)mTv/J}̇8 S3ad:^hBSf؉OɔLhI_1d8,L><_A0y3rXq"'(۱;mFNII.v5_(^q~X>y{3צ I*Vܛv/jW' T'NR'j%ꔩ:mJ3SB}΋!-H-RJBТQoedi9tjENenPpke.%4]#{:>mkEɱdYWl\\\'nRM4&U>?Ќˉk÷!𴪛]]5}UqG~ݏI"O~s6(Ļ)qO~h}uԕd}Q~G,oE!&G&/]_H-O=o{k\̭bkv.Ô܈+;arZx)m?M\3lU$mk-CFXjTv6u' g:Vn_*qk:VC A%'4JV%EY)#BғO4<e׿jQQ]yUr4=wm[K1r׵%Iũ-O}|kC;/VcݩWZ)EHdžTru]8hgĵ-;=>U_ InvTm_jBM+QiF"9*{DI/iuo(=TzϖmPQl_v4z>T*ȴ>YF;ε\t]EH4ꌇ[VrLzef 2T^V>g2~kg5~Nק;{~Z~W}&ŒBӿS2$J?~(Yœ"˲ߩ\O]: J׉ښT{mmIѩn3˧)4LdFZ/zUG>U> n 5& ϴ-KJi2o]uKljvK3$bԔҚV旧iY5.ίfi96v7!v))FJM4{jG~Jt/lUE%pTAFe4qQk\ve۽/u/Im+W')v{\-E|Pms7߮DZRr۞/mu*1ՙaB܆ -xg3#6ۥtRogʌU)׎]ZҞNnŞr}F1Nnޞ;cZ{N}ۿMiuxʉ*3qi'9KHQ$WJxXyرŔe~[v5~/jN9Q4o6rJv FrdxM*iRjMzUinHdн7ᾞS=S'7 } ̽zt7K|_g J=Lq+/Bw_\ۧx\HJUPzQ<hqF[V0x==CsU7q|^ {)Iq38$_A(VgcKu06Ƅ"%i~_ˉk QCܣB8Ku/񋇵u([w}$F|8TՠI.E !;RJ^}MɒD_q2];Ɖ{5}*n7nEInO{Mwv}&q+v [V}Ĝ@%>#dXQ$f;iep.GquixVt x6bj͵mlKقQ[T]zs/&yەnM'W}!Fp_d^Tu N{ɻ'l{խ2.sTu{W^H&;1s)Pӛ6>$mě;Łnj= fLT)>׸+qReɴ[UR\L*P/!$Ӊ3Q 'K=m~6XqW3^W+ųO_[F$rR*u"T%@O +%# ]˽!aܽz{ͷvQh쩎]hGތ5ɇ*DzJDRNLi 4:{~2FmXY-zzĽ^f=]uū{/+&c:Ma{ĝDp2m܍kHș/(--m_vݮK(V{R}.k&yƴ7i^4@3f sK3^Ř˸B=]?gt5KbZB<e;kQLpxuWC}n 5ҴepB##~q= `x]KWF {GfŲ}?G.I9pjWkU]>={7q{kO/^I3==f1ɏ%nnʫ/Zu_yXN<57ۍ'vy/"8넭M2eԷ&Y,в33%IkjMr7xf nmQkX4踼>a-GcIeތw&U=-:qnW)z¥j :WqSZvԒ#j"KrIU)%qrmRoDGQ~SYRsu*V)  ,/x)MFD6O#]z 96[Ui(JRfw'y$GeUީkdMF-ݻ98F2d[o{Rn0n-xsV6Dh|Eb2E:KCOӪv4SJCr"J!!m,hRLD| ZYFm/X~ΧfrN&4Ƒ=Z9Mh.Mܵw/BdrܥniŪ8ɧ|y%œ[M=_tj?F!z5\evM:\ ~F-sg钬OWq“iiȍ<Gi%%n2rqͻllƑ)okw7}\Uk-:&fj솘XerV9yZuʼşdFC=rmo%~ZN78X(N)_7.Εn1MpJ}62jjJdI";R5&iLԸc:jmqiQj$ujp\{;v5B񥍪Xn Ą4qOERjzN(Ga٠䌡)p*v(J7#ZۻZ8O W uONb+^Qipv9GvֽƼϯrYƖKGJQDNPhRJjᡧC"21"9ѓS1;R_O7/WGz)8fE%F2ukmvSov/iZ&/]~KmI[:^~ͤ\kMi稜\ywJt3W7 8Ʒ~ݥeFgѼw"8VVSج\뻆}ݭ/J6Q)d|)zU3>k\L=;ow֯gN3pKѫ|wmkZ$z^2R:E)f>ς нd|#׆?\ǔpV{;\$ƵE%-ͪm0S6[n< kE[}mvE4DDZ^$OZ0*$~XUv҅B@^?]so#%ojw;Y#SxxueBگy v^i-)s)zV jC{7Gt.w3v,ygg8s]aE_,*E tY5k٨h=o"m泏:\6w噓aiL׎n^c\75AGkЯ0Lf46َ`egZ˓p/k;̛]kq!ݸzpԭG"}R9Ve>ˏHUjJ-&7nrnwG*Xv\˱/vN}O)ʼn&CV͍f̵]r\PMB-6Du-#RͰtRN^)mT _}nSȕC*_xBuTkJW[`ɩ`ejvsngP ڻ.-WUtܑqԹQj)t;vN&RNũT+8%IXӃ5fK՛-d9 ]CƑm|nZ-6=Hz,*aEm W3VzRšdY~Xf׀Xx"]s;)5u*ُHB BRGS6bݶؿ 9j[1*jױga7oX CUI%0v#~\-O-Ꙛuɷ쏪&5mY٦M`LJ2qK~HZbr =N'YobI. (^ ׾{_ ?OJ`S`3BN[}5w6:ǵ/iSlt=4F*d&T4y/#. ɵim5Uֲf 眕6Y7 fơ=3dϕq뚩$qTM-%r!$@A? ޾V0c~{[{;򥧅a~ڵ»&ڄv1ek=wb MLkNAԬw-x>~/r=e73VeVN)K%Sښe"+3uXuچrn ֺVzscJ峻m}vb㶓n\YbIUBT%*,0nov=;z꣓S/nSXSpl##k9mXGrZv^Gde!ŷRԠzQyjC]`gToPov{j~KRBMY}i[߶9KL2ԉO0K#m>wB[ٍ+n[[b٦DX ݲpo] [\m5qdT()mo4Oy9Ie b][wղmM~vmi۱~t \}$яimRk(L c Cvk7r9_r1 ;zv|F@KyZ[&jEji/"6$69ml#e]9s\{ScL}Ȣؿ0q/nZ*t,CLoD߉Njǚy=Pgmu6^]l-["çUʖMlʍp-"qmU>۷uFOJ%Ǔkx 'g=睋k[3u,{³WɘݪF]ՍeFX"Oy\,cچ=w/gn Ļ]#2? vqy-gXnR.^}ݺFs{ŝG]}e|#0mjx"ƬWكm?rgU^xVB":Dt>@LRbun~ݭ,w+v⪕;\U(RYa61>#Jm˞Μ9g9XKaG='u8gf}'qy#ɉw J]We.ʲ-<+&q%s?2dњztҼn`cΤmmqMdz O[-ߩӲ&;[tmܝVnr">{x<8U+p:Ig]zjGkt,uzf}dؠoJaکqEq -(:d<պ=eKy[˗^%ZXkX[C2߱\ITTLGzANM￵i]K>UsOGDDD.ZF6* ҃V Zhz{'xp^`wo8r0h ZmJ5"jb[l=yUu7-;7IT%:jFjߖm0tzU'K)څNۧYJ)4IQ}^KWm7kSP>q;ނ#)'n7&׊r?óM{IwR\j2Qn[v pe#/tAF\ϵ225q֒om6z})6҅*oqDsMf CNIN=T S2t,_ѧ}kveMF0J\Rnnݙܹy[rUc-j{yGtkQ%s]5qB.Nw.JN1LvR Ui5J ZESQԙr):MJ+g}χ!2;q([jAud][ljVK3$ײSJI=/|&tl'*n۽f.frܥ jQO8>&Z];.|7T/C}$ڋUmP2Reҭ8hFF\L 3~e v\۫]ݝNmrnB%*]Z«hKc=BTLG :V74$=Ǘy+EX'4tn(I:Ѝ;Df8c,k1%dJ6.j6ź{N~l6&*fœI7 WAlGOu-ҢH,,(ǔe뿋쩨kM܍ZſgRvQ' 9)?n|er˭|I|-fGK.rΛp8XV1%K6mvG+tc+qE&ǸC_Nm:l=_/m5^[dߌڇ.c<%:)tQ$Ow~-aY;UJ>=F)2[nk؆?훐M=l6[4(O.]2#-H^n#->&mp5~Fӛ+|| S,xag%qkEUzUgæBhߕP(7]kFnq?֖CpruZ6*rEڊtS|*tI*E}7R<,nUU֫^I7Q*mSly%rdȓd8hE<9oHhMfNSRj[i7D[Rj݊+kდq{"$$H?p\̅S?㭻;t~R߁)^/>Qj`yt[w ԛ;²~+ߔ_ YW~|o]?x^ᯛ `ʼn;g)T@vWn]>&4lp+$D̢1l|ȨF%-}.9[}w~ ԠLM9hСablfe&QoW!s?wjLK?s7yO>(=C~_nyǜu?v3vyo oI@qV-jeES^[9WoSܝh"l2C1a͔CiJ@3:Pճw=/7ovuk+\V;lDgն<[A+rX~d;m!_s8ݖ׷;;.0llUC+?i#_crʙ1~C.\–q ul8Hܶ2m`ܻM3Tov|Bs rɵ"oLS- DКw=Tv@f'6|YlD͓Y%׵-#Ѯo%:&!3o%\J<02;K87>^vgƓ# ;ݝmz^Y6=PS39U%~ &f# }o!muH;ʲŇ˷yvP+&.7e[3'vR4Yj̗IZ`e˽3o[WU{ m[sUbۋZǾۆl6~9'V*.\S2<Sd*zY[aŶ`]C$n.v^Ʌ dng>ەZ,Mmϑ :n6nϦezWqUJ4! ۇ4R! =>>Fn|Q[{pRO17ƕ~._I''00k=b՛o}Osðc2'o\3}ݭQ^2 . R1yKȣtAݿ-uܾw!`?1Whn|gzUo[ECWwjUIן)^h#1ɭ!/Z np;o;ΗŻkXs."6E`Z1 עӐ9Kl8qd q} 2Stt;#j>;խabONŗ=fwP1j)l6J̶|gV2`y/0E˛6+ԫ1? 6}KW c\KoKͨ2ۅFw–s*TԞLיuDx .kCzWXhy۶gLu|%TnupǺl-S* PRaLnT+c+*xl.v!.U=|; !_L̎뱚U=4hm:ٯ"y)$:>%(n}X'p[ȴ ^˒4kƓmzDx \ 'NqamP7nyN݅=j7%McSڵj%STy qXymvCg{w/w=wSW5r̹u erծˊsOm=DhEҚRb#n)QOxtվQwe]I}wCa'"[ۂ-z}2UuKP$㜉ԧ:mc<Ý>RoL?wu|%ҷ&K y_!y9 ??:tq3(UU-lkS'ɸ@jdzQˬR] EVPW1DJq2n:,c|ǻ̑;y{X,ۂ.u.b˕u.tKBjQ"[S園S`ٮdNبeJ&9Ơ ~0a(Vm٘L+Jr*vڑE( x0+tp˕ n';wm-ޜMOxX>{#2%jgb2M[`K*\5@8l'e=0u+w ֘鳾{y܀:R*Ya]"Ӧ%ktynlۣ65,3gU}{GYrb;ge'TKwǘ.,rpܚV]Tr,!dp /ԺU,xՉ>s׽~W5oTh yx?xrrx?)?ilbT׬,z$Ԏ.UH٠\U1pU:]JwSrGZq8àd驐,N67QYBӢD㏙W!Q25ϸo9ms-7-%3CihO.J鯽-;MZM8ku-7k9S$8]q2E(}bۏI[DKOK}3KUB^u %Y,u.-&f#]'܆o$x`Yu,dzwM;#oKxn;\[d7}Rb+*Y䛂ZuBӱl{j0O̓}LhK;[aֶaGL{Cb#S.T[>߃F]NK"u^LUʐ_ykW?!GRj29͖qa'0[npcDvV)qz9R)PۨM^aJx W] r>];eN3vxdmĘ(5W2K1䪖weF{mE/QP6\u54x5[hۮ-Nk”i[lUgL]J}5 S:EhiUrgHl!ŒJ$pe=q^b͵Q' ?6|R\,JA ڵ"TDꈭ:ymg`B5t%M] <N_zv2_Ortٵ/i/ReӮ*7[qүqEG* m"[I:6e^p"I$jԴęh!m)]GZkcjS!{e^z}+Cѥ9;R|/ֱeiUԏCNu2Zhcٗg$ݭwvr P8*7/Lk~I'Km1+MW%Bk|oOm>-#qj*|Dbѱkn|n{v#jĮqNpMIUm(7Liz;{ҜݞڝVƚVϬ+sO!OstGvxӉ']uӎ4g_ 1^-8ۦ k!)Ύ5O;YSB#2Zzχ;<.ֵOtge~.(RC#wFZeGZٸ6FFJ4e2ˇpJT$[wgV)q6muDGJ56q\I!̗ y/I~RtJ9kJ]Iy*'FN0s.[l!fw'y(7$œ WƫgyΙdMEU JQJv̋vmrۖ.jWR_M֨djYgSj0^\y'EoECjm$ IƩK>Z28J2TiJ2N#}.s cArl嫶nB.FIJ.)۔\ZiM>/hLĸ=C1s[?YMqp|94- 鮝𦔽/k^#NT(Y LS$6˩}{;5 )B۷W$qpN)qqoot}ZDVә;7TiK|6f3h$dԄ}fqݡ>Nb򗉉+ͶO]>ߡ_VtYf79ڰիF sq~prս|QM)g%l0ocJȨHz V;Bb/kLAcfPJ,ԭ{ƍgpjNR6VSI*$!yV足jᇑ.](EܣqM\qJ2eZT).<9UB/(B0j)mtKEj#׿fDI-=rZړj|'Nڤ]k*i$5qt"ݙPM6E4ke^Z8ۏhz$Q(R Ay2zfRñnpnkbkI:=j &ΝșW?׵d{+ύM'??XqeeĽ.[o=UxFS=ӷdZwenՄ]_X=ĭVa* pKs0ބۍfJ3 gz̚i|wnxtjc¼5${(1fXQ65ȼb̶Zkn>%FQMJXӡ{TZEVNᖣimT/37cNJUPnP҂ZOE~"-Rc4^b- FEͧtf5[)S!OZIښݲ͑;tvܡ+N)AR=hCNn;wL16-:特7M$=Tҕ-.R[HٷnXk sn[ҞD-0WS9p9:-Ϸ-jѬNu{ҹfv)[Ľvwfg(ٷfe+0mYj8Q1\ݧg]Eǎvڿc!4#j5̋C2"}BRriFp7=ô\TZ:\BLfj#I22װ<;صZl j 6:l"6]۸ K'6RTѯ^ئOԓV\?$x7s#r:Oh{ց=MmuHԷd{pN /܅:UE#Yy+(SgQ(Щ)RHzw>^Ѿݻ>mK&^ '$Jۻ&w%F|xfz%˳ L~3N?Cy9 v w/{ƿ kz3x> sXv}vP"@WyC z`'톽Dw%-tt yVY\wmuPYQA0iG-2JP,6/gˢ]u.-n!Zw.N7Q]Df}Q0({a\@=i_X7gFǘ8^⻲}G MZ1)WEfO12G+=-B@z\`||w6ċj߬m}UwRox֢I &c~XGP6Qndpvܻul'V7^FJt^{b^B(L~sѣ6@߿^xqU!ڙ5|Vpvef-uӥ^3  FSDɯKD%0r}FF穛r7 +o"V8tv̖NQU!5uFd"bCr^bJ=֤fM#ʳԷP0O-9xRBm\=`r-:;~3Tl(nXtXi%2Vٛ#vwqƴ`L@"H‹qW.j,JM5B[)WܺUeZFqc'V˷1W7V̾-MHФwn8N;HPSdݷC7&2j.W\τGŎ'Vb]c.x+Rx1%C2T{myg[qU|+m:M:շ8҉yWd)ՋWS%%:iqlʹmGwݹ WnNŤѩ5(9hTٵDdGUi-)vSs2 2{OnT$Xck n:¶(lASLeȔBjμPpTb2~N2~%^k[ܗ[Jzs0ӓHBKq[}JَA-$dFQgjxxFv4r/x*Rm% `4J(&iv7SkԲmSH1YWmx 8n.k']:Z˭_W >ڃXЩ. jTq%Aā[E}amc]D:rmHRiu:uӚӢ\p(5-q%e)(۬ҖȽIf<߽pr&ݫVfY91q2ĭEQgYbTGQ&,yL+N$[q*RVۉQ=FuTܻ>f>f㋳8N6$܌n)9&»iˤsX,݅܍ȩv+sRTpO}d?Wn/Inpȸ%O]StQO|v5\}7Zwb.AIVK^:wb{[uݯcytO߶S<{8KSRׁH̏N7ۚ[xkwYy_'ZӵF+>쌛ZUĦreE9F[24De{}@:ExWs-\ǻ7K-\JNvEk%:s˙#κ].oͳ;լ7wB6nwu:$L; DkI#Wz.:Xp(˅v$Sq,wn\qIN-e<5Oe+vuYTpcojUI_ާP8 O 7&VL8z$_B-H-[uh]T{|8=qVRN-:Ij:7PUtXϷmy鉿:RIM~33ӸS2#׳GdŲ5+/Bx{(WzȨ5Y㞎#|˖+ ط.|e<o/rߔX>7s}VE.OVti׽ .5nNJO"95{#q}Ay9do]R"M6z\tnNS-D!@3N_jicWsy*5uٮRcWv/.,j}=S)j5C^> Ie =gu9ӛqjtz]۪TMoߧI!Ǧ¶m:,"[L!{qAv-o 3{"KʼnrIkfٶj2ƙ؄S`7` k6jzޞ?e5G&6uʷ2%ԒRKE*G\Npom F/V |C0.q_eenƣ<5Oh'67ɪn[SĽ{ڔjǘzs;~׌(ۂ`ܢ1ƣ` _l9Va6%UQWh~P~\F^ZHR@:ۧCJ{ôGeBh;~ۧnU J\O+n2 RҠ)ng}Kh{5+S×ܛ.1ZjG)iRȤIN 4%{oΜ/eO[Nffd ĹK?nnԼMqX'܌nZvq<ķbFnͪaQ`5 s,M_լ?-@_{w{ӺձJ}GF[%v\5[ŒGkOw/ΜM9rjË%2+rd~+󲕛C9U۳r[aJǭm|˒LAʨSCq[XMۺoubfp:t+ΤĻo ][ zt-*67kvS7D·MMCQXm;)܎n_h%]4ܙnRk!]ڵsDUF"`R, &#R_*[z*ZqFXɻ]7|۵w+'pFDەs=r./ᐚm3Hשy yD"jHCr':sA65نѮ^o1V/ f;nFr3VM)e*- s D'H݅fӧ\*޷[k<7u<-]֍Q8R h|p=WlW3s%Q %3l}@U-K6f-NϿu|ڴmWN׮[׸F*mW\%r! C78:޳vBG7ŵ.JթԚ2x)ST!řn~9 W:Wpܢ件{xf8ٳwKE ҰWxVB\qBZ 2wMb[lGSnyԚ~z9ZmያvoN2Afnݽjf>)j3 !;gOYʹK" Wftڎ+׭b*2ϻK>ۢӱeyԪXISUm[z+ugX%0lϏnvg!;t{BqPj>PyvR7Cj]O%+ݲ :qiMj6W}3vC/R=4Som]ŗ=ю, TF6U_-\6MyskwMr&Q\wjKܩyMϣUj0*}RZܷSdY3>Zjqj6TgzpA/M`/Cmл,޻feE[/+uk^Vs1W$G(JsW2ٰu*߻q*Y޵.Wi:ur5T),=0uRmho.twܖiYwrWHntvEj8qhf`Ͻpf(R&>Ki%I7$QӖm-2 ~yߗQ-앑/ x[k8nw.c㩵k}]FkbJl:{.(˩n0Hqvαp7 귎.Gupx[N`Yq'+ruU7[ү+>!xrȫoSo]OC# d^Q]\>!ƛGw^Mx"-+%vdX-:M2UR%d>%l ioSu6lsj7D P>XxHz Ukà(n^Q V>5cVtWj SEiJdznyej[lE' 3kuٌNn4JW)gB {4 j6&]' m-(ZMEz8cz>WZ6#7+[,MR-Z!4ܓtCyE|umj1ƽvƷV\;%>Q :#Le(iVz5 4ũۤUWxX ^(ҔsլB2w-V ^R+; ˂M\z+Uwr+RWY⺧~ Q*JcYSNSλUd8in=v K낫k\IRרSUaCFmϿ5̗P|u ZTԕ}>oYѲ1sfP+sQkX8Gb~6r,s>^\,mGL+7[n-E\.Fqḕcl*Jmjb5 ,m]c}NXfeVlǸJ5eˡ$4%g~N p4Y*WwW٧<8v#;qԩTut,m"#Y D\5V`\\Lȋ];LȇiS6ϝZ l>LruR\v=ǘϔDg=ԈdFZ+M{=|,[;0>RiSi4,S5}yxw&(E7&fݙ4UՕ! ~'Id)]ǽu2K-fޭ \08Vڅ쓬=Vy^^ IhyKR-B#Ըr=]mܻӾ'*Umkoy rTqT_i,/8Q^<ݤ|4ԻO(܄"'5N~#m.(Ҿ2i6Uev&I*<}҄$eNtÛzyWJubW^iBW.܅Wڮg]irO6Ve90sgv.+sV޿aޔ[p?3q*FutUo*eL\KM'EG*ZcAFfG5J 5jj=MJ3OK:k˝'NMB7m3uFҕ\-Ywg%PRqMIyZGY9|μvn߻5cWݷa^+X֥vnݘ\v7m>Fgzv"-;Ew֝}1|RjN𿊀7g#֟*GQQ|#/bo]p$>_Un9гUbn9׃ErQBU-^vDmVh'<R[fdHT]*~}3j;nvjc7s-rӳ Y8[n[1pJx kX[Jk9Mn!_Nю6x:iZ˦U |߉^Ԛ݃hYxk &U^bwKk.[jE+P(˞=9j@snCv7%c_7=xǁ<l {t'酚+1F‹l׭:ݻILruǶkL-L(K0L1&>wXB(pm;1fpnlp֓%Skidkt(U +xulo'/ڕeN r=^pZZ:Pnj8Hf"48ijY[ N[yZٻ+=  ø:3 ?^ܷ^Sr#YK[UF?CuhC b]GM')mڏsNrܗI]ljq6VB. W,UK"YX5{c >Iqā> T:n!,5l2VzCl|+I[*SrjnS6٨y+x,@>П.g+!rn9>N|W>OZT_ut Y""v7|sfި;Pclm EùN,{'fNT%U&LfH8~1v>Il}统u6P˗c(WV~H^bMU.o*oOF0N:_:6Smr_.b+|ݶYY غF,mwjv>f*>QM뭱Sd:`N{l/⎱;n-z~"Gze퇎J5S KG9!Gn;N1 ݎ h6m|S?ɂ5'WOÞ 7|7^ao @mxGmi^jϽ>01Mf0լD3-2T. VXR"ɥV Kl J O7|u?bvа;6.eߓ|[1bmRr,eRz`z 6܎-ͨku͹Fː dPhYgZUj}nvX;z=gVեTv_J }\1n7w2J?ޘγc\E 1Aޑzq;\r]]\Y&[nsNei\uURje*Qk2CSl*xJz-xٶlm+|UjUؓ`Ladqiĩ!Gd\W~fz;Tn*PdRM&T4`չSWq5k훶(N"Ӎ% V]֦wb.nUO!u*J&Oӕ2e|Z=eV쫚΅g#+/RW:طnbi*Wyo)p{:ETKؚR(RY+r웓r(IF) VmȵNB:h Q1ғ|u8E]{,'$-TR[j49l*3"I鯴zhd>Q+\BkNF=.$ZR4Nwհ(IpNi.(Gi33#33e$FXK*NdWrud[r{xnk$v2ıh+J1TQ[#JQl[tRO]LHKٮ NӍnF񨔤֞Em'MILB"ԋ%dBŋ+p̿_17jzT~4pc Vo\ƹb9Rq-'1j;8ܗ)hE%DZKS<璸Bu*%*Yw5ڻ9ۣ^z4U; Ñk\U(o~G?VUĎ:?P?_F_Kߤ~ᓾI |pr.Ok\SklRhҪz{­P .}SktZ7UQ4ڌIM8̈eaӊJZ%FFZu,KZvln廐SNFIVtuNi?CM5]+Ph,{jN JSR$IS^tSUVrORYu.9WyP6 [Kiu m!X|]Y79ӄ)\ģ)pbڳr%*&ꑶ_-H*dzk)1 V3')UAϹٶWRxe'պn۫h7AR9 EAJeGLms!%D| A 5]/Q3eb̄vnVn%za\m kZnv([emqrIҕij|""><hjJשvvǕ|Pޟs}V~2&Z?+2N&Z4w@)4iSڪ_>/JN9Hiۏuf8'It[ȲR.hZ$ȋ_Y ~U<UUO*6b)Ovzڜj\R̋.$FsQuҊj^נ䈈y<zZIuP[}Qm=C?zN(Exqu/kn S-FzKZzOסӽjJ\)F3b!r5ٝ|;6 o=-3*λ]αb\abqRi-w޵⦪~b8Kpo)Z=>)ғ"5/GTZLE-輵f7ݘ۹~+&+w/7GFI:l33fg.N~۲\2|*cnermnnM+Fq"ѪIz%j =YW8@~gc/~?N'?)«qȸs➟n=k" X“m֮VreMh2[uݖ] *FܖN)MȐ`f0 g,C9̑o;ddudJ=In13:ݒvvdMUEJLp^,6t-@͐9'{7m{-3,>hnF;ѰM)->>+Ěz!R* :`e--m7nB\u{b U>[8֪]6^ߤLʦ\DFNo$$dͶlgno8OrsQ\l̯hRo8tuNo+ CTxu!2[>ctFpeޓƻֶR"3QrQuOѳgwQr;S~)6HhZw/GgVTmUf_yt7%$];zLWF̰xy2Ʉu!MCmš_0[W6jf#a-KLi+3Q7c^qg%s<1aYIQeZf+}>;S6L0]Yu_h9߻<ƅpmiM$AVvŚ,*#t2.8Y)-Zhshü97/#Oro"u^/uFgWɺ,p:6a,^x%$Yve^3PƗMnTP&yS}OJ '덫MH^:rXԴJۋ/rI;S*,+yz1hv)Qw^ڍJ2oL׊q(\fDj:^T%vOadɂnS}ZO)N*λdaȜkG_PIEO}нa(^iQX᯦-7^)%g'SJx(.S9zVɴZ{E ))ۅi/s7 VIV-|sj0*UBTHIqRf>FP$KqN0 R̻8j\GcC}IUz\i 6F)Q{Gҧ3qSzKj-Az VЛS-zy:8*mNk|D鿓ND2u+0Yŝ7kqm·?8Ib]u>˗^_>(]vӋzv+ݩ){vZrJ2RQ몋C$z [,pp,8mڊbR]Il .f~d/ݓs㓓mͶ{mgjQwn=Oic9ܚm4Q/6ݨ[TƧ?nԶoytf{@AzT{e{[O'ZRZt~AGD?s3􌿂ՉIw'|~U\ w~di:Kޱ)U/sU%njѩ&GSP^ǝd)..!^U` 1wX[aԇSxoFV6_扐)T 2Mfd=ۖͭiZ7KK Bi9%7@<3<ճԻU,},a}FRqɛr i@ONJvK KLN M, ʖv0n-]DwlI-X6ܶ$Jʴh5O+mOI+Ra瞠\ MG7BفjYo1#͖0V`Ѱ2M?c8>-Crt*JkIGS:e#hPKx[鱼>{5m;wcն&>j-M֥^َ) 6yȜl_w{-ō̱r> U=]iw3)r*]:K]6BdCTZ|>gf}LW}[$'Y5 &c -j.z6R 67MԷFMnÌwI7w5E}o޽+K ֵy4܌ȥW"COyR[q5Ӱ͙f[v"_#q{MV6܍3"u9BK(41ӯqˇc${ߝCi6I(OmθzҜ5k^:>Jzw.>qV8{vU[ڶEm|DžBz].KHjI]x;Mɗ{m,qZXr忇2u^RO2Z}ZێS[2Jen!*NDcrBUً4<ǼMҲs1Zw57c3&ĖڻzmP*FuJG1-dN:|OU}ҵgi2t~F^^Z.VxjvŧnNNh<:]^~NN+ge^g.SԔGFe߯'[vn'(ScJ]kܗ7eJOlRrfziݮq̋S"\*U<*W]k$FջV}? 7g#֟*GQQ|#/bo]p$>_Un9;l S VvQU%OLU{οmU6bZ1MTx%!֙Q7, J=!3 ;Q,ڌ;6ͱ݅q^&ߔ·n #WbwӖX.HtG)N&d̵zpI,n cu ޖUj+VXUp[w]N o.J6Z8Ts&utxln;~HPHS/xw`G\ʡ¿rj Z^vt"[L:SD\h0sUwR,}[x^X,R2Vn< ]2YDr[SRKs8tXb̷G?Ps Tv 3be,zVz D[/I.KOEQrm'$7|[J>r S`5յwT#\w1FTz\Ԛ &"ׅhSHrD\'r]~/>p;:Piuu:"9ő=tTaS7V2rӷk7mb[^WmPp*[y.Þ6f]cizJCgRR@UVl큝.WJP1N{/\whZ ػϧӱE7|E֫Sί.x-Y&pi%v''-x6r'Ws*6=DwwUu]=C?MK [yrtܒG$!WGqJ*%SAz ED[^)/tė/g=#Omd.|^n/sl׉g DZqemqowݮRzUܜ=ڽ-o/Iۖ;qVʘgPp|mm;6zGl9.8pwWgsJ2qPbe}}UpNjٯ}7TMQKrؽtEx%v w߾8%|j;~|}pK]ơ/ w߾8%|j;~|}pK]ơ/ w&~e_H 8PL7:%ʭ5Kw&U2vwR_+rm'}C7#rWoO&HoG?M$UR7{FU]u ;# !Wk`|W>׹潇9Vn)6)*ҹ{%qV4q>W1vi#T"Qk&GwxcJBJ- Ϸ^ˁxkU}ԣ/3.;]J=<*)cS)ROK9H=,r zX @)cS)Da^ԽQ gxJI=w֣gf*TRj

#E-mail: hpshin@dongyang.ac.kr, TEL: +82-2-2610-1816
• Received: September 9, 2024   • Revised: October 29, 2024   • Accepted: November 11, 2024

Copyright © The Korean Society for Precision Engineering

This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

  • 34 Views
  • 5 Download
prev next

Full Article

Download PDF Download PDF
  • A circular flexure hinge is a core element for force transmission and relative motion of precision stages used in semiconductor processes. When designing a circular flexure hinge, calculation formulas for axial and rotational compliance are essential. However, in the case of axial compliance, results of the existing calculation formulas have significant differences from reliable finite element analysis results. In this study, calculation formulas for axial compliance of the circular flexure hinges were derived based on stress distribution phenomenon. Comparison with finite element analysis results confirmed that the newly developed calculation formulas were more accurate than existing ones. It is anticipated that these enhanced formulas will lead to more precise designs, ultimately reducing both time and costs in research and industry.
  • KEYWORDS: Precision stage, Flexure hinge, Phenomenon-based, Axial compliance, Finite element analysis
  • KEYWORDS: 정밀 스테이지, 플렉셔 힌지, 현상-기반, 축방향 연성, 유한요소해석
Precision stages widely used in semiconductor etching processes use flexure hinges as connecting elements for rotational motion [1-3]. Conventional hinges, which are joints for relative rotational motion, have backlash and use lubricants, so they are not suitable for semiconductor processes where precision and contaminants significantly affect yields. However, the flexure hinge is free from these problems because it is made of a monolithic metal structure and is therefore widely adopted in semiconductor processes. Many studies have been conducted for a long time to calculate the axial compliance and bending compliance values of flexure hinges. Since most flexure hinges, including circular and elliptical notch flexure hinges, can be viewed as beams whose cross-sectional shape changes continuously in the axial direction, most previous studies have used the Timoshenko-Ehrenfest beam theory for analysis [4,5].
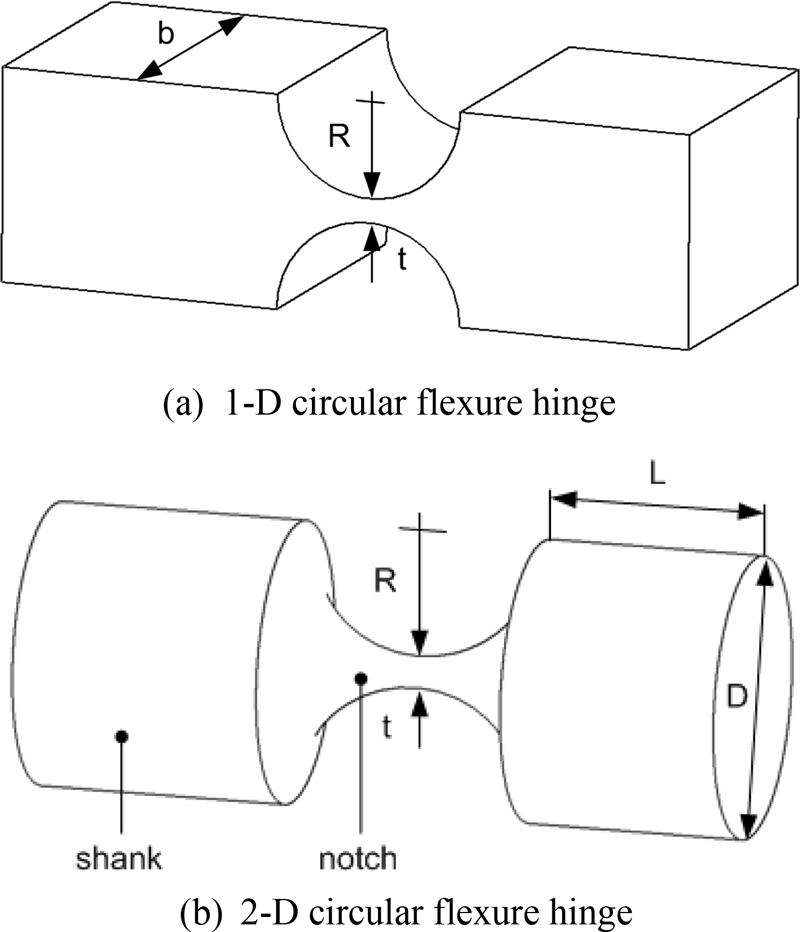
There have been studies by Paros and Weisbord [6], Wu and Zhou [7], and Lobontiu [8] to calculate the compliance of 1-D circular flexure hinges (see Fig. 1). Although the forms of the compliance calculation equations developed in these studies are different, we found that they are the same equations when the terms in their equations were expanded and compared in this study. This is consistent with the diagnosis in the paper by Yong et al. [9] that the calculation results of these equations are the same, and the reason is that these equations are derived based on the same Timoshenko-Ehrenfest beam theory. It is noteworthy that the Paros-Weisbord simplified formulas for the rotational compliance are more similar to the finite element analysis (FEA) results than the analytically derived full equations. In addition, Smith et al. [10], Tseytlin [11], and Schotborgh et al. [12] presented rotational compliance formulas for 1-D circular flexure hinges, but they were excluded from the comparison because this study deals with axial compliance.
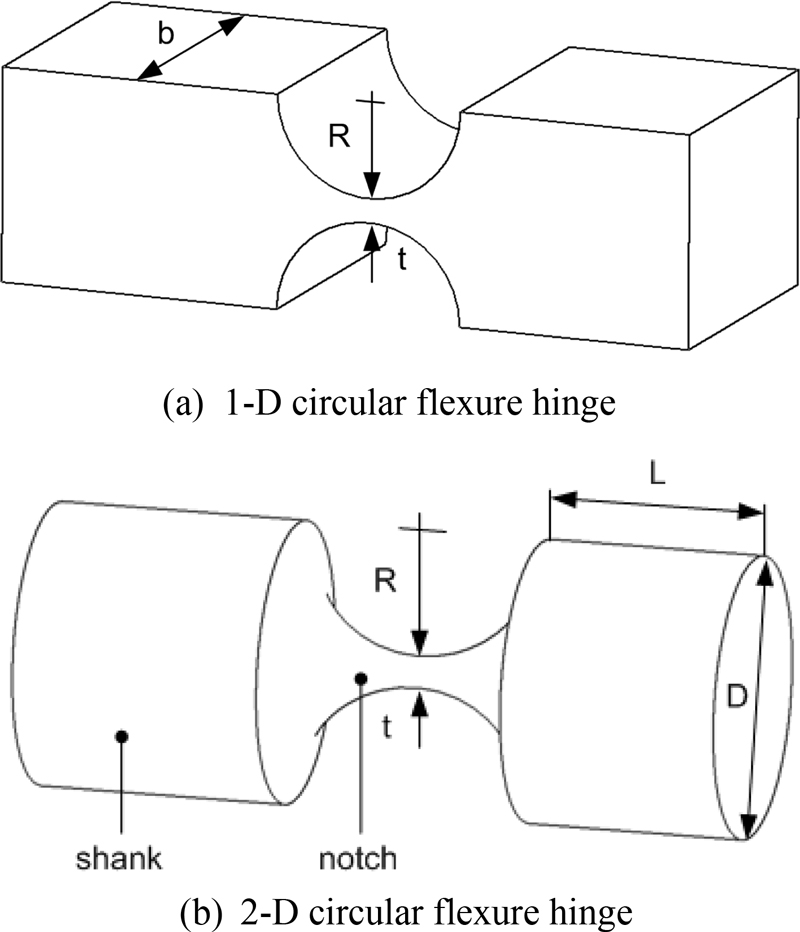
Fig. 1

Circular flexure hinges

KSPE_2025_v42n1_47_f001.jpg
Yong et al. [9] presented an accurate empirical formula for calculating axial and rotational compliance for the 1-D circular flexure hinge in the range of t/R of 0.1 to 0.25, and pointed out that when an axial load is applied to a circular flexure hinge, deformation occurs not only at the notch but also around it, but there is no compliance calculation formula that takes this into account. Li et al. [13] pointed out that a flexible joint with a circular flexure hinge consists of three parts: a notched segment, a segment close to the notch (as much as R), and a segment further away. They obtained an empirical formula for the compliance of a circular flexure hinge by regression to an exponential function from the deformation value calculated by finite element analysis minus the deformation value of the non-notched segment.
We recognized that although a lot of deformation occurs in the region close to the notch, as commonly mentioned by Yong et al. [9] and Li et al. [13], there is no compliance calculation formula that takes this into account. Therefore, our research started with the aim of making theoretical formulas to calculate compliance more accurately by creating a reasonable phenomenon-based model for the region close to the notch.
Meanwhile, studies on the compliance calculation method of 2-D circular flexure hinges have been relatively less frequent than those of 1-D circular flexure hinges, and the compliance calculation formulas of 2-D circular flexure hinges have been derived only by Paros and Weisbord [6] and Lobontiu [8]. Although the compliance calculation formulas developed in these studies have different formula forms, we found that they are the same formulas when the terms were expanded and compared in our study.
Since there was a significant discrepancy between the results obtained from theoretical formulas in previous studies and those obtained from finite element analysis, particularly regarding the axial flexibility of the flexure hinge, this study aims to achieve the following detailed objectives in order to derive more accurate calculation formulas for axial compliance.
First, reasonable assumptions for compliance calculation are established through the stress distribution that occurs when an axial load is applied to the flexure hinge.
Second, phenomenon-based theoretical formulas are derived based on the assumptions.
Third, the accuracy of the newly developed theoretical formulas is verified by comparing them with existing theoretical formulas, and FEA results.
Section 1 is the introduction. Section 2 describes the structure of circular flexure hinges and existing compliance calculation methods. Section 3 derives new theoretical formulas based on the phenomenon caused by axial load. Section 4 verifies the developed formulas through finite element analysis. And Section 5 presents the results and implications of the research.
Ultra-precision stages are mainly used for position control of masks in semiconductor etching processes, and they are in charge of micro-displacement control in a dual motion control consisting of large displacement and micro-displacement. The flexure hinge operates as a precision revolute joint without backlash and microdust due to the absence of lubricant, so it is adopted as an essential component for precision stages.
Circular flexure hinges can be divided into 1-D circular flexure hinges with one rotational degree of freedom and 2-D circular flexure hinges with two rotational degrees of freedom, as shown in Fig. 1.
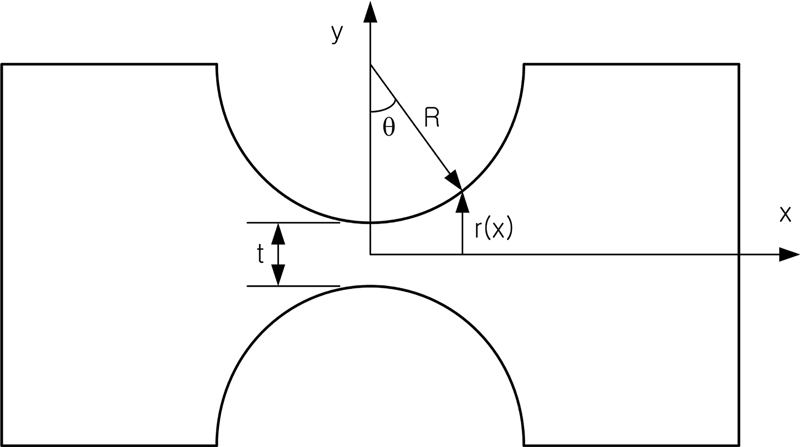
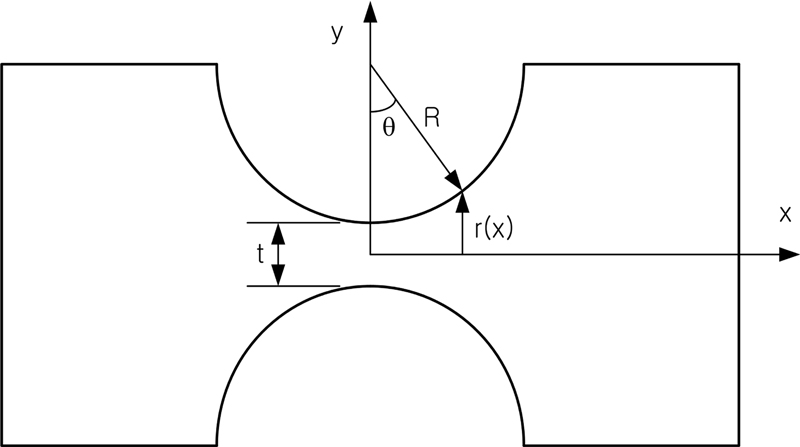
Theoretically, a flexure hinge has a compliance of six components (3 translational + 3 rotational), but the following two components of compliance of a circular flexure hinge are important. The compliance in the axial direction, where the force is transmitted, should be low, and the compliance in the rotational direction, where the intended rotation occurs, should be high. Therefore, in this study, only the axial and rotational compliance of the flexure hinge are considered. The names and coordinates of the variables for the development of the theory are shown in Fig. 2.
Fig. 2

Dimensions and coordinates of the circular flexure hinge

KSPE_2025_v42n1_47_f002.jpg
In this study, the Euler-Bernoulli beam theory was utilized to develop the equations for the following reasons: Since the load changes over time are not abrupt, the effects of rotational inertia can be disregarded. Additionally, for calculating axial and rotational compliance, shear deformation is negligible. When the effects of shear deformation and rotational inertia are excluded from the Timoshenko-Ehrenfest beam theory, it simplifies to the Euler-Bernoulli beam theory.
The compliance of a flexure hinge is based on the following two equations.
(1)
δi=Ci⋅Fi
(2)
θi=Cθi⋅Mi
where i = x, y, z. δ and θrepresent the deformation length and deformation angle, respectively, and F and M represent the force and moment, respectively. The axial compliance Ca and the rotational compliance Cb are calculated as follows [14].
(3)
Ca=1E∫dxA
(4)
Cb=1E∫dxI
where E is the modulus of elasticity, A is the area, and I is the moment of inertia. In Fig. 2, r(x) is as follows:
(5)
rx=t2+R1-1-xR2
With the above basic mechanical equations, previous researchers including Paros and Weisbord [6], Wu and Zhou [7], and Lobontiu et al [8] derived compliance calculation formulas. The formulas are included in Eqs. (A1)-(A14) in the appendix since they are used for comparison. The subscripts are added in the order of ‘compliance direction, degrees of freedom, author’, and the formulas are listed in the order of ‘degrees of freedom, compliance direction, author’ for easy comparison. In addition, the simplified formula of Paros has ‘S’ at the end of the subscript.
Since static linear structural analysis by FEA numerically produces only stress and deformation values under specific loads and constraints, additional application of Eqs. (1) and (2) is required to obtain compliance. In this study, the conditions for FEA are as follows: the left side of the flexure hinge is fixed, and the axial load and bending moment are applied to the right side, respectively. The thickness t of the hinge neck is 1 mm, the width b of the 1-D circular flexure hinge is 10 mm, and the selected material is A7075-T6 with the elastic modulus of 73.013 GPa. The load condition was set so that the maximum stress at the neck of the hinge is within the allowable stress obtained by dividing the yield stress of the material by a safety factor of 2. To obtain the rotational compliance, one end of the shaft was fixed, and a moment (100 N mm for a 1-D circular flexure hinge and 10 N mm for a 2-D flexure hinge) was applied to the opposite end. In addition, to obtain the compressive compliance, one end of the shaft was fixed in the same way, and a force (1000 N for a 1-D circular flexure hinge and 100 N for a 2-D flexure hinge) was applied to the opposite end.
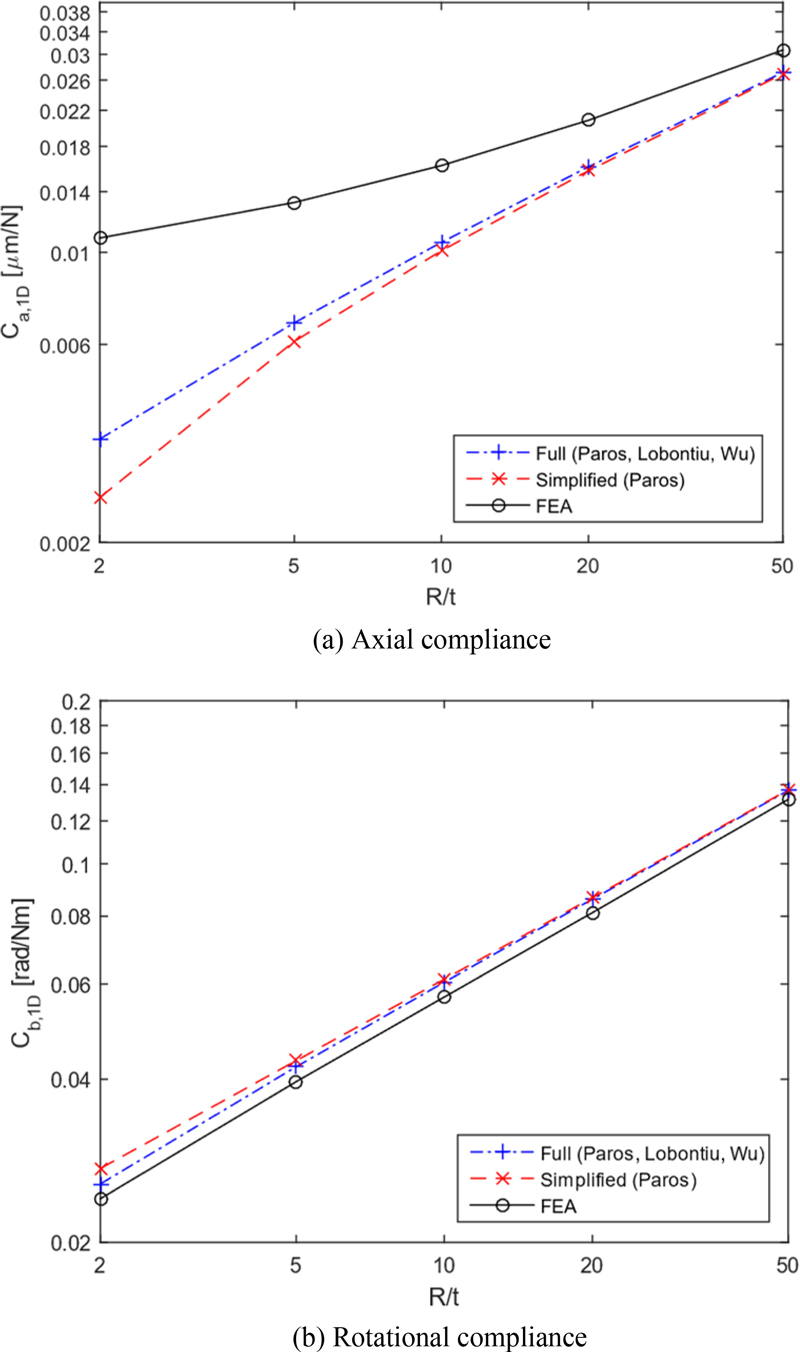
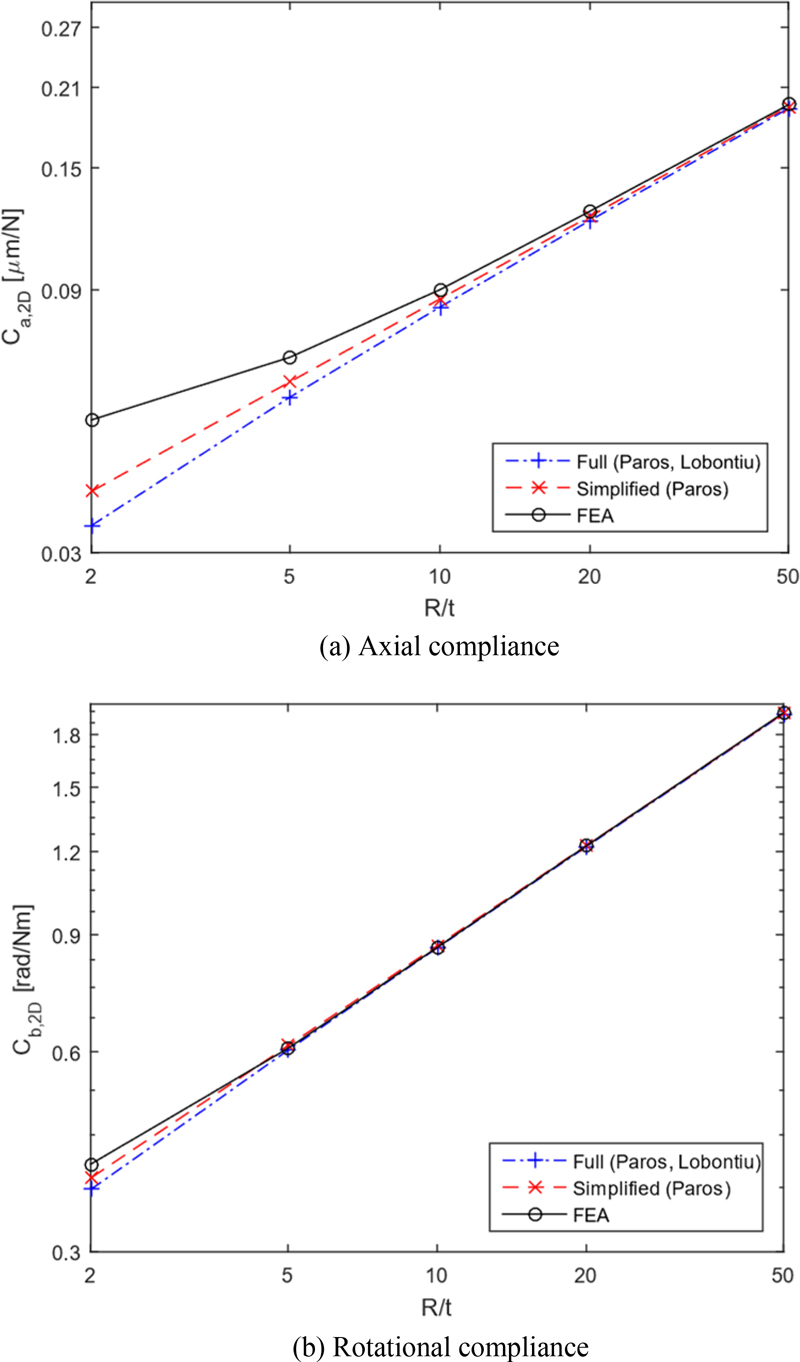
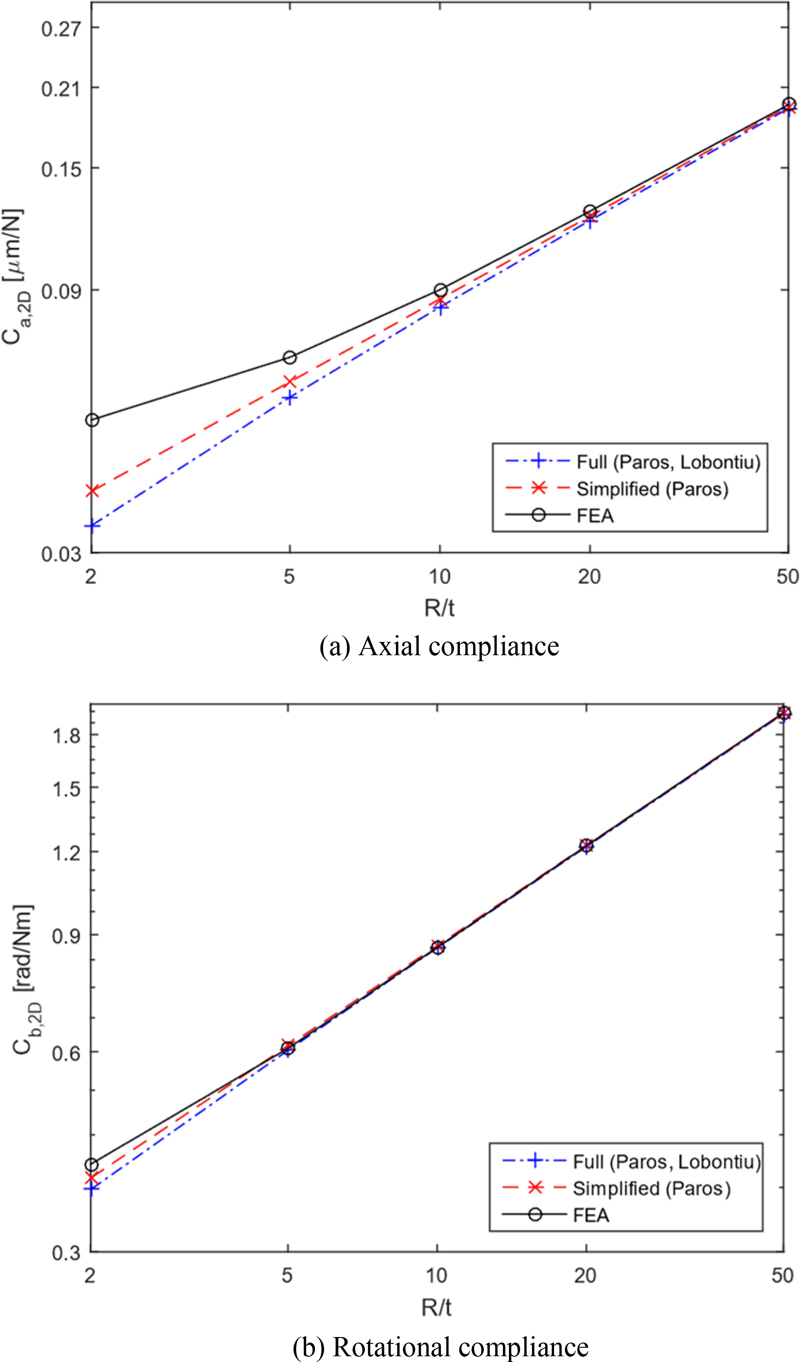
Through Figs. 3 and 4, it is shown that the differences between the calculated values and the finite element analysis values for the rotational compliance are not large, but the differences are large for the axial compliance. Since it is judged that the calculation formulas for the axial compliance need to be improved, and new calculation formulas for the axial compliance are derived in this study.
Fig. 3

Comparison between existing methods and FEA results for the 1-D circular flexure hinge

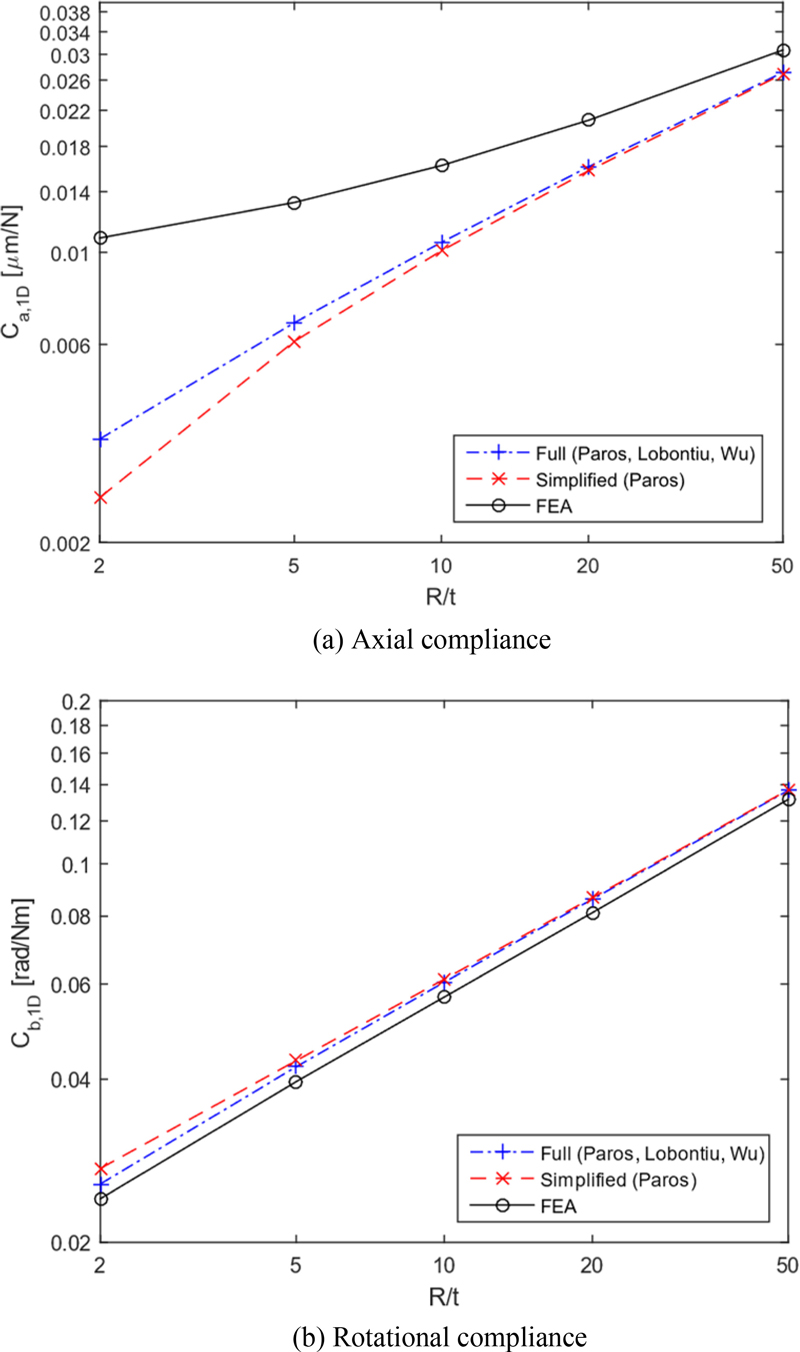
KSPE_2025_v42n1_47_f003.jpg
Fig. 4

Comparison between existing methods and FEA results for the 2-D circular flexure hinge

KSPE_2025_v42n1_47_f004.jpg
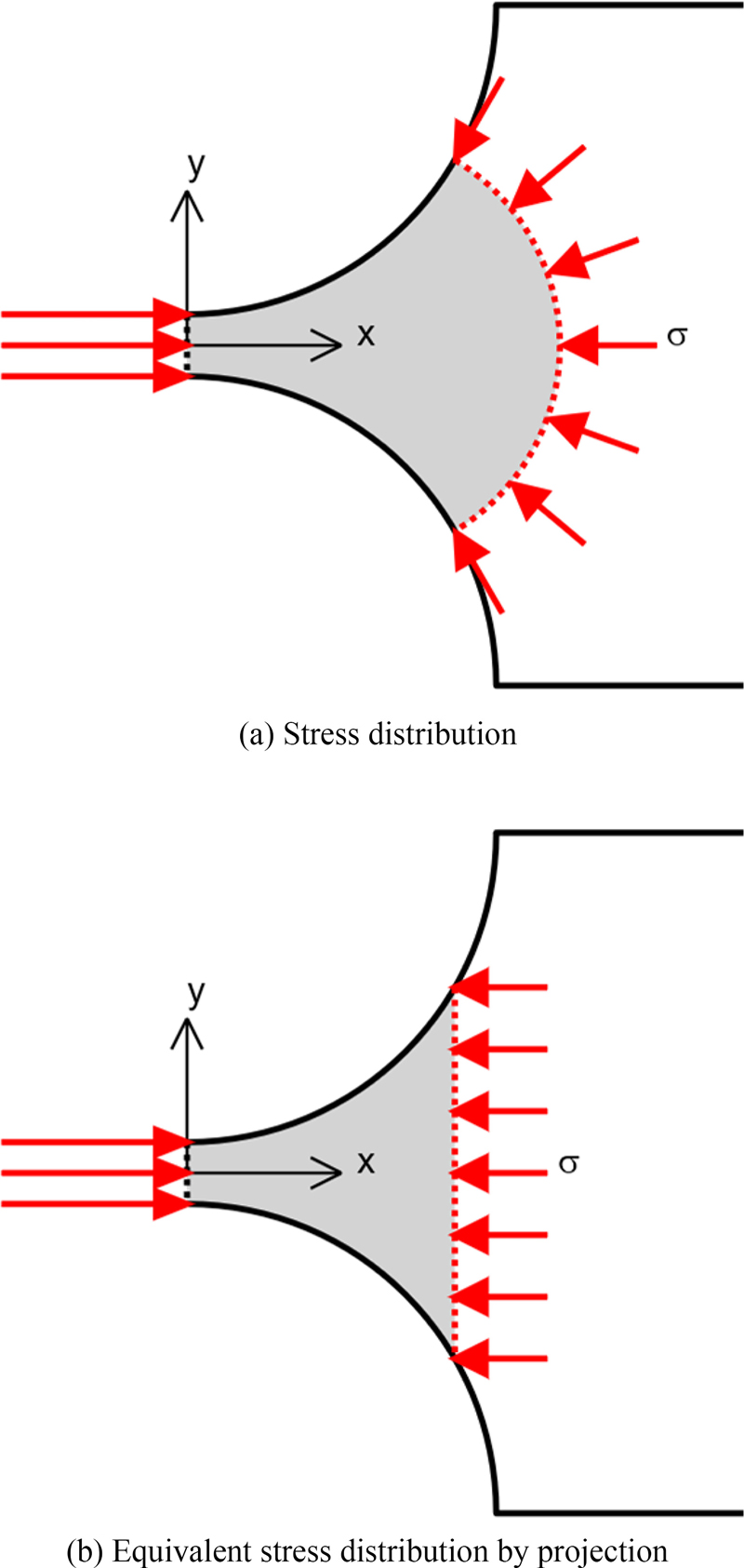
The discrepancy between the results of the theoretical axial compliance calculations and the finite element analysis was examined through an investigation of stress distribution. The stress distribution under axial loading is illustrated in Fig. 5. The stress contour (iso-stress line or surface) is approximately circular and approximately perpendicular to the outline of circular flexure hinge. This phenomenon is clear for the 1-D circular flexure hinge and less clear for the 2-D circular flexure hinge.
Fig. 5

Stress distribution of a 1-D circular flexure hinge when axially extended

KSPE_2025_v42n1_47_f005.jpg
The existing theoretical formulas were obtained by integrating only up to the end of the notch part of the hinge, but the actual stress is widely distributed up to the shank part. It was assumed that a more accurate axial compliance calculation formula could be obtained by deriving the formula considering the shank part. 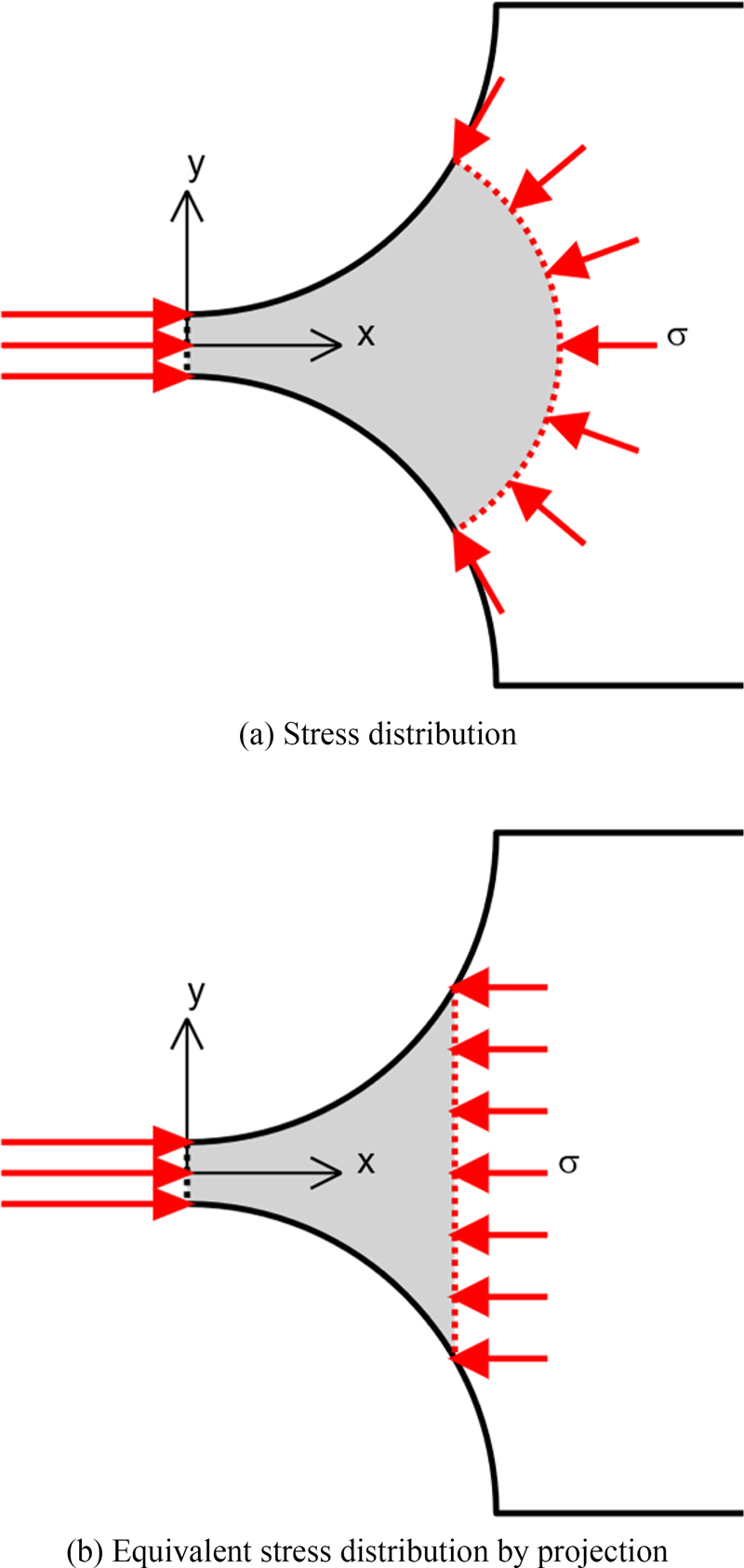The following two assumptions were made based on the insight obtained from the stress contour shown in Fig. 5: First, the stress contour is circular and intersects the outline of the hinge at a right angle. Second, the stress acts perpendicular to the contour plane.
The free body diagram drawn by considering the latter first is as shown in Fig. 6. As can be seen in Figs. 6(a), the stress acting perpendicular to the stress contour can be projected as a stress perpendicular to the plane, as shown in 6(b).
Fig. 6

Free body diagram at a certain stress contour

KSPE_2025_v42n1_47_f006.jpg
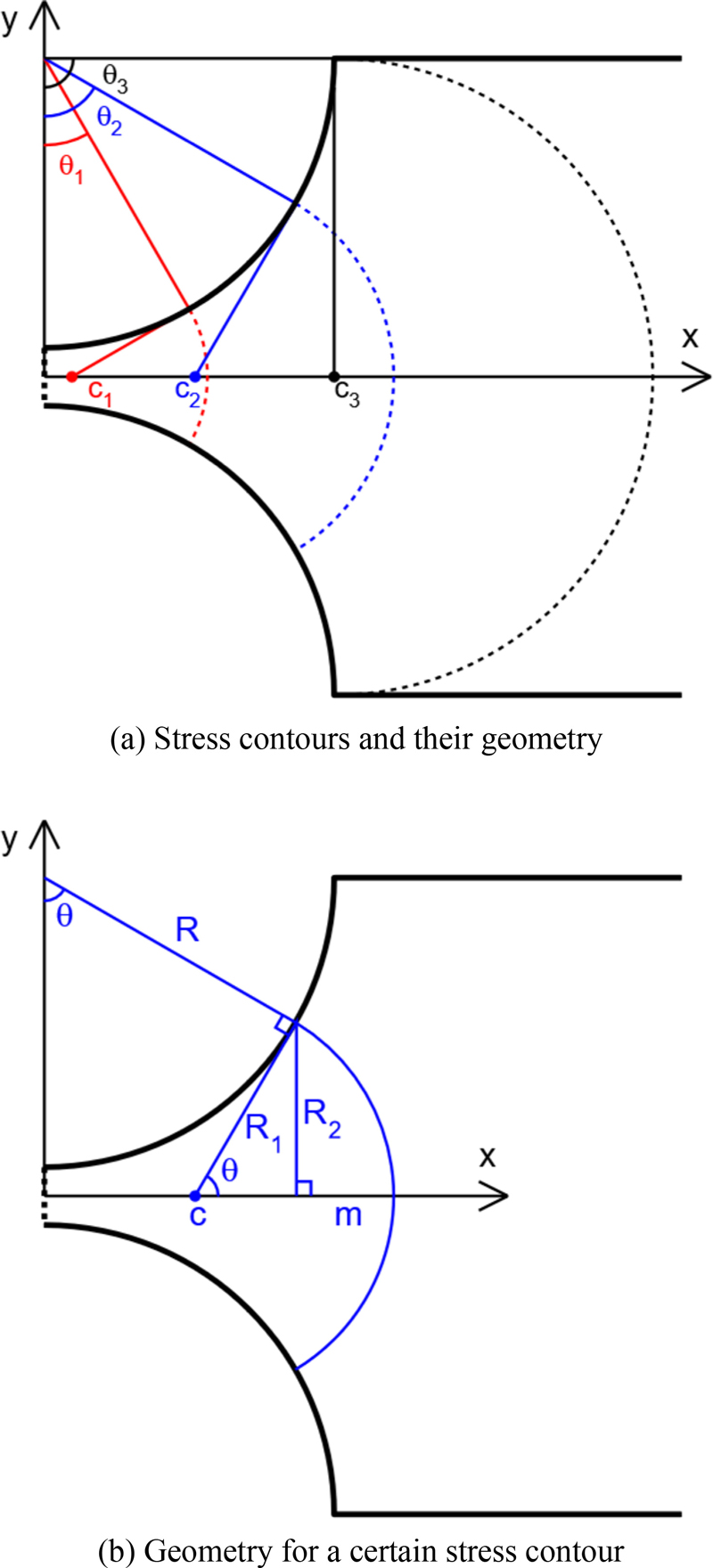
Since the shape of the stress contour (dotted line) in Figs. 7(a) is expressed according to the angle θ, the corresponding geometry for one stress contour is depicted in 7(b).
Fig. 7

Stress contour and geometry

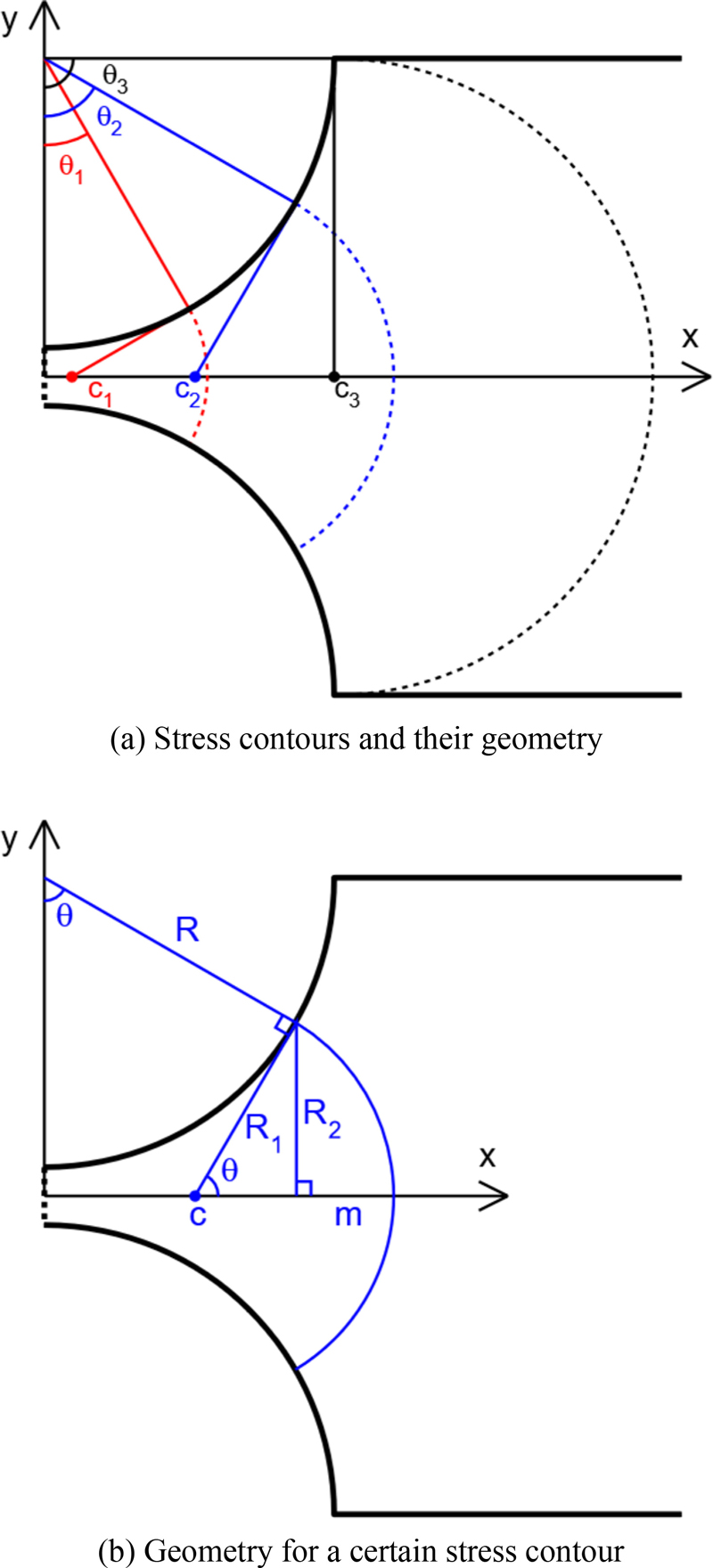
KSPE_2025_v42n1_47_f007.jpg
The equation of the circle forming the outline of a circular flexure hinge is:
(6)
x2+y-t2+R2=R2
Therefore, any point(x, y) on this circle can be expressed as follows:
(7)
x=R sinθ
(8)
y=t2+R(1-cosθ)
Also, the equation of the tangent line at the point(x1, y1) on this circle is as follows.
(9)
x1x+y1-t2+Ry-t2+R=R2
Let the intersection point of this tangent line and the x-axis (y = 0) be (c, 0), then
(10)
c=t2+Rt2+R(1-cosθ)-t24-tRRsinθ
This intersection point (c, 0) becomes the center of the circle forming the stress contour, and the equation of the stress contour circle is as follows (see Fig. 7).
(11)
x-c2+y2=R12
Since the stress contour circle is assumed to be perpendicular to the outline of the hinge, the height m of the arc can be simply expressed as follows by a geometric relationship.
(12)
m=t2+R1-cosθ1-cosθsin⁡θ
Considering that deformation occurs up to the stress contour area of Fig. 7(a), the axial compliance calculation formula of Eq. (3) needs to be corrected. Therefore, if the stress distribution is projected as in Fig. 6, while the area A is the same as in the existing formula, the variable of integration should be replaced from x to x + m.
(13)
dx+m=dθt2+2R11+cosθ
Therefore, by replacing dx in Eq. (3) with d(x + m) in Eq. (13), we can obtain the following result.
(14)
Ca=1E∫1At2+2R11+cosθdθ
The axial compliance formulas for the 1-D flexure hinge and 2-D flexure hinge obtained by calculating the integral of the above equation are Eqs. (15) and (16), respectively.
(15)
Ca,1D=1bE1+4s4s+1arctan⁡4s+1
(16)
Ca,2D=4πEt4s+1×1+4s22s+1+8ss+1arctan4s+14s+1
where s = R / t.
Finite element analysis is performed to verify the performance of the newly developed axial compliance formulas of Eqs. (15) and (16). The circular flexure hinge used in the finite element analysis was set to have a length of one end of the shaft excluding the notch of 120 mm, and the height (at 1-D circular flexure hinge) or diameter (at 2-D circular flexure hinge) of the shaft was set to 101 mm, which was set to a sufficiently large value compared to the neck of the notch so that the deformation of the shank did not affect the overall analysis results. The thickness of the neck of the notch was fixed to 1 mm, and the radius of the circular notch was determined so that R/t was 2, 5, 10, 20, and 50. The grid was created so that the size of one side of the grid was smaller than the thickness t of the hinge.
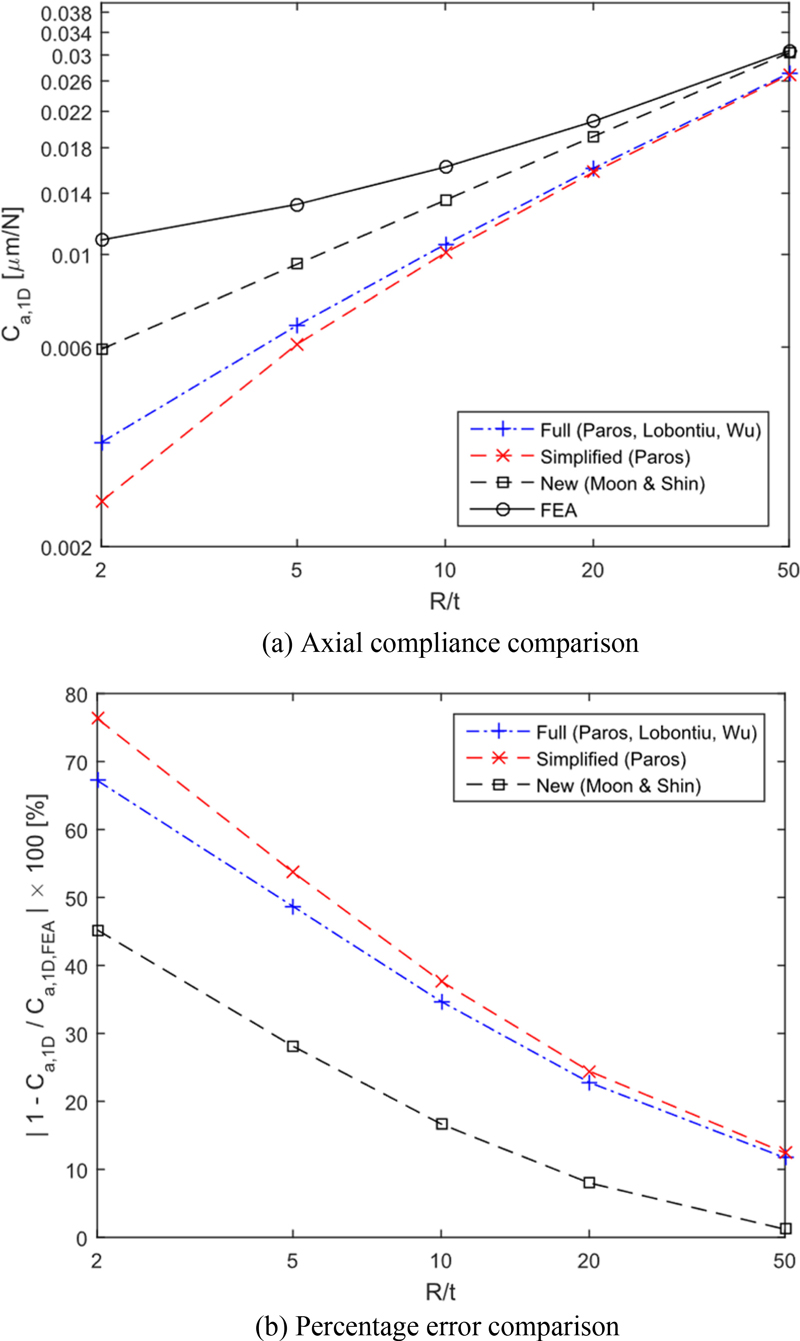
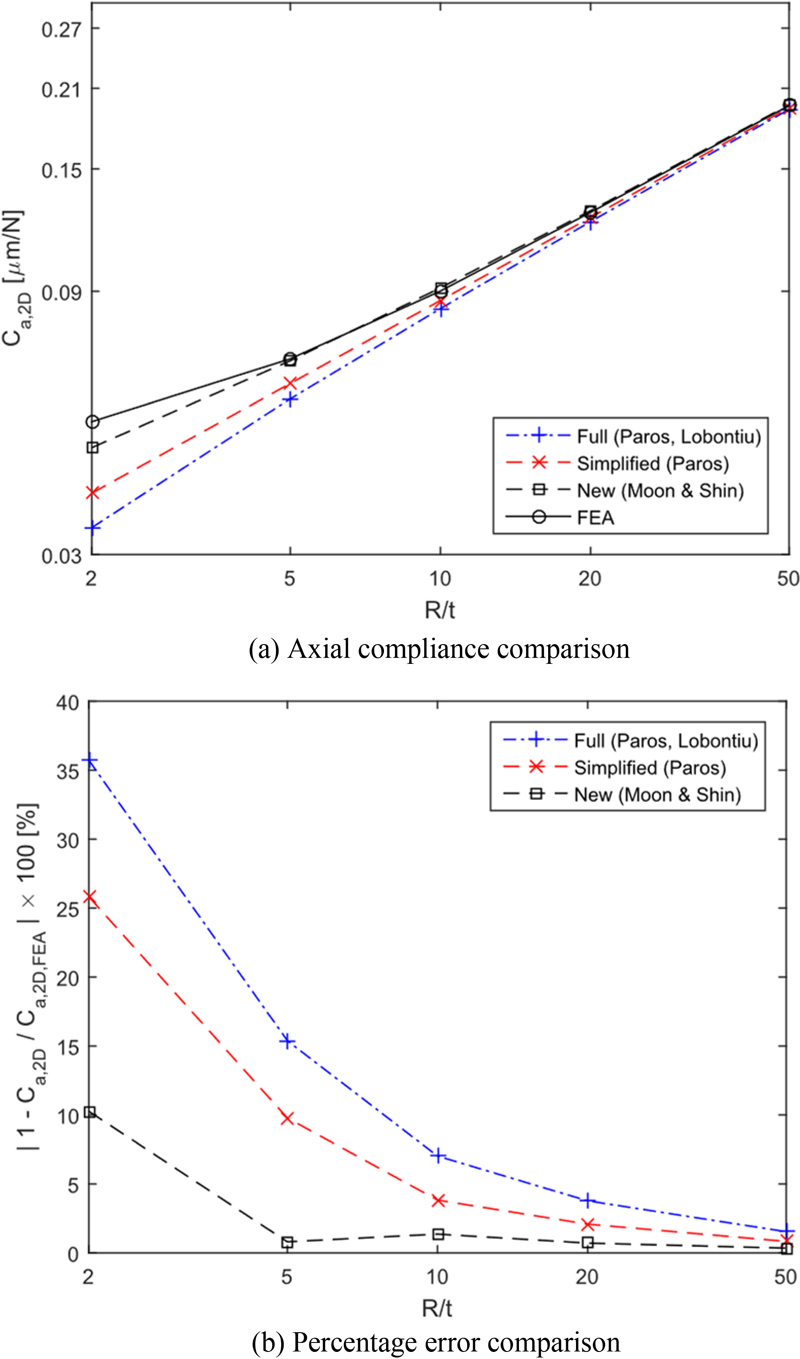
The results of comparing the existing methods and the new method developed in this study with the finite element analysis results are shown in Tables 1 and 2. In Figs. 8 and 9, the percent errors compared with finite element analysis are shown for the 1-D and 2-D circular flexure hinges.
Table 1

Axial compliance values of the 1-D circular flexure hinge

(unit: μm/N)
Table 1
R/t 2 5 10 20 50
Full formula (Paros, Wu, Lobontiu) 3.551E-03 6.764E-03 1.057E-02 1.607E-02 2.713E-02
Simplified formula (Paros) 2.565E-03 6.101E-03 1.009E-02 1.572E-02 2.691E-02
New formula 5.932E-03 9.475E-03 1.348E-02 1.915E-02 3.036E-02
FEA result 1.023E-02 1.276E-02 1.556E-02 2.051E-02 2.994E-02
Table 2

Axial compliance values of the 2-D circular flexure hinge

(unit: μm/N)
Table 2
R/t 2 5 10 20 50
Full formula (Paros, Lobontiu) 3.357E-02 5.745E-02 8.375E-02 1.204E-01 1.923E-01
Simplified formula (Paros) 3.874E-02 6.125E-02 8.662E-02 1.225E-01 1.937E-01
New formula 4.686E-02 6.735E-02 9.129E-02 1.260E-01 1.960E-01
FEA result 5.222E-02 6.789E-02 9.007E-02 1.251E-01 1.953E-01
Fig. 8

Axial compliances of the 1-D circular flexure hinge

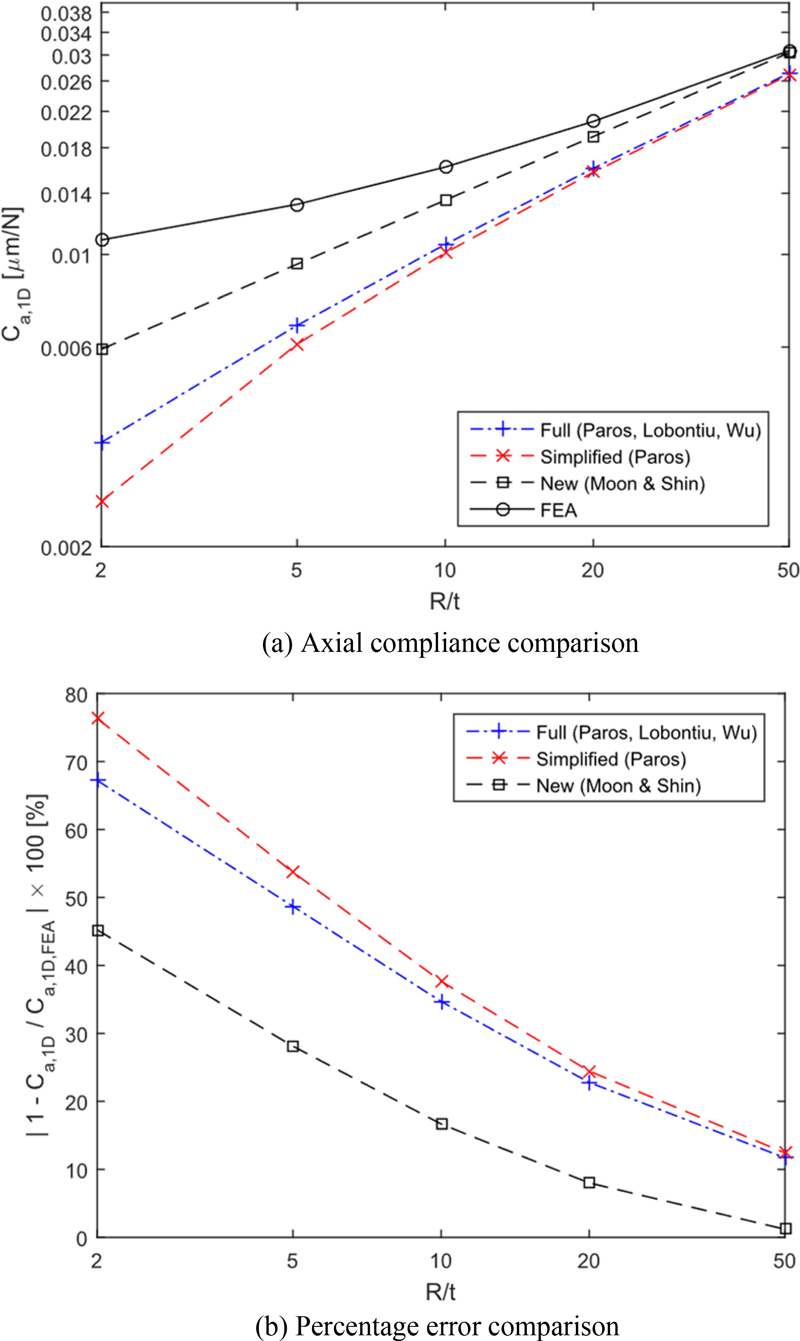
KSPE_2025_v42n1_47_f008.jpg
Fig. 9

Axial compliances of the 2-D circular flexure hinge

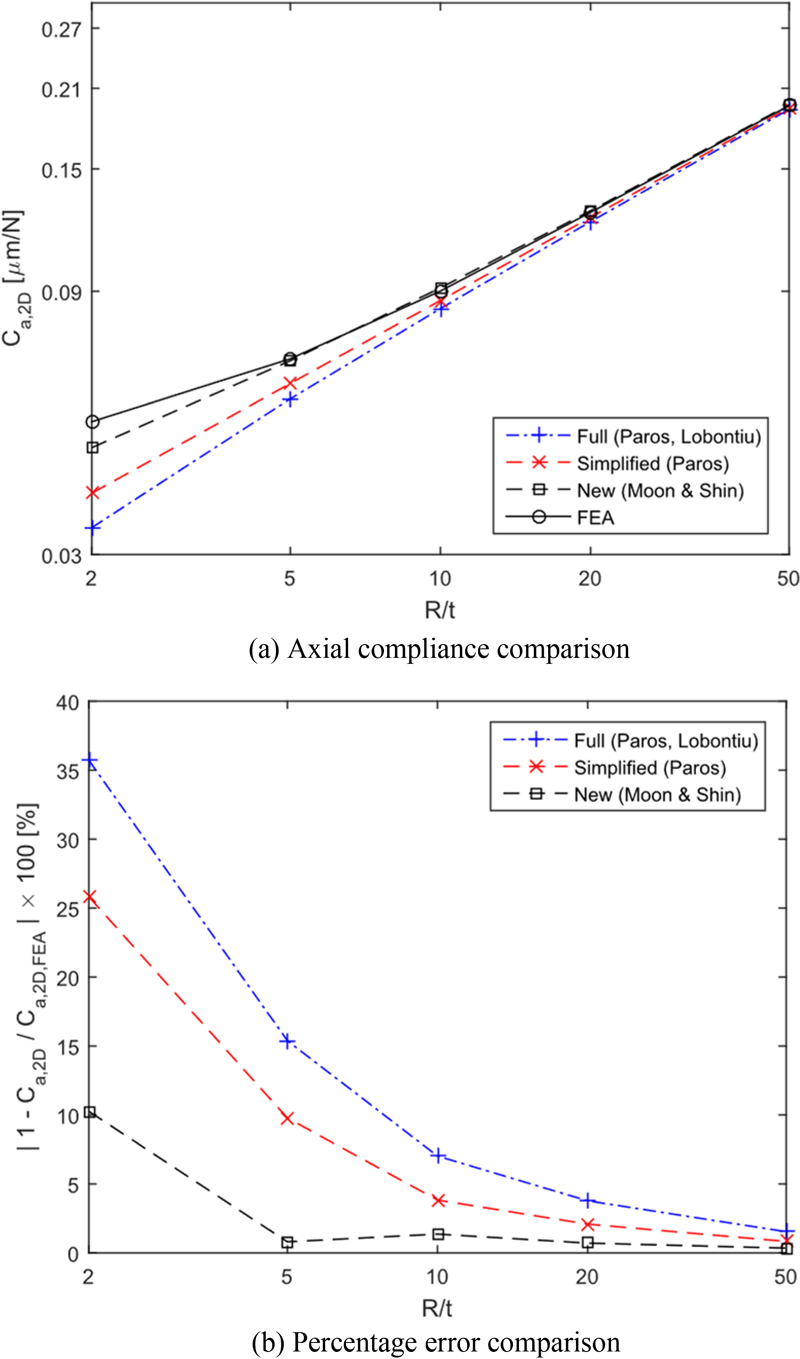
KSPE_2025_v42n1_47_f009.jpg
The performance of the newly developed method was evaluated by the percentage error to see how close the results by the developed compliance formulas are to the finite element analysis results. The results are as follows: For the 1-D circular flexure hinge, the developed calculation formulas are 10.5 to 31.1% closer to the finite element analysis results across all values of R/t. For the 2-D circular flexure hinge, the formulas are 0.48 to 25.4% closer to the finite element analysis results for all values of R/t. These findings demonstrate that the newly developed formulas provide superior compliance calculation performance compared to existing formulas. Furthermore, the new formulas are simpler in form, enhancing their ease of use.
Firstly, we found a significant discrepancy between the axial compliance values of the circular flexure hinge obtained from existing theoretical formulas and those from finite element analysis (FEA). Secondly, reasonable assumptions were established for compliance calculation based on the stress distribution under axial load: the stress contour is circular and meets the outline of the hinge at a right angle, and the stress acts normally to the contour plane. Thirdly, axial compliance formulas for both 1-D and 2-D circular flexure hinges, presented in Eqs. (15) and (16), were derived based on these assumptions. Fourthly, the superiority of the developed theoretical formulas over existing ones was confirmed by evaluating the percent error relative to FEA results. Lastly, the newly proposed compliance formulas for circular flexure hinges are anticipated to be highly beneficial for industrial applications due to their accuracy and simplicity, potentially reducing both time and cost in design processes.
  • 1.
    Moon, J.-H., Pahk, H. J., Lee, B.-G., (2011), Design, modeling, and testing of a novel 6-DOF micropositioning stage with low profile and low parasitic motion, International Journal of Advanced Manufacturing Technology, 55(1-4), 163-176.
    10.1007/s00170-010-3033-4
  • 2.
    Shin, H., Moon, J.-H., (2014), Design of a double triangular parallel mechanism for precision positioning and large force generation, IEEE/ASME Transactions on Mechatronics, 19(3), 862-871.
    10.1109/TMECH.2013.2261822
  • 3.
    Yong, Y. K., Moheimani, S. O. R., Kenton, B. J., Leang, K. K., (2012), Invited review article: high-speed flexure-guided nanopositioning: mechanical design and control issues, Review of Scientific Instruments, 83(12), 121101.
    10.1063/1.4765048
  • 4.
    Moon, J.-H., (2022), Analysis of the cylindrical flexure hinges with circular notches, Journal of the Korean Society for Precision Engineering, 39(2), 151-157.
    10.7736/JKSPE.021.112
  • 5.
    Shin, H.-P., Moon, J.-H., (2023), Analysis on elliptic and parabolic 2-DOF flexure hinges for spatial positioning stages, Journal of the Korean Society for Precision Engineering, 40(3), 229-236.
    10.7736/JKSPE.022.120
  • 6.
    Paros, J. M., Weisbord, L., (1965), How to design flexure hinges, Machine Design, 37(8), 151-156.
  • 7.
    Wu, Y., Zhou, Z., (2002), Design calculations for flexure hinges, Review of Scientific Instruments, 73(9), 3101-3106.
    10.1063/1.1494855
  • 8.
    Lobontiu, N., (2002), Compliant mechanisms: design of flexure hinges, CRC press.
    10.1201/9781420040272
  • 9.
    Yong, Y. K., Lu, T.-F., Handley, D. C., (2008), Review of circular flexure hinge design equations and derivation of empirical formulations, Precision Engineering, 32(2), 63-70.
    10.1016/j.precisioneng.2007.05.002
  • 10.
    Smith, S. T., Chetwynd, D. G., Bowen, D. K., (1987), Design and assessment of monolithic high precision translation mechanisms, Journal of Physics E, 20(8), 977-983.
    10.1088/0022-3735/20/8/005
  • 11.
    Tseytlin, Y. M., (2002), Notch flexure hinges: an effective theory, Review of Scientific Instruments, 73(9), 3363-3368.
    10.1063/1.1499761
  • 12.
    Schotborgh, W., Kokkeler F., Trangter, H., van Houten, F., (2005), Dimensionless design graphs for flexure elements and a comparison between three flexure elements, Precision Engineering, 29(1), 41-47.
    10.1016/j.precisioneng.2004.04.003
  • 13.
    Li, T.-M., Zhang, J.-L., Jiang, Y., (2015), Derivation of empirical compliance equations for circular flexure hinge considering the effect of stress concentration, International Journal of Precision Engineering and Manufacturing, 16(8), 1735-1743.
    10.1007/s12541-015-0228-5
  • 14.
    Crandall, S. H., Dahl, N. C., Lardner, T. J., Sivakumar, M. S., (2012), An introduction to mechanics of solids: (In SI Units), 3rd Ed., McGraw-Hill.
Jun-Hee Moon
KSPE_2025_v42n1_47_bf001.jpg
Associate Professor in the Department of Mechanical Engineering, Yuhan University, Gyeonggi-do, South Korea. His research interests include the design and control of flexure linkages and micro-positioning stages.
Hyun-Pyo Shin
KSPE_2025_v42n1_47_bf002.jpg
Associate Professor in the School of Robot and Automation Engineering, Dongyang Mirae University, Seoul, South Korea. His current research interests include the design of redundantly actuated parallel mechanisms and ultra-precision positioning stages based on flexure hinges.
APPENDIX

A.1 Compliance Formulas for the 1-D Circular Flexure Hinge

(1) Axial compliance formulas for the 1-D circular flexure hinge by Paros
(A1)
Ca,1D,Pa=1Eb-2tan-1γ-β1-1+β-γ2+21+β2β+β2tan-12+ββ×γ-β1-1+β-γ2
where β=t2R,γ=1+β
by Lobontiu
(A2)
Ca,1D,Lo=1Eb22R+tt4R+tarctan4Rt+1-π2
by Wu
(A3)
Ca,1D,Wu=1Eb22s+14s+1arctan4s+1-π2
where S = R / t
(2) Rotational compliance formulas for the 1-D circular flexure hinge by Paros
(A4)
Cb,1D,Pa=32EbR212β+β21+βγ2+3+2β+β2γ2β+β2×1-1+β-γ2+6(1+β)2β+β23/2×tan-12+ββ×γ-β1-1+β+γ2
where β=t2R,γ=1+β
by Lobontiu
(A5)
Cb,1D,Lo=24REbt32R+t4R+t3t4R+t6R2+6Rt+t2+6R2R+t2t4R+tarctan4Rt+1
by Wu
(A6)
Ca,1D,Wu=12EbR22s36s2+4s+12s+14s+12+12s42s+14s+152arctan⁡4s+1
where S = R / t

A.2 Compliance Formulas for the 2-D Circular Flexure Hinge

(1) Axial compliance formulas for the 2-D circular flexure hinge by Paros
(A7)
Cb,1D,Pa=2πER22β+β23/2tan-12+ββγ1-1+β-γ2+(1+β)2β+β2γ1-1+β-γ2
by Lobontiu
(A8)
Ca,2D,Lo=8RπEt2t4R+t+4Rt4R+t3arctan1+4Rt
(2) Rotational compliance formulas for the 2-D circular flexure hinge
by Paros
(A9)
Cb,2D,Pa=83πER32β+β2×1+βγ3+21+β2+32γ22β+β2+21+β3+13(1+β)22β+β22γ×1-1+β-γ2+121+β2+32β+β25/2tan-1⁡2+ββγ-β1-1+β-γ2
by Lobontiu
(A10)
Cb,2D,Lo=128R3πEt4t120R4+176R3t+92R2t2+24Rt3+3t42R+t24R+t3+24R5R2+4Rt+t2t4R+t7arctan1+4Rt

A.3 Simplified Compliance Formulas for the Circular Flexure Hinge (by Paros)

(1) Axial compliance formulas for the 1-D circular flexure hinge (by Paros)
(A11)
Ca,1D,PaS=1EbπRt12-2.57
(2) Rotational compliance formulas for the 1-D circular flexure hinge (by Paros)
(A12)
Cb,1D,PaS=9π2Ebt2Rt12
(3) Axial compliance formulas for the 2-D circular flexure hinge (by Paros)
(A13)
Ca,2D,PaS=2EtRt12
(4) Rotational compliance formulas for the 2-D circular flexure hinge (by Paros)
(A14)
Cb,2D,PaS=20Et3Rt12

Download Citation

Download a citation file in RIS format that can be imported by all major citation management software, including EndNote, ProCite, RefWorks, and Reference Manager.

Format:

Include:

Derivation and Verification of Novel Phenomenon-based Theoretical Formulas for the Axial Compliance of Circular Flexure Hinges
J. Korean Soc. Precis. Eng.. 2025;42(1):47-55.   Published online January 1, 2025
DOI: https://doi.org/10.7736/JKSPE.024.108
Download Citation

Download a citation file in RIS format that can be imported by all major citation management software, including EndNote, ProCite, RefWorks, and Reference Manager.
Format:
Include:
Derivation and Verification of Novel Phenomenon-based Theoretical Formulas for the Axial Compliance of Circular Flexure Hinges
J. Korean Soc. Precis. Eng.. 2025;42(1):47-55.   Published online January 1, 2025
DOI: https://doi.org/10.7736/JKSPE.024.108
Close

Figure

  • 0
  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
Derivation and Verification of Novel Phenomenon-based Theoretical Formulas for the Axial Compliance of Circular Flexure Hinges
Image Image Image Image Image Image Image Image Image
Fig. 1 Circular flexure hinges
Fig. 2 Dimensions and coordinates of the circular flexure hinge
Fig. 3 Comparison between existing methods and FEA results for the 1-D circular flexure hinge
Fig. 4 Comparison between existing methods and FEA results for the 2-D circular flexure hinge
Fig. 5 Stress distribution of a 1-D circular flexure hinge when axially extended
Fig. 6 Free body diagram at a certain stress contour
Fig. 7 Stress contour and geometry
Fig. 8 Axial compliances of the 1-D circular flexure hinge
Fig. 9 Axial compliances of the 2-D circular flexure hinge

Fig. 1

Fig. 2

Fig. 3

Fig. 4

Fig. 5

Fig. 6

Fig. 7

Fig. 8

Fig. 9

Derivation and Verification of Novel Phenomenon-based Theoretical Formulas for the Axial Compliance of Circular Flexure Hinges
R/t 2 5 10 20 50
Full formula (Paros, Wu, Lobontiu) 3.551E-03 6.764E-03 1.057E-02 1.607E-02 2.713E-02
Simplified formula (Paros) 2.565E-03 6.101E-03 1.009E-02 1.572E-02 2.691E-02
New formula 5.932E-03 9.475E-03 1.348E-02 1.915E-02 3.036E-02
FEA result 1.023E-02 1.276E-02 1.556E-02 2.051E-02 2.994E-02
R/t 2 5 10 20 50
Full formula (Paros, Lobontiu) 3.357E-02 5.745E-02 8.375E-02 1.204E-01 1.923E-01
Simplified formula (Paros) 3.874E-02 6.125E-02 8.662E-02 1.225E-01 1.937E-01
New formula 4.686E-02 6.735E-02 9.129E-02 1.260E-01 1.960E-01
FEA result 5.222E-02 6.789E-02 9.007E-02 1.251E-01 1.953E-01
Table 1 Axial compliance values of the 1-D circular flexure hinge (unit: μm/N)
Table 2 Axial compliance values of the 2-D circular flexure hinge (unit: μm/N)

Table 1

Table 2

JKSPE : Journal of the Korean Society for Precision Engineering

ABOUT

BROWSE ARTICLES

EDITORIAL POLICIES

FOR CONTRIBUTORS

© Korean Society for Precision Engineering.