ABSTRACT
Centrifugal compressor is a device that converts kinetic energy to increase the air pressure. It rotates at a high speed of up to 200,000 RPM and directly affects aerodynamic noise. Various studies have already been conducted, but the direct calculation method of acoustics based on the unsteady solution is inefficient because it requires a lot of resources and time. Therefore, flow characteristics and numerical comparison according to various aerodynamic factors predicted as a cause of noise generation were analyzed in this study based on the steady solution. High-frequency noise was calculated locally near the asymmetric flow properties. Vortex and turbulent kinetic energy were generated at similar locations. Among static components, a large-sized vortex of 3.48×107 s-1 was distributed at the location where the rotational flow around the compressor wheel combined with the inlet suction flow. In addition, a locally high vortex of 8.16×105 s-1 was distributed around the balancing cutting configurations that cause asymmetric flow characteristics. Analysis of these factors and causes that directly affect noise can be efficiently improved in the pre-design stage. Therefore, the efficient design methodology for centrifugal compressors that considers both performance and noise is expected based on the results of this study.
-
KEYWORDS: High-speed turbomachinery, Centrifugal compressor, High-frequency noise, Computational fluid dynamics, Computational aero-acoustics, Flow-induced noise
-
KEYWORDS: 초고속 터보기계, 원심 압축기, 고주파 소음, 전산유체역학, 전산공력음향학, 유동유발소음
1. 서론
원심 압축기는 고속으로 회전하는 임펠러(Impeller)의 원심력을 활용하여 유체의 운동에너지를 압력에너지로 변환시키는 장치이다. 일반적인 압축기에 비해 단당 압축비가 높고, 용이한 생산성 등의 장점으로 산업용 기계로부터 가전제품, 발전/항공용 엔진에 이르기까지 다양한 산업 분야에서 활용되고 있다. 특히 전통적인 내연기관 자동차의 엔진 성능 및 효율 개선을 목적으로 사용되던 초고속 원심 압축기는 친환경 자동차 시장의 확산과 더불어 최근 개발되는 전기 자동차의 연료전지 시스템 구성에도 넓게 활용된다
[1].
최근 원심 압축기는 소형화와 생산성 등 그 장점을 극대화하는 방향으로 개발이 이루어지고 있다. 하지만, 최대 200,000 RPM 이상의 높은 속도로 회전하는 소형 압축기는 불규칙한 유동 특성으로 인하여 휘슬(Whistle) 소음과 톤(Tone) 소음 등 10여 가지 이상의 복합적인 특성의 소음이 발생한다
[2-
4]. 원심 압축기의 소음을 이해하기 위해서는 초고속으로 회전하는 압축기에서 소음을 유발하는 유동 특성 파악이 선행되어야 한다.
소형 압축기의 성능 특성을 수치 또는 실험적으로 파악하기 위해 다양한 연구들이 수행되었다. 차량용 압축기 성능에는 임펠러와 블레이드 등 동적 구성품과 더불어 볼류트(Volute)와 하우징 등 정적인 부품들도 지배적인 영향을 미친다
[5]. 전체 시스템을 포함한 압축기 성능을 분석하기 위해 Tianjun 등은 3-원호 단면 오버형 볼류트의 두가지 형태에 대해 유동 특성을 분석하였다
[6]. 차량용 압축기의 성능과 효율을 수치적으로 예측하기 위해 Lee 등은 해석 및 유한요소 모델링을 개발하였고
[7], Song 등은 리니어 컴프레서 효율을 전산 유체 해석적으로 분석하였다
[8]. 또한, 복합적인 분석이 용이한 전산 유체역학(Computational Fluid Dynamics, CFD)의 장점을 활용하여 An 등은 압축기의 효율을 향상시키는 연구를 수행하였다
[9]. 전산유체역학에 기반하여 수치적으로 공기역학적 특성을 예측하는 방법은 경제적이고, 효율적인 성능 예측이 가능하다는 장점이 있다. 또한, 적은 비용으로 복합적 조건과 다양한 형상에 대한 예측이 가능하기 때문에 터빈 회전수 변화를 예측하는 등 효율적인 방법론으로 제시되고 있다
[10].
최근 압축기에서는 기계적인 효율 및 성능과 더불어 새로운 성능 인자인 소음과 진동의 중요성이 대두되고 있다. 이는 비교적 기술 수준을 확보한 성능 목표치에 비해 소음과 진동에 대한 이해는 다소 부족하며, 특히 동적인 구성품의 안정적 작동과 정숙성 등의 가치가 친환경 자동차, 산업용 기계, 가전제품 등의 분야에서 더욱 중요시 여겨지기 때문이다. 이러한 유동 유발 소음을 분석하기 위해 Xu 등은 압축기 내부에서 발생하는 불규칙한 유동 특성에 의한 소음과 진동을 분석하였다
[11]. Semlitsch 등은 소음과 진동 현상을 유발하는데 기여하는 원심 압축기 입구의 불규칙한 비정상 유동 특성에 대해 분석하였다
[12]. 이는 역류를 발생시키기 때문에 성능뿐만 아니라 소음 측면에서도 악영향을 미칠 것으로 예측하였다. 최근 압축기에서는 다양한 방법론에 기반하여 성능과 소음을 개선하려는 복합적 연구들이 수행되고 있다
[13]. 하지만, 수치적인 방법에 기반하여 압축기성능을 개선하는 연구에 비해 압축기의 소음 특성을 전산 공력 음향학(Computational Aeroacoustics, CAA)적으로 직접 예측하는 것은 여전히 많은 계산 비용이 소모된다.
본질적으로 비정상 유동을 다루는 음향학 측면에서 원심 압축기 소음 특성을 직접적으로 분석하는 방법은 기하급수적인 자원이 요구된다. 이는 투입되는 자원에 비해 효율적인 예측이 어렵기 때문에 산업계의 개발 과정에서 직접적으로 사용되기에는 한계가 있다. 따라서, 본 연구에서는 정상해에 기반하여 차량용 원심 압축기 소음의 원인을 효율적으로 분석하였다. 적절한 방법에 근거하여 원심 압축기의 정상해 기반 소음을 예측하기 위해서는 소음 특성에 대한 이해가 선행되어야 한다. 원심 압축기에서는 급격한 압력 변동과 복잡한 날개 끝에서 발생하는 와도, 난류 운동에너지 등 유동 소음을 유발하는 공기역학적 특성들이 복합적으로 발생한다
[14]. 정상해 기반의 소음 분석은 공기역학적 비정상 항들을 소거하기 때문에 주파수 특성이 반영되지 않는다는 한계가 있다. 따라서, BPF 소음과 특정 Tone 소음 등 주파수가 고려된 소음 특성 분석은 적절하지 않다. 다만, 초기 설계 또는 신속한 개발이 요구되는 산업계 등에서 압축기, 하우징 등의 형상과 운용 조건에 따른 효율적 예측이 가능하다는 막강한 이점이 있다. 이에, 본 연구에서는 소음에 영향을 미칠 것으로 사료되는 유동 특성을 분석하여, 소음 발생의 원인이 되는 공기역학적 인자들을 제시하였다. 이를 바탕으로 원심 압축기 소음을 효과적으로 분석하는 방법론을 제시하는데 목표를 두었다.
2. 설계 및 수치해석
2.1 해석 모델링
본 연구에서 사용된 원심 압축기는 국내 K(社)의 중형급 차량용 터보 압축기 모듈을 활용하였다.
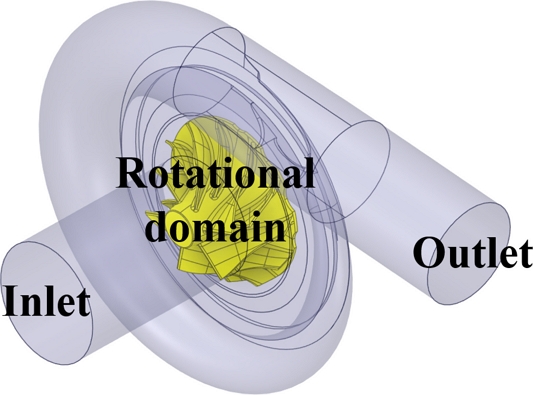
Fig. 1(a)는 터빈 부와 메인 축을 제외한 원심 압축기 하우징의 형상이다. 하우징은 디퓨저 효과로 압력에너지 증대를 위한 목적으로 비대칭 형상으로 설계된다. 그렇기 때문에 하우징 내부의 유동 특성도 의도적으로 비대칭하게 발생한다. 내부에는 터빈으로 전달받은 운동에너지를 압력에너지로 변환하기 위해 축으로 연결된 압축기 임펠러가 있다. 임펠러는
Fig. 1(b)와 같이 생산 공정으로 발생하는 질량 불균형 현상을 개선하기 위해 밸런싱 컷팅(Balancing Cutting)이 적용된다. 밸런싱 컷팅은 양산 과정에서 발생하는 생산 공학적 질량 불균형 현상을 개선하기 위한 목적이다. 하지만, 형상에 의해 불규칙한 유동 특성을 야기하여 소음의 측면에서 불리한 영향을 미친다. 이러한 영향을 분석하기 위해 본 연구에서는 밸런싱 컷팅이 포함된 임펠러를 사용하였다.
Fig. 1Centrifugal compressor in high-speed turbomachinery

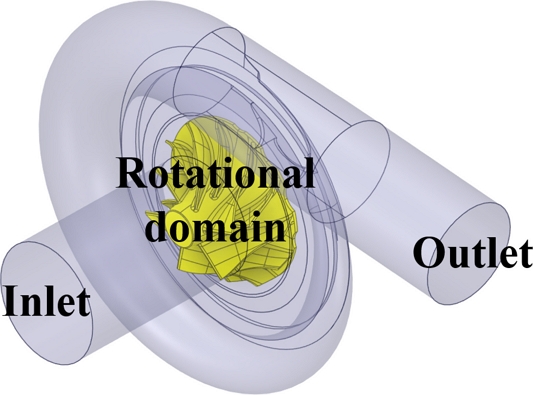
수치해석적으로 압축기 내부 유동 특성을 분석하기 위해 유체가 완전 발달할 수 있도록
Fig. 2의 입출구(Inlet/Outlet) 유동장을 확장하여 완전발달 유동으로 가정하였다. 압축기 내부 임펠러의 회전운동을 계산에 반영하기 위해 유동장을 회전 영역과 비회전 영역으로 분리하여 사용했다. 임펠러를 포함한 최소한의 크기를 회전 유동장(
Fig. 2의 Rotational Domain)으로 설정하여 정상상태 기반 회전 방정식을 계산할 수 있도록 하였고, 하우징을 포함한 그 이외 영역은 비회전 유동장으로 설정하였다. 이는 수치적 연구에서 상이한 지배 방정식을 적용하여 유체의 흐름을 효율적으로 계산될 수 있도록 활용하였다.
Fig. 2Fluid domain with boundary conditions
2.2 격자생성
수치적으로 압축기 유동 특성을 분석하기 위해 생성된 유동장 내에 비정렬 격자를 생성하였다. 입구와 임펠러 인근 회전영역, 출구부로 나누어 전체 유동장 격자를 효과적으로 생성하였다. 사면체 격자를 기본으로 사용하였고, 벽면 경계층 효과를 반영하기 위해 6개의 경계층을 생성하여 Y+를 만족시켰다. 경계층 성장률은 1.2배로 선택하여 격자에 의한 수치해가 없도록 격자를 구성하였다. 효율적인 공력해 도출을 위해 격자 의존도 검사를 수행하였고, 전체 약 369만 개의 격자를 연구에 활용하였다.
2.3 수치해석
정상상태 유동해 기반으로 압축기 내부 유동 특성을 분석하기 위해서 상용 CFD 코드인 ANSYS CFX V18.0를 활용하여 유동장에 대한 계산을 수행하였다. 유체의 지배적인 거동 특성은 아래의 연속 방정식과 운동량 방정식을 활용하여 예측하였다.
여기서,
식(2)의 τ는 응력 텐서로 아래와 같이 정의된다.
유체의 거동을 모사하는
식(1) 및
식(2)의 연속 방정식과 운동량 방정식은 미소 요소에 대한 직선 운동을 가정한다. 본 문제에서는 유체의 회전 운동을 계산하기 위해
식(2)의 방정식을 회전 좌표계에 적용하였다. 또한, 회전 운동을 모사하는 항들이 추가된
식(4)를 사용하였다.
여기서,
a와
α는 유체 요소의 선형 가속도(=
dv/
dt)와 각 가속도(=
dω/
dt)를 표현한다. 이와 더불어 Coriolis 가속도, 구심 가속도를 포함한다. 생성된 유동장 내에서 입구와 출구 유동장은
식(2)의 방정식을 사용하여 유체 운동을 모사하였고, 압축기의 임펠러 인근 유동장은
식(4)의 방정식을 활용하여 유체 회전 운동을 계산하였다. 회전 운동하는 유동장과 비회전 유동장의 효율적인 경계면 데이터 전달을 위해 Frozen Rotor 모델을 계산에 적용하였다.
고속으로 회전하는 원심 압축기는 내부 유체의 온도를 높게 상승시키기 때문에 온도 변화에 따라 공기 특성이 변화한다. 따라서, 본 연구에서는 압축성 유동을 계산하기 위해 밀도를 상수로 표현하지 않고, 높은 온도로 상승한 내부 유체의 밀도 변화를 고려하기 위해 이상기체 방정식을 함께 계산하였다. 또한, 이상 기체 방정식을 계산하기 위해 유체의 온도 변화를 함께 계산하였다.
압축기 입구에서는 일반적으로 미세한 크기의 음압(Negative Pressure)이 발생한다. 따라서, 정상 작동으로 가정한 압축기의 입구 압력(99.94 kPa)을 경계조건으로 사용하였고, 시험적으로 측정된 작동 유량인 54 g/s를 출구 경계조건으로 활용하였다. 본 압축기의 실제 작동 조건인 115,000 RPM을 대상으로 연구는 수행되었다. 시험 조건과 동일한 경계조건 설정을 위해
Fig. 2의 입구 경계면에 압력과 출구 경계면에 질량유량을 적용하였으며, 회전운동을 고려하기 위해 별도의 회전 유동장(Rotational Domain)을 생성하여 작동 회전속도를 부여하였다. 유동장 내 유체의 복잡한 난류 특성을 모사하기 위해
k -
ω SST 난류 모델을 사용하여 유체 거동을 모사하였다.
k -
ω SST 모델은 터보 기계 수치 해석에 주로 사용되며, 국소 와류 예측에 장점이 있다. 따라서, 벽면 박리와 복잡한 유동 예측에 적합하여, 정상상태 기반 공력 소음 유발 유동 특성을 효율적으로 분석하기 위해 사용되었다. 연구에서 적용된 실제 원심 압축기의 시험 및 작동 조건과 수치해 도출을 위해 사용된 모델을
Table 1으로 정리하였다.
Table 1Boundary conditions and physical properties of centrifugal compressor
Table 1
|
Inlet |
Total pressure |
99.94 kPa |
|
Total temperature |
291.5 K |
|
Outlet |
Mass flow rate |
54 g/s |
|
Rotational speed |
115,000 RPM |
|
Turbulence model |
k-ω SST |
|
Interface type |
Frozen rotor |
3. 결과 및 고찰
본 연구에 사용된 원심 압축기는 최대 약 115,000 RPM 이상의 속도로 회전하는 초고속 터보 기계이다. 작동 회전속도에서는 1.2 이상의 압축비를 가지며, 고속의 운동에너지를 활용하여 유체의 압력을 크게 상승시킨다. 하지만, 이때 발생하는 높은 운동에너지로 인하여 불안정한 공력 특성 및 소음을 야기한다는 본질적인 문제가 있다. 따라서, 소음 문제를 효율적으로 예측하고 개선이 가능하도록 정상상태 전산수치해석 결과를 기반으로 내부 유동의 불안정성 및 소음을 유발할 수 있는 유동 인자에 대해 분석하였다.
3.1 볼류트 하우징
압축기 휠 주위 볼류트와 입출구 유동해 분포를
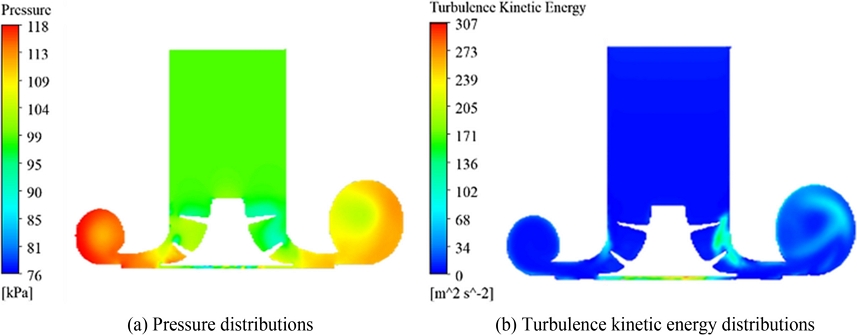
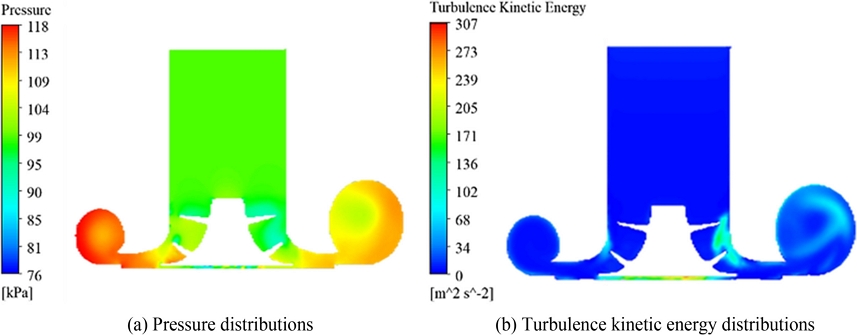
Fig. 3으로 도시하였다. 볼류트는 압축기 휠로 인해 압축된 유체 면적을 증가시켜, 내부 유체의 속도 저하와 동시에 압력을 높이는 효과가 있다. 따라서, 압축기 내부 유체의 이동으로 인해 발생하는 압력 손실을 완화한다.
Fig. 3(a)와 같이 대기압에 가까운 압축기 입구 압력은 압축부를 통과하면서 급격히 상승하며, 볼류트를 통해 압력 손실을 완화한다. 고압의 유체는 회전부를 지나 볼류트 벽면을 따라 발생하며, 중심부는 비교적 압력이 낮게 계산되었다.
Fig. 3(b)는 난류 운동에너지 분포로 좁은 간극을 지나는 구간에서 국소적으로 높게 계산되었다. 특히, 압축기 휠 배면에서 매우 높게 계산되었으며, 이는 급격하게 유동 특성이 변화하는 구간으로 극변하는 국소적 유동 현상을 수치적으로 모사할 경우에 중요하게 고려가 필요한 영역이다. 또한, 볼류트에서는 큰 와류 형태의 큰 난류 운동에너지가 생성되었다. 이러한 난류로 인한 출구 압력 손실은 미소할 것으로 판단된다. 하지만, 높은 난류 에너지로 인하여 고주파 소음에 큰 영향을 미칠 수 있다. 이는 소음 측면에서는 쉽게 소산되는 현상이나, 복잡한 난류에 의해 발생하는 유동 손실을 최소화하기 위해서는 검토가 요구된다.
Fig. 3Sectional flow characteristics of the volute housing in centrifugal compressor
3.2 압축기 회전부
고속으로 회전하는 압축기 휠의 급격한 압력 변화를 관측하기 위해 표면 압력 분포를
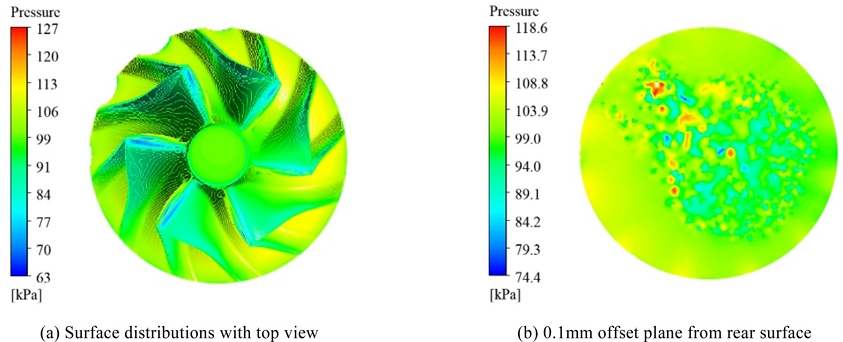
Fig. 4에 나타내었다.
Fig. 4Pressure distributions on the compressor wheel
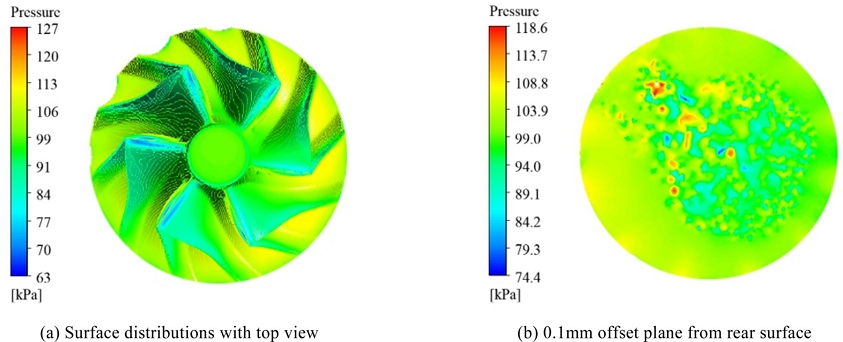
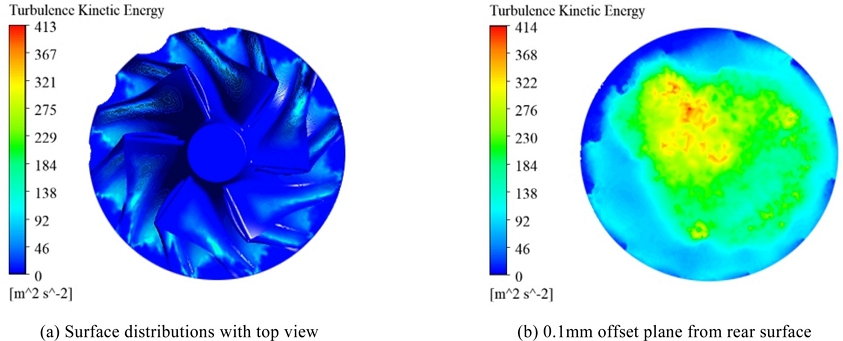
압축기 휠의 상부(
Fig. 4(a))에는 입구를 통해 유입되는 유체의 저압 특성이 관측되었고, 비교적 균일한 압력 분포를 보였다. 원심 압축기 블레이드를 통과하며, 블레이드 방향을 따라 유체의 압력은 증가하였다. 또한, 대칭형 형상으로 인해 전체적으로 균일한 압력 분포가 발생하였다. 하지만, 배면 특성은 상부와 상이하게 관측되었다. 압축기 하우징 배면의 모든 위치에서 유사한 공력 특성이 발생하였기 때문에 공력 특성을 극명하게 비교하기 위해 압축기 휠로부터 0.1 mm 이격된 거리에서 압력 특성을 비교하였다.
Figs. 4(b)으로 도시된 압축기 휠의 배면 압력은 4(a)의 상부에 비해 높게 계산되었다. 또한, 밸런싱 컷팅된 압축기 휠 인근(좌측 상단)에서 국소적으로 높은 압력 분포 및 비대칭 특성이 관측되었다. 따라서, 기계적 안정성 확보를 위해 수행된 밸런싱 컷팅은 공기역학적 불안정성에 기여할 수 있다는 것을 수치해석적 해에 기반하여 확인하였으며, 이는 고속으로 연속 회전하는 압축기 휠에서 불안정한 주파수 특성을 발생시킬 수 있다고 사료된다. 이러한 압력 분포 특성은 급격한 유체의 이동을 야기하여 유동 유발 소음에 영향을 미친다. 특히 높은 압력 구배가 발생하는 위치는 주요 소음원이 되며, 유체의 불안정한 유동 현상은 와류 발생에도 기여하게 된다. 고주파 소음의 요인이 되는 와류는 높은 압력차로 인해 불규칙한 유체가 급격히 이동하거나, 압축기 내부 형상적 특성에 따라서 높게 관측된다.
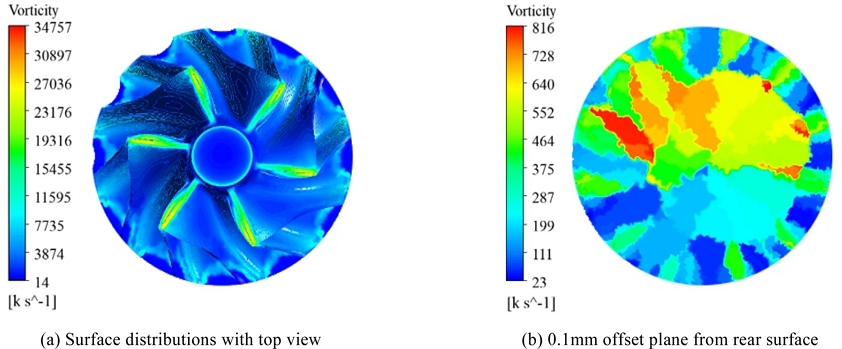
Fig. 5는 같은 영역에서의 와도 분포를 나타낸다. 압축기 휠 상부와 입구 유동이 만나는 곳에서 국소적으로 약 3.48 × 10
5s-1로 가장 높은 와도가 발생하였다. 이는 비교적 안정적인 압축기 입구 유동이 블레이드의 회전 영향을 받은 유체와 만나는 구간으로 극심한 와도가 발생하게 된다. 이러한 입구 영역에서는 흡입(Suction) 및 유동 불안정성으로 인한 소음이 높게 발생한다. 또한, 역류(Reverse Flow) 등으로 인해 공기역학적 성능에 영향을 미칠 수 있기 때문에 성능 및 소음 등 다양한 관점에서의 유동 안정화가 필수적으로 고려되어야 한다
[15].
Fig. 5Vorticity distributions on the compressor wheel
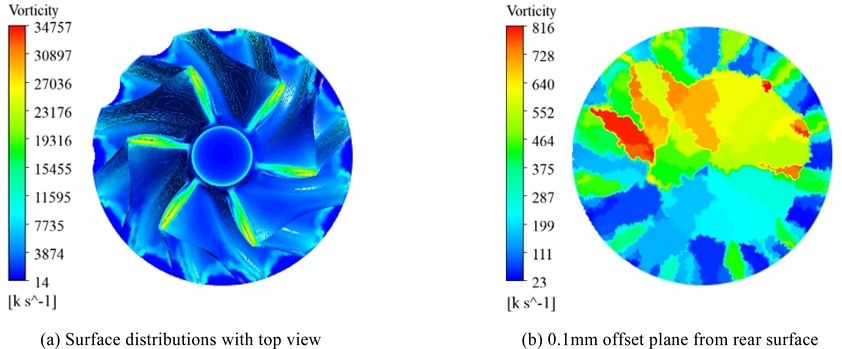
입구로 유입되는 유동과 회전 운동이 만나는 구간을 제외하고는 압축기 휠 상부 면에서는 블레이드를 통과하는 방향으로 낮은 와도가 계산되었다. 좁은 유로를 통과하는 압축기 배면에서는 압축기 휠의 배면과 이격된 거리에 비교적 높은 와도가 계산되었다. 와도는 밸런싱 컷팅된 좌측 상단 위치에서 약 8.16 × 105s-1 으로 비교적 높게 계산되었다. 따라서, 원심 압축기에서 와도는 형상적 비대칭 특성(밸런싱 컷팅)의 영향을 크게 받으며, 지배적으로는 형상 또는 기능적 특성으로 인해 급격한 유동의 변화가 발생하는 지점에서 높게 확인 가능함을 본 연구를 통해 입증하였다.
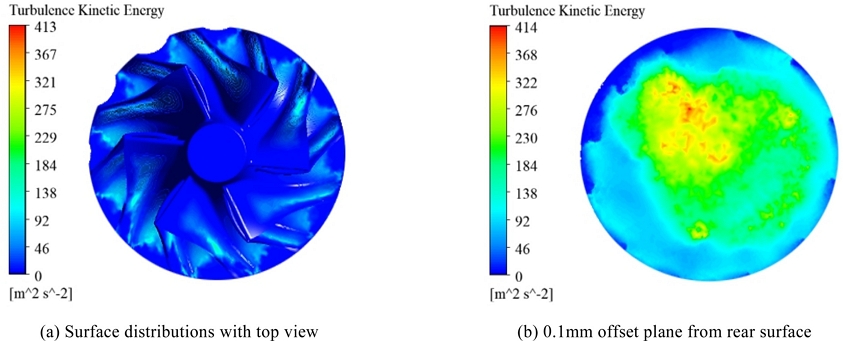
와도 특성과 다르게 난류 운동에너지는 압축기 휠 상부 분포에 있어서 위치별 큰 차이가 발생하지는 않았다(
Fig. 6(a)). 또한, 블레이드 상부에 비해서 하우징으로 유출되는 출구부에 비교적 높은 난류 운동에너지가 계산되었다. 압축기 휠 배면에서는 상부에 비해 위치별 난류 운동에너지 분포가 상이하게 나타났다. 가장 높은 난류 운동에너지 또한 밸런싱 컷팅부 인접 위치에서 계산되었다. 이는 비대칭 형상이 압축기 인근 난류 운동에너지 발생에 영향을 미친다고 판단된다. 난류 운동에너지의 경우 압축기 배면에서부터 이격된 위치에서의 압축기 휠 표면 분포를
Fig. 6(b)에 도시하였다. 해당 위치에서 난류 운동에너지는 최대 414.32
m2s–2로 계산되었다. 컷팅에 의한 비대칭 형상은 압축기 배면 전반의 난류 운동에너지 분포에 악영향을 미쳤다. 본 유동 인자는 복잡한 유동 특성을 발생시켜 고주파 소음에 영향을 미칠 수 있으나, 고주파 소음의 특성상 이격된 거리에 위치한 청취자에게는 영향이 미미할 것으로 예측된다.
Fig. 6Turbulence kinetic energy distributions on the compressor wheel
3.3 배면 유동 특성
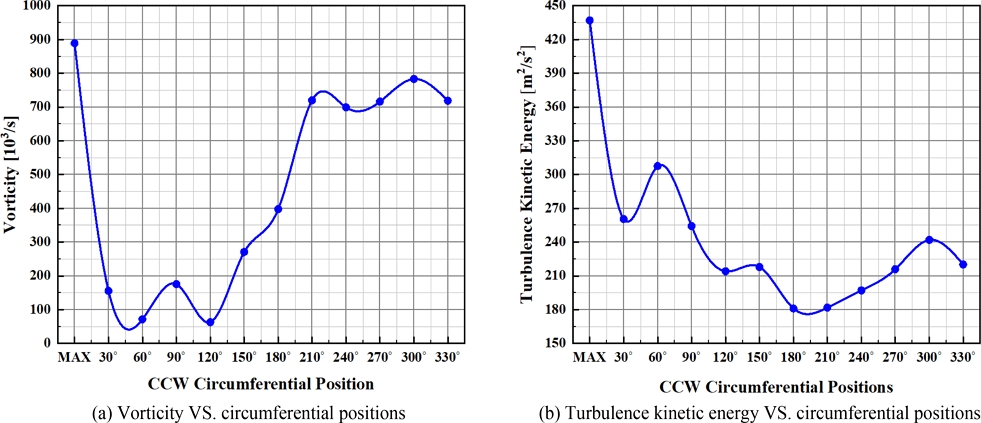
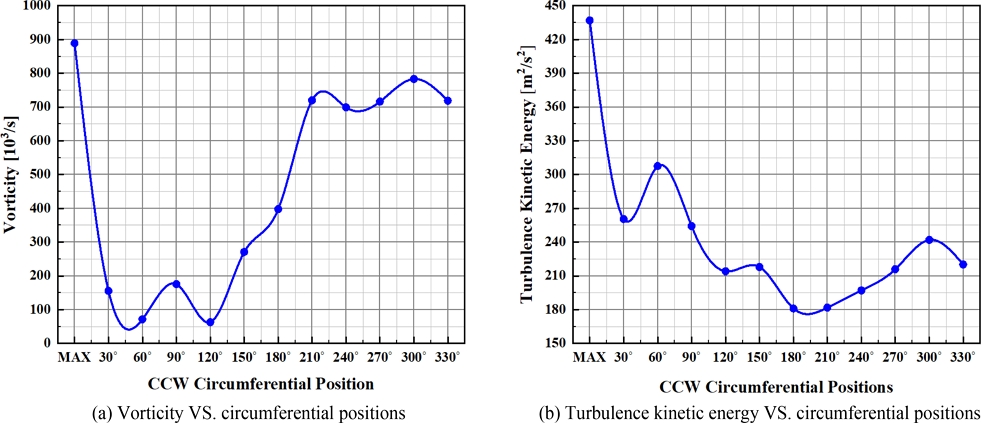
Fig. 7은 각각 압축기 배면에서 계산된 와도와 난류 운동에너지이다. 최대 와도를 기준으로 반시계 방향 30도씩 위치에 대한 와도 분포를
Fig. 7(a)로 정리하였다. 와도는 형상적으로 비대칭 특성을 지닌 밸런싱 컷팅 인근에서 가장 높은 수치로 계산되었으며, 압축기 회전 방향으로 점차 감소하였다. 이는 압축기 하우징을 통과하여 외부로 유출되는 출구 방향인 200도 인근에서 다시 높은 값으로 복귀 후 점진적으로 증가하는 경향을 보였다. 와도가 급감하는 영역은 출구 방향으로 송출되는 지배적인 유동으로 인하여 와도가 발달하지 않고 소멸되기 때문에 낮은 와도가 계산되었다. 하지만, 최대 와도가 계산되는 밸런싱 컷팅부 인근으로 근접할수록 와도 분포가 순차적으로 높아지는 형태를 보였다. 밸런싱 컷팅으로 인한 높은 와도 발생으로 휠 인근 불안정성 및 고주파 소음에 영향을 미칠 수 있으며, 압축기 출구 방향 와류 특성으로 소음에 직접적인 영향을 미칠 수 있다. 따라서, 공기역학적 특성 및 소음 측면에서 밸런싱 컷팅 및 출구 유동 안정화가 고려될 필요가 있다.
Fig. 7(b)는 동일 위치에서의 난류 운동에너지 분포를 정리하였다. 난류 운동에너지 분포는 와도 분포와 유사하게 최대 와도 지점을 지나며 급감하였다. 하지만, 이후 높은 값으로 복귀하는 와도 특성과 다르게 연속적으로 낮은 난류 운동에너지 분포가 계산되었다. 하우징으로 폐쇄되는 유동 영역인 300도 인근에서 발생하는 복잡한 유동현상으로 인해 와도가 높게 발생하지만, 하우징 형상으로 인해 난류 운동에너지는 오히려 저감되었다.
Fig. 7Turbulence flow characteristics on rear surface of the compressor wheel
4. 결론
본 연구에서는 수십만 RPM 이상의 초고속으로 회전하는 원심 압축기의 정상상태 공력 해석 데이터를 기반으로 소음을 유발할 수 있는 공기역학적 특정 유동 인자에 대해 분석하였다. 정상해 기반의 소음 분석은 공기역학적 비정상 항들을 소거하기 때문에 비정상 특성이 반영되지 않는다. 하지만, 원심 압축기의 소음을 직접적으로 계산하는 일은 수많은 자원과 비용이 소모되기 때문에 효율적인 초기 연구 및 제품 개발을 위하여 정상 상태 기반 예측 방법론을 제안하였으며, 그 결론을 다음과 같이 정리하였다.
(1)초고속 원심 압축기의 공기역학적 성능과 유동 유발 소음을 수치적으로 연구하기 위해 K(社)의 중형 차량용 원심 압축기를 사용하였다. 소음을 예측하기 위해 회전하는 유동장과 비회전 유동장을 분리하여 온도 변화를 고려한 지배 방정식을 계산하였다. 54 g/s의 출구 유량을 가지는 원심 압축기 작동 조건인 115,000 RPM을 대상으로 연구를 수행하였으며, 해당 조건에서의 압축기 내부 유동 불안정성 및 소음 유발 인자를 분석하였다.
(2) 압축 유체의 면적을 증가시켜 속도 저하와 동시에 압력을 높이는 효과를 가진 볼류트는 압축기 내부 압력 손실을 완화시킨다. 내부 유체가 이동하는 면적이 급격히 감소하는 경우 난류 운동에너지는 국소적으로 증가하며, 불안정한 유동 특성을 보였다. 볼류트에서 발생한 이러한 특성은 출구의 높은 압력차에 비해 약한 크기의 소음을 발생시키며, 쉽게 소산되는 고주파 소음에 기여하기 때문에 전체 소음에 미치는 영향은 미미할 것으로 보인다.
(3) 공기역학적 소음에 크게 기여하는 급격한 압력의 변화는 압축기 전반부에 걸쳐 확인되었다. 특히, 압축기 출구와 배면 인근에서 극대화되는 경향을 보였다. 압축기 휠 상부와 입구 유동이 만나는 지점에서 매우 높은 크기의 와도가 발생하였고, 이는 입구 흡입 및 유동 불안정성에 의한 소음과 역류 등을 야기하였다. 와도는 형상적 비대칭성이 극명한 밸런싱 컷팅 주위에도 비교적 높은 수치로 계산되어 컷팅으로 인한 고주파 소음이 발생함을 예상할 수 있었다.
(4) 난류 운동에너지는 압축기 휠 상부면 분포에 있어서 와도 특성과 상이하게 위치별 큰 차이가 발생하지 않았다. 압축기 휠의 운동에너지를 받은 출구부에서 비교적 높은 값이 계산되었으며, 형상적 변화가 극심한 밸런싱 컷팅부 인근에서 최대값이 확인되었다. 고속으로 회전하는 압축기 휠의 형상적 비대칭 특성은 난류 운동에너지에 직접적인 영향을 미쳐 유동 불안정성 및 고주파 소음에 기여함을 알 수 있다. 고주파 소음은 소음의 강도가 약해 특정 거리가 이격된 청취자에게 미치는 영향은 미미하기 때문에 쉽게 소산됨을 예측할 수 있었다.
(5) 복잡한 유동이 발생하는 압축기 휠에 밀접한 영역과는 다르게 출구 인근에서는 지배적인 유동으로 인해 와류 생성이 낮게 계산되었다. 이는 출구 이후 송출되는 곳에서는 미미하게 높은 분포이나, 밸런싱 컷팅 인근에서 최대값을 보였다. 난류 운동에너지 분포 또한 와도와 유사하게 밸런스 컷팅 지점 인근에서 높게 계산되었으며, 이후 급감하는 경향이 확인되었다. 따라서, 와도 및 운동에너지 등 고주파 소음에 기여하는 유동 인자는 압축기 하우징 및 출입구 보다는 국소적 비대칭 형상에서 발생하며 높은 회전 속도로 운동하는 밸런싱 컷팅 인근에서 영향을 크게 받음을 확인할 수 있었다.
ACKNOWLEDGMENTS
이 결과물은 2024년도 대구가톨릭대학교 학술연구비 지원에 의한 것임.
REFERENCES
- 1.
Shi, T., Chen, Q., Peng, X., Feng, F., Guo, Y., (2023), Multi-objective optimization of the oil-free centrifugal air compressor in hydrogen fuel cell vehicles based on grey relational analysis, International Journal of Hydrogen Energy, 48(67), 26341-26355.
10.1016/j.ijhydene.2023.03.346
- 2.
Nguyen-Schäfer, H., Kleinschmidt, R., (2012), Analysis and nonlinear rotordynamics computation of constant tone in automotive turbochargers, Proceedings of the 17th Aufladetechnische Konferenz.
- 3.
Nguyen-Schäfer, H., (2013), Aero and vibroacoustics of automotive turbochargers, Springer Science & Business Media.
10.1007/978-3-642-35070-2
- 4.
Park, H. I., Eom, S. B., Seo, J. B., Lee, S. H., (2012), Compressor BPF noise reduction for an automotive turbocharger, Proceedings of the Korean Society for Noise and Vibration Engineering Conference, 851-856.
- 5.
Jin, J., Lee, S., (2013), Effect of volute shape on performance of turbocharger, Proceedings of the Korean Society for Precision Engineering Spring Conference, 240-246.
- 6.
Tianjun, Z., Lee, G. S., (2013), Flow field characteristics of the two types of three-arcs overhung volute for an automobile turbocharger compressor, Proceedings of the Korean Society of Mechanical Engineers Autumn Conference, 4040-4044.
- 7.
Lee, I., Choi, B., (2016), Development of finite element model for predicting the axial thrust in a turbocharger, Journal of the Korean Society of Mechanical Technology, 18(3), 411-417.
10.17958/ksmt.18.3.201606.411
- 8.
Song, R., Lee, D., (2015), Study on the flow analysis in the micro gas turbine with different rotational speeds, Journal of the Society of Air-Conditioning and Refrigerating Engineers of Korea, 421-425.
- 9.
An, I., Lee, Y., (2015), CFD Analysis on efficiency improvement of a linear compressor using turbocharging, Journal of the Korean Society of Mechanical Technology, 17(1), 63-68.
10.17958/ksmt.17.1.201502.63
- 10.
Kim, G., Lee, D., (2016), A study on the flow analysis in the turbocharger turbine with different rotational speeds, Journal of the Korean Society of Mechanical Technology, 18(5), 734-739.
10.17958/ksmt.18.5.201610.734
- 11.
Xu, C., Zhou, H., Mao, Y., (2020), Analysis of vibration and noise induced by unsteady flow inside a centrifugal compressor, Aerospace Science and Technology, 107, 106286.
10.1016/j.ast.2020.106286
- 12.
Semlitsch, B., Mihaescu, M., (2016), Flow phenomena leading to surge in a centrifugal compressor, Energy, 103, 572-587.
10.1016/j.energy.2016.03.032
- 13.
Liu, C., Cao, Y., Liu, Y., Zhang, W., Ming, P., Ding, S., (2019), Numerical and experimental analyses of intake silencer and its effects on turbocharger compressor performance, Journal of Advances in Mechanical Engineering, 11(3).
10.1177/1687814019826677
- 14.
Song, J. H., Lee, D. R., (2020), A study on aero-acoustics of high-speed turbomachinery for different rotational speeds, Journal of the Korean Society for Precision Engineering, 37(12), 897-904.
10.7736/JKSPE.020.072
- 15.
Song, J. H., (2022), Aeroacoustic optimization for centrifugal compressor using inlet groove, M.Sc. Thesis, Sungkyunkwan University.
Biography
- Jihun Song
Research Engineer in the Rotorcraft System Analysis team, Korea Aerospace Industries (KAI). His research interest is Aeroacoustics, Aerodynamics, and Optimization for Rotorcraft and Turbo Machinery.
- Chang Ho Son
M.S. candidate in the Department of Mechanical Engineering, Graduate School of Sungkyunkwan University. His research interest is Urban Air Mobility, Electric Vehicle, and Aerodynamics.
- Dong-Ryul Lee
Professor in the Department of Mechanical Engineering, Daegu Catholic University. His research interest is Heat Transfer, Fluid Engineering, Electric Vehicle, and Advanced Air Mobility.