ABSTRACT
The rapid growth of semiconductor and display manufacturing highlights the demand for fast, precise motion stages. Advanced systems such as lithography and bio-stages require accuracy at the μm and nm levels, but linear motor stages face challenges from disturbances, model uncertainties, and measurement noise. Disturbances and uncertainties cause deviations from models, while noise limits control gains and performance. Disturbance Observers (DOBs) enhance performance by compensating for these effects using input–output data and a nominal inverse model. However, widening the disturbance estimation bandwidth increases noise sensitivity. Conversely, the Kalman Filter (KF) estimates system states from noisy measurements, reducing noise in position feedback, but it does not treat disturbances as states, limiting compensation. To address this, we propose an Augmented Kalman Filter (AKF)–based position control for linear motor stages. The system was modeled and identified through frequency response analysis, and DOB and AKF were implemented with a PIV servo filter. Experimental validation showed reduced following error, jitter, and control effort, demonstrating the improved control performance of the AKF approach over conventional methods.
-
KEYWORDS: Linear motor motion stage, Model uncertainty, Measurement noise, PIV controller, Augmented Kalman filter, Disturbance observer, Kalman filter
-
KEYWORDS: 선형 모터 모션 스테이지, 모델 불확실성, 측정 잡음, PIV 제어기, 증강 칼만 필터, 외란 관측기, 칼만 필터
NOMENCLATURE
Cut-off Frequency of Disturbance Estimation Filter
Augmented System, Input and Output Matrix
Disturbance and Estimated Disturbance
Actual and Nominal Model of the Motor
Acceleration Feedforward Gain
Integral and Proportional Gain
Velocity Feedforward Gain
Estimation Error and Process Noise Covariance
Measurement Noise Covariance
Control Effort and Servo Out
Displacement and Velocity of the Mover
Estimated Displacement and Velocity of the Mover
1. 서론
최근 반도체 및 디스플레이 제조 산업 성장에 따라서 초고속, 초정밀 모션 스테이지의 중요성이 부각되고 있다
[1-
6]. 특히, 반도체 노광 장비 및 바이오 스테이지와 같은 첨단 장비는 μm 및 nm 단위의 정밀도가 요구된다.
정밀 위치 제어 성능 향상을 위해 제어 이득을 높이는 것이 일반적이지만 외란, 모델 불확실성 그리고 측정 잡음 등으로 인해 단순히 이득을 높이는 것에 한계가 있다
[7]. 외란 및 모델 불확실성으로 시스템이 수학 모델에서 벗어나고, 측정 잡음으로 PIV (Proportional-integral-velocity) 제어 이득을 충분히 높이지 못해 정밀 제어 성능 향상에 한계가 존재한다.
외란 관측기(Disturbance Observer, DOB)는 입력과 출력 정보 그리고 공칭 역 모델을 이용해 외란과 모델 불확실성을 보상하고 제어 성능을 향상시킨다
[8-
11]. DOB는 외란 추정 필터의 대역폭을 넓혀 외란 억제 성능을 향상시키지만 잡음 민감도도 증가시킨다. 특히 입력 신호에 고주파 잡음이 포함될 경우, 잡음이 증폭되어 전체 시스템의 안정성과 성능이 저하될 우려가 있다.
칼만 필터(Kalman Filter, KF)는 잡음이 포함된 측정 신호와 수학 모델을 기반으로 시스템 상태를 추정하고 위치 피드백에 사용하여 잡음의 영향을 줄인다. KF는 외란을 상태 변수로 고려하지 않기 때문에 외란과 모델 불확실성을 직접적으로 보상할 수 없으므로, 불확실성이 존재하는 환경에서 강건 제어 성능 확보에 한계가 있다
[12-
14].
이 논문에서는 선형 모터 모션 스테이지의 위치 제어 성능 향상을 위해 증강 칼만 필터(Augmented Kalman Filter, AKF) 기반 위치 제어를 연구하였다. 선형 모터 모션 스테이지를 모델링하고 주파수 응답을 측정하여 공칭 모델을 식별했다. 식별한 공칭 모델을 기반으로 선형 모터 모션 스테이지 위치 제어를 위한 DOB와 AKF를 설계했다. DOB와 AKF를 각각 PIV 서보 필터와 함께 적용하고 추종 오차, 제어 노력, 지터 그리고 민감도 함수를 측정해 위치 제어 성능을 검증했다.
2. 선형 모터 모션 스테이지
2.1 선형 모터 모션 스테이지 구성
선형 모터 모션 스테이지는
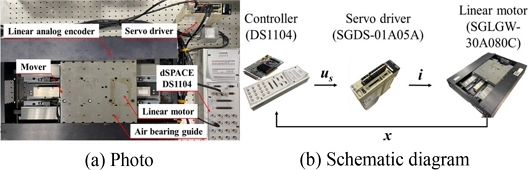
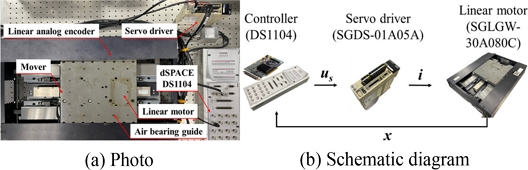
Fig. 1과 같이 공심형 선형 모터(Yaskawa, SGDS-30A080C), 서보 드라이버(Yaskawa, SGDS-01A05A), 선형 아날로그 엔코더(GSI, Mercury 2) 그리고 제어기(dSPACE, DS-1104)로 구성된다. 선형 모터 모션 스테이지는 최대 100 mm의 스트로크, 1 μm의 분해능을 가진다.
Fig. 1Experimental setup for linear motor motion stage
2.2 선형 모터 모션 스테이지의 공칭 모델 식별
선형 모터 모션 스테이지의 질량만을 고려한 운동 방정식은
식(1)과 같다. 여기서
us,
m0,
KF,
x는 각각 서보 출력, 공칭 질량, 모터 추력 계수 그리고 이동자 변위이다.
서보 출력에서 이동자 변위로의 전달함수 즉, 공칭 모델 전달함수 (
Gn(
s))는
식(2)와 같다.
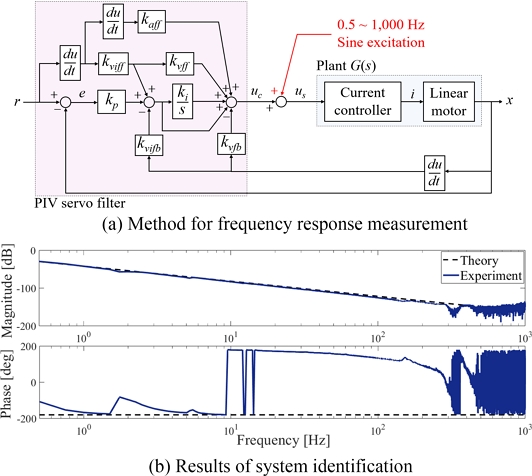
Fig. 2(a)와 같이 제어 노력(
uc)에 정현파 가진 신호를 인가하고 서보 출력(
us)에서 이동자 변위(
x)로의 주파수 응답을 측정하고 이론 값과 비교하여
Fig. 2(b)에 나타냈다. 31.5 mA 진폭의 정현파 가진 신호를 제어 노력(
uc)에 더해 0.5부터 1000 Hz까지 0.25 Hz씩 증가시켰다. 측정 주파수 응답으로부터 식별한 공칭 질량은 2.579 kg이다. 여기서
e,
KP,
KI,
Kvifb,
Kvfb,
Kvff,
Kviff,
Kaff는 각각 오차와 비례, 적분, 속도 궤환, 속도 그리고 가속도 전향 제어 이득이다.
Fig. 2Frequency response measurement of a linear motor motion system

3. DOB와 AKF
3.1 DOB 설계
외란과 모델 불확실성을 보상하기 위해
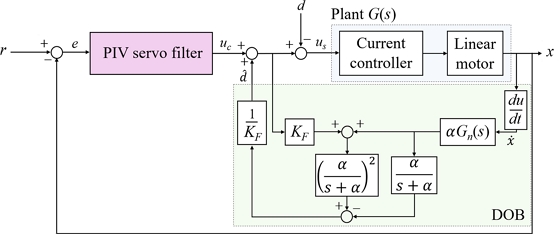
Fig. 3과 같이 공칭 역 모델과 2차 외란 추정 필터로 구성된 DOB를 모션 제어 시스템에 추가했다
[15,
16]. 여기서
G(
s),
r,
d,
d^,
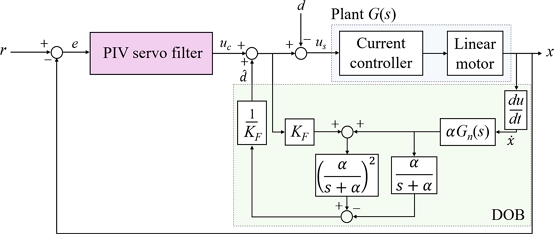
α는 각각 모터의 실제 모델, 위치 명령, 외란, 추정 외란, 외란 추정 필터 절점 주파수이다. 모션 제어 시스템의 외란과 모델 불확실성은 선형 모터의 속도와 제어 노력을 입력으로 하는 DOB를 통해 추정되고 제어 노력에 더해 그 영향을 보상한다.
Fig. 3Linear motor motion system with PIV servo filter and DOB
3.2 AKF 설계
외란, 모델 불확실성을 보상하고 측정 잡음의 영향을 줄여주기 위해
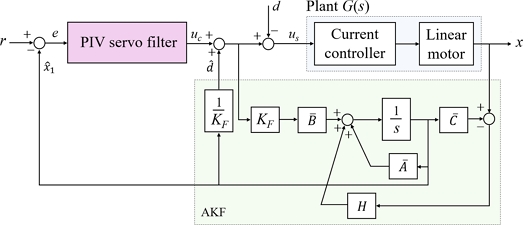
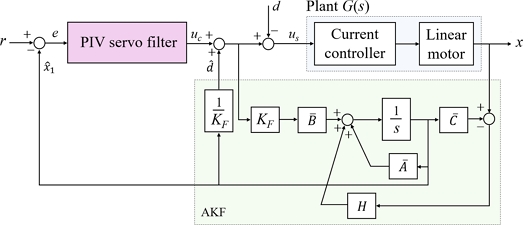
Fig. 4와 같이 외란과 상태를 동시에 추정하는 AKF를 모션 제어 시스템에 추가했다. AKF는 측정 변위, 오차의 공분산 그리고 최적 칼만 이득으로 구성했다. AKF를 통해 추정한 변위
x^1와 외란
d^를 위치 피드백과 외란 보상에 사용해 잡음의 영향을 최소화한다. 선형 모터의 운동 방정식
식(1)을 상태 공간으로 나타내면
식(3)과 같다. 여기서
x1,
x2는 각각 이동자 변위 그리고 속도이고
y는 시스템 출력인 이동자 변위이다.
Fig. 4Linear motor motion system with PIV servo filter and AKF
AKF로 외란과 불확실성을 보상하기 위해
식(3)을 외란이 포함된 상태 방정식인
식(4)와 같이 구성했다
[17,
18]. 여기서
A-,
B-,
C-,
X-는 각각 시스템, 입력, 출력 증강 행렬 그리고 외란이 포함된 증강 상태 변수 행렬이다.
증강 상태 행렬을 추정하기 위한 연속시간 증강 칼만 필터는
식(5)와 같은 관측기 구조를 가진다. 여기서
H는 최적 칼만 이득 행렬이다.
식(6)의 비용함수
J를 최소화하기 위해
식(7)의 연속시간 Riccati 방정식으로 추정 오차 공분산 행렬
P를 계산하고
식(8)의 최적 칼만 이득 행렬을 도출한다. 여기서
Q,
R은 각각 프로세스 잡음과 측정 잡음의 공분산 행렬이다
[19,
20].
AKF를 통해 실시간으로 추정된 외란(
d^)과 변위 (
x^1)를
Fig. 4와 같이 위치 피드백과 외란 보상에 사용해 외란과 측정 잡음의 영향을 동시에 줄일 수 있다
[21].
4. DOB와 AKF의 성능 검증
4.1 모션 프로파일
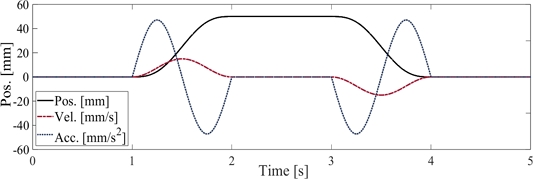
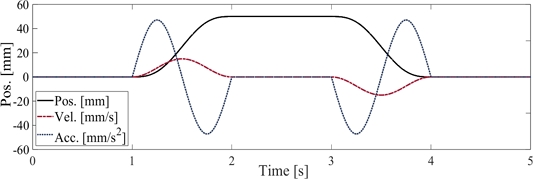
Fig. 5와 같은 100 mm/s 최대 속도와 314 mm/s
2 최대 가속도로 50 mm를 왕복하는 모션 프로파일로 위치 제어기 성능을 평가했다.
Fig. 5Motion profile to evaluate the control performance of DOB and AKF
4.2 DOB와 AKF의 위치 제어 성능 검증
DOB와 AKF를 PIV 서보 필터와 각각 함께 적용했을 때 추종 오차, 제어 노력 그리고 지터를
Fig. 6과
Table 3에 나타냈다. PIV 서보 필터 단독 적용 대비 DOB를 함께 적용했을 때 위치 오차와 제어 노력이 각각 19%, 54% 감소했으나, DOB가 측정 잡음을 증폭하여 지터가 37% 증가했다. AKF를 함께 적용한 경우 측정 잡음 영향이 줄어든 추정 변위를 위치 피드백에 사용하여 위치 오차, 지터, 제어 노력이 각각 32%, 45%, 66% 감소했다.
Fig. 6Comparison of position errors, control efforts and jitters W/O mass: PIV and PIV W/T DOB or AKF
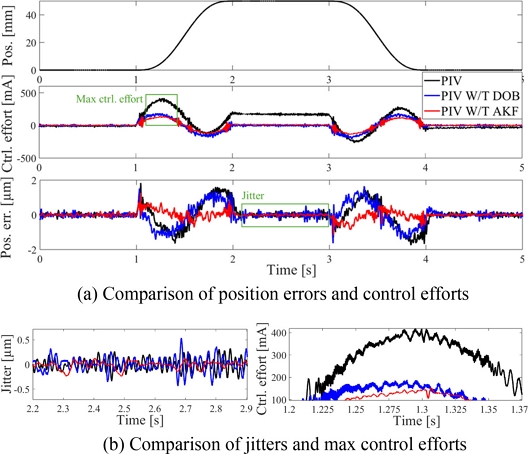
Table 3Comparison of position errors, control efforts and jitters W/T mass: PIV and PIV W/T DOB or AKF
Table 3
|
PIV |
PIV W/T DOB |
PIV W/T AKF |
|
Position error [µm] |
1.85 |
1.50 |
1.24 |
|
Control effort [mA] |
417 |
188 |
142 |
|
Jitter [µm] |
0.22 |
0.35 |
0.12 |
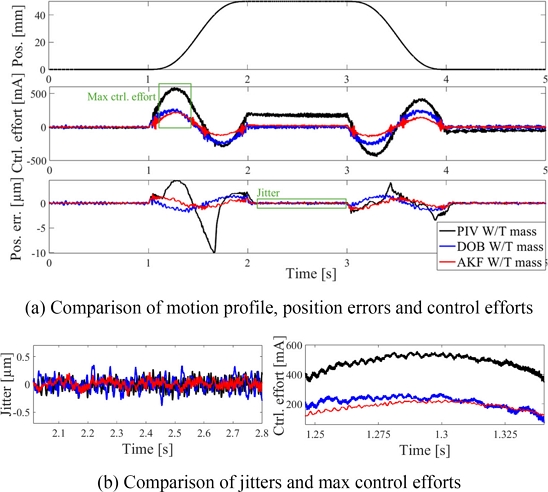
Fig. 7과 같이 선형 모터 이동자에 5 kg 질량을 추가하고 동일한 실험을 수행하여 그 결과를
Fig. 8과
Table 4에 나타냈다. PIV 서보 필터 단독 사용시 공칭 모델 변화 전 대비 위치 오차와 제어 노력이 각각 최대 82%, 28% 증가했다. DOB를 함께 적용한 경우 공칭 모델 변화에 대응하여 PIV 서보 필터만 적용했을 때 대비 위치 오차와 제어 노력이 82%, 53% 감소했으며 AKF를 함께 적용했을 때는 위치 오차와 제어 노력이 각각 83%, 63% 감소했다.
Fig. 7Linear motor motion stage mover with 5 kg mass

Fig. 8Comparison of position errors, control efforts and jitters W/T mass: PIV and PIV W/T DOB or AKF
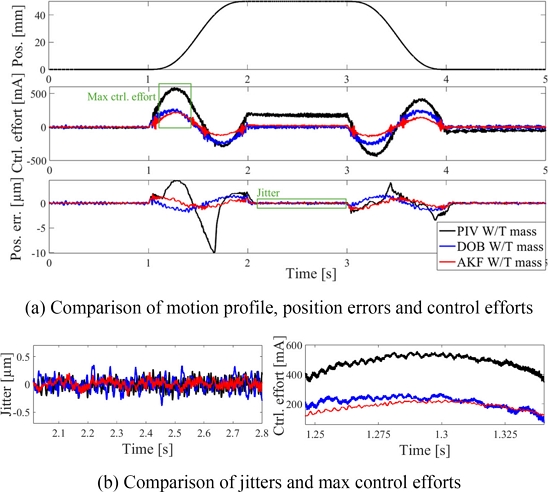
Table 4Comparison of position errors, control efforts and jitters W/T mass: PIV and PIV W/T DOB or AKF W/T DOB PIV W/T AKF
Table 4
|
PIV |
PIV W/T DOB |
PIV W/T AKF |
|
Position error [µm] |
10.1 |
1.78 |
1.66 |
|
Control effort [mA] |
586 |
273 |
217 |
|
Jitter [µm] |
0.22 |
0.34 |
0.13 |
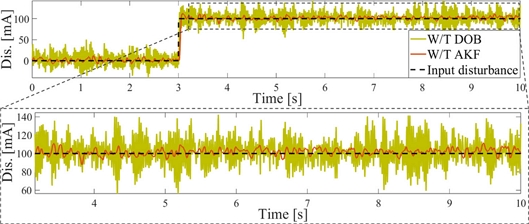
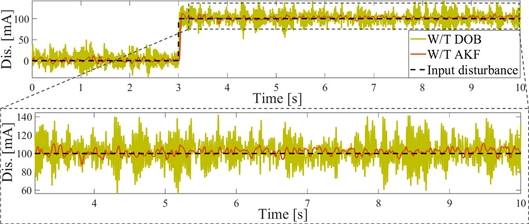
DOB와 AKF의 외란 추정 성능을 평가하기 위해 100 mA 계단 외란을 입력하고 추정 외란을 비교하여
Fig. 9에 나타냈다. DOB 추정 외란 대비 AKF 추정 외란에서 고주파 잡음의 영향이 21% 줄었다.
Fig. 9Comparison of estimated disturbance with step disturbance using DOB or AKF
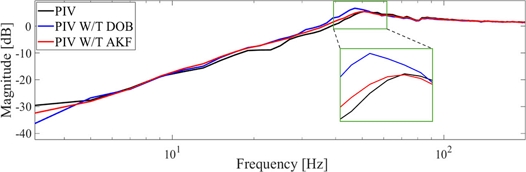
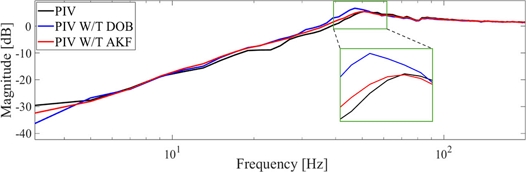
DOB와 AKF의 외란 억제 성능을 평가하기 위해 정현파 가진 신호를 0.5부터 300 H까지 2 Hz씩 증가시키며 위치 명령에 인가하여 정현파 위치 명령에 대한 이동자 변위의 주파수 응답을 측정하고 민감도 함수를 계산해
Fig. 10에 나타냈다. DOB를 적용한 경우 PIV 단독 적용 대비 저주파 영역에서 민감도를 낮추었지만 민감도 최대값이 증가했다. AKF를 함께 적용한 경우 저주파 영역에서 민감도 함수가 감소하면서도 민감도 최대값이 증가하지 않았다.
Fig. 10Comparison of sensitivity function: PIV and PIV W/T DOB or AKF
5. 결론
이 논문에서는 선형 모터 모션 스테이지의 위치 제어 성능 향상을 위해 증강 칼만 필터 기반 위치 제어를 연구하였다. 선형 모터 모션 스테이지를 모델링하고 측정 주파수 응답과 비교해 식별하였다. 식별한 공칭 모델을 기반으로 DOB와 AKF를 설계하고 모션 제어 시스템에 추가했다. DOB와 PIV 서보 필터를 함께 적용하여 외란과 모델 불확실성을 보상해 위치 제어 성능이 향상되었으나, 측정 잡음이 증폭되어 지터 성능이 저하되었다. AKF를 PIV 서보 필터와 함께 적용하면 외란과 모델 불확실성의 영향을 줄이는 동시에 측정 잡음의 영향을 억제해 위치 제어 성능과 지터 성능이 모두 향상되었다. AKF 기반 위치 제어는 정밀 제어와 외란 억제가 요구되는 반도체 및 디스플레이 제조 장비, 초정밀 가공 시스템 등에 적용되어 장비 구조의 유연성, 부하 변동성 그리고 외부 진동 환경이 복합적으로 영향을 미치는 산업 현장에서 강인한 위치 제어 성능을 제공할 수 있다.
ACKNOWLEDGMENTS
이 연구는 산업통상자원부(한국 산업 기술 평가 관리원) 산업기술혁신사업(2021년도 소재부품기술개발사업)의 지원으로 수행되었음(No. 20017202).
REFERENCES
- 1.
Chen, Z., Yao, B., Wang, Q., (2014), µ-Synthesis based adaptive robust control of linear motor driven stages with high-frequency dynamics: A case study, IEEE/ASME Transactions on Mechatronics, 20(3), 1482-1490.
10.1109/TMECH.2014.2369454
- 2.
Hwang, K., Jeong, J., Ahn, H.-J., (2017), Input shaping methods for a linear motor motion stage with a passive RFC (Reaction Force Compensation) mechanism, Journal of the Korean Society for Precision Engineering, 34(12), 897-902.
10.7736/KSPE.2017.34.12.897
- 3.
Yang, K. H., Ahn, H.-J., (2024), Customized current control of a linear motor motion stage, Journal of the Korean Society for Precision Engineering, 41(11), 875-880.
10.7736/JKSPE.024.085
- 4.
Yang, K. H., Ahn, H.-J., (2024), Fuzzy neural network control for a reaction force compensation linear motor motion stage, International Journal of Precision Engineering and Manufacturing-Smart Technology, 2(2), 109-114.
10.57062/ijpem-st.2024.00038
- 5.
Shin, J. M., Ahn, H.-J., (2025), Vibration issues in precision equipment: Challenges and mitigation strategies of pneumatic vibration isolators, International Journal of Precision Engineering and Manufacturing, 26(10), 2223-2242
10.1007/s12541-025-01327-1
- 6.
Kim, K. H., Song, J. W., Choi, M. H., Ahn, H.-J., (2025), Smart tuned mass damper with adjustable stiffness and damping, Transactions of the Korean Society of Mechanical Engineers A, 49(6), 423-428.
10.3795/KSME-A.2025.49.6.423
- 7.
Cho, J., Choi, D., Ahn, H.-J., (2011), Mechanism and control of reaction force compensation of XY linear motion stage system, Transactions of the Korean Society of Mechanical Engineers A, 35(6), 599-607.
10.3795/KSME-A.2011.35.6.599
- 8.
Tena, D., Peñarrocha-Alós, I., Sanchis, R. (2022), Performance, robustness and noise amplification trade-offs in Disturbance Observer Control design, European Journal of Control, 65, 100630.
10.1016/j.ejcon.2022.100630
- 9.
Joo, Y., (2024), Performance recovery and stability analysis of disturbance observer under unmodeled dynamics, Sensors, 24(23), 7850.
10.3390/s24237850
- 10.
Yoo, S. J., Ahn, H.-J., (2020), Software-based integral product architecture for modular motion control system of a RFC linear motor motion stage: Model-based DOB for residual vibration suppression, International Journal of Precision Engineering and Manufacturing, 21(1), 203-209.
10.1007/s12541-019-00212-y
- 11.
Shin, J. M., Ahn, H.-J., (2025), Enhanced pressure control using a disturbance observer for active pneumatic vibration isolator (PVI), International Journal of Precision Engineering and Manufacturing, 26(4), 887-893.
10.1007/s12541-024-01174-6
- 12.
Jang, D., Jang, S., Kim, G., Choi, H., (2002), Trace of moving object using structured Kalman filter, Journal of KIISE: Software and Applications, 29(5), 319-325.
- 13.
Naoual, T., Djamel, O., Abderrezak, G., Messaoud, R., (2022), Advanced control with extended Kalman filter and disturbance observer, Indonesian Journal of Electrical Engineering and Computer Science, 28(1), 124-136.
10.11591/ijeecs.v28.i1.pp124-136
- 14.
Tang, J., Li, B., Chang, J., Zhang, A., (2020), Unscented Kalman-filter-based sliding mode control for an underwater gliding snake-like robot, Science China Information Sciences, 63, 1-13.
10.1007/s11432-019-1470-x
- 15.
Jeon, H., Ahn, H.-J., (2024), Model-based motion control design of a linear motor stage in frequency domain, Journal of the Korean Society for Precision Engineering, 41(1), 55-60.
10.7736/JKSPE.023.107
- 16.
Lee, K., Cha, J., Park, S., (2023), Disturbance observer-based control to guarantee a sliding mode without sliding mode control, IEEE Access, 11, 95632-95638.
10.1109/ACCESS.2023.3307738
- 17.
Kim, J., Cho, K., Choi, S., (2016), Lumped disturbance compensation using extended Kalman filter for permanent magnet linear motor system, International Journal of Control, Automation and Systems, 14(5), 1244-1253.
10.1007/s12555-014-0400-1
- 18.
Ohhira, T., Shimada, A., (2018), Movement control based on model predictive control with disturbance suppression using Kalman filter including disturbance estimation, IEEJ Journal of Industry Applications, 7(5), 387-395.
10.1541/ieejjia.7.387
- 19.
Ohhira, T., Shimada, A., Murakami, T., (2021), Variable forgetting factor-based adaptive Kalman filter with disturbance estimation considering observation noise reduction, IEEE Access, 9, 100747-100756.
10.1109/ACCESS.2021.3097342
- 20.
Liu, F., Tsiotras, P., (2024), Optimal covariance steering for continuous-time linear stochastic systems with multiplicative noise, IEEE Transactions on Automatic Control, 69(10), 7247-7254.
10.1109/TAC.2024.3402059
- 21.
Shimada, A., Yongyai, C., (2009), Motion control of inverted pendulum robots using a kalman filter based disturbance observer, SICE Journal of Control, Measurement, and System Integration, 2(1), 50-55.
10.9746/jcmsi.2.50
Biography
- Keun-Ho Kim
B.Sc. candidate in the School of Mechanical Engineering, Soongsil University. His research interest is precision motion control of a linear motor motion stage.
- Hyeong-Joon Ahn
Received his B.S., M.S. degrees from Department of Mechanical Design & Production Engineering, Seoul National University and his Ph.D. from the School of Mechanical and Aerospace Engineer-ing, Seoul National University. He joined Soongsil University in 2006, where he is currently a full professor. His research interest is the area of mechatronics, sensors, actuators, control and preci-sion machine design.
Citations
Citations to this article as recorded by