ABSTRACT
This study proposed a conditional generative adversarial network (cGAN) model for predicting steel plate deformation based on heating line positions in a line heating process. A database was constructed by performing finite element analysis (FEA) to establish relationships between heating line positions and deformation shapes. Deformation shapes were converted into color map images. Heating line positions were used as conditional labels for training and validating the proposed model. During the training process, generator and discriminator loss values, along with MSE and R² metrics, converged stably, demonstrating that generated images closely resembled the actual data. Validation results showed that predicted deformation magnitudes had an average relative error of approximately 3% and a maximum error of less than 7%. These findings confirm that the proposed model can effectively predict steel plate deformation shapes based on heating line positions in the line heating process, making it a reliable predictive tool for this application.
-
KEYWORDS: Line heating, Heating line, Deformation prediction, Image map, conditional GAN
-
KEYWORDS: 선상가열, 가열선, 변형예측, 이미지맵, 조건부 생성적 적대 신경망
1. 서론
선상가열 공정은 강판 표면을 국부적으로 가열하여 원하는 곡률 형상을 형성하는 공정으로, 주로 선박의 선수나 선미 곡블럭 제작에 활용된다. 현재까지 가열 조건과 가열선 위치에 따른 변형 예측은 주로 숙련된 작업자의 경험에 의존하고 있으나, 숙련 인력의 부족과 생산성 향상의 필요성으로 인해 공정의 표준화와 자동화가 필수적으로 요구되고 있다. 이를 실현하기 위해서는 원하는 형상을 얻기 위한 공정 변수를 효과적으로 선정하고, 공정 변수와 강판 변형 간의 관계를 체계적으로 정립하여 변형 형상을 정확히 예측하는 방법을 제시하는 것이 필요하다[
1]. 기존의 변형 예측 방법으로는 실험 기반 계산식, 열탄소성 해석 및 고유변형도법 등이 제안된 바 있다[
1-
3]. 하지만 이러한 접근법은 실험적 제약과 해석 방법의 한계로 인해 다양한 공정 변수를 충분히 고려하기 어렵다는 한계가 있다. 한편, 인공신경망(Artificial Neural Network)을 활용하여 다양한 공정 변수를 반영하면서도 빠르고 정확하게 변형 형상의 예측 가능성을 제시한 연구가 보고되었다[
4]. 특히, 합성곱신경망(Convolutional Neural Network, CNN)을 활용하여 가열선 위치를 예측하는 연구는 가열선을 물체로 간주하고, 가열선과 변형 형상의 관계를 학습하여 주어진 형상에 따라 가열선 위치를 예측하는 방식으로 비교적 높은 정확도를 보였다[
5-
7]. 그러나 이러한 방법은 가열선 인식에 초점이 맞춰져 있어 다양한 변형 형상을 학습하는 데 한계가 있을 수 있다. 최근에는 조건부 생성적 적대 신경망(conditional Generative Adversarial Network, cGAN)이 복잡한 비선형 문제를 효과적으로 처리할 수 있는 강점을 기반으로 변형 예측 분야에서 효과적으로 활용되고 있다[
8,
9]. 특히, 용접 구조물의 변형 예측 연구에서는 cGAN을 활용한 변형 분포가 유한요소법(Finite Element Method, FEM) 결과와 높은 일치를 보였으며, 다양한 변형 형상을 학습하는 데 적합한 가능성을 제시하였다[
10]. 그러나 현재까지 선상가열 공정에 cGAN을 적용하여 변형 형상을 예측한 연구는 보고된 바 없다. cGAN은 복잡한 데이터 분포를 모델링할 수 있는 성능을 갖추고 있어[
11], 다양한 변형 형상을 학습하고 공정 조건에 따른 변형 형상을 효과적으로 예측할 수 있는 가능성을 제공한다.
본 연구에서는 선상가열 공정에서 가열선 위치에 따른 강판 변형을 예측하기 위한 cGAN 모델을 제안하였다. 이를 위해 먼저 유한요소 해석을 통해 다양한 가열선 위치에 따른 강판 변형 데이터를 확보하고, 이를 기반으로 가열선 위치와 변형 형상 간의 관계를 데이터베이스로 구축하였다. 구축된 데이터는 변형 형상을 컬러맵(Color Map) 이미지로 변환하고, 가열선 위치를 조건 레이블(Label)로 설정하여 cGAN 모델의 학습과 검증에 활용하였다. 또한, 반복 학습 과정에서의 성능 변화를 분석하고, 학습된 모델의 검증을 통해 제안된 cGAN 모델이 선상가열 공정에서 변형 형상을 효과적으로 예측할 가능성을 평가하였다.
2. 강판의 선상가열에서 공정 조건과 변형 형상
2.1 가열선 위치에 따른 변형 형상 해석
가로와 세로 길이가 각각 600 mm이고 두께가 10 mm인 연강재판을 속력 5 mm/sec, 입열량 2,380 J/sec의 일정한 조건으로 가열하는 선상가열 공정을 통해 cGAN 모델의 학습 데이터를 확보하였다. 이 공정에서는 가열선 크기가 일정하고, 가열선의 개수는 3개이며, 가열선이 존재할 수 있는 위치가 제한된다고 가정하였다.
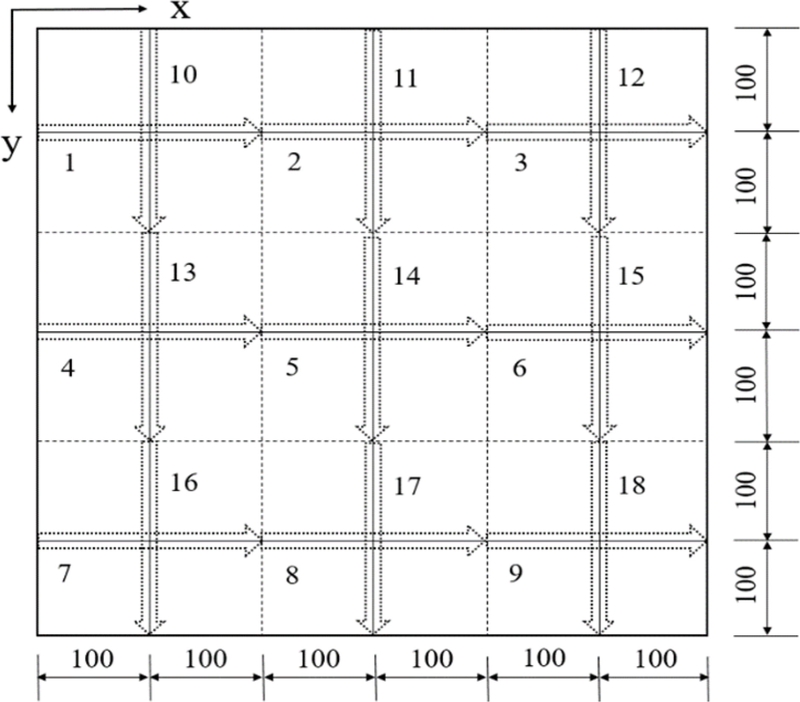
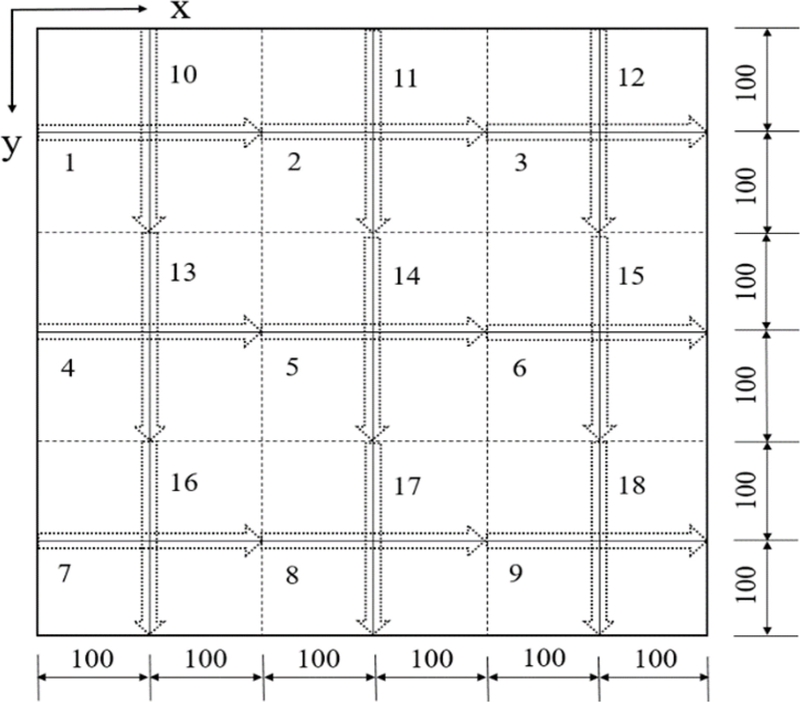
Fig. 1은 이러한 조건을 반영한 가열선의 크기와 위치를 나타낸다[
6]. 가열선의 길이는 200 mm, 가열선 간격은 200 mm로 설정되었으며, 가로 방향 9개(1-9)와 세로 방향 9개(9-18)로 총 18개의 위치가 정의되었다. 이 설정된 18개 위치 중 서로 다른 3개 위치를 조합하면, 총 816개의 가열선 조합이 가능하다. 각 가열선 조합에 의한 가열 및 이로 인해 발생하는 변형 형상을 도출하여, cGAN 모델의 학습에 필요한 데이터로 활용하였다.
Fig. 1Positions of heating lines for the deformed shape of the steel plate
유한요소법에 의한 열변형 해석 결과는 실험 결과와 잘 일치하는 것으로 알려져 있어[
12], 가열선 위치에 따른 강판의 변형형상 데이터는 실제 선상가열 공정을 대신하여 온도 해석 및 열변형 해석을 통해 확보할 수 있다. 본 연구에서는 cGAN 모델의 입력 데이터를 생성하기 위해 한정된 선상가열 공정 조건에서 강판의 온도분포를 이론 해석으로 계산하였고, 열변형 해석은 유한요소법을 활용하여 수행하였다. 가열에 의한 온도 계산은 유한 두께를 가진 무한 평판에서 등속도로 이동하는 점 열원에 대한 Rosenthal의 이론 해를 적용하였다[
13]. 열변형 해석은 상용 소프트웨어를 이용하여 수행하였으며[
14], 강판의 열적 및 기계적 성질이 온도에 따라 변화하는 특성을 반영하였다. 강체 운동을 방지하기 위해 가열선 시작 위치에서 강판 뒷면의 좌우 방향 자유도를 구속하고, 가열선 중앙부 강판 뒷면의 면외 방향 변위를 구속하여 해석을 진행하였다. 해석 결과, 평면 내의 변형은 매우 작아 무시하고 면외 변형만을 변형 데이터로 활용하였다. 제안된 해석 모델을 통해 각 가열선에서의 선상가열로 인한 강판 변형 형상을 예측할 수 있었으며, 1번부터 18번까지의 모든 가열선 위치에 대해 변형 형상 데이터를 확보하였다.
유한요소 해석 모델을 통해 각 가열선에 의한 변형 데이터를 산출하였으며, 서로 다른 3개의 가열선으로 구성된 조합에 의한 변형은, 강판의 폭과 길이에 비해 높이 방향 변형량이 상대적으로 매우 작아 선행 가열로 인한 강성 변화는 미미하다고 가정하고, 해당 조합에 포함된 각 가열선의 변형 크기를 선형적으로 중첩하여 계산하였다. 이를 통해 총 816개의 가열선 조합에 따른 변형 형상을 확보하고 이를 데이터베이스로 구축하였다. 확보된 변형 형상을 cGAN 모델이 입력 데이터로 활용하기 위해, 먼저 변형 데이터를 컬러맵 형상으로 변환하였다.
변형 크기와 컬러맵의 색상 관계를 설정하기 위해, 0.0에서 3.8 mm까지의 변형 크기를 Blue에서 Red로 이어지는 제트(Jet) 컬러맵의 256개 색상 범위에 대응시켰다. 이 과정을 통해 총 816개의 컬러맵 형상을 생성하였으며, 이 중 808개를 학습 데이터로, 나머지 8개를 검증용 데이터로 활용하였다. 검증용 데이터는 모델의 성능을 효과적으로 평가할 수 있도록 전체 데이터의 약 1%를 선정하되, 분포의 균형을 위해 균등한 간격으로 추출하였다.
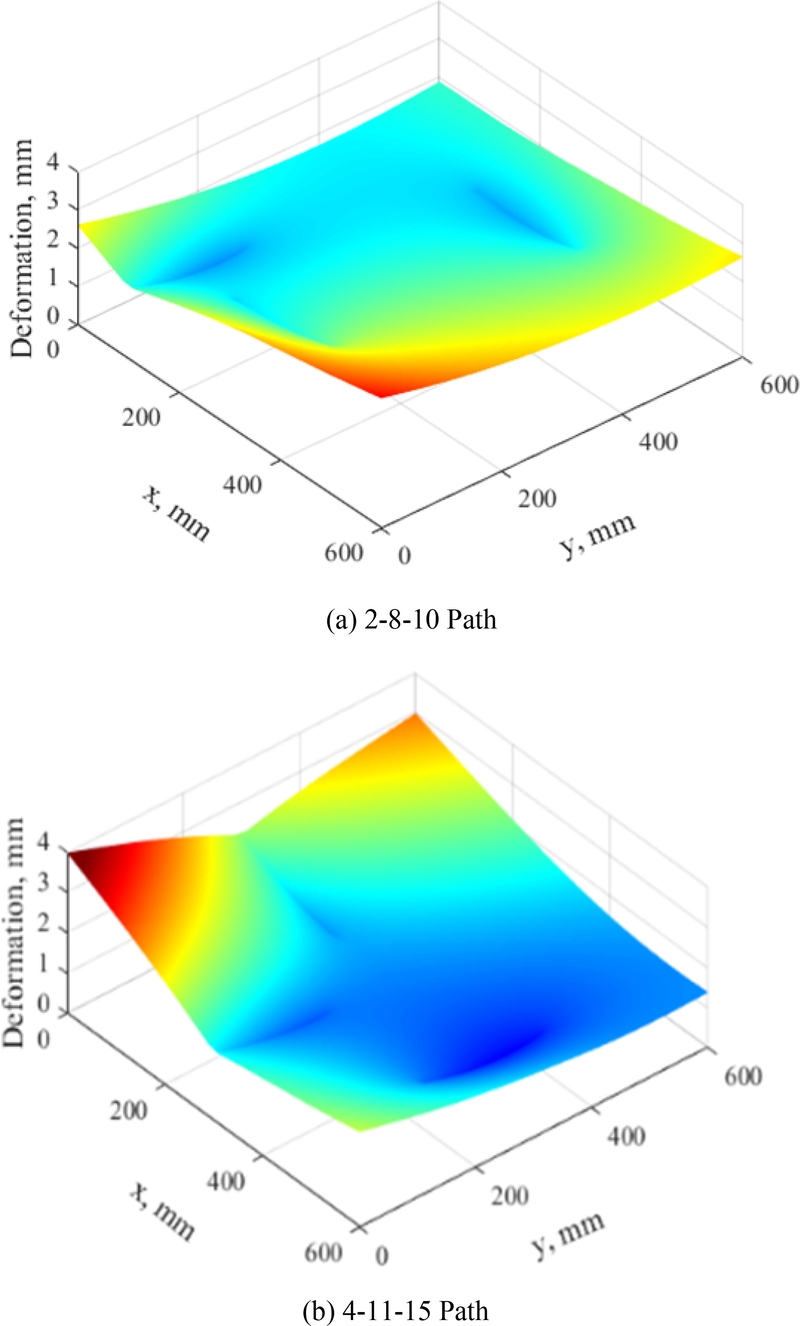
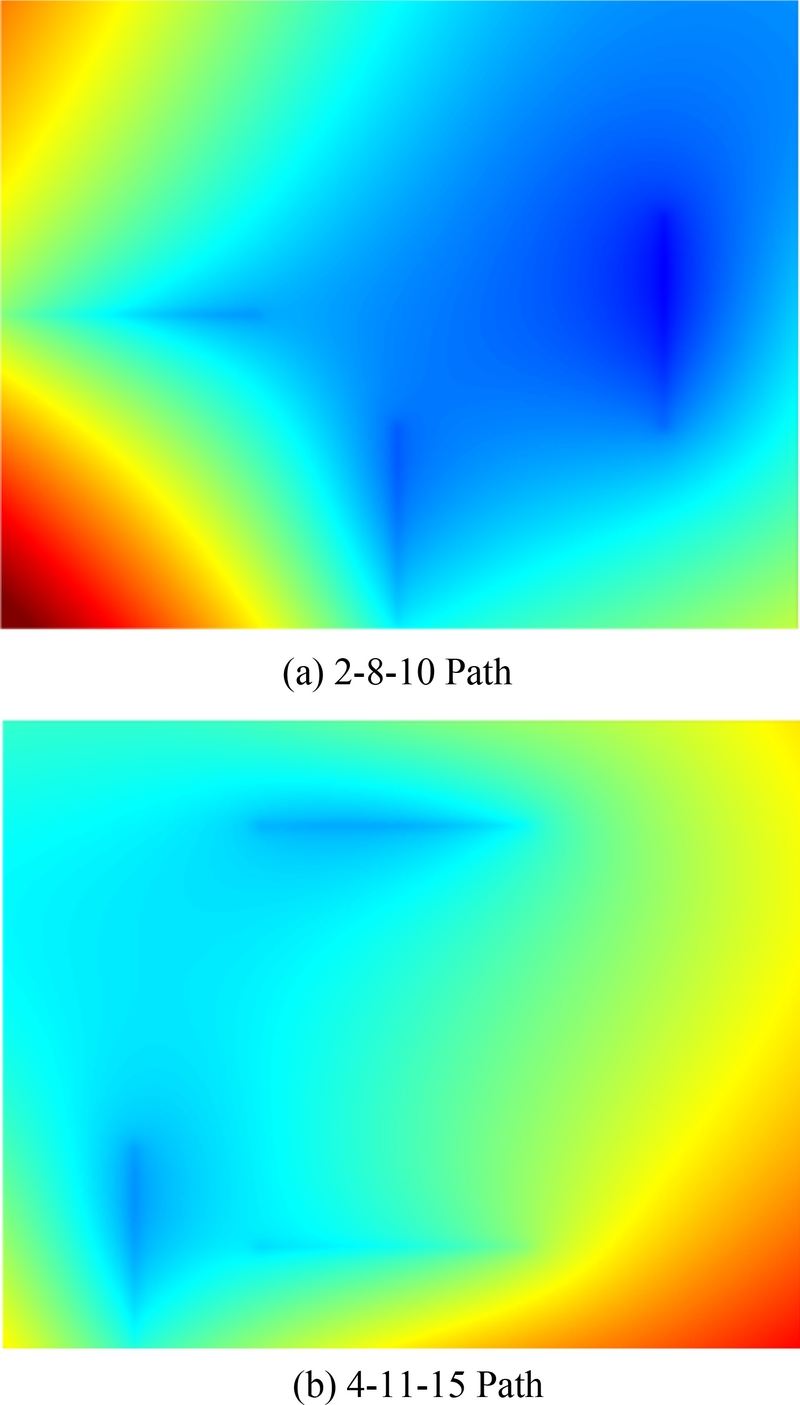
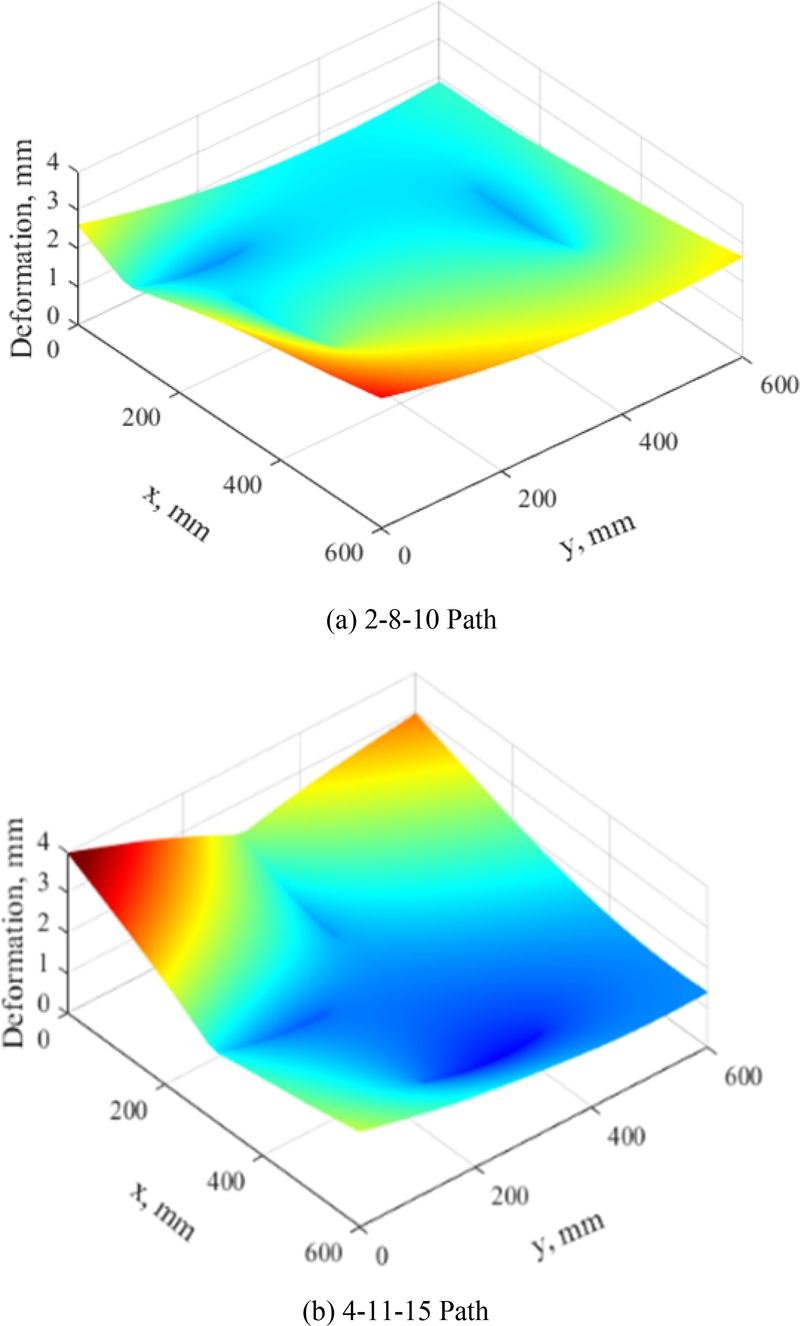
Figs. 2(a)와 2(b)는 각각 2-8-10 경로(Path)와 4-11-15 경로의 두 가지 대표적인 가열선 조합 사례에서 변형 형상을 나타낸다. 각 사례는 3개의 가열선에 의한 변형 해석 결과를 중첩한 크기를 컬러맵으로 나타낸 것이다. 이와 같이 강판에 설정된 x-y 좌표계에 표현된 컬러맵 형상은 535 × 678 픽셀 크기의 컬러맵 이미지로 변환되어 cGAN 모델의 입력 데이터로 사용되었다.
Fig. 2Results of FEM analysis for two sample combinations of heating lines
3. 변형 예측에서 cGAN의 적용
3.1 cGAN 모델
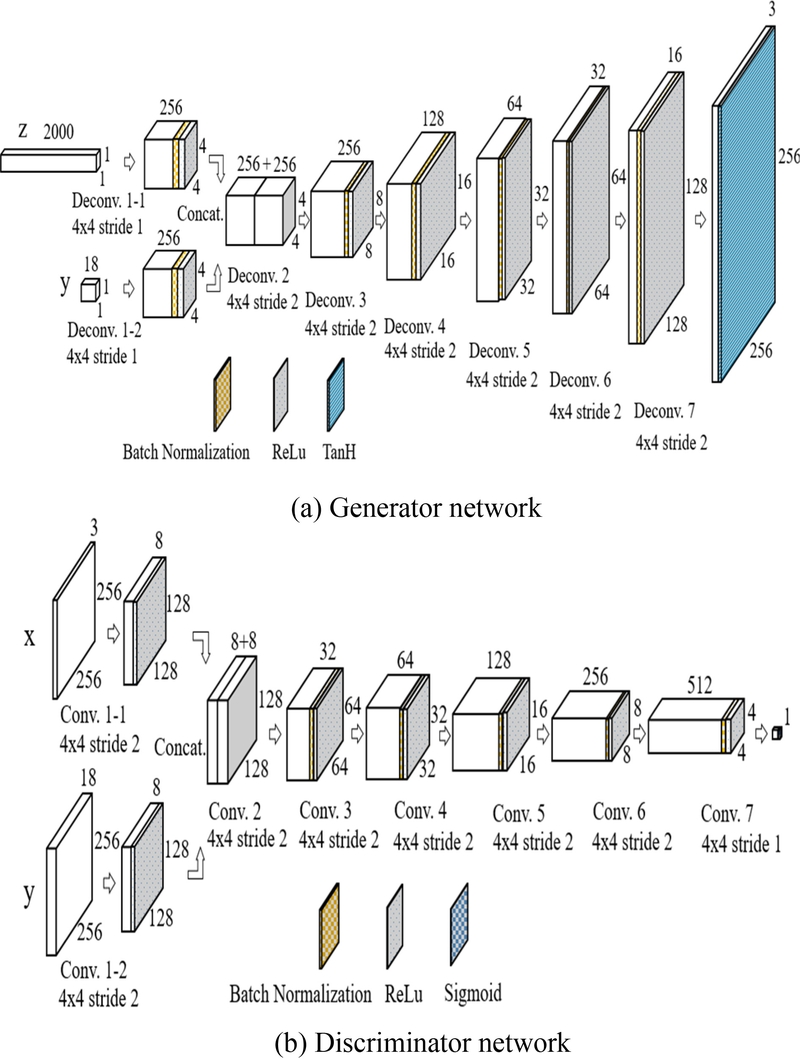
Fig. 3은 제안된 cGAN 모델의 생성자(Generator)와 판별자(Discriminator) 네트워크(Network) 구조를 각각 나타낸 것이다. 이 두 네트워크는 적대적 학습을 통해 최적화되며[
11], 최종적으로 변형 예측 모델로 완성된다.
Fig. 3Architecture of the proposed cGAN model
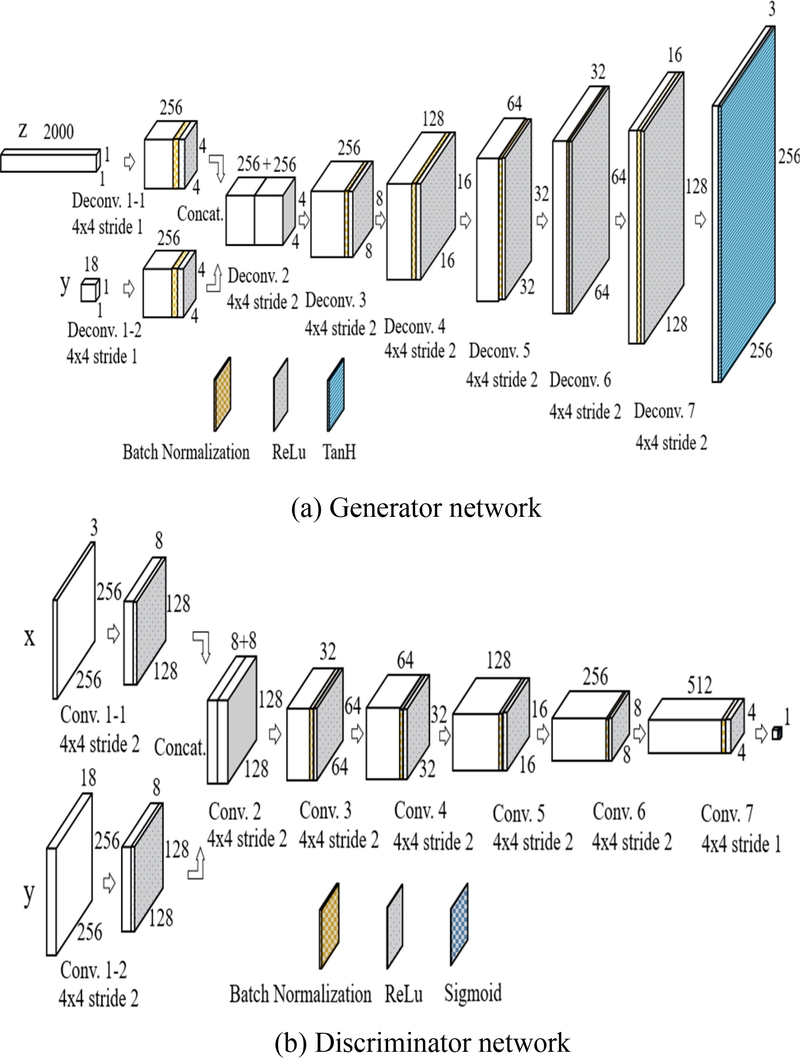
Fig. 3(a)는 생성자 네트워크의 구조와 구성 요소를 나타낸다. 생성자는 잠재 벡터(Latent Vector, z)와 조건 벡터(Label Vector, y)를 입력으로 받아, 실제 이미지와 유사한 이미지를 생성하는 역할을 수행한다. 본 연구에서는 은닉층(Hidden Layer) 6개로 구성된 생성자 네트워크의 기본 구조를 제안하였으며, 잠재 벡터의 차원을 2,000 조건 레이블을 이미지당 18개로 설정하였다. 잠재 벡터와 조건 벡터는 각각 초기 출력 채널 수를 256으로 설정하여 전치 합성곱(Transpose Convolution) 연산을 수행한다. 이때 사용되는 커널(Kernel) 크기는 4 × 4, 스트라이드(Stride)는 1, 패딩(Padding)은 0으로 설정된다. 이를 통해 (256, 4, 4)형태의 특성맵이 생성된다. 각 전치 합성곱 연산 후에는 배치 정규화(Batch Normalization)와 ReLU 활성화 함수가 적용된다. 이후 잠재 벡터와 조건 벡터로부터 생성된 두 특성맵은 채널 차원에서 결합(Concatenation)되어 (256 + 256, 4, 4) 형태의 새로운 특성맵이 생성된다.
중간 레이어에서는 커널 크기 4 × 4, 스트라이드 2, 패딩 1의 설정을 통해, 전치 합성곱 연산을 반복적으로 수행하여 특성맵의 크기를 점진적으로 확장한다. 각 레이어에는 배치 정규화와 ReLU 활성화 함수가 추가된다.
최종 출력 레이어는 전치 합성곱 연산을 통해 256 × 256 × 3 크기의 RGB 이미지를 생성하며, 활성화 함수로 Tanh를 사용한다.
Fig. 3(b)는 판별자 네트워크의 구조를 나타낸다. 판별자는 6개의 은닉층으로 구성된 모델로, 입력 데이터는 256 × 256 크기의 이미지와 해당 이미지에 연관된 18개의 조건 레이블로 이루어져 있다. 판별자의 주요 역할은 입력 이미지가 진짜(Real)인지, 가짜(Fake)인지를 판별하는 것이다.
3개의 채널(R, G, B)를 가진 이미지 데이터(3, 256, 256)을 입력으로 받아 첫 번째 합성곱(Convolution) 연산을 수행한다. 이 연산을 통해 8개의 출력 채널이 생성되며, 커널 크기 4 × 4와 스트라이드 2를 적용하여 이미지의 공간적 크기를 절반(128 × 128)으로 축소한다. 활성화 함수로는 LeakyReLU (α = 0.2)를 사용한다. 조건 레이블 데이터는 18개의 채널로 주어지며, (18, 256, 256)로 준비된다. 커널 크기 4 × 4, 스트라이드 2를 적용한 합성곱 연산을 수행하여 레이블의 공간적 크기를 축소한다. 이 출력에도 LeakyReLU (α = 0.2)를 적용한다. 이후 이미지 데이터와 레이블 데이터에서 생성된 두 특성맵은 채널 차원에서 결합되어 (16, 128, 128) 크기의 텐서를 형성한다.
중간 레이어에서는 이 결합된 텐서를 입력으로 하여 반복적인 합성곱 연산을 수행한다. 초기 입력 채널 16개에서 시작하여, 점진적으로 채널 수를 32, 64, 128, 256, 512로 증가시키는 구조이다. 각 레이어에서는 커널 크기 4 × 4, 스트라이드 2, 패딩 1을 사용하여 특성맵의 공간적 크기를 단계적으로 축소한다. 모든 합성곱 연산 이후에는 배치 정규화를 적용하고, 활성화 함수로 LeakyReLU (α = 0.2)를 사용한다.
최종 출력 레이어에서는 입력 채널 512개를 1 × 1 크기의 특성맵으로 축소하는 합성곱 연산을 수행한다. 이 연산은 커널 크기 4 × 4, 스트라이드 1로 설정되며, 활성화 함수로 Sigmoid를 적용한다. 출력값은 입력 이미지가 진짜인지 가짜인지에 대한 확률을 나타낸다.
생성자와 판별자에서 사용되는 필터들은 고유한 가중치(Weight)와 편향값(Bias)으로 구성된다. 가중치는 평균이 0, 표준편차가 0.02인 정규분포를 따르도록 초기화 되었고, 편향값은 초기에 0으로 설정되었다. 학습 과정에서 필터들은 지속적으로 갱신되고, 이를 통해 각 네트워크의 성능을 점진적으로 향상시킬 수 있다.
3.2 cGAN 모델의 학습
변형 해석 결과로부터 생성된 535 × 678 크기의 컬러맵 이미지 총 808개를 cGAN의 학습 데이터로 활용하였다.
Fig. 4는 이 중 두 개의 대표적인 이미지 사례를 제시한다. 데이터 전처리에서는, 모든 이미지를 256 × 256 크기로 축소한 뒤, 픽셀 값을 0 - 255 범위에서 텐서 형식의 0 - 1 범위로 변환하였다. 이후, 각 채널(R, G, B)에 대해 평균 0.5, 표준편차 0.5로 정규화하여, 픽셀 값이 평균 0, 분산 1에 근접하도록 조정하였다.
Fig. 4Sample color-map images for training the cGAN model
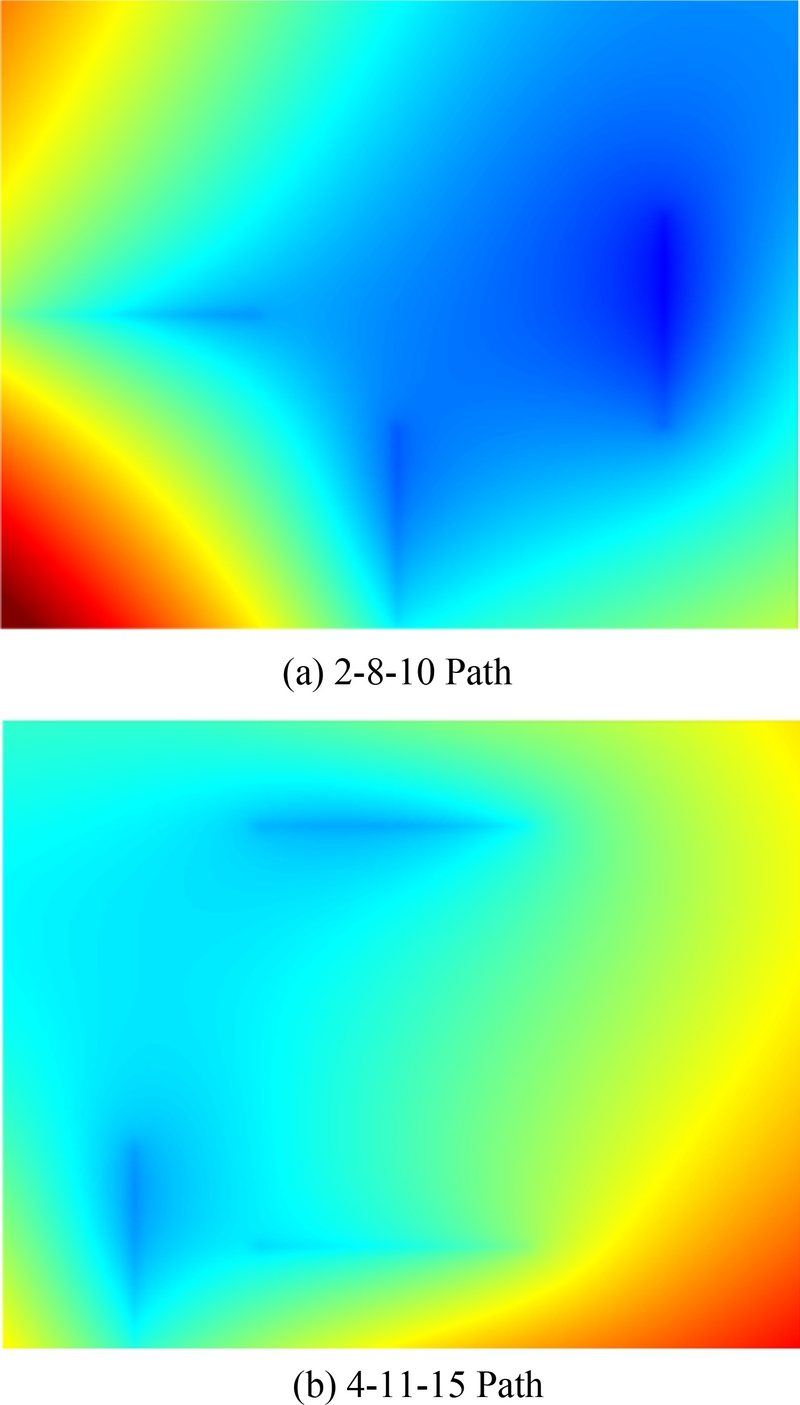
Table 1은
Fig. 4의 각 이미지에 대한 조건 레이블을 나타낸다. 각 이미지의 이름과 1번부터 18번까지의 가열선에 대응되는 열을 매칭시켰으며, 특정 가열선 위치에 가열이 존재할 경우 1, 존재하지 않을 경우 0으로 설정하여, 가열선 정보를 18개 열로 구성된 0과 1의 이진 코드 형태로 나타내었다.
Table 1Label data of the sample images for training the cGAN model
Table 1
|
Image\label |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
|
Img2-8-10.png |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
Img4-11-15.png |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
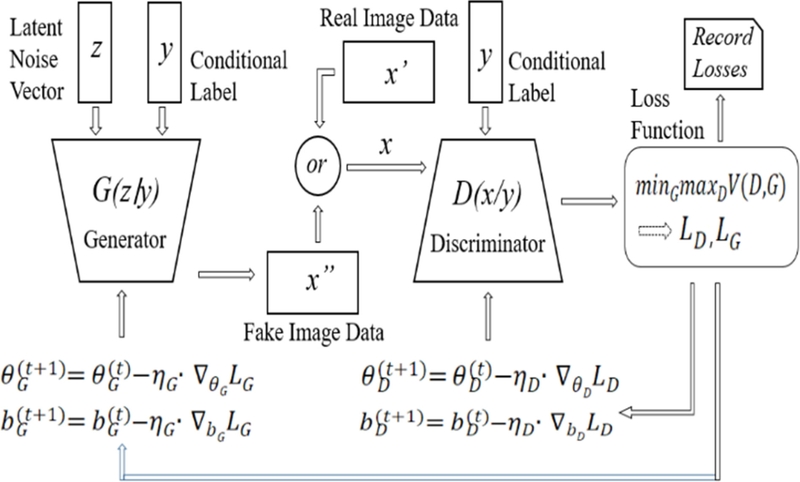
제안된 모델의 학습 과정은
Fig. 5에 나타난 바와 같이 진행된다. 생성자(
G)는 랜덤 노이즈와 조건 레이블을 입력으로 받아 가짜 이미지를 생성한다. 판별자(
D)는 실제 이미지 또는 생성자가 생성한 가짜 이미지와 조건 레이블을 입력으로 받아, 해당 이미지가 진짜인지 가짜인지를 판별한다. 이 과정에는 순전파(Forward Pass)를 통해 전치 합성곱 또는 합성곱 연산을 순차적으로 수행하며, 필터의 가중치(
θ)와 편향값(
b)을 사용하여 특징 맵을 생성한다.
Fig. 5Training process of the cGAN model
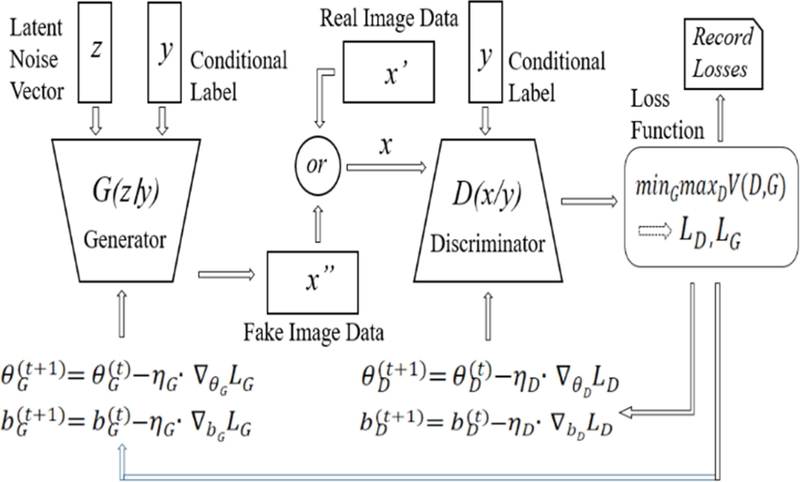
생성된 가짜 이미지는 판별자에 입력되며, 판별자의 출력값을 기반으로 생성자 손실(Loss)을 계산한다. 이때, 가짜 이미지가 판별자에 의해 실제로 인식되도록 생성자의 손실이 계산된다. 반면, 판별자는 실제 이미지는 진짜로, 가짜 이미지는 가짜로 인식되도록 판별자 손실을 계산한다.
생성자와 판별자의 가중치 갱신은 역전파(Backpropagation)와 학습률(η, Learning Rate) 조정을 기반으로 이루어진다. 먼저, 각 필터의 가중치와 편향값에 대한 손실 함수(L)의 기울기(Gradient)를 계산한다. 이후, 계산된 기울기를 바탕으로 경사하강(Gradient Descent)법을 통해 필터의 가중치와 편향값을 갱신한다. 이러한 과정을 반복하면서 생성자와 판별자는 서로의 성능을 향상시킨다. 최종적으로, 생성자는 판별자를 효과적으로 속일 수 있는 가짜 이미지를 생성할 수 있게 된다.
손실 함수(Loss Function)는 cGAN 모델을 훈련하고 필터의 가중치를 최적화하는 데 사용된다. cGAN의 손실 함수는 다음
식 (1)과 같이 정의된 가치 함수(Value Function)에서 유도된다[
11].
여기서 x ~ pdata(x)는 실제 데이터의 확률분포에서 샘플링된 데이터를, z ~ pz(z)는 일반적으로 가우시안 분포에서 샘플링된 임의의 노이즈 데이터를 의미한다.
판별자(
D)의 목표는 가치 함수
V(
D,
G)를 최대화하여 진짜 이미지와 가짜 이미지를 구별하는 것이다. 이를 위해 첫 번째 항은 실제 이미지
x에 대해
D(
x|
y)가 1에 가까워지도록 학습하며, 두 번째 항은 가짜 이미지
G(
z|
y)에 대해
D(
G(
z|
y)|
y)가 0에 가까워지도록 학습한다. 이를 구현하기 위해 BCE (Binary Cross Entropy) 손실 함수를 사용하면 다음
식(2)와 같이 표현할 수 있다.
손실 함수의 첫 번째 항은 실제 데이터 x에 대해 판별자가 1에 가까운 값을 출력하도록 유도하며, 두 번째 항은 생성된 가짜 데이터 G(z/y)에 대해 판별자가 0에 가까운 값을 출력하도록 유도한다. 따라서 이 손실 함수는 판별자가 실제 이미지를 진짜로, 가짜 이미지를 가짜로 구분하는 능력을 최대화하도록 학습한다.
생성자(
G)의 목표는 가치 함수를 최소화하는 것이다. 가치 함수의 우변 첫 번째 항은 생성자와 관련이 없어, 두 번째 항을 최소화하도록 학습된다. 이를 재구성하여, 다음
식(3)과 같은 형태의 BCE 손실 함수로 나타낼 수 있다.
생성자는 이 손실 함수를 통해 가짜 데이터 G(z|y)에 대해 판별자가 1에 가까운 값을 출력하도록 학습된다. 이를 통해 더욱 진짜 같은 이미지를 생성하게 된다.
손실 계산 과정에서는 미니배치(Mini Batch) 방식을 적용한다. 한 번의 역전파 단계에서 생성자는 미니배치 내 여러 이미지를 생성하고, 판별자는 이들 각각에 대한 판별 결과를 제공한다. 이후 미니배치에 포함된 모든 샘플에 대한 BCE 손실을 평균하여 미니배치 손실로 계산한다.
학습 과정에서는 생성자와 판별자를 동시에 학습하지 않고, 한 네트워크를 고정한 상태에서 다른 네트워크를 학습 및 갱신하는 교차 학습 방식을 적용한다. 초기 학습률은 0.0002로 설정하였으며, 가중치와 편향값의 갱신을 위해 Adam 최적화 알고리즘을 적용하였다. Adam의 초매개변수는 β1 = 0.5, β2 = 0.999로 설정하였다. 또한, 학습률 감소 스케줄러를 적용하여 각 학습 에포크(Epoch) 후 평균 손실값을 기반으로 학습률을 동적으로 변화시켰다. 제안된 cGAN 모델의 생성자, 판별자, 학습과정 등 모든 구성요소는 PyTorch 모듈을 사용하여 구현하였다[
15].
본 연구에서는 cGAN 모델의 학습 성능을 평가하기 위해, 판별자와 생성자의 손실 함수를 분석하였고, 평균 제곱 오차(Mean Squared Error, MSE)와 결정계수(Coefficient of Determination, R
2)라는 두 가지 정량적 평가 지표를 활용하였다[
10].
MSE는 예측된 값과 실제 값 간의 평균 제곱 오차를 측정하는 지표로, 모델이 생성한 이미지와 실제 이미지 간의 픽셀 단위 차이를 평가한다. MSE는 다음
식(4)와 같이 정의된다.
여기서 N은 이미지의 개수, W와 H는 이미지의 너비와 높이, Ireal,i,w,h는 실제 이미지 i의 위치 (w, h)에서의 픽셀 값, Igen,i,w,h는 생성된 이미지 i의 동일 위치에서의 픽셀 값을 나타낸다. MSE 값이 낮을수록 모델이 생성한 이미지가 실제 이미지와 더 유사함을 의미한다.
R
2는 모델이 데이터를 얼마나 잘 설명하는지를 나타내는 지표로, 예측값과 실제값 사이의 상관관계를 정량적으로 평가한다. R
2는 다음
식(5)와 같이 정의된다.
여기서 yi는 실제 값, y^l는 모델의 예측값, y-는 실제 값의 평균을 의미한다. 분자 ∑i=1nyi-y^l2는 모델이 설명하지 못한 오차의 제곱합으로, 예측값과 실제값 간의 차이에 따라 변화하며 값이 클수록 모델의 성능이 떨어짐을 나타낸다. 분모 ∑i=1nyi-y-2는 전체 데이터의 변동성을 나타내며, 예측값과 는 독립적으로 실제 값과 그 평균값에 의해 결정된다. R2 값이 1에 가까울수록 모델이 데이터를 잘 설명하고 있음을 의미한다.
본 연구에서는 제안된 cGAN 모델의 최적화를 위해 다양한 초매개변수 설정을 실험하였다. 생성자의 입력 차원은 초기값을 2,000으로 설정한 뒤 3,000과 1,000으로 변경하여 입력 차원 변화가 성능에 미치는 영향을 평가하였다. 또한, 배치 크기(Batch Size)를 16과 32로 설정하여 비교 실험을 수행하였다. 아울러, 모델의 은닉층 개수를 5개와 6개 조정하여 학습 성능의 변화를 관찰하였다.
Table 2에서는 생성자 차원 2,000, 배치 크기 32, 은닉층 6개를 기본 설정(2000_32)으로 두고, 초매개변수 변화 조합과 각각의 색인을 요약하여 제시하였다.
Table 2Changes in hyperparameters and their indices
Table 2
|
|
Latent dimension |
Batch size |
Number of layer |
Index |
|
1 |
1,000 |
32 |
6 |
1000_32 |
|
2 |
2,000 |
32 |
6 |
2000_32 |
|
3 |
3,000 |
32 |
6 |
3000_32 |
|
4 |
2,000 |
16 |
6 |
2000_16 |
|
5 |
2,000 |
16 |
5 |
2000_16_5 |
3.4 학습된 cGAN 모델의 검증
본 연구에서 cGAN 모델의 학습 결과, 은닉층 6개로 구성된 생성자에 입력 차원 2,000과 배치 크기 16을 설정한 경우 가장 우수한 성능을 보였다. 이에 따라, 해당 설정을 기반으로 모델 성능 검증을 수행하였다.
Table 3은 검증을 위해 준비된 8개의 레이블 데이터 세트를 보여주고 있으며, 이 데이터는 하나의 배치로 적용되었다. 학습된 생성자 모델은 이러한 레이블 데이터와 랜덤 노이즈 벡터를 입력으로 받아 8개의 이미지를 생성하며, 각각의 이미지는 256 × 256 크기로 출력되었다. 생성된 이미지는 검증 목적에 맞게 535 × 678 크기로 재조정하여 개별 이미지 파일로 저장하였다.
Table 3Labels for the verification of the trained generator network of the cGAN model
Table 3
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
|
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
|
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
|
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
|
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
생성된 이미지는 검증용으로 준비한 8개의 실제 이미지와 비교하여 생성자의 이미지 생성 능력을 평가하였다. 또한 생성된 컬러맵 이미지와 실제 컬러맵 이미지를 각각 강판의 면외 변형 데이터로 변환하여 검증하였다. 변환된 데이터는 수평 중심선(Horizontal Centerline)과 수직 중심선(Vertical Centerline)을 따라 변형 크기를 측정한 후, 이를 그래프로 시각화하여 비교하였다.
모델 성능을 정량적으로 평가하기 위해 상대 오차(Relative Error)를 정의를 하였으며, 다음
식(6)과 같이 표현된다.
여기서 P는 생성된 이미지에서 예측된 변형 크기, A는 실제 이미지에서 변환된 변형 크기를 나타낸다.
4. 결과 및 고찰
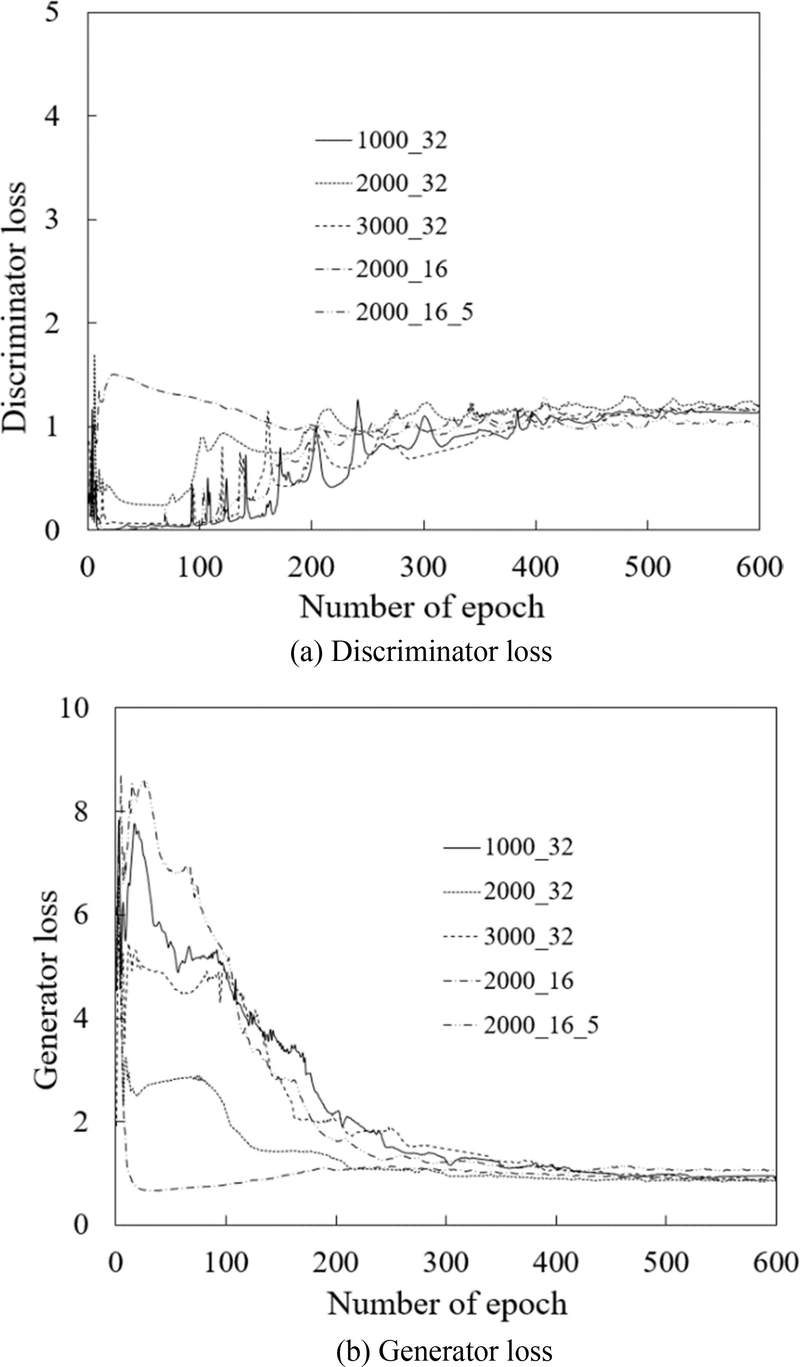
Figs. 6(a)와 6(b)는 제안된 cGAN 모델을 600 에포크 동안 학습한 결과로, 판별자와 생성자의 손실 변화를 각각 나타낸다. 초매개변수 설정에 따라 약간의 차이는 있지만, 학습 초기에는 손실값은 변화폭이 크다가 약 400 에포크 이후는 손실이 안정적으로 수렴하는 양상을 보였다. 이는 두 네트워크가 균형 상태에 도달했음을 시사한다.
Fig. 6 Changes in the losses of the proposed model with the number of epochs
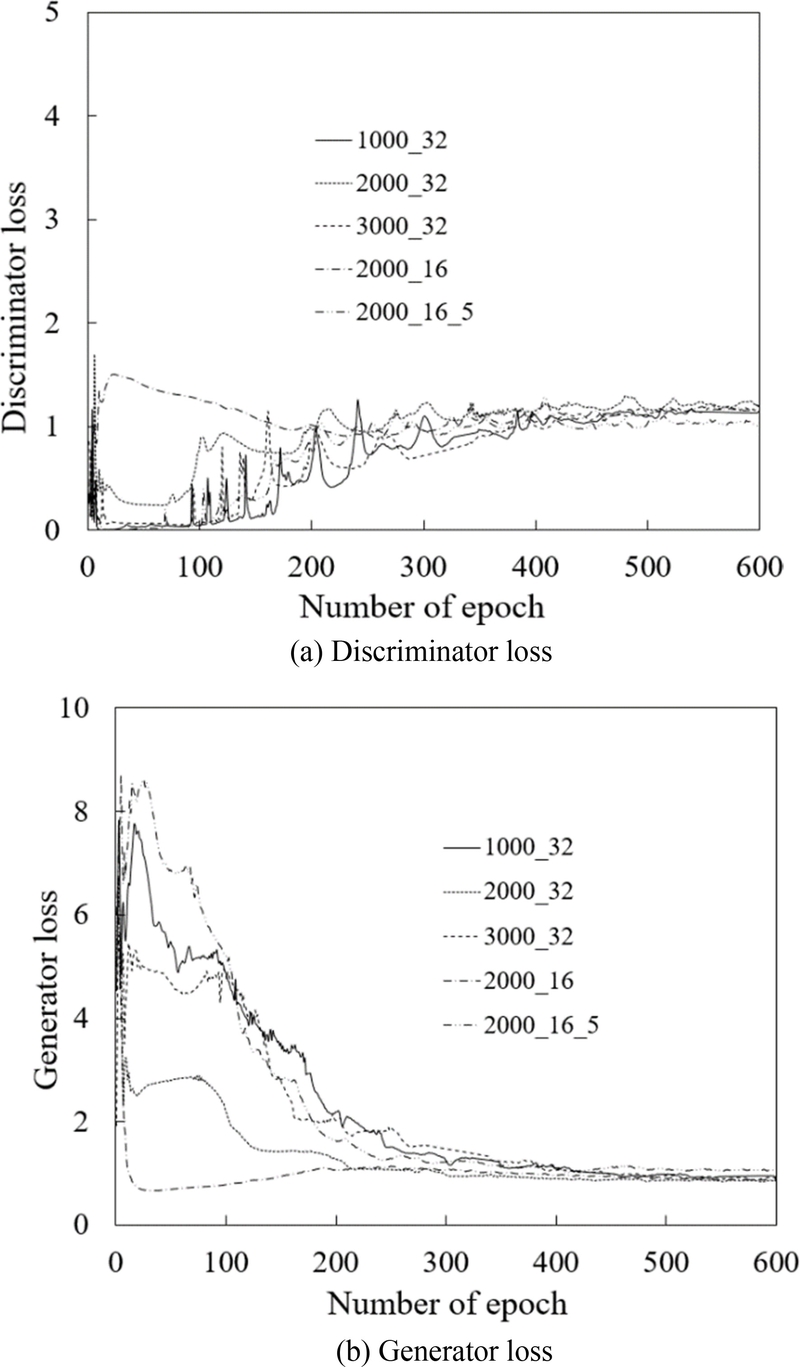
학습 초기에 생성자의 손실값은 약 8 근처의 높은 값을 보였다. 이는 생성된 데이터가 진짜 데이터 분포와 크게 달라, 판별자가 이를 쉽게 가짜로 예측하기 때문이다. 그러나 학습이 진행됨에 따라 생성자가 점점 더 진짜 같은 데이터를 생성하게 되고, 판별자는 이를 구분하는 데 어려움을 겪으며, 판별자 손실은 증가하고 생성자 손실은 감소하는 경향을 나타낸다.
생성자 차원이 2,000인 기본 설정에서는, 판별자와 생성자의 손실값은 각각 1.195와 0.846으로 수렴하였다. 생성자 차원을 1,000과 3,000으로 변경한 경우, 판별자와 생성자 손실은 각각 1.149와 0.903 그리고 1.16과 0.919로 나타났다. 생성자 차원을 증감할 경우, 판별자 손실은 점진적으로 증가하고, 생성자 손실은 점진적으로 감소하는 경향을 보였다. 특히, 100-400 에포크 구간에서는 생성자의 손실 변동이 더 뚜렷하게 나타났다.
배치 크기를 16으로 줄였을 경우, 판별자와 생성자의 손실값은 각각 1.21과 0.87로 수렴하였다. 학습 초기에는 판별자 손실이 급격히 증가하여 23 에포크에서 1.508에 도달하였고, 생성자 손실은 35 에포크에서 0.667로 최소값을 기록하였다. 학습 과정에서 판별자와 생성자의 손실값은 국부적인 변동이 거의 없었으며, 판별자 손실이 1.21로 유지된 것은 이론적인 중립 상태인 1.386에 가까운 값으로, 생성자가 진짜 같은 데이터를 어느 정도 생성하고 있음을 나타낸다. 배치 크기가 16일 때의 손실값 변화는 판별자의 성능 변화와 생성자의 데이터 생성 능력 간의 상호작용을 잘 보여준다.
학습 초기에는 판별자가 가짜 데이터를 쉽게 구분하였으나, 학습 중반부에는 생성자의 성능이 개선되면서 판별자가 구분하기 어려워지는 시점에 손실값의 극값이 나타났다. 이후에는 생성자와 판별자가 균형 상태에 도달하면서 손실값이 안정적으로 수렴하였다.
한편, 은닉층 수를 5로 줄인 경우에는 판별자와 생성자의 손실값이 각각 0.995와 1.056로 수렴하였으며, 초기 학습 단계에서 생성자 손실이 큰 값을 보였다. 이는 은닉층 축소로 인해 모델의 표현력이 저하되었음을 시사한다.
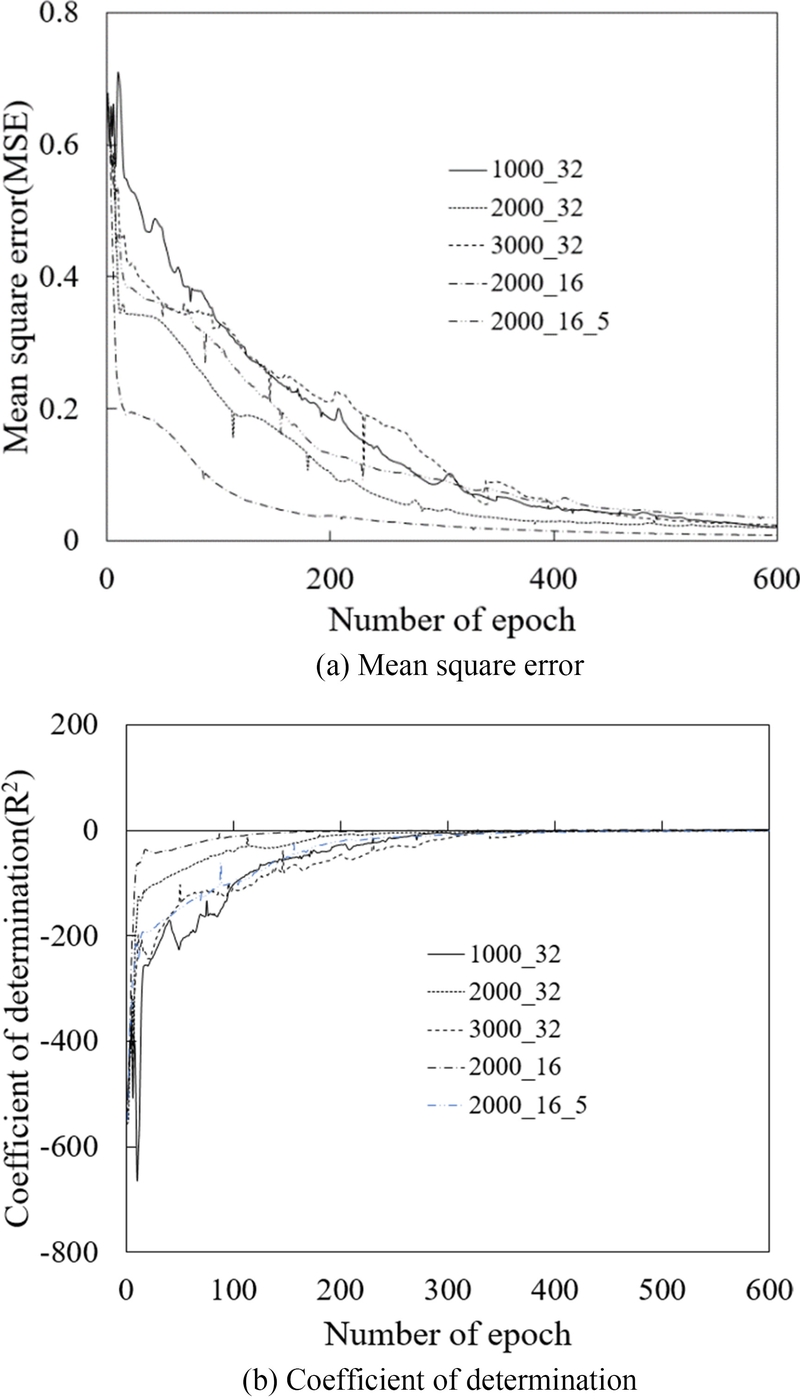
Fig. 7은 MSE와 R
2를 사용하여 제안된 모델의 학습 성능을 평가한 결과를 나타낸다. 학습 에포크가 증가함에 따라 MSE는 빠르게 감소하고, R²가 크게 증가하며, 400 에포크 이후에는 안정적으로 수렴하는 양상을 나타냈다. 이는 반복 학습을 통해 모델의 변형 예측 성능이 꾸준히 향상됨을 나타낸다.
Fig. 7 Changes in two measures for evaluating the training performance of the proposed model with the number of epochs
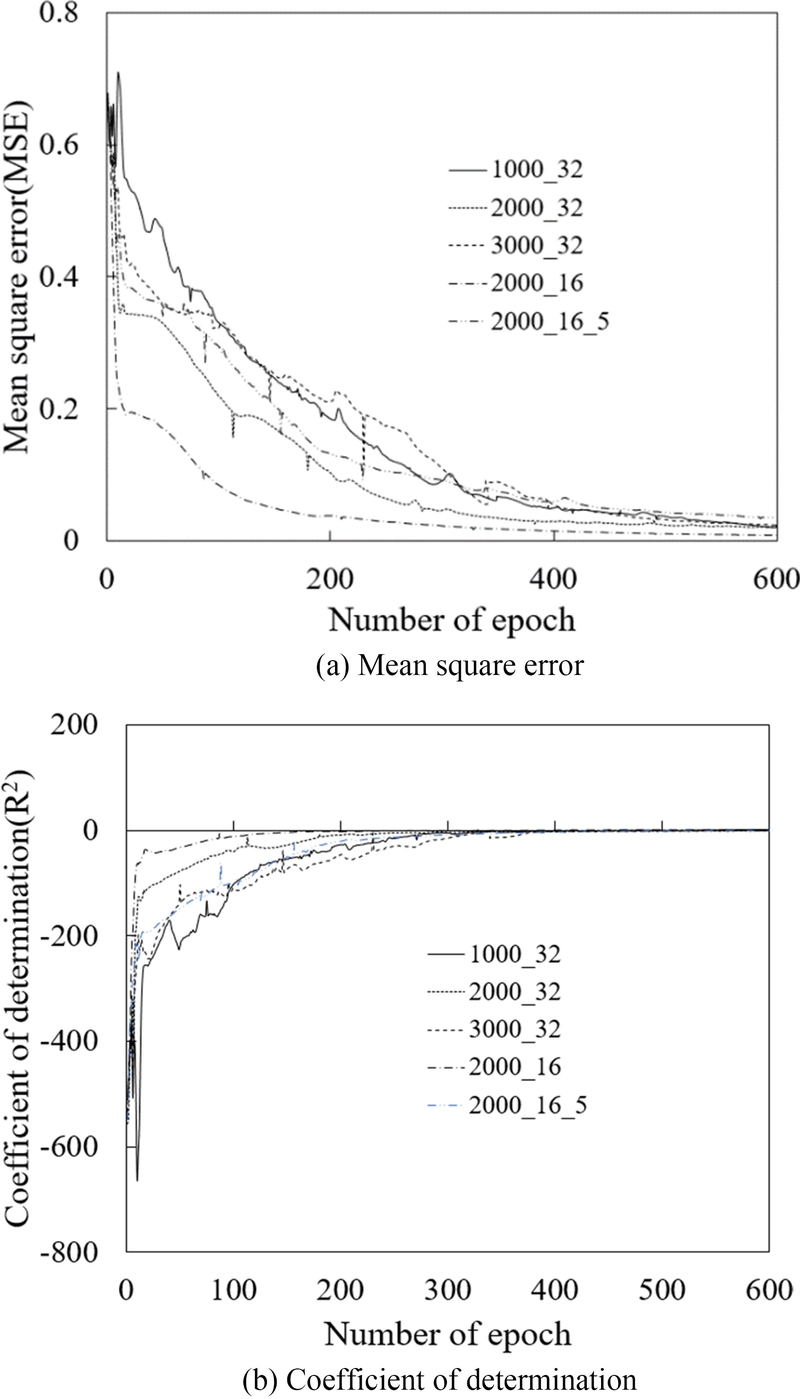
은닉층 수 6개, 생성자 차원 2,000 배치 크기 32의 기본 설정에서 MSE는 약 400 에포크에서 수렴하여 최종적으로 0.02에 도달하였다. 반면, 생성자 차원을 1,000 또는 3,000으로 변경한 경우, MSE의 수렴 속도가 느려지고, 최종 수렴값도 0.02보다 다소 높게 나타났다. 배치 크기를 16으로 줄였을 경우, 초기 학습 단계에서 MSE가 빠르게 감소하며, 최종적으로 0.008에 수렴하였다. 그러나 은닉층 수를 5로 줄인 경우, MSE의 수렴 속도가 저하되었고, 최종적으로 0.034의 값을 기록하였다.
학습 초기에는 예측값이 실제 평균에서 크게 벗어나 있어 R2가 음수로 나타났으나, 반복 학습을 통해 모델이 실제 데이터의 변동성을 점차적으로 포착하는 모습을 보였다. 기본 설정에서 R2는 학습 초기 약 -556.5로 매우 낮게 시작하였으나, 540 에포크 이후 0.035로 수렴하였다. 생성자 차원을 1,000으로 줄이거나 3,000으로 증가하면, R2의 개선 속도가 둔화되고, 학습 중 국부적인 변동이 더 크게 나타나며, 600 에포크에서 -0.1로 수렴하였다. 배치 크기를 16으로 줄인 경우, R2는 초기 학습 단계에서 빠르게 증가하며, 학습 종료 시점인 590 에포크 이후 0.145로 수렴하였다. 반면, 은닉층 수를 5로 줄이고 배치 크기를 16으로 설정한 경우, R2는 학습 초기의 개선 속도가 상대적으로 낮았으며, 최종적으로 -1.7로 수렴하여 기본 설정에 비해 낮은 성능을 보였다.
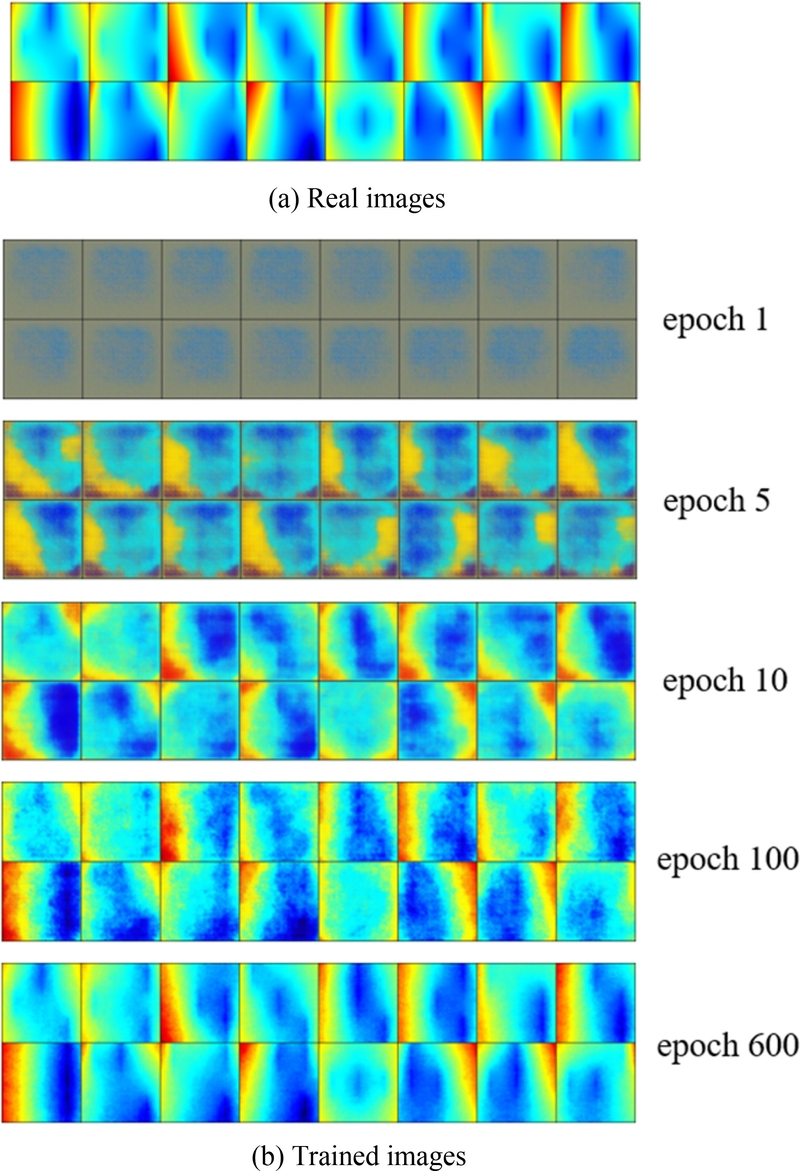
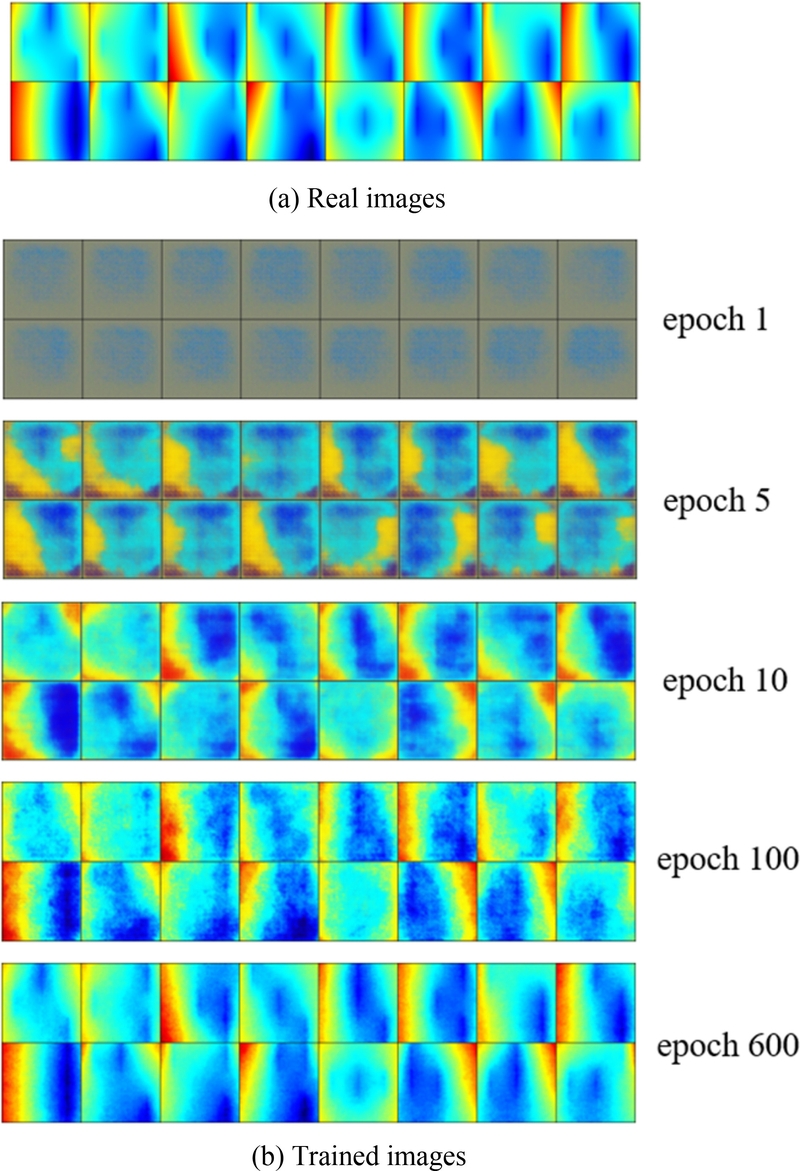
Fig. 8은 기본 설정에서 배치 크기를 16으로 축소하여 학습한 경우, 반복 학습 과정에서 생성자의 이미지 생성 능력을 나타낸다.
Fig. 8(a)는 학습에 사용된 실제 강판 변형의 컬러맵 이미지 중 임의의 한 배치를 나타낸다.
Fig. 8(b)는 학습이 진행됨에 따라 제안된 모델의 생성자가 생성한 이미지의 변화를 시각적으로 나타낸다. 초기 5 에포크까지는 생성된 이미지가 흐릿하고 실제 이미지와 전혀 다른 형태를 보였다. 그러나 약 10 에포크에 이르러 생성자의 성능이 개선되면서 구분 가능한 컬러맵 이미지를 생성하기 시작했다. 100 에포크에서는 모델의 학습이 안정화되어 생성된 이미지가 실제 이미지와 유사한 품질을 보였다. 이는 생성자가 실제 이미지의 확률 분포를 효과적으로 학습하여, 유사한 형태와 분포를 가진 이미지를 생성하고 있음을 나타낸다. 600 에포크 학습 후에는 배치 내에서 생성된 각 이미지가 실제 이미지와 매우 유사한 결과를 보였다. 이러한 결과는 실제 데이터를 기반으로 성공적으로 학습했음을 보여주며, 학습 성능이 양호하다고 평가할 수 있다.
Fig. 8 Comparison of real images and trained images obtained at different epochs for a sample batch
학습 성능 평가 결과, 6개의 은닉층을 가진 모델에서 생성자 차원을 2,000 배치 크기를 16으로 설정하여 학습한 경우가 최적의 결과를 나타냈다.
이를 바탕으로 학습된 생성자 모델의 변형 예측 성능을 검증하였다. 성능 검증은
Table 3에 제시된 조건 레이블 세트를 적용하여 수행되었다.
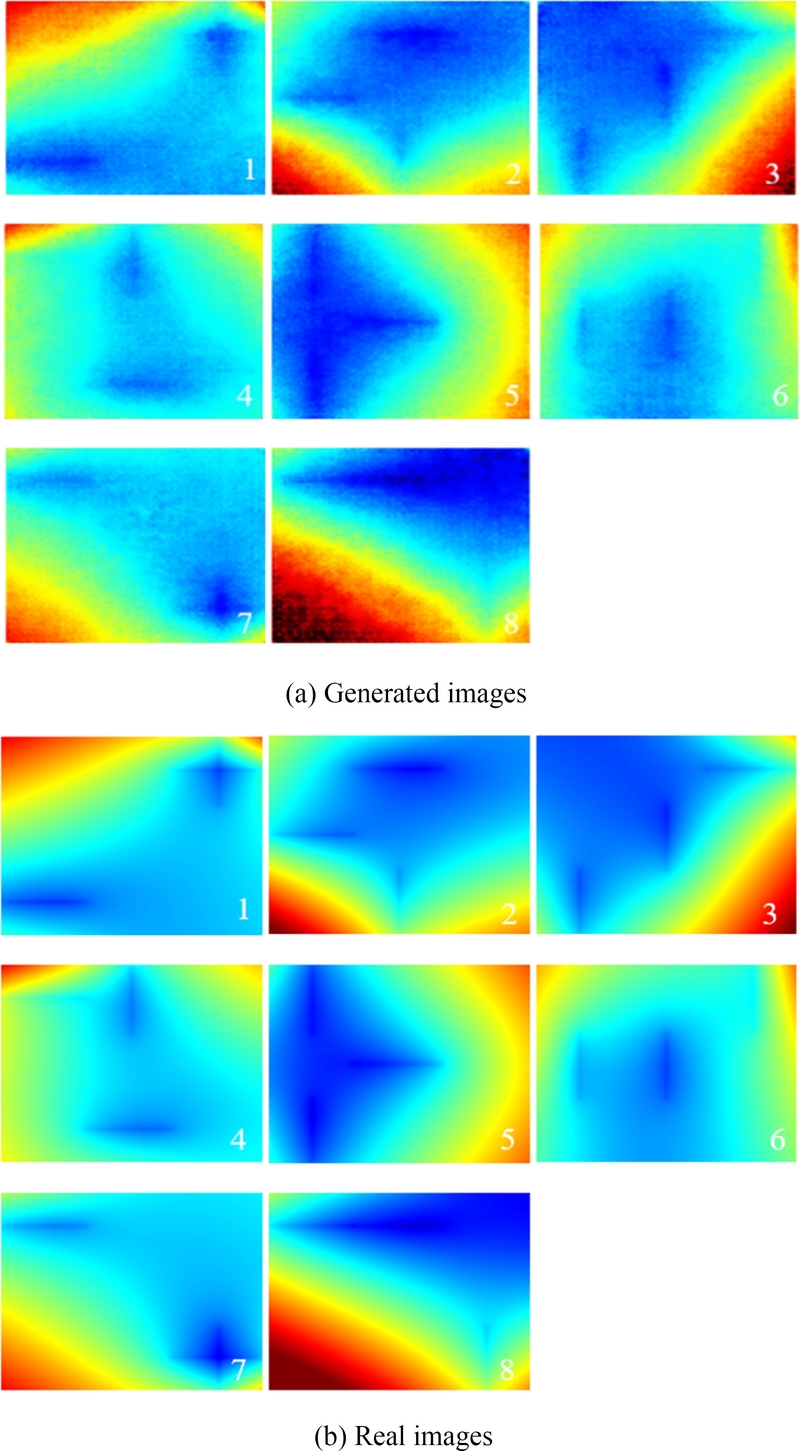
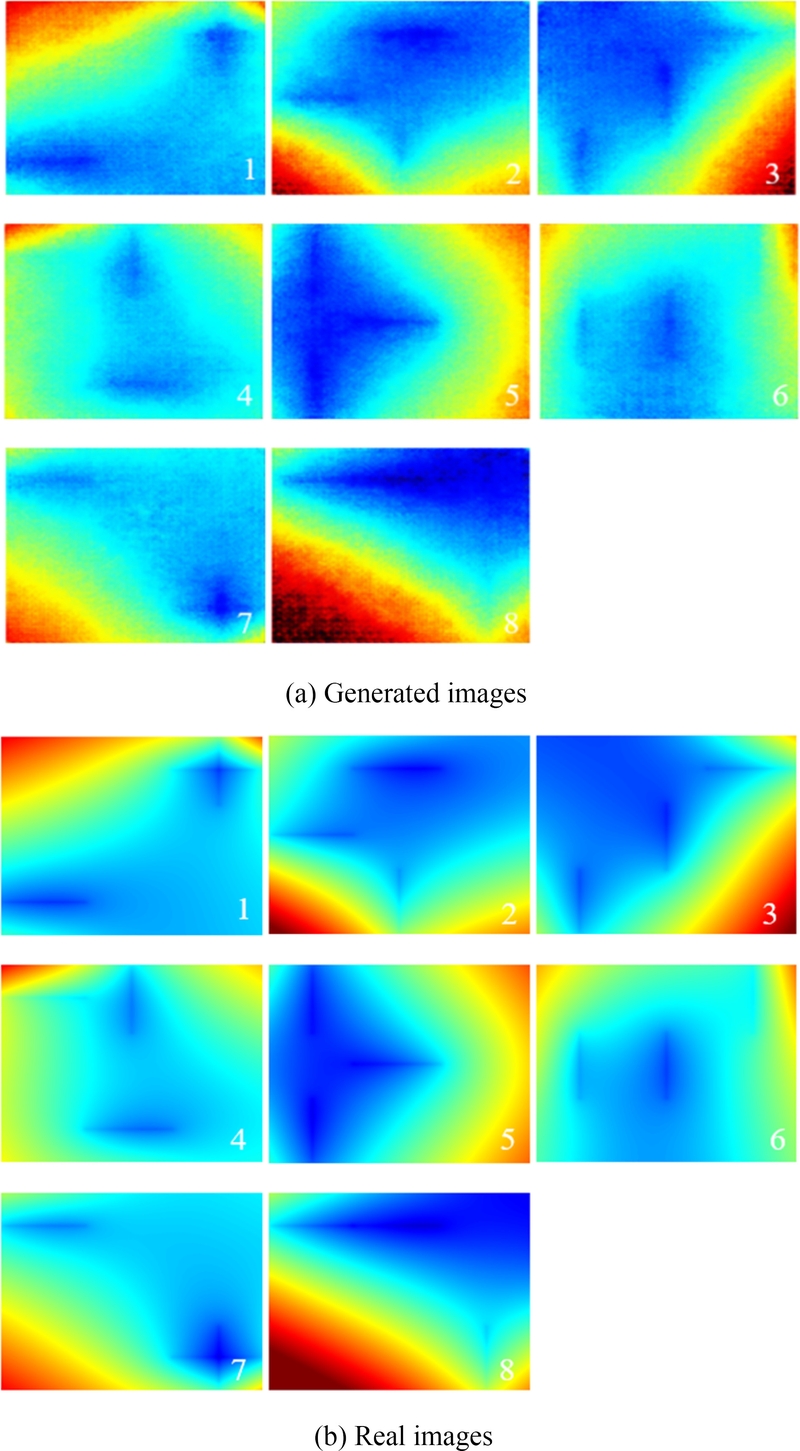
Fig. 9는 제안된 모델의 성능 검증 결과를 시각적으로 나타낸다.
Fig. 9(a)는 조건 레이블에 따라 생성자가 출력한 8개의 이미지를 보여주며, 이는 제안된 cGAN 모델이 가열선 위치를 나타내는 조건에 따라 예측한 컬러맵 이미지이다. 이 결과는 강판 변형의 크기 정보를 포함하고 있다.
Fig. 9(b)는 각 조건 레이블과 동일한 가열선 위치에서 가열했을 때, 각 가열선의 수치해석 결과를 선형적으로 중첩하여 산출한 변형 데이터를 컬러맵 이미지로 표현한 것으로, 변형의 실제 결과를 시각적으로 나타낸다. 8개 사례를 비교한 결과, 생성된 이미지는 실제 이미지와 대체로 유사한 경향을 보였다. 이를 통해 제안된 모델이 강판 변형을 양호하게 예측할 수 있음을 확인할 수 있다.
Fig. 9 Comparison between generated images with the proposed model and corresponding real images
생성자가 생성한 이미지와 실제 이미지의 컬러맵을 각각 변형 데이터로 변환하여 두 변형 데이터를 비교하였다.
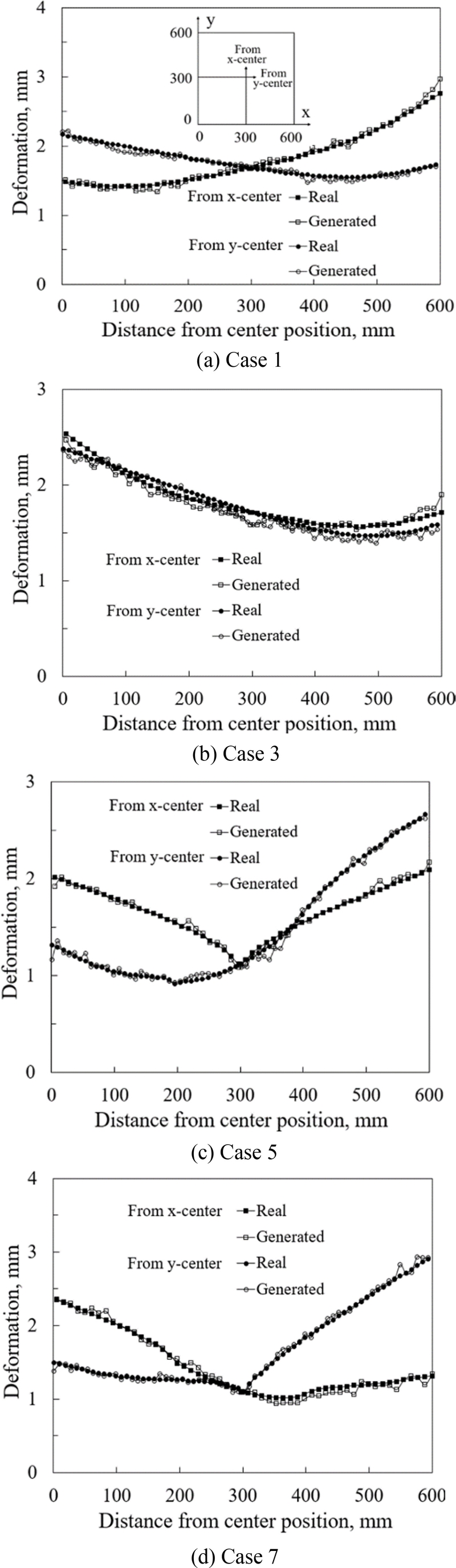
Fig. 10은 검증을 위한 레이블 세트 중 1, 3, 5, 7번 사례에서 강판의 폭 방향과 길이 방향 중심선을 따라 나타나는 변형 크기를 비교한 결과를 제시한다.
Fig. 10 Comparison between generated deformations and real deformations for four sample cases
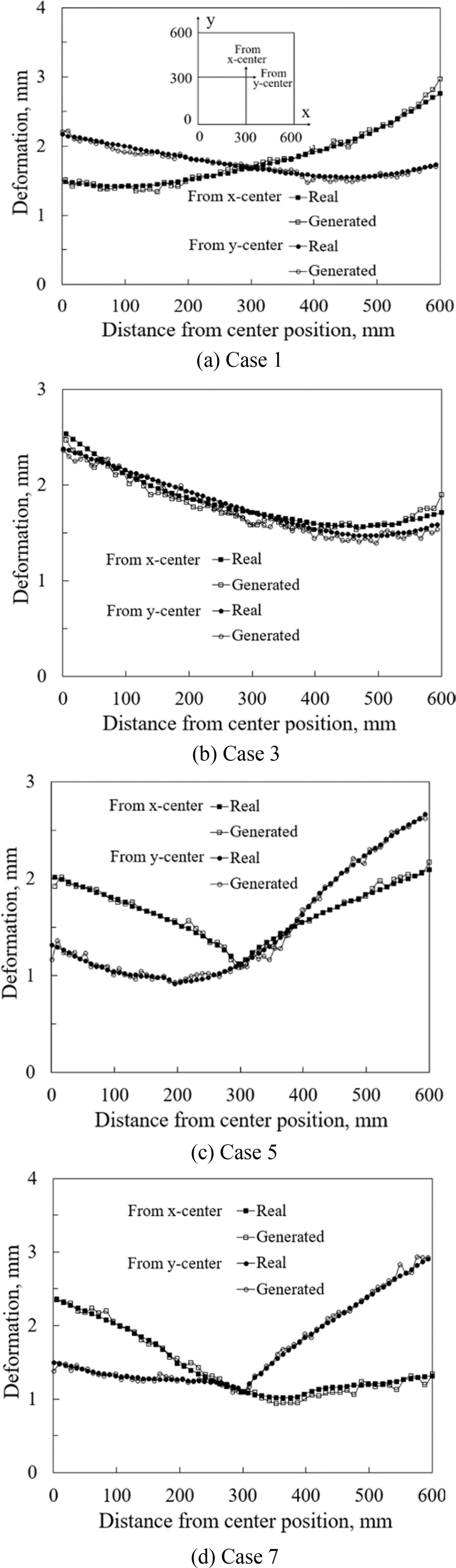
각 사례에서는 가열선의 위치에 따라 변형 크기가 다르게 나타나는 것을 확인할 수 있으며, 제안된 모델이 생성한 변형 크기는 실제 변형 크기와 매우 유사한 경향을 나타낸다. 다소의 편차는 존재하지만, 전반적으로 제안된 모델이 실제 변형 데이터를 잘 예측하고 있음을 확인할 수 있다.
Table 4는 각 조건 레이블에 따른, 실제 변형 크기에 대해 생성자 모델이 예측한 크기의 상대 오차 값을 나타낸다. 제안된 모델이 예측한 변형은 실제 변형에 대하여 최대 7%의 상대 오차를 나타내며, 평균적으로는 약 3%의 상대 오차를 기록하였다. 이는 예측 오차가 비교적 작음을 의미하여, 다양한 가열 조건에서도 제안된 모델은 우수한 변형 예측 성능을 나타낸다고 할 수 있다.
Table 4 Relative error of the predicted deformation with respect to the actual deformation for each condition
Table 4
|
|
y-direction (x = 300 mm) |
x-direction (y = 300 mm) |
|
1 |
0.022 |
0.019 |
|
2 |
0.023 |
0.026 |
|
3 |
0.030 |
0.029 |
|
4 |
0.036 |
0.048 |
|
5 |
0.014 |
0.025 |
|
6 |
0.070 |
0.041 |
|
7 |
0.035 |
0.020 |
|
8 |
0.028 |
0.018 |
5. 결론
본 연구에서는 선상가열 공정에서 가열선 위치에 따른 강판의 변형 형상을 효과적으로 예측하기 위해 조건부 생성적 적대 신경망(cGAN) 모델을 제안하고, 이를 학습 및 검증하였다. 제안된 모델의 학습을 위해, 유한요소 해석을 통해 가열선 위치별 강판 변형 데이터를 확보하고 이를 데이터베이스화하였다. 제안된 모델의 학습 및 성능 검증은 생성자와 판별자의 손실값, MSE, R2 지표를 기반으로, 은닉층 수, 생성자 입력 차원, 배치 크기 등 초매개변수의 변화를 고려하여 수행되었으며, 이를 통해 다음과 같은 결론을 도출하였다.
(1) 조건 레이블을 활용하여 컬러맵 이미지를 생성하는 과정에서 생성자와 판별자의 손실값, MSE, R2 지표 모두 안정적으로 수렴하였다. 이는 모델이 학습을 통해 데이터의 분포를 효과적으로 학습했음을 시사한다.
(2) 학습이 진행될수록 생성된 컬러맵 이미지는 실제 데이터와 점차 유사해졌으며, 학습이 수렴 단계에 도달했을 때 실제 데이터와 매우 높은 유사성을 나타내었다.
(3) 은닉층 수 6, 배치 크기 16, 생성자 입력 차원 2,000의 설정에서 가장 우수한 학습 성능을 나타냈으며, 이는 모델 학습을 위한 최적의 초매개변수 조건으로 평가되었다.
(4) 학습된 생성자를 활용하여 조건 레이블에 따라 컬러맵 이미지를 생성할 수 있었으며, 이를 변형 데이터로 변환함으로써 가열선 위치가 주어졌을 때 강판 변형 크기를 예측할 수 있었다.
(5) 학습된 생성자를 활용한 검증 결과, 제안된 모델이 실제 데이터에 대해 예측한 변형 크기의 상대 오차는 평균 약 3%로 나타났으며, 최대 오차도 7% 이내로 제한되었다. 이는 선상가열 공정에서 제안된 모델이 매우 우수한 변형 예측 성능을 나타냄을 입증한다.
제안된 cGAN 모델은 선상가열 공정에서 가열선 위치에 따른 강판 변형 형상을 예측할 수 있는 효과적인 도구로 활용될 수 있는 가능성을 입증하였다. 다만 본 연구의 결과는 수치해석 기반의 학습 데이터를 활용한 것으로, 향후 실험적 비교 및 추가 검증을 통한 보완이 필요하다.
REFERENCES
- 1.
Lee, J.-S., (2010), Development of knowledge-based method to automatically derive the deformation estimation formula due to line heating, Journal of Welding and Joining, 28(1), 92-99.
10.5781/KWJS.2010.28.1.092
- 2.
Lee, J.-S., (2011), Effect of curvature on deformation caused by thermal plate forming, Journal of Ocean Engineering and Technology, 25(2), 67-72.
10.5574/KSOE.2011.25.2.067
- 3.
Jang, C.-D., Ko, D.-E., Ha, Y.-S., (2008), Simulation of plate deformation due to triangle heating using inherent strain method, Journal of the Society of Naval Architects of Korea, 45(6), 703-709.
10.3744/SNAK.2008.45.6.703
- 4.
Yang, Y.-S., Nguyen, T.-T., Bae, K.-Y., (2010), Prediction of heating line for plate forming in induction heating process using artificial neural network, Journal of Welding and Joining, 28(4), 1-4.
10.5781/KWJS.2010.28.4.001
- 5.
Thinh, N. T., Bae, K.-Y., Yang, Y.-S., (2023), Using a novel cnn model for predicting the induction heating lines to obtain a desired deformed shape of steel plate, International Journal of Precision Engineering and Manufacturing, 24(10), 1781-1791.
10.1007/s12541-023-00844-1
- 6.
Yang, Y.-S, Nguyen, T.-T, Bae, K.-Y., (2023), A study on prediction of heating positions using faster r-cnn in line heating of a steel plate, Journal of the Korean Society of Manufacturing Process Engineers, 22(6), 1-9.
10.14775/ksmpe.2023.22.06.001
- 7.
Yang, Y.-S., Nam, H.-W., Bae, K.-Y., (2024), Selection of heating lines in the line heating process for steel plates using faster r− cnn, International Journal of Precision Engineering and Manufacturing, 25(8), 1713-1723.
10.1007/s12541-024-01041-4
- 8.
Jiang, H., Nie, Z., Yeo, R., Farimani, A.-B., Kara, L.-B., (2021), StressGan: A generative deep learning model for two-dimensional stress distribution prediction, Journal of Applied Mechanics, 88(5), 051005.
10.1115/1.4049805
- 9.
Oh, S.-H., Jin, H.-K., Joe, S.-J., Ki, H.-S., (2021), Prediction of structural deformation of a deck plate using a GAN-based deep learning method, Ocean Engineering, 239(11), 109835.
10.1016/j.oceaneng.2021.109835
- 10.
Yi, J., Chen, Z., Li, D., Li, J., Liu, J., (2023), Conditional generative adversarial network for welding deformation field prediction of butt-welded plates, Journal of Construction Steel Research, 201(5), 107755.
10.1016/j.jcsr.2022.107755
- 11.
- 12.
Yi, M. S., Lee, D. H., Lee, H. H., Paik, J. K., (2020), Direct measurements and numerical predictions of welding-induced initial deformations in a full-scale steel stiffened plate structure, Thin-Walled Structures, 153, 106786.
10.1016/j.tws.2020.106786
- 13.
Masubuchi, K., (2013), Analysis of welded structures: Residual stresses, distortion, and their consequences. Elsevier.
- 14.
- 15.
Biography
- Young Soo Yang
Professor in the Department of Mechanical Engineering, Chonnam National University. His research interests are in manufacturing processes.
- Kang Yul Bae
Professor in the School of Mechatronics Engineering, Gyeongsang National University. His research interests are in manufacturing processes and mechatronics.