ABSTRACT
With rapid growth of the global electric vehicle market, interest in the development of secondary batteries such as lithium batteries is also increasing. Core functional parts of secondary batteries are known to determine the performance of these batteries. Micro cracks, scratches, and markings that may occur during the manufacturing process must be checked in advance. As part of developing an automated inspection system based on machine vision, this study optimized the design of a linear feeder exposed to an environment with a specific operating frequency continuously to transfer parts at a constant supply speed. Resonance can occur when the natural frequency and the operating frequency of the linear feeder are within a similar range. It can negatively affect stable supply and the process of finding good or defective products during subsequent vision tests. In this study, vibration characteristics of the linear feeder were analyzed using mode analysis, frequency response analysis, and finite element analysis. An optimal design plan was derived based on this. After evaluating effects on vibration characteristics for structures in which vibrations or periodic loads such as mass and rails were continuously applied, the shape of the optimal linear feeder was presented using RSM.
-
KEYWORDS: Secondary battery, Machine vision, Linear feeder, Optimal design, Vibration analysis, Response surface methodology
-
KEYWORDS: 이차전지, 머신 비전, 리니어 공급장치, 최적설계, 진동 해석, 반응표면 분석법
NOMENCLATURE
1. 서론
세계적으로 친환경 모빌리티 산업에 대한 요구가 증가함에 따라, 세계 전기차 시장의 수요가 급증하고 있다. BNEF(블룸버그 뉴 에너지 파이낸스)보고서에 따르면 2040년에는 전기차가 신차 판매량의 55%를 차지하고, 전 세계 자동차 5억 5900만대 중 전기차 비중이 33%에 달할 것으로 예측하였다. 이와 관련한 리튬 배터리 등의 이차전지에 대한 관심도 나날이 증가하고 있다. SNE리서치의 조사에 따르면 전기자동차와 에너지저장장치에 탑재되는 리튬이온 전지의 시장 수요량은 2035년에 5.57 TWh 규모로 증가할 전망으로, 2023년 수요량이 994 GWh와 비교하면 현재 시장 수요량 대비 폭발적으로 성장할 것으로 기대된다[
1,
2].
이 중 이차전지 핵심 기능성 부품은 성능을 좌우하는 중요한 요소로, 품질 확보를 위해 제조 과정에서 발생할 수 있는 미세균열(Micro Crack), 스크래치(Scratch), 마킹(Marking) 등의 결함을 사전에 확인해야 한다. 현재 이차전지 기능성 부품은 관능검사 및 샘플검사 등의 전수검사가 이루어지고 있다. 하지만 제품의 효과적인 고품질 대량생산을 위해서는 양품 및 불량품을 식별하는 전수검사를 위한 AI머신 비전 기반의 자동화 검사시스템 개발 및 기술 확보가 요구된다[
3-
5].
본 연구에서는 자동화 검사 시스템 개발의 일환으로, 이차전지 핵심 기능성 부품의 전수검사를 위한 정밀하고 안정적인 이송 및 공급이 가능하도록 리니어 공급장치(Linear Feeder)의 설계 최적화를 진행하였다. 리니어 공급장치는 일정한 공급속도로 부품을 이송하기 위해 지속적으로 특정 운용 주파수의 진동이 가해지는 환경에 노출된다. 특히 리니어 공급장치를 구성하는 구조물의 고유 진동수와 가진 주파수가 유사한 범위에 있으면 공진이 발생할 수 있다. 이는 안정적인 이송 및 공급에도 부정적인 영향을 미칠 뿐만 아니라, 이후 비전검사에서 양품 및 불량품을 식별할 때 부정확한 결과를 초래할 수 있다.
리니어 공급장치가 머신 비전 검사 장비에서 원활하게 부품을 이송할 수 있도록 하기 위해서는, 해당 장치의 운용 주파수와 리니어 공급장치의 주요 부품을 포함한 구조물의 고유 진동수 특성에 대한 설계 최적화가 필요하다. 다양한 최적화 문제를 해결하기 위해 여러 기법이 연구되어 왔으며, 전통적인 수학적, 통계학적 접근법으로는 경사 하강법(Steepest Descent), 순차 이차 계획법(SQP), 다변량 함수 설계(MFD) 등이 대표적이다. 한편, 자연현상을 모사한 메타휴리스틱 기법으로는 유전 알고리즘(GA)과 입자 군집 최적화(PSO) 등이 널리 활용되고 있다. 이 중에서도 실험계획법(DOE)과 통계 기반의 수학적 기법이 결합된 반응표면법(Response Surface Methodology, RSM)은 설계 변수와 응답 간의 관계를 해석적 근사 모형으로 표현함으로써, 제약조건을 포함한 목적함수를 효과적으로 도출할 수 있는 장점이 있다. 특히 계산 효율이 뛰어나 다양한 하중 조건 하에서의 기계 시스템 최적화에 폭넓게 적용되고 있다.
반응표면법 기반 최적설계에 관한 대표적인 연구 사례는 다음과 같다. 장준호 외 4명[
6]은 자동화 용접장치의 회전 시 자중에 의한 유효응력 및 안전율을 주요 최적화 인자로 설정하고, 실험계획법과 반응표면법을 적용하여 구조 최적화를 수행하였다. 소기성 외 3명[
7]은 양항력형 수직축 풍력발전기 블레이드의 파손 여부를 예측하기 위해, 블레이드 응력에 영향을 미치는 설계 인자를 도출하고, 실험계획법 및 반응표면법 기반의 최적 설계를 수행하였다. 예상돈 외 2명[
8]은 압전 액추에이터 기반의 지속 진동을 통해 일정 변위를 전달하는 스테이지 시스템의 유연 힌지를 대상으로, 최대 유효응력과 1차 고유진동수의 극대화를 목표로 설정하여 반응표면법 기반 구조 최적화를 진행하였다. 이들 연구 모두 유한요소해석(FEA)을 활용한 해석 데이터를 기반으로 구축된 반응표면함수를 활용하여 설계 변수에 따른 구조 응답을 정량적으로 분석하였다.
따라서 본 연구에서는 유한요소법을 이용한 모드 해석(Modal Analysis) 및 주파수 응답 해석(Frequency Response Analysis)을 수행하여 리니어 공급 장치의 진동 특성을 정량적으로 평가하였다. 특히, 보조 질량(Mass)과 이송 레일(Supply Rail) 등 주기적 진동 하중이 작용하는 주요 구조물에 대해 진동 응답 특성을 각각 분석하였다. 이후, 실험계획법과 반응표면법을 활용하여 진동 특성에 기반한 최적설계안을 도출하였다. 최종적으로, 최적설계 형상이 설계 목표와 부합하는지를 운용 실험을 통해 검증하였으며, 이를 실제 머신 비전 검사 시스템의 시제품 제작에 적용하여 실효성을 확인하였다.
2. 리니어 공급장치 개요
2.1 리니어 공급장치 초기설계안(Baseline)
본 연구에서는 S사의 AI 머신 비전 검사 시스템 장비에 사용하는 리니어 선형나사 공급장치(H사의 HLFB-02)를 대상으로 최적설계를 수행하였다. 해당 장치는 진동을 이용해 부품을 일정한 속도로 이송하는 기계장치로, 본체의 진동자(Oscillator)가 작동하면 판스프링(Plate Spring)의 탄성에 의해 진동이 이송 레일(Supply Rail)로 전달되며, 이 진동에 의해 부품이 전진 이동하는 구조이다. 머신 비전 검사 시스템에서 운용시 부품의 종류 및 이송속도에 따라 150-180 Hz의 주파수로 작동된다. 본 연구에서는 당사 머신 비전 검사 시스템의 운용 조건에 맞추어 150 Hz를 운용 주파수로 설정하였다.
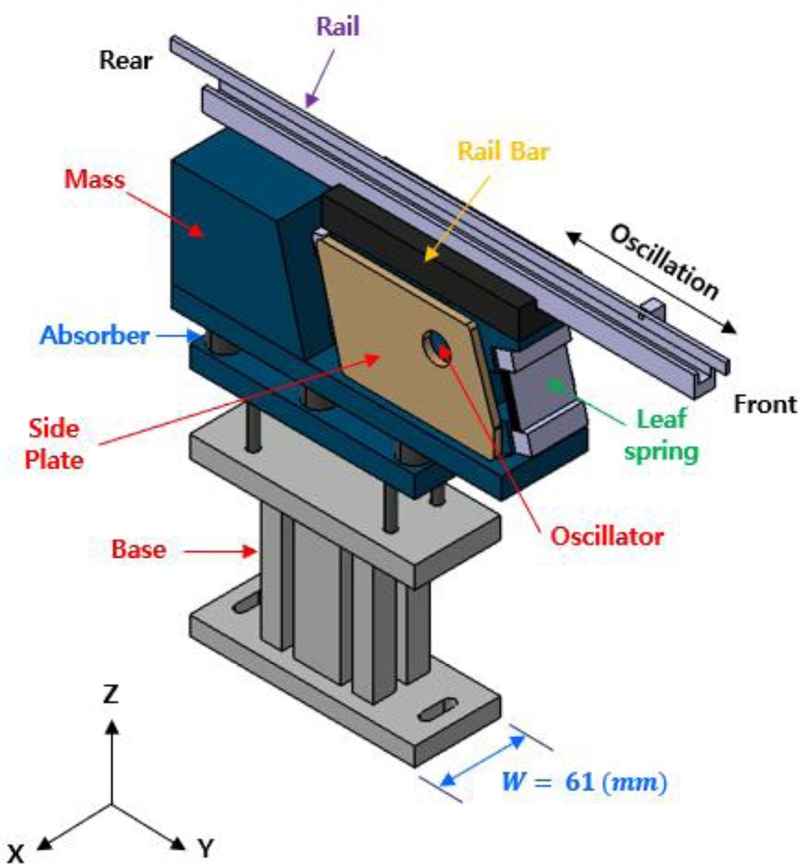
Fig. 1은 리니어 공급장치의 부품 구성도이며,
Table 1은 각 부품에 사용된 재료 물성치를 나타낸다. 이때 장치의 구조적 안정성을 확보하기 위해 Base Frame은 SS41강을 적용하였으며, 진동이 외부 시스템으로 전달되는 것을 저감하기 위해 고무 재질의 Absorber를 Base Frame과 상부 사이에 배치하였다.
Table 1Material properties of the linear feeder components
Table 1
|
Part |
Material |
Elastic modulus [GPa] |
Poisson’s ratio |
Density [kg/m³] |
|
Base, Mass, Oscillator, Side plate |
SS41 |
205 |
0.30 |
7,850 |
|
Rail |
SUS304 |
197 |
0.31 |
8,000 |
|
Rail bar |
AC4B |
71 |
0.33 |
2,950 |
|
Leaf spring |
SK5 |
202 |
0.28 |
7,830 |
|
Absorber |
Rubber |
0.003 |
0.49 |
1,090 |
Fig. 1Structural configuration of the linear feeder
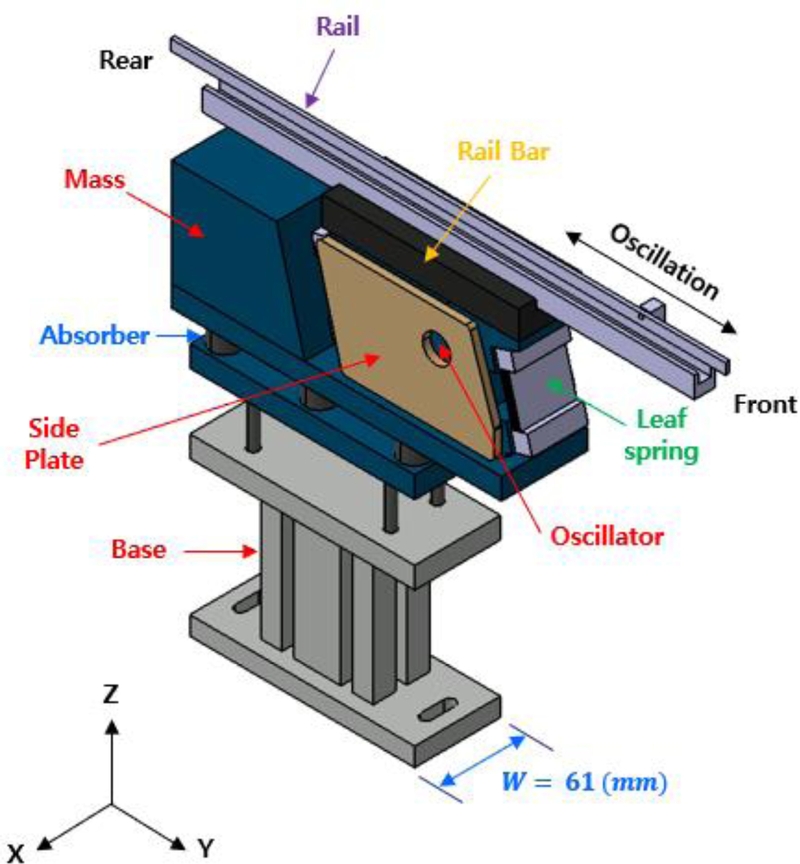
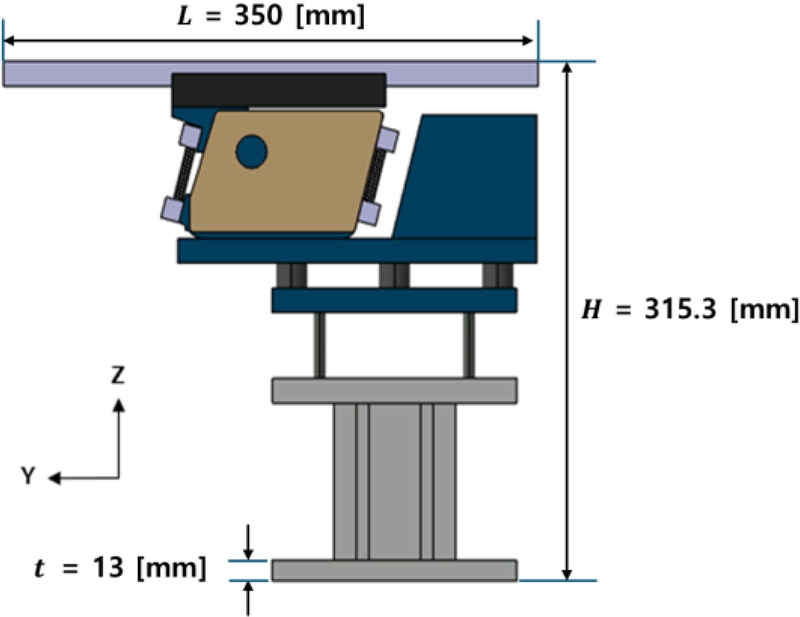
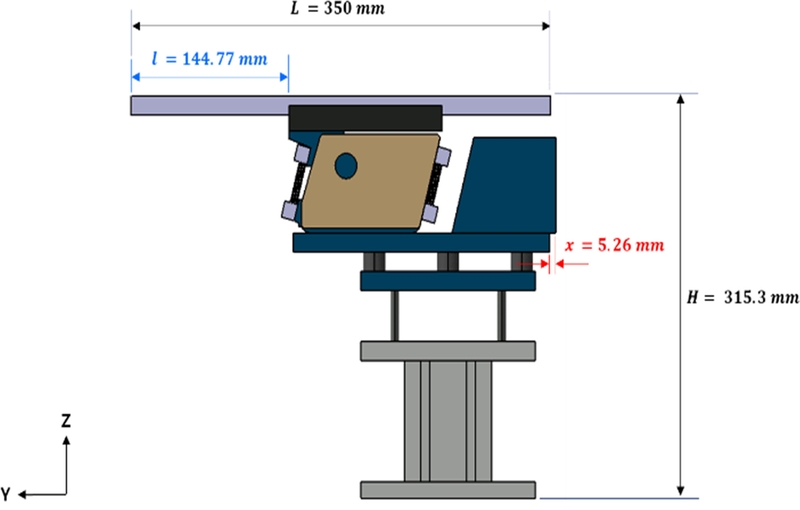
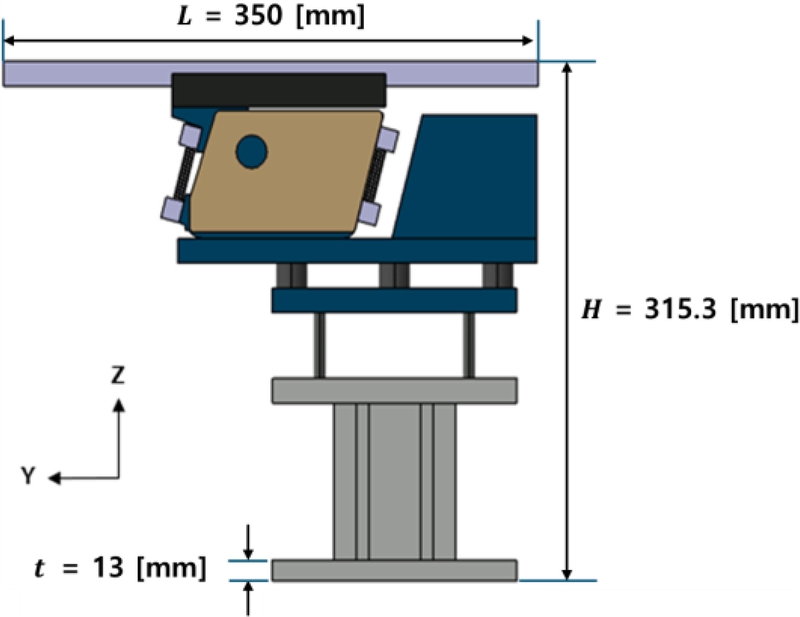
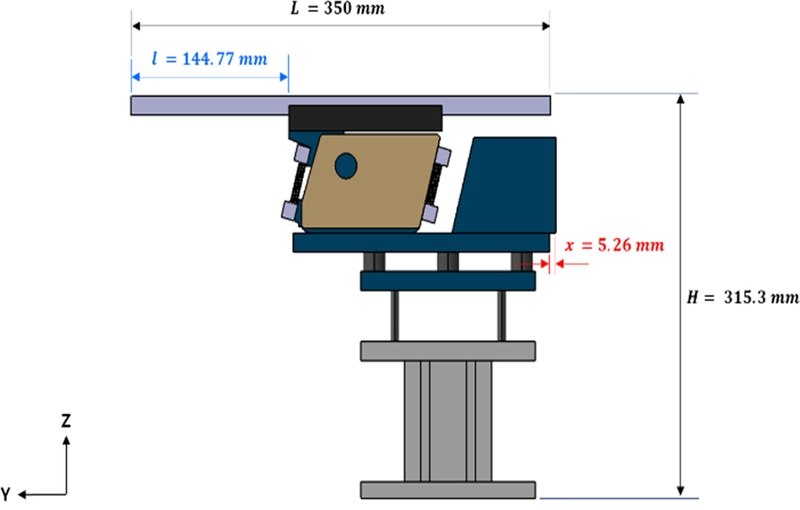
공급장치의 초기 설계안에서는 레일(Rail) 부의 전체 길이(
L)를 350 mm, 장치 전체 높이(H)를 315.3 mm, Base Frame의 두께를 13 mm로 설정하였다. 이를 바탕으로
Fig. 2와 같이 3D CAD 모델을 구성하였으며, 이를 진동 특성 해석에 활용하였다.
Fig. 2Dimensions of the initial design
2.2 설계 변수 및 Case Model 설정
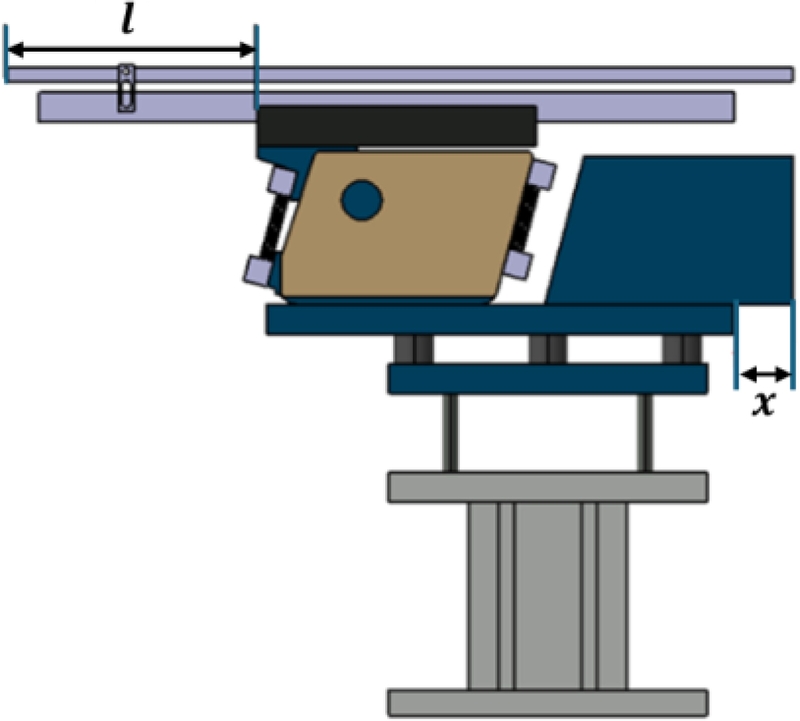
본 연구에서는 선행 연구 결과[
9]를 바탕으로 진동 특성에 주요하게 영향을 미치는 부품의 길이와 위치를 설계 변수로 설정하였다. Rail Bar를 제외한 Rail의 길이는 부품 이송 시 발생하는 마찰에 의해 진동 특성에 직접적인 영향을 미친다. 또한, 보조 질량의 위치를 조정하면 Rail의 공진 정도를 조절할 수 있어, 운용 진동수에 따른 직진 방향 공급 효과를 최적화할 수 있다. 이에 따라,
Fig. 3과 같이 Rail의 길이(
l) 및 보조 질량 위치(
x)를 두 개의 설계 변수로 설정하였다. 또한, 해당 시스템은 기존 머신 비전 검사 장비에 탑재 및 운용되어야 하므로, 장비 크기를 고려하여 최적 설계를 위한 설계 변수의 제한 조건을
Table 2와 같이 정의하였다. 또한, 제한 조건 범위 내에서 각 변수에 대해 10 mm 단위로 총 25가지 Case Model을
Table 3과 같이 정의하였으며, 이를 바탕으로 반응표면법기반 최적 설계를 위한 유한요소해석 데이터를 구성하였다.
Fig. 3Definition of optimal design variables
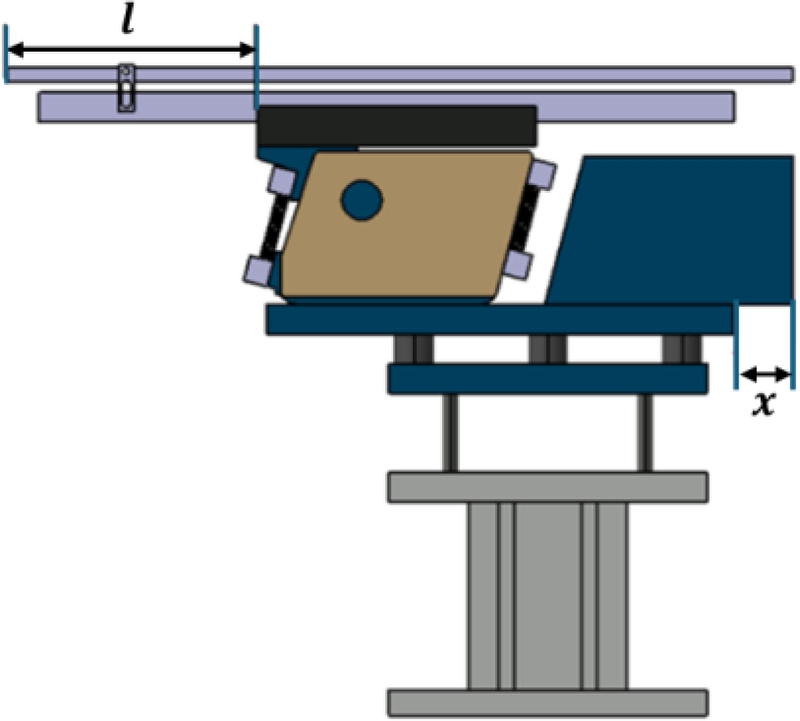
Table 2Design constraints for optimization
Table 2
|
No. |
Design variable |
Condition |
Allowed range |
|
1 |
l (Rail length) |
l ≤ Lmax
|
70 ≤ l ≤ 150 |
|
2 |
x (Mass position) |
x ≤ Xmax
|
-10 ≤ x ≤ 30 |
Table 3Definition of design case models
Table 3
l [mm]
x [mm]
|
70 |
90 |
110 |
130 |
150 |
|
-10 |
Case 01 |
Case 02 |
Case 03 |
Case 04 |
Case 05 |
|
0 |
Case 06 |
Case 07 |
Case 08 |
Case 09 |
Case 10 |
|
10 |
Case 11 |
Case 12 |
Case 13 |
Case 14 |
Case 15 |
|
20 |
Case 16 |
Case 17 |
Case 18 |
Case 19 |
Case 20 |
|
30 |
Case 21 |
Case 22 |
Case 23 |
Case 24 |
Case 25 |
2.3 리니어 공급장치의 유한요소 모델링
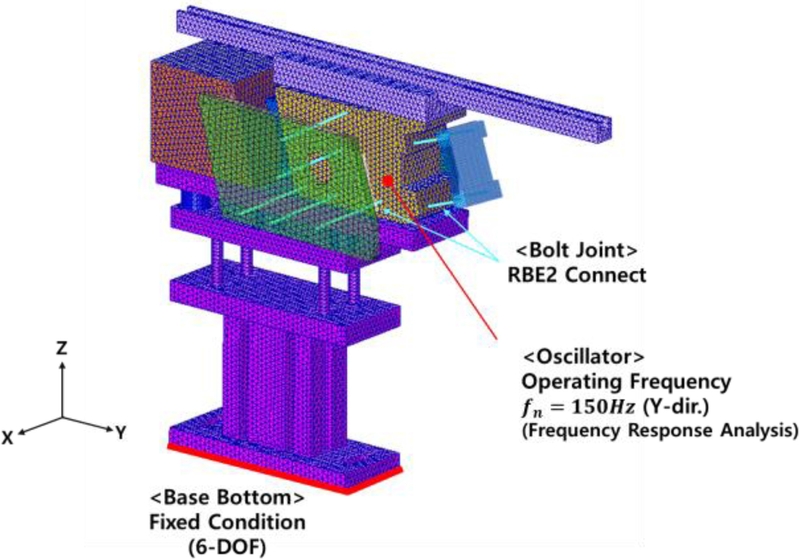
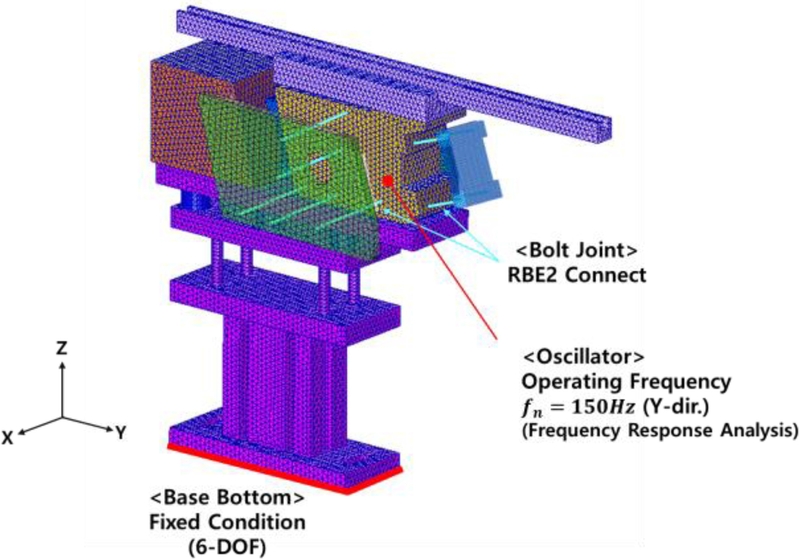
초기 설계안에 대한 유한요소 모델링, 경계/하중 조건 정의 등 전처리 과정을 진행하였고, 이를 바탕으로 25가지의 Case Model에 대한 유한요소 모델링을 수행하였다. 유한요소 모델은 10절점 사면체요소를 사용하여 생성하였고, Side Plate & Leaf Spring 및 Oscillator 간의 볼트 체결부의 경우에는 체결 위치를 확인한 후, 볼트 구조체를 단순화하여 1D 강체요소를 이용하여 모델링 하였다. 전체 모델은 총 321,386개의 절점과 210,608개의 요소로 구성되었다.
리니어 공급장치는 지면에 완전히 고정된 상태에서 Oscillator에서 발생한 약 150Hz의 가진 주파수에 의해 Absorber의 탄성으로 인해 발생한 진동이 Rail로 전달되어 부품을 정렬하여 목표 지점까지 이송하는 원리로 작동한다.
이에 따라,
Fig. 4와 같이 Base 하부의 밑면에 대해 6자유도를 모두 구속하는 경계조건을 적용하였다. 또한, 공급장치는 실제 운용 환경에서는 각 부품 간의 상호작용으로 인해 수직 및 수평 방향의 복합 진동이 발생할 수 있으나, 본 연구의 주파수 응답 해석에서는 해석의 단순화를 위해
Fig. 4의 좌표계 기준으로 주요 진동 방향인 Y축, 즉 수평 방향으로만 가진되는 것으로 가정하여 150 Hz 주파수의 정현파 진동 하중 조건을 부여하였다.
Fig. 4Finite element model of the linear feeder structure
3. 모드해석(Modal Analysis)
3.1 리니어 공급장치의 모드해석
본 연구에서는 모드해석을 통해 리니어 공급 장치 구조물의 고유 진동수와 각 고유 진동수에서 발생하는 모드 형상을 도출하였다. 이를 통해 부품 이송을 위한 주기적인 가진 하중이 작용하는 운용 환경에서의 공진 가능성을 검토하였다. 해석 결과를 바탕으로, 구조물의 고유 진동수가 운용 주파수와 겹치지 않도록 설계하여 공진 현상을 회피할 수 있도록 하였다[
10].
리니어 공급장치는 비전 검사 장비에 탑재되어 Oscillator의 가진에 따라 Rail이 이송 방향으로 진동하고 이로 인해 부품이 이동하는 구조로 구성된다. 부품의 형상과 질량은 종류에 따라 상이하며, 이에 따라 적절한 운용 주파수 범위 역시 달라질 수 있다. 본 연구에서는 검사 시스템에서 주로 취급하는 리벳(Rivet)류 부품을 기준으로 공급장치 구조를 정의하고, 운용 주파수를 150 Hz로 설정하였다.
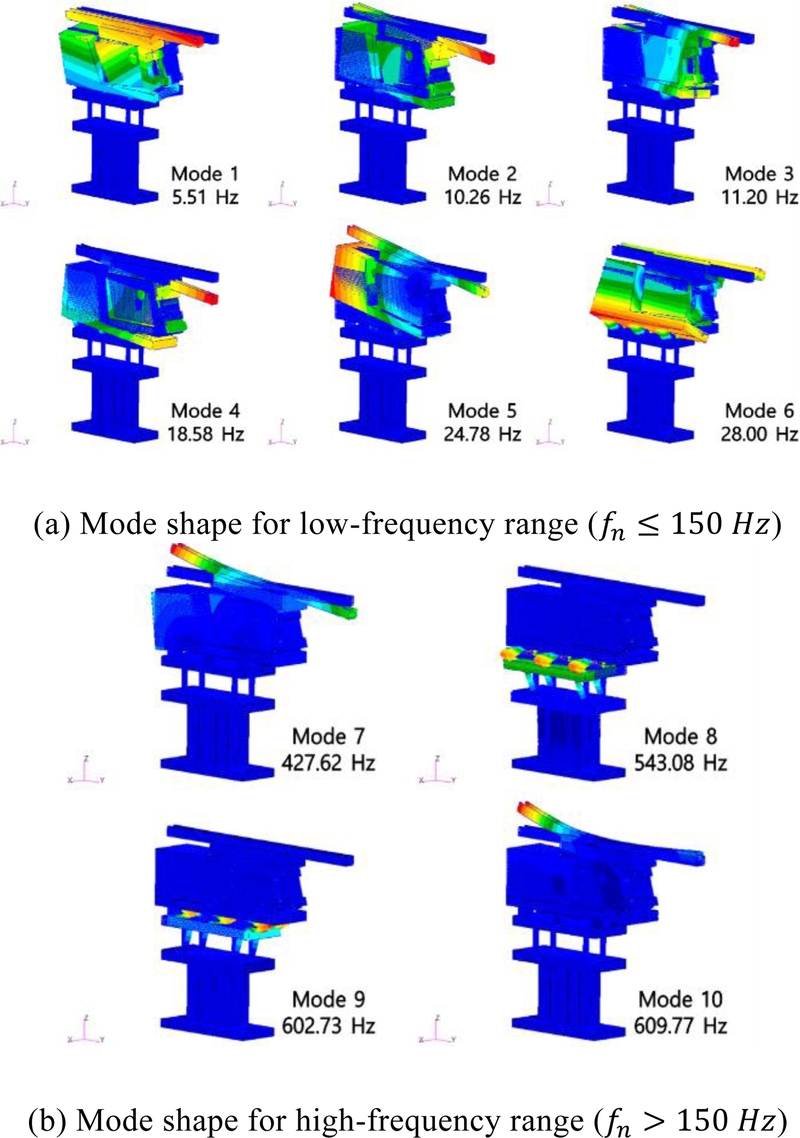
초기설계안(Case 8)에 대한 모드해석 결과는
Fig. 5와 같다. 저차 모드(Mode 1-6)는 고유 진동수가 5-30 Hz 수준으로 운용 주파수보다 낮고, 고차 모드(Mode 7-10)는 고유 진동수가 400 Hz 이상으로 운용 주파수를 충분히 초과하는 특성이 확인되었다. 이는 초기설계안이 공진 위험을 피할 수 있도록 구성되어 있음을 의미한다. 그러나 이송 대상 부품의 다양성을 고려할 경우, 운용 주파수 범위의 확장이 요구된다.
Fig. 5Mode shapes of the baseline linear feeder model
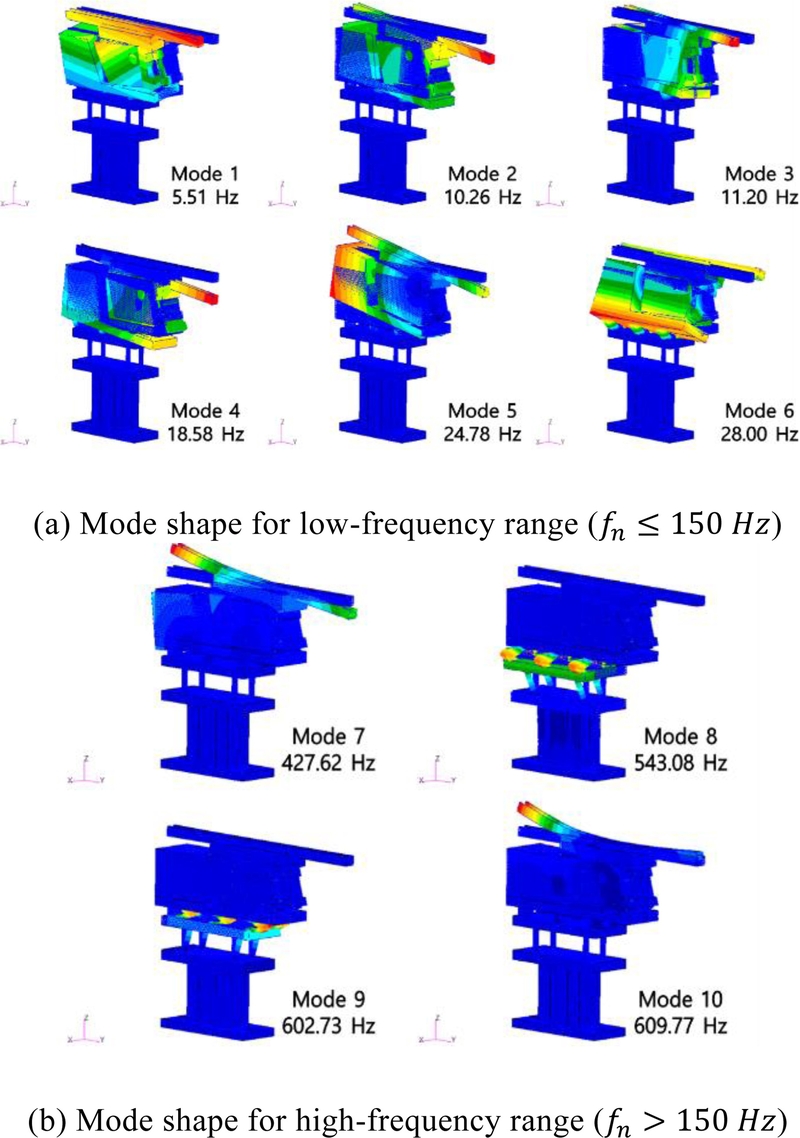
이를 위해서는 고유 진동수가 운용 주파수 범위에 간섭되지 않도록 설계 여유를 더욱 확보해야 하며, 최적설계를 통해 고유 진동수를 운용 주파수로부터 충분히 이격시키는 방향으로 구조 설계를 개선할 필요가 있다[
11].
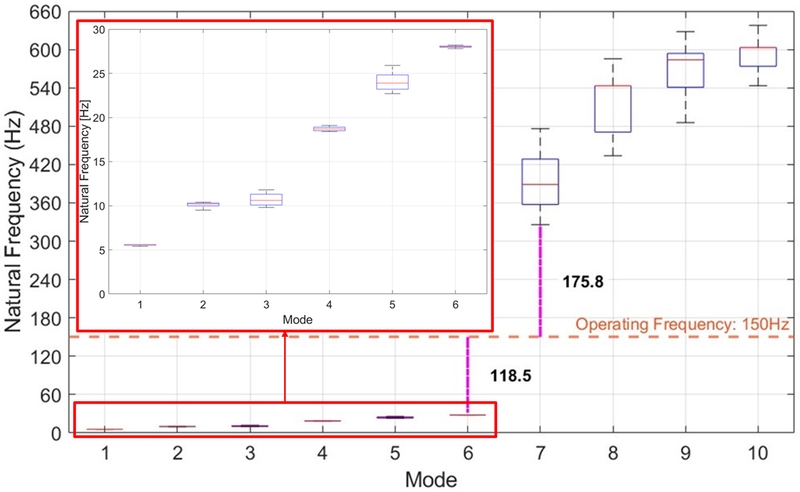
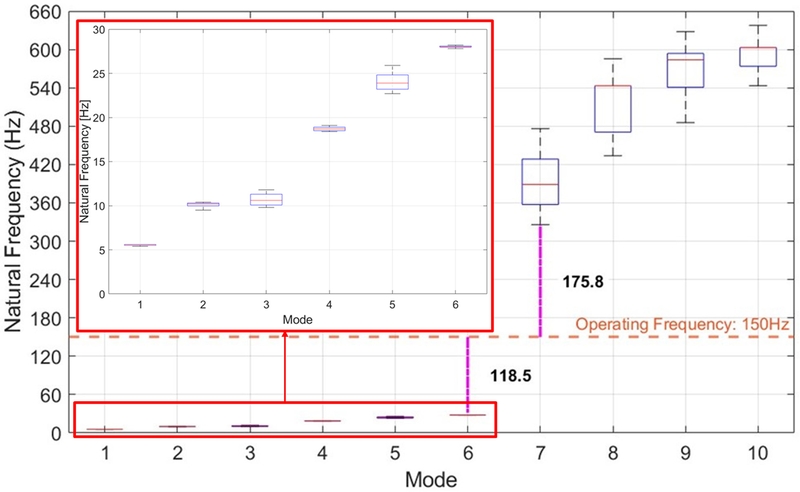
Fig. 6은 주요 설계 변수 조합에 따라 정의된 Case Model들의 모드별 고유 진동수 변화를 나타낸다. 총 25개의 모든 설계안에서 Mode 6과 7 사이에 운용 주파수가 위치함을 확인할 수 있다. 그러나, 다양한 종류의 부품을 안정적으로 이송하기 위해서는 운용 주파수 영역에 인접하는 Mode 6과 7의 고유 진동수를 각각 최소화 또는 최대화하여 활용 가능한 운용 주파수 범위를 더욱 넓힐 필요가 있다. 본 연구에서는 상대적으로 운용 주파수인 150 Hz에 더 가까운 Mode 6의 고유 진동수를 최소화하는 방향으로 최적설계의 목적함수를 설정하였다.
Fig. 6Natural frequency variations for case models
4. 반응표면법 기반 최적설계
4.1 반응표면법
반응표면법은 독립변수와 종속변수 간의 함수 관계를 데이터로부터 추정하여 독립변수의 변화에 따른 반응 값을 예측하는 기법이다. 이를 통해 독립변수의 최적 값을 찾아내고, 데이터 분석을 통해 적합한 반응표면의 성질을 규명할 수 있다[
8].
리니어 공급장치는 일정한 속도로 부품을 이송하기 위해 특정 가진 주파수에서 진동하므로, 구조설계 시 공진 현상을 고려하는 것이 중요하다. 주요 목표는 조물의 고유진동수가 운용 주파수 대역에서 최대한 멀리 떨어뜨리는 것이며, 이를 달성하기 위해 앞에서 설정한 설계 변수 범위에 대한 반응표면법을 적용하였다.
본 연구에서는 두 가지 설계 변수(
k = 2)에 대해 2차 모델로 목적함수를 표현하였으며, 이를 구하기 위해
식(1)과 같은 중심합성계획법(Central Composite Design, CCD)을 사용하였다.
여기서, 매개변수 β는 회귀 계수(Regression Coefficient) 이고, ε는 오차(Error)를 나타낸다. 반응 함수 f(x)는 독립변수 xi에 의해 결정된다.
4.2 반응표면법 기반 최적설계
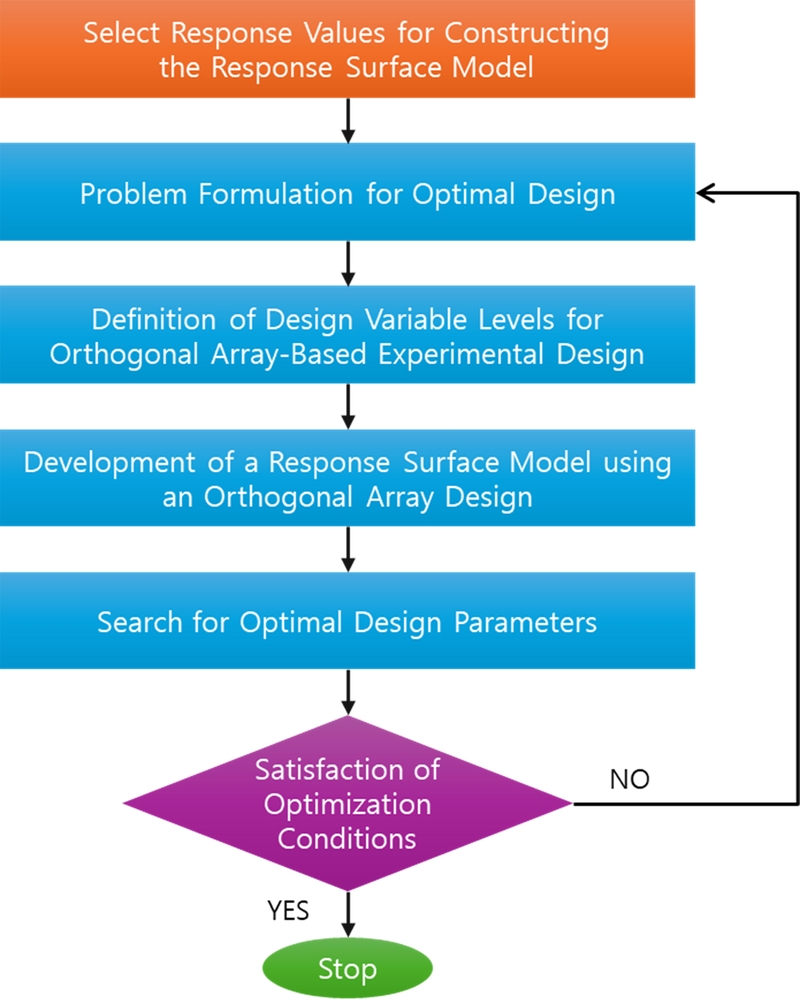
본 연구에서 적용한 반응표면법 기반 최적설계의 방법 및 절차는
Fig. 7과 같다. 먼저, 최적화를 수행하고자 하는 응답변수(출력변수)를 정의하고, 이에 영향을 미치는 입력변수(설계변수)를 선정하였다. 또한, 설계 목적에 부합하는 최적설계 문제를 정식화하고, 중심합성 계획법을 활용하여 설계변수의 가용 범위 내에서 직교배열표(Orthogonal Array)를 구성하였다.
Fig. 7Flow chart of the response surface method
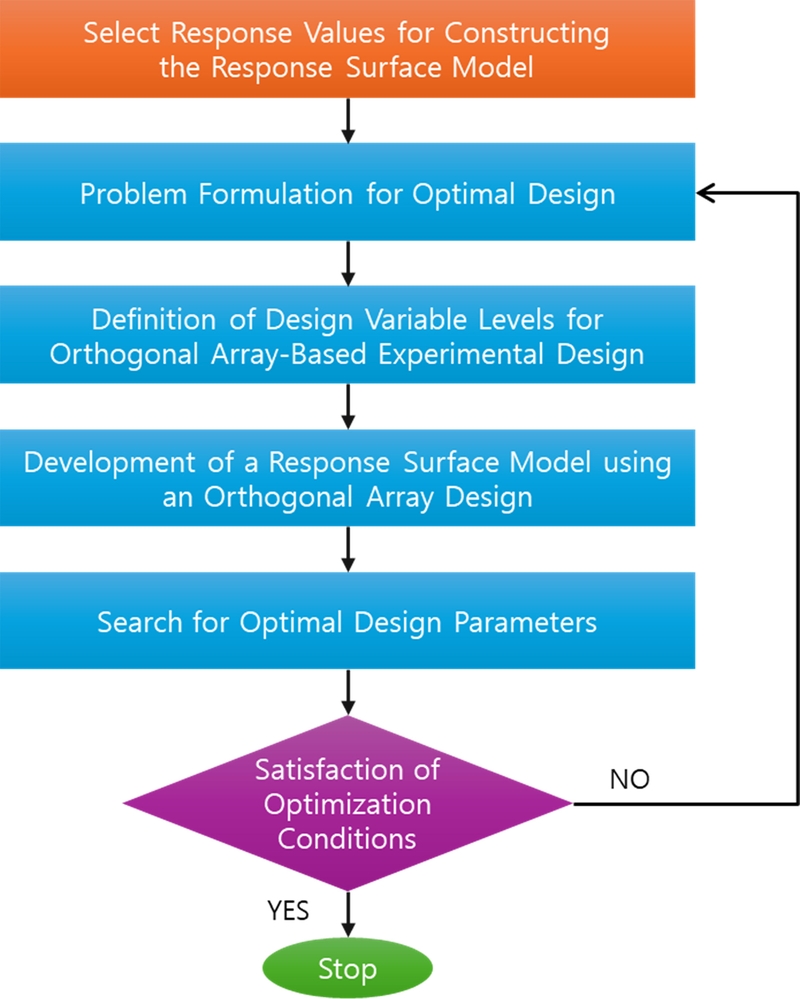
해당 배열에 따라 유한요소해석을 수행하여 실험 응답 데이터를 산출하고, 이를 기반으로 독립변수와 종속변수 간의 수학적 관계를 표현하기 위해 다항 회귀모델 형태의 반응표면함수를 도출하였다. 이때 반응표면함수의 데이터 적합도는 결정계수(Coefficient of Determination, R2)를 활용하여 평가하였다.
이를 통해 정의된 반응표면함수를 바탕으로 설계 목표를 달성할 수 있는 설계 변수의 최적값을 도출하였다. 이때 도출된 최적화 모델에 대해 모드해석을 수행하여 최적설계 결과를 검증하였다. 또한, 주파수 응답 해석을 통해 가진 주파수에서 공급장치의 공진 현상을 검토하였다.
3장에서 수행된 모드해석 결과를 토대로 리니어 공급장치의 Mode 6 고유 진동수를 최소화하기 위하여
식(2)와 같이 최적설계 문제를 정식화하였다.
여기서, X는 설계 변수 x1(질량 위치, Mass position), x2(레일 길이, Rail length)를 의미하며, M과 K는 각각 설계변수에 따라 변하는 공급장치 구조물의 등가 질량(Equivalent Mass)과 강성(Stiffness)을 뜻한다.
또한, 설계 변수 조합에 따른 고유 진동수 응답에 대한 반응표면함수 생성을 위하여
Table 4와 같이 직교배열표를 작성하였다. 본 연구에서는 두 개의 설계변수(
x1,
x2)에 대한 각각 5수준으로 모두 25번의 실험을 진행하여야 하지만, 중심합성계획법을 기반으로 유한요소해석 모델의 생성 시간 단축과 해석 시간 단축을 위한 효율성을 고려하여 확장형 중심합성 계획법(Costomized CCD)을 사용하여 직교배열표를 작성하였다. 이때, 2개 요인에 대한 각 5개의 수준을 같은 개수로 분배하여 균형성을 확보하였고, 직교성을 확보하기 위해 각 수준이 독립적 인가를 고려하여 중심점을 기준으로 실험점의 개수는 4개, 축 점의 개수는 4개, 그리고 중심점 5개에서 총 13개의 실험점을 구성하였다.
Table 4Orthogonal array by modal analysis
Table 4
|
Case |
Mass position (x) [mm] |
Rail length (l) [mm] |
Natural frequency [Hz] |
|
1 |
-10 |
70 |
31.5 |
|
2 |
-10 |
110 |
28.1 |
|
3 |
-10 |
150 |
27.9 |
|
4 |
0 |
110 |
28.0 |
|
5 |
10 |
70 |
28.1 |
|
6 |
10 |
90 |
28.0 |
|
7 |
10 |
110 |
28.0 |
|
8 |
10 |
130 |
28.0 |
|
9 |
10 |
150 |
27.8 |
|
10 |
20 |
130 |
28.0 |
|
11 |
30 |
70 |
28.1 |
|
12 |
30 |
110 |
28.0 |
|
13 |
30 |
150 |
27.9 |
이를 통해 반응표면법을 적용한 결과, 전체 설계 변수를 포함한 경우와 유효 변수만을 고려한 경우 각각의 목적함수 회귀 계수를 도출하였으며, 이를 바탕으로
식(3)과 같이 2차 회귀 방정식 형태의 최적 목적함수를 도출하였다.
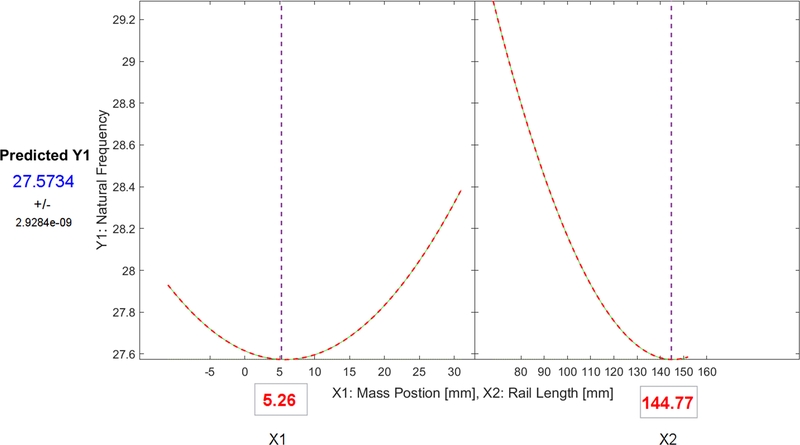
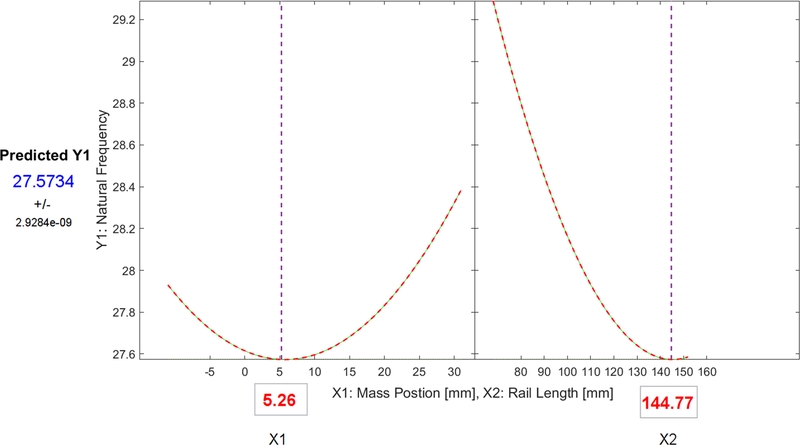
도출된 목적함수를 기반으로 최적설계 조건에 부합하는 최적화설계 변수 값과 그에 따른 고유 진동수 예측값을 탐색하였다. 이때 고유 진동수의 가중치를 1로 설정하여
Fig. 8과 같이 최적화된 설계 변수 값을 도출하였다.
Fig. 8Predicted response trace plots with optimal design value
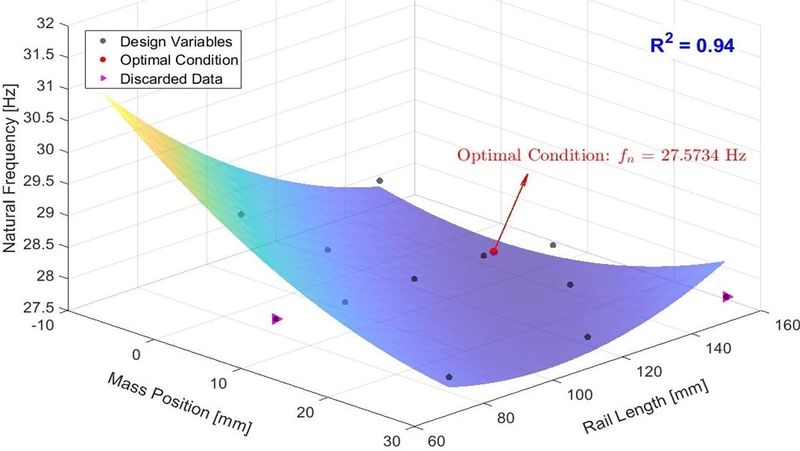
또한, 반응표면함수의 3차원 형상과 최적설계 지점을
Fig. 9와 같이 나타내었다. 이때, 추정된 반응표면함수의 결정계수는 94.48%로 나타났다. 이는 반응표면함수의 설명력에 크게 기여하지 않는 변수들, 즉 최적값에서 거리가 먼 Case 5와 13의 데이터를 제외하고 계산된 결과이다. 이를 통해 반응표면법을 통한 예측 모델은 설계변수에 따른 특성을 효과적으로 나타내는 것으로 확인되었다.
Fig. 9Response surface plot for the predicted natural frequency
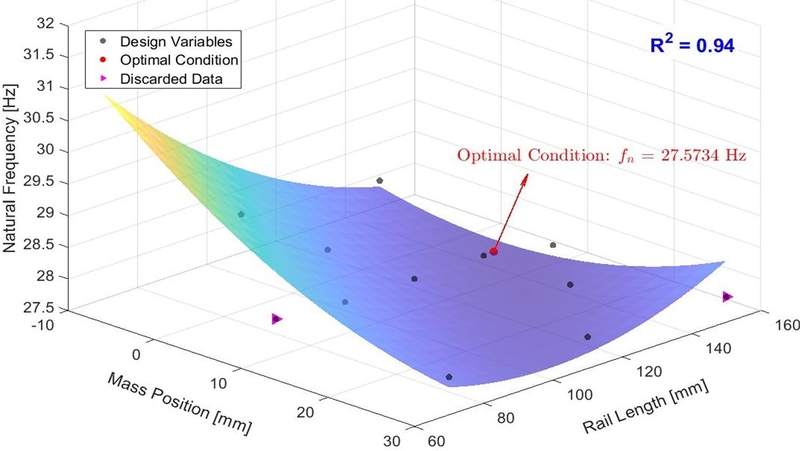
최적화 결과, 보조 질량 위치 x = 5.26 mm, 레일 길이 l = 144.77 mm에서 공급장치의 Mode 6 고유 진동수(fn)는 27.57 Hz로 예측되었다. 이는 초기 설계안 대비 약 1.6% 감소한 수치이며, 공진 회피를 위한 설계 목적에 부합한다. 또한, 예측 모델의 신뢰도를 검증하기 위해 동일 조건에 대해 유한요소 기반 모드해석을 수행한 결과, Mode 6의 고유 진동수는 27.92 Hz로 나타났으며, 예측값과의 차이는 약 1.3%로 오차 범위 2% 이내를 만족하였다.
따라서, 반응표면법을 기반으로 도출된 최적설계 결과는 운용 주파수에서 공진 가능성을 줄이는 설계 목적을 충족하며, 공급장치가 부품 이송을 위한 진동 환경에서 보다 안정적으로 구조적 성능을 확보할 수 있음을 의미한다. 이러한 결과를 바탕으로,
Fig. 10과 같이 최적설계안을 반영한 3D CAD 형상 설계 및 모델링을 수행하였다.
Fig. 10Optimized design model of the linear feeder
4.3 주파수 응답해석(Frequency Response Analysis)
모드 해석을 기반으로 반응표면법 최적화를 수행한 후, 도출된 최적 설계안을 바탕으로 공급장치의 동적 응답 특성을 정량적으로 평가하고자 주파수 응답 해석을 추가로 수행하였다. 공급장치는 주기적인 가진 하중을 받는 구조적 특성상, 특정 주파수에서의 응답 성능을 사전에 파악하는 것이 필수적이다. 따라서, 주파수 응답 해석을 통해 주파수 영역별 공급장치의 동적 특성을 분석하고, 응답(변위)의 Peak 값을 확인하여 최적설계안의 공진 발생 가능성을 평가하였다[
12].
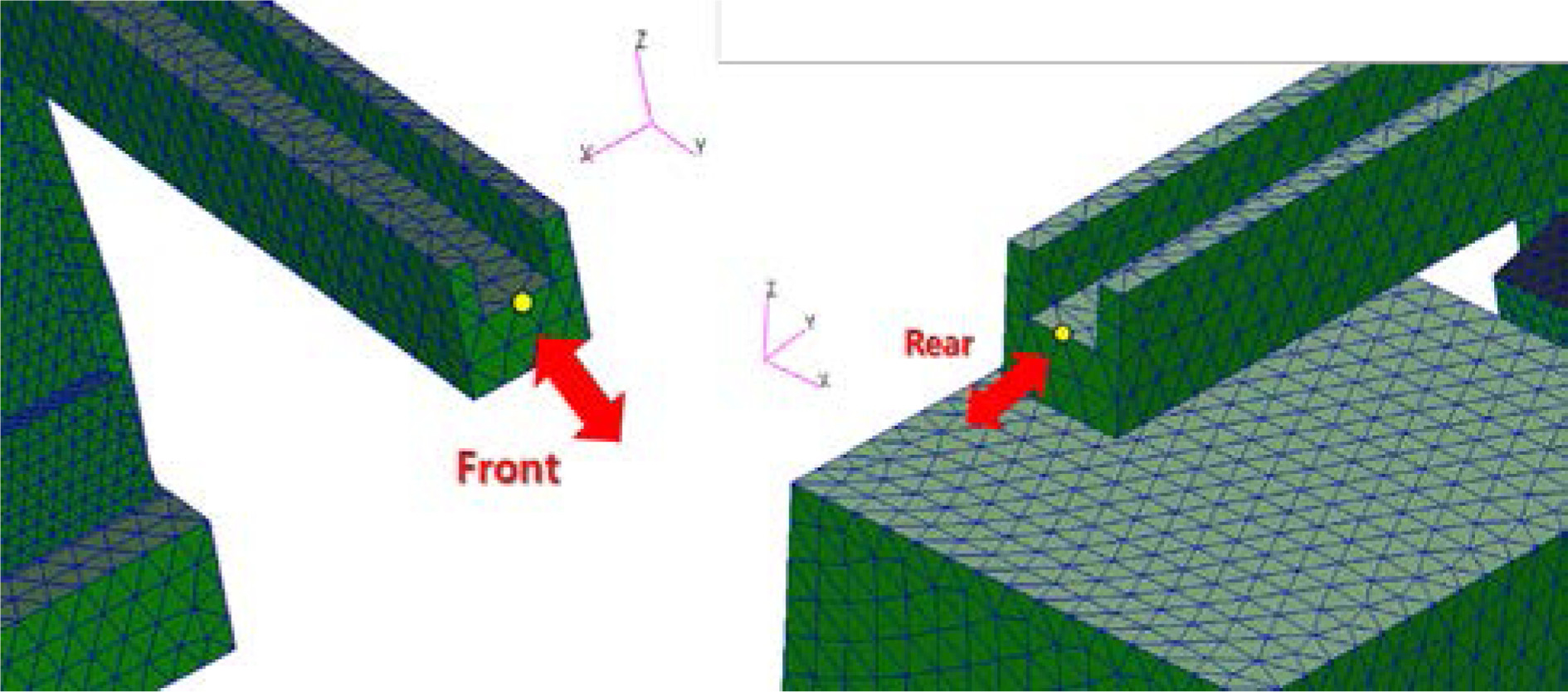
특히, 부품 이송에 직접적인 영향을 미치는 Rail 구조물의 전/후방 끝단에서 공진 주파수에서 발생하는 응답 데이터를 추출하여 공진 시 변위 특성을 분석하였다.
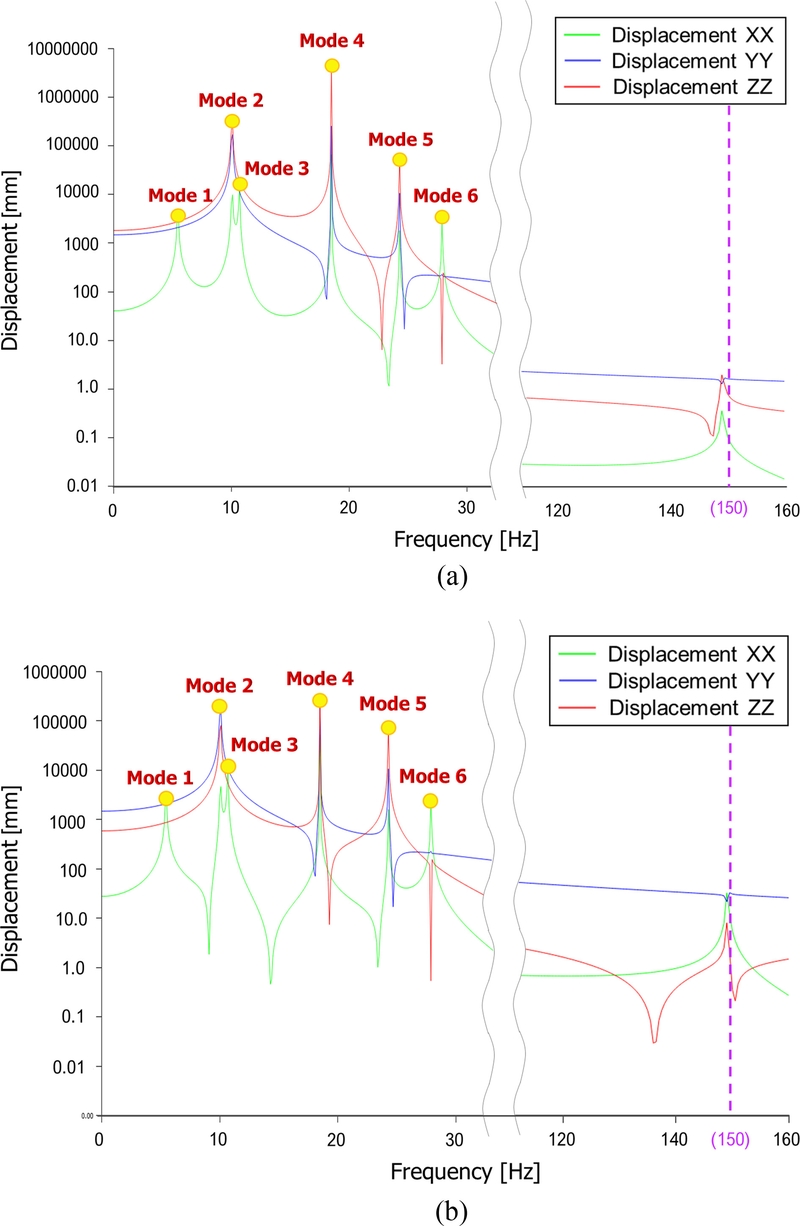
Fig. 11은 Rail 전/후방 끝단의 중앙 절점 위치를 나타내며,
Figs. 12(a)와 12(b)는 해당 위치에서의 주파수에 따른 변위 특성을 나타낸다.
Fig. 11Locations for displacement extraction in frequency response analysis
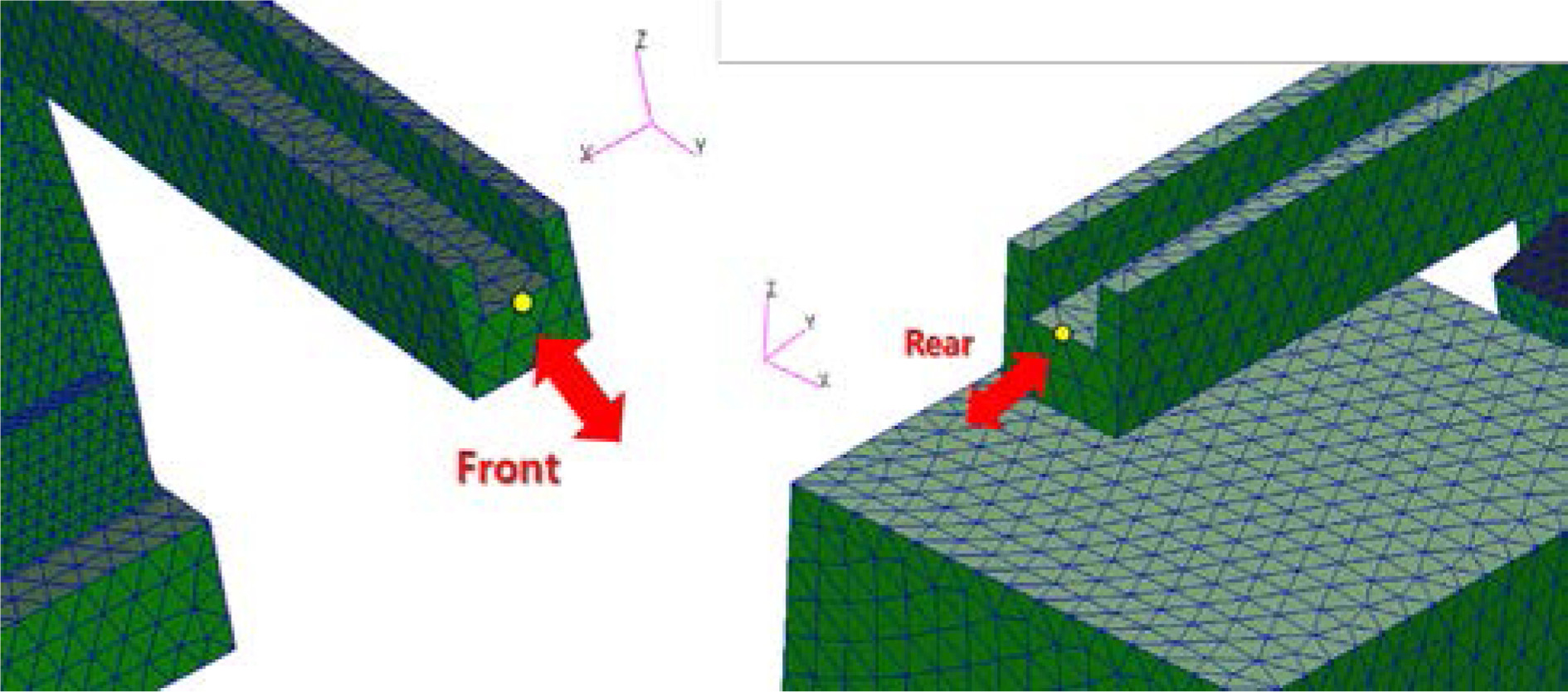
Fig. 12Frequency response analysis results
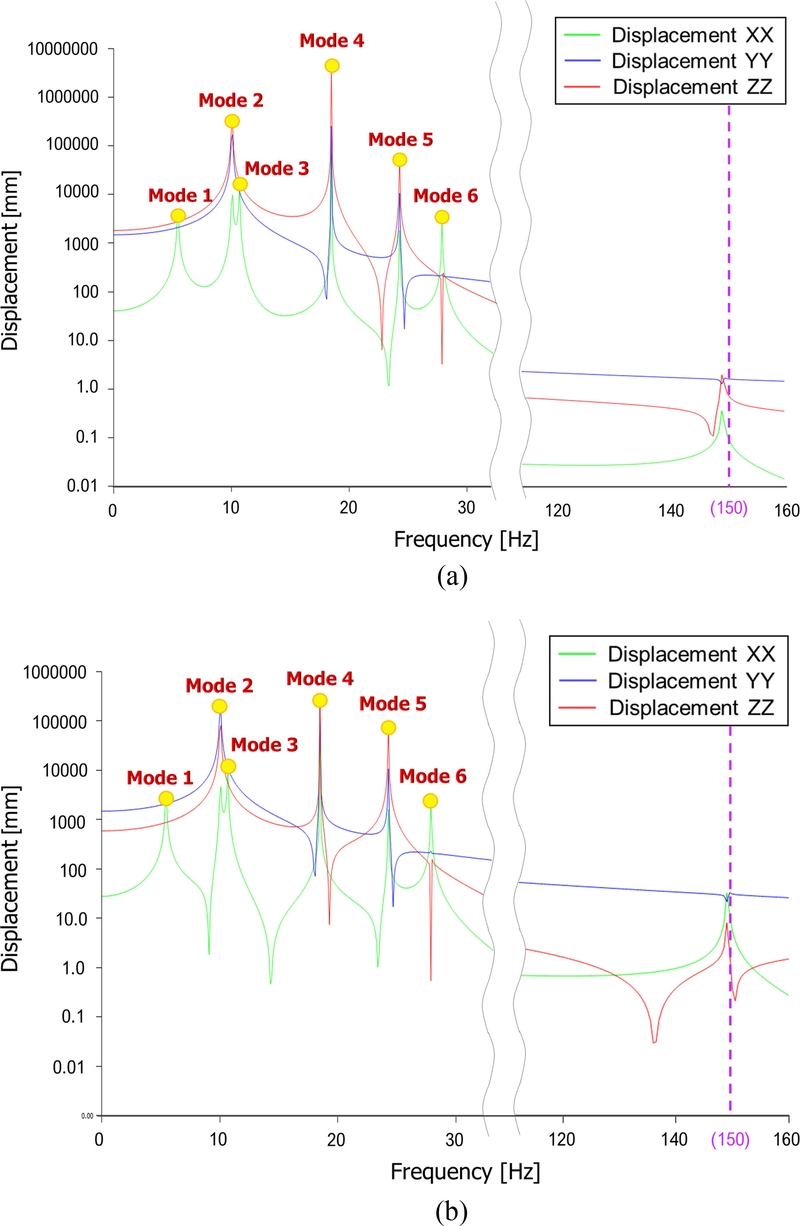
Table 5는 운용주파수와 가장 근접한 진동 모드인 Mode 6에서의 방향별 변위값을 나타낸 것이다.
Fig. 5(a)에 제시된 Mode 6의 모드 형상에서와 같이 X축 방향 진동의 영향이 가장 크게 나타남을 확인할 수 있다. 실제로, X축 방향의 변위가 Y축 및 Z축보다 현저히 큰 값을 보이며, 이를 통해 Rail의 전/후방 모두에서 X축 방향 진동에 의한 공진이 발생했음을 확인할 수 있다. 이러한 결과는 최적설계안에서 예측된 Mode 6의 고유 진동수에서 공진이 발생했음을 의미하며, 결과적으로 최적설계안에서의 고유 진동수 예측값은 실제 진동 특성과 잘 부합함을 알 수 있다.
Table 5Displacement response of mode 6 from frequency response analysis
Table 5
|
Direction |
Rail front [mm] |
Rail rear [mm] |
|
X |
2705.52 |
2336.95 |
|
Y |
227.73 |
227.73 |
|
Z |
3.23 |
0.53 |
한편, 부품 이송 방향인 Y축에 비해 Z축 방향의 변위는 거의 발생하지 않는 것으로 나타났으며, 이는 레일 구조물의 전/후방에서 수직 방향(Z축)의 튐 현상이 발생하지 않았음을 의미한다.
Fig. 12에서 확인할 수 있듯이, 운용 주파수인 150 Hz 부근에서 Z축 변위가 약 9 mm 정도 발생하였다.
그러나 해당 변위는 저차 고유 진동수에서 발생하는 변위에 비해 현저히 낮은 수준으로, 부품 이송에 영향을 주는 과도한 진동이라 판단되지 않는다. 따라서, 운용 주파수 영역에서 공급장치의 동적 안정성이 충분히 확보됨을 확인할 수 있었다. 이를 통해 공급장치의 레일 부에서의 공진 가능성을 평가하고, 최적설계안의 고유 진동수 특성을 확인 및 검증하였다.
4.4 최적설계 모델 시제품 제작
초기 설계안에 대한 진동 특성 해석과 반응표면법을 활용하여 리니어 공급장치의 최적 설계를 수행하였다. 이를 바탕으로과
Fig. 13같이 리니어 공급장치의 시제품을 제작하였으며, 실제 검사장비에 적용하기 위해 초기 설계 목표에 부합하는지에 대한 성능평가를 진행하였다. 성능 평가는 측정 시료의 단위 개수를 투입한 후 경과 시간을 측정하고, 이를 초당 공급 속도로 환산하여 60분 기준의 생산량을 산출하는 방식으로 수행되었다. 측정 결과와 목표 충족 여부는
Table 6에 정리하였다.
Fig. 13Prototype of the optimized linear feeder

Table 6Elapsed time measurement results
Table 6
|
Performance metrics |
Test Target |
Result |
Status |
|
Supply rate [ea./sec] |
5 |
5 |
Satisfied |
5. 결론
본 연구는 유한요소해석(FEA)을 기반으로 AI 검사 장비용 리니어 공급장치의 최적설계를 수행하고, 이를 바탕으로 실제 시제품을 개발하였다. 설계의 주요 목표는 검사 시스템에서의 안정적인 부품 이송과 결함 검사의 정밀도를 확보하는 데 있다.
우선, 초기 설계안에 대한 모드해석을 통하여 진동 특성을 분석하고, 운용 주파수(약 150 Hz) 부근에서의 공진 가능성을 평가하였다. 초기 구조는 고유진동수가 운용 주파수와 충분히 이격되도록 설계되었으나, 보다 높은 이송 안정성과 다양한 부품에 대한 운용 확장성을 확보하기 위해 반응표면법을 적용하여 최적화 설계를 수행하였다.
최적설계를 통해 도출된 설계 변수는 고유진동수를 약 1.6% 낮추는 효과를 보였으며, 이를 통해 공진 발생 가능성을 보다 효과적으로 억제할 수 있었다. 이때 반응표면법 기반 최적설계를 통해 예측된 고유 진동수와 유한요소해석 결과 간의 비교를 통해 예측 모델에 대한 적합성을 검증하였다.
또한, 주파수 응답 해석을 수행하여 최적설계안에 대한 구조적 응답을 검증하였고, 특히 Rail 전/후방 끝단의 주파수에 따른 변위 응답 분석을 통해 공진 발생시 변위 특성과 운용 주파수에서의 공진 발생 가능성이 낮음을 확인하였다.
마지막으로, 본 연구에서 도출된 최적설계안을 기반으로 리니어 공급장치의 시제품을 제작하고 성능 평가를 수행하였다. 그 결과, 초기 설계 목표를 만족하는 안정적인 부품 이송 성능을 확보할 수 있었다. 이를 통해 제안된 설계 및 해석 기법의 실효성과 현장 적용 가능성이 입증되었다.
ACKNOWLEDGMENTS
본 연구(결과물)는 교육부와 한국연구재단의 재원으로 지원을 받아 수행된 3단계 산학연협력 선도대학 육성 사업(LINC 3.0)의 연구 결과입니다.
REFERENCES
- 1.
- 2.
- 3.
- 4.
LEE, G. J., (2020), Automatic inspection system for secondary battery separators using deep learning-based AI technology, KR20210106038.
- 5.
- 6.
Jang, J.-H., Lee, D.-S., Jung, W.-J., Jung, S.-H.,Jung, J.-S., (2013), The structure optimization research of the automation welding equipment of the large l-type using the response surface method, Journal of the Korean Society of Manufacturing Technology Engineers, 22(1), 138-144.
10.7735/ksmte.2013.22.1.138
- 7.
So, K.-S., Choi, C.-W., Lee, D.-C., Kang, K.-W., (2013), Structural optimization for hybrid vertical-axis wind turbine blade using response surface method, Transactions of the Korean Society of Mechanical Engineers A, 37(11), 1331-1337.
10.3795/KSME-A.2013.37.11.1331
- 8.
Ye, S.-D., Min, B.-H., Lee, J.-K., (2006), Design of ultra-precision micro stage using response surface methodology, Journal of the Korean Society of Manufacturing Process Engineers, 5(1), 39-44.
- 9.
Seo, Y.-R., Park, K., Kim, S.-K., Ra, S.-W., (2011), Vibration analysis for a feeding unit of vision inspection system of precision screws, Journal of the Korean Society of Manufacturing Technology Engineers, 20(4), 446-451.
- 10.
- 11.
Lee, J.-M., Yu, H.-T., Park, G.-J., Choi, H.-C., Choi, B.-K., (2015), Design for resonance avoidance of mount through the modal analysis, Transactions of the Korean Society for Noise and Vibration Engineering, 25(7), 481-486.
10.5050/KSNVE.2015.25.7.481
- 12.
Lee, K.-H., Kim, S.-H., Chung, J.-T., (2007), Design and analysis of a linear feeder using computer simulation, Proceedings of the Korean Society for Noise and Vibration Engineering Conference, 749-753.
Biography
- Jeong Ho Han
B.S.E candidate in the Department of Aeronautical and Mechanical Design Engineering, Korea National University of Transportation. His research interests are advanced analysis and metallic & composite structural design.
- Jun Beom Bang
B.S.E candidate in the Department of Aeronautical and Mechanical Design Engineering, Korea National University of Transportation. His research interests are advanced analysis and metallic & composite structural design.
- Seung Woo Ra
Professor in the Creative Convergence Division and Director of the industry and academia cooperation support center, Korea National University of Transportation. His research interests are composite material design, vision inspection and smart factory.
- Joon Hwang
Professor in the Dept. of Aeronautical and Mechanical Design Engineering, Korea Nat’l Univ. of Transportation and Director of National Key Technology Institute in University of NRF Korea. His research focuses on AI based multimodal system design.
- Myung Jun Kim
Professor in the Department of Aeronautical and Mechanical Design Engineering, Korea National University of Transportation. His research interests are structural analysis and design optimization.
- Gyu Hun Lee
President in SmartVisionTech. His research interests are machine vision inspection systems, smart camera, and smart factory.