ABSTRACT
Overhang structures are essential geometries in metal additive manufacturing for realizing complex shapes. However, achieving stable, support-free overhang structures requires precise control of process parameters, and securing shape fidelity becomes particularly challenging as overhang length increases due to thermal deformation. To address this challenge, this study proposed a Bayesian optimization framework for efficiently identifying optimal process parameters to fabricate high-difficulty overhang structures. An image-based scoring method was developed to quantitatively evaluate shape defects. Experimental data were collected by fabricating 3, 6, and 9 mm overhang structures with various process parameters. Based on collected data, Gaussian Process Regression (GPR) models were trained. A physics-informed soft penalty term based on energy density was incorporated to construct a surrogate model capable of making physically plausible predictions even in extrapolated regions. Using this model, Bayesian optimization was applied to overhang lengths of 12, 15, and 18 mm, for which no prior experimental data existed. Recommended parameters enabled stable, support-free fabrication of overhang structures. This study demonstrates that reliable optimization of process parameters for complex geometries can be achieved by combining minimal experimental data with physics-informed modeling, highlighting the framework’s potential extension to a wider range of geometries and processes.
-
KEYWORDS: Laser powder bed fusion, Overhang structure, Bayesian optimization, Process parameter optimization
-
KEYWORDS: 레이저 분말 베드 융합, 돌출 구조, 베이지안 최적화, 공정변수 최적화
NOMENCLATURE
Linear Energy Density (P/V)
1. 서론
적층 제조(Additive Manufacturing)는 3차원 모델링 데이터를 기반으로 소재를 적층하여 복잡한 형상을 구현하는 공정으로서 높은 설계 자유도와 맞춤형 생산에 적합하다는 장점으로 인해 최근 다양한 산업 분야에서 주목받고 있다. 그중에서도 Laser Powder Bed Fusion (L-PBF)은 금속 분말을 베드 위에 균일하게 도포한 후, 고출력 레이저를 이용해 선택적으로 용융시켜 적층하는 방식으로서 상대적으로 높은 해상도와 치수 정밀도를 제공하는 공정이다. L-PBF는 별도의 후가공 없이 기존 제조 방식으로 구현이 어려운 내부 채널이나 미세 격자 구조를 단일 공정으로 정밀 제작할 수 있는 장점을 지닌다[
1]. 이와 같은 형상 구현 능력은 항공, 우주, 의료, 에너지 등 다양한 산업 분야에서 기능성 구조체의 제작에 활용되고 있으며[
2], 대표적인 예로는 내부 냉각 채널, 공진기 구조, 에너지 흡수용 격자 구조 등이 있다[
3,
4].
이들 구조는 출력 중 하부에 지지 구조가 없는 오버행(Overhang) 형상을 필연적으로 포함한다. 오버행 형상은 출력층 아래에 용융된 금속이 아닌 분말만 존재하여 열전달이 제한되는 구조로, 뒤틀림(Warping), 잔류물(Dross) 형성, 거친 표면 등의 결함이 발생한다[
5]. 반대로, 스캔 속도를 높여 에너지 밀도가 감소할 경우, 팽창(Swelling) 결함이 발생할 수 있다[
6]. 일반적으로 경사각이 45° 이하인 경우 목표 형상 구현이 어려워, 지지 구조의 설치가 요구되며 지지 구조는 안정성과 열전달 경로를 제공하는 역할을 한다. 하지만 밀폐된 내부 구조처럼 물리적으로 지지 구조를 설치할 수 없는 경우도 있으며, 설치가 가능하더라도 적층 공정 완료 후 제거가 필요하고, 구조가 복잡할수록 제거가 어려워 부품 손상으로 이어질 수 있다[
7]. 이러한 이유로 지지 구조 없이도 안정적인 형상 구현이 가능한 공정 조건의 탐색이 중요한 과제로 떠오르고 있으며, 이를 위해 레이저 파워, 스캔 속도, 스캔 간격, 층 두께 등 다양한 공정 변수를 정밀하게 조절해야 한다. 이들 변수는 서로 비선형적인 상호작용을 통해 출력 형상에 영향을 미치므로 반복 실험을 통한 최적화가 필요하며, 이는 장비 세팅, 분말 도포, 냉각, 후처리 등 많은 시간과 비용이 수반되는 L-PBF 공정의 특성상 비효율적이다.
반복적 실험 기반 접근의 시간적·비용적 부담을 완화하기 위해 다양한 연구가 수행되어 왔다. 통계적 실험 설계를 통해 공정 변수와 품질 간의 상관성을 정량적으로 분석하거나[
8], 열해석 시뮬레이션을 활용하여 열 축적을 예측하고 지지 구조를 최적화하려는 시도가 이어져 왔다[
9,
10]. 최근에는 인공지능(Artificial Intelligence, AI) 기법이 도입되어, 공정 중 수집된 열화상 데이터를 기반으로 결함 발생 여부를 예측하거나[
11], 시뮬레이션 데이터를 활용해 용융풀(Melt Pool) 거동을 추정하는데 활용하고 있다[
12]. 이처럼 AI 기반 접근은 결함 감지, 형상 예측 공정 이상 진단 등에 활용되고 있으나, 최적 공정 변수의 사전 탐색과 관련해서는 제한적으로 다뤄지고 있다. 이러한 배경에서, 베이지안 최적화(Bayesian Optimization)는 고비용 공정에서의 효율적인 공정 변수 탐색을 위한 유망한 접근법으로 주목받고 있으며, 이 기법은 최소한의 실험만으로도 최적 조건을 도출할 수 있는 확률 기반의 최적화 기법이다[
13]. 실제로 화학 공정, 재료 설계, 머신 러닝 하이퍼파라미터 튜닝(Hyperparameter Tuning) 등 다양한 분야에서 반복 실험을 최소화하면서도 신뢰도 높은 조건을 탐색하는 데 활용되어 왔다[
14,
15].
이에 본 연구에서는 L-PBF 공정에서 지지 구조 없이 출력되는 오버행 구조(Support-free Overhang Structure)의 형상 정밀도 향상을 목표로, 초기 실험 데이터를 기반으로 공정 변수를 효율적으로 추천할 수 있는 베이지안 최적화 기법을 제안한다. 다양한 레이저 파워와 스캔 속도 조합으로 초기 실험을 수행하고, 획득된 출력물을 대상으로 기준 마스크와 실제 형상 간의 픽셀 단위 차이를 분석하는 이미지 기반 결함 채점(Scoring) 기법을 개발하였다. 이후 수집된 공정 변수와 품질 점수를 바탕으로 Gaussian Process Regression (GPR) 모델을 학습하고, 획득 함수(Acquisition Function)를 활용하여 베이지안 최적화를 수행하였다. 그러나, 단순 GPR 기반 대리 모델(Surrogate Model)은 외삽 영역에서 물리적으로 타당하지 않은 조건을 추천할 수 있다는 한계가 있으며, 최근에는 이를 보완하기 위한 물리 지식 기반(Physics-Informed) 접근이 제조 공정 분야에서 제안되고 있다[
16,
17]. 본 연구에서도 이러한 한계를 극복하고자 물리 제약이 반영된 Soft Penalty 항을 도입하여 대리 모델을 구성함으로써, 데이터가 존재하지 않는 영역에서도 물리적으로 일관된 조건을 추천할 수 있도록 하였다. 결과적으로, 본 연구는 반복 실험 없이도 L-PBF 기반 오버행 구조 제작에 적합한 공정 변수를 효과적으로 도출하였으며, 향후 복잡한 형상이나 다양한 공정 조건으로의 확장 가능성을 제시한다.
2. 실험 방법
2.1 장비 및 재료
본 연구에서는 Veltz사의 L-PBF 방식 3D 프린터(부산대학교 하이브리드 제조혁신엔지니어링 센터 구축 중)를 사용하였다. 본 장비의 베드 크기는 110 × 110 mm2이며, 레이저 스팟 직경은 50 μm이다. 사용한 금속 분말은 KOS사의 KOSMP-Ti-23(Ti-6Al-4V ELI, ASTM Grade 23) 티타늄 합금 분말이며, 입도 분포는 20-63 μm 범위이다.
2.2 오버행 구조 시편 설계 및 초기 실험 조건
본 연구에서 형상 품질 향상을 위한 최적화 대상은 지지 구조 없이 출력되는 경사각 5°의 오버행 구조이다. 공정 변수에 따른 오버행 구조의 형상 품질 저하와 결함 발생 특성을 분석하기 위해, 시편의 오버행 길이를 3, 6, 9 mm의 세 가지로 구분하고 각 길이별로 초기 실험을 수행하였다. 레이저 파워(P)는 40, 80, 120, 160, 200 W의 다섯 가지 수준으로 설정하였으며, 스캔 속도(V)는 400, 700, 1000, 1300, 1600 mm/s로 조절하였다. 이를 통해 다양한 공정 변수 조합에 따른 오버행 형상의 출력 실험을 수행하고, 형상 품질을 평가하여 대리 모델 구축을 위한 초기 실험 데이터를 구축하였다.
2.3 베이지안 최적화
베이지안 최적화는 목적 함수의 수학적 형태를 알 수 없고, 제한된 관측만 가능한 상황에서 최소한의 실험 횟수로 최적 조건을 탐색할 수 있도록 설계된 확률 기반 최적화 기법이다[
18]. 이때 목적 함수를 직접 평가하지 않고도 최적 조건을 추정하기 위해 대리 모델(Surrogate Model)을 구성하며, 이는 실제 실험을 대신하여 입력에 대한 결과를 예측한다. 대리 모델은 GPR 모델을 기반으로 하며, GPR은 각 입력 조건에 대해 함수의 예측 평균과 불확실도를 동시에 제공한다. 본 연구에서는 GPR 모델을 Python 기반의 GPyTorch 라이브러리를 이용해 구현하였으며, 커널 함수로는 Spectral Mixture (SM) 커널을 채택하였다. 커널(Kernel) 함수는 데이터 간의 유사도를 정의하며, GPR의 예측 형태를 결정하는 핵심 요소이다. 모델 학습은 Marginal Log Likelihood를 최대화하는 방식으로 수행되었으며, 각 GPR 모델은 최대 150회의 반복 학습을 통해 수렴되었다. 입력 변수로는 레이저 파워(P), 스캔 속도(V), 오버행 구조의 길이(L)이며, 출력 변수는 Underfill Score와 Overfill Score, 두 개의 품질 점수로 구성된다. 베이지안 최적화는 GPR 기반의 대리 모델과 획득 함수(Acquisition Function)를 활용하여 현재까지 관측된 최적값보다 더 나은 결과를 얻을 가능성이 높은 조건을 추천한다. 본 연구에서는 획득 함수로 Expected Improvement (EI)를 채택하였다. EI는 현재까지 관측된 최적 조건 대비 기대 개선량이 높은 지점을 우선적으로 탐색하도록 유도하며, 다음
식(1)과 같이 계산된다[
19].
여기서 μ(x)는 대리 모델 예측의 평균값, σ(x)는 예측의 표준편차, μmin은 현재까지의 대리 모델이 예측한 최소값, Φ(Z)와 ϕ(Z)는 각각 표준 정규분포의 누적분포함수와 확률밀도함수이다. ξ는 탐험(Exploration)과 활용(Exploitation) 간의 균형 조절을 위한 상수이며, 0.5로 설정하였다. 탐험은 불확실도가 높은 영역을 탐색하여 새로운 정보 획득을 우선시하는 전략이며, 활용은 이미 확보된 정보 중 유망한 조건 부근을 집중적으로 탐색하는 방식이다. 이 두 전략의 균형을 조절함으로써 최적 조건을 점진적으로 탐색한다. 최적화는 Scikit-optimize 라이브러리의 gp_minimize 함수를 활용해 수행되었다. 각 형상 길이별로 서로 다른 seed 값을 사용하여 베이지안 최적화를 50회 반복 수행하였으며, 그중 대리 모델의 예측값이 가장 낮은 조건을 최종 추천값으로 선택하였다. 본 연구는 베이지안 최적화를 통해 각 길이별로 물리 제약을 만족하면서 두 가지의 품질 점수를 동시에 최소화하는 공정 변수 조합(P, V)을 효과적으로 도출하였다.
3. 결과 및 고찰
3.1 L-PBF 공정에서의 오버행 형상 결함 유형 분석
오버행 형상을 적층 제조하는 과정에서
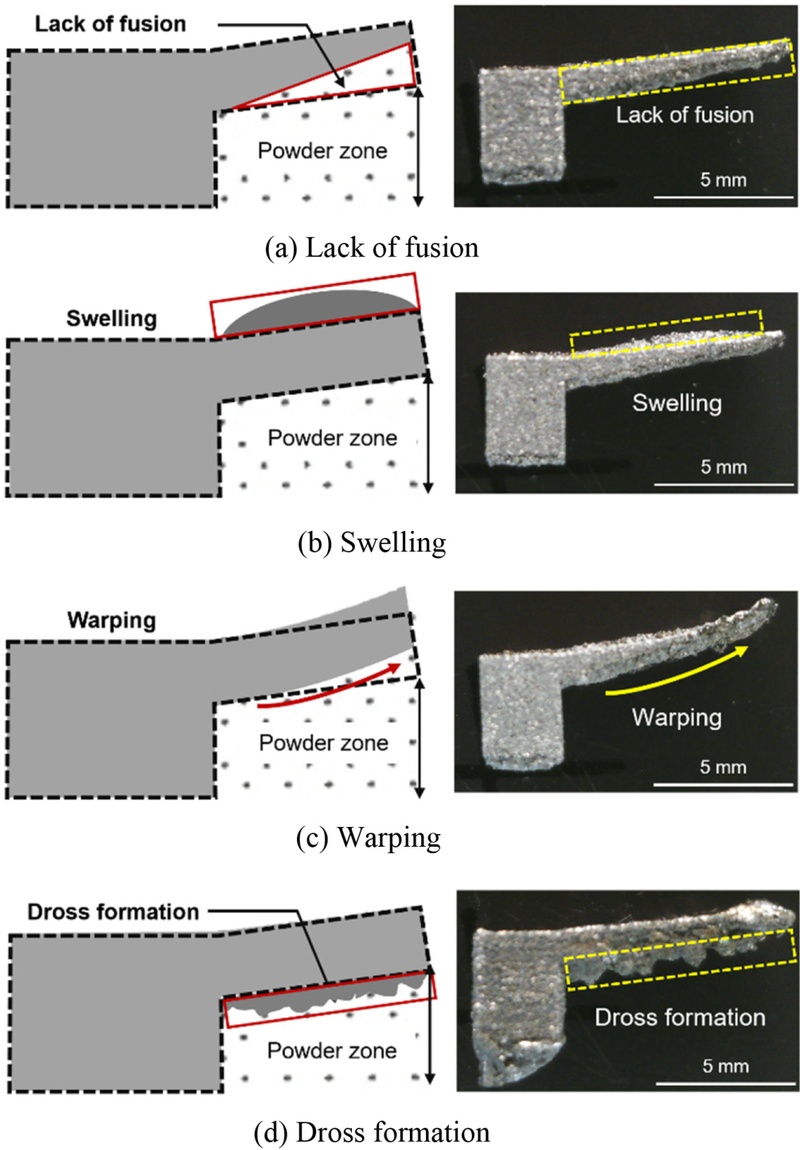
Fig. 1에 제시된 주요 결함들이 반복적으로 관찰되었다. 이러한 결함들은 공정 변수에 따른 에너지 밀도의 과부족, 냉각 속도의 불균형 등에 의해 발생한다.
Fig. 1(a)는 융합 부족(Lack of Fusion) 결함의 이미지로, 열 입력 부족 또는 재료의 불완전한 용융으로 인해 설계 형상보다 재료가 적게 적층되거나 일부 구조가 누락된 상태를 보여준다[
20]. 이는 주로 낮은 레이저 파워 또는 높은 스캔 속도에 의해 유효한 열 입력이 부족해지면서 발생한다. 해당 결함은 형상 정밀도를 저하시키고, 구조적 불완전성과 후속 적층 공정의 실패를 유발한다.
Fig. 1(b)는 팽윤(Swelling) 결함의 이미지로, 적층된 형상의 상부가 국부적으로 팽윤된 상태를 보여준다. 이러한 결함은 레이저 스캔 직후 Recoil Pressure가 Marangoni Convection보다 상대적으로 우세하게 작용하는 조건에서 발생한다[
21]. Recoil Pressure는 레이저 조사에 의해 금속이 기화하면서 발생하는 상향 압력으로, 용융풀 표면을 수직으로 압박하여 중심부의 용융 재료를 외곽으로 밀어낸다. 반면, Marangoni Convection은 표면의 온도 구배에 의해 발생하는 수평 방향의 표면장력 흐름으로, 용융풀 표면을 평탄화시키는 역할을 한다. 두 힘에 의해 형성된 유동이 충분히 마무리되기 전에 급속한 냉각이 발생하면, 용융 재료가 끝단에 잔류하며 응고되어 팽윤이 발생한다. 이 결함은 상위 레이어의 적층 안정성에도 부정적인 영향을 미칠 수 있다.
Fig. 1Defect types observed in overhang structures fabricated by L-PBF process
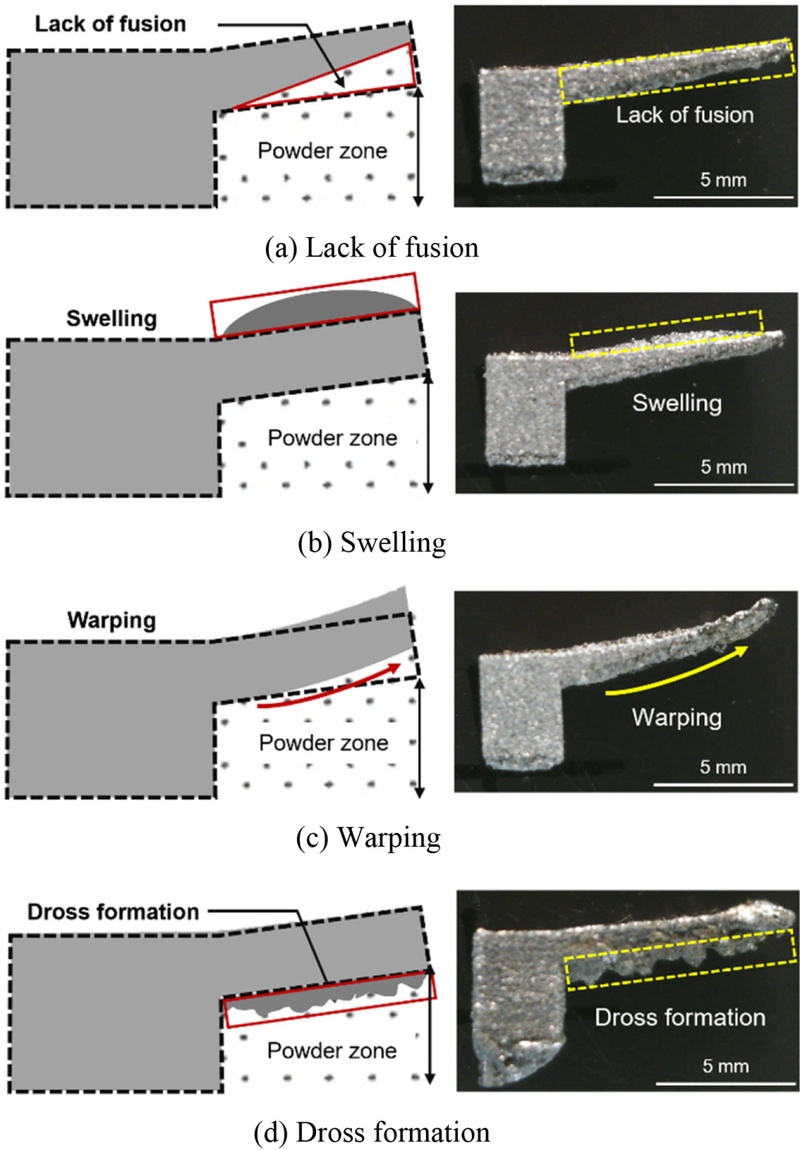
Fig. 1(c)는 뒤틀림(Warping) 결함의 이미지로, 출력물 상단이 위로 휘어져 설계 형상에서 벗어난 상태를 보여준다. 이 결함은 과도한 열 입력으로 인해 열에너지가 축적되고 냉각이 느리거나 비대칭적으로 진행될 때 발생한다. 오버행 구조의 하부는 고체 지지물이 아닌 파우더로 구성되어 있어, 열전달 경로가 단절되거나 점 접촉에 불과해 열이 효과적으로 분산되지 못하고 냉각도 불균일하게 이루어진다. 이러한 환경에서는 용융풀의 비대칭 수축과 열 잔류 응력의 축적으로 인해 Warping 결함이 발생한다[
22]. 이는 층간 간섭, 리코터와의 충돌, 출력물의 탈락 및 장비 손상 등으로 이어질 수 있다.
Fig. 1(d)는 잔류물(Dross) 형성 결함의 이미지로, 출력물 하단에 불규칙한 금속 응고물이 형성된 상태를 보여준다.
이 결함은 과도한 용융이 발생한 조건에서 하부에 지지 구조가 없을 경우 주로 발생하며, 중력과 표면장력의 복합 작용으로 인해 용융 금속이 파우더 사이로 침하하게 된다. 그 결과 기준 형상 하부에 덩어리 형태의 응고물이 형성된다[
23]. 이는 하부 형상의 불규칙성, 후처리 난이도 증가, 형상 오차를 유발한다. 이처럼 오버행 형상에서는 용융 및 응고 과정이 복합적으로 작용하며, 공정 중 열 입력량과 냉각 속도에 따라 다양한 결함이 유발될 수 있다. Lack of Fusion과 Swelling은 각각 열 에너지가 부족하거나 급속 냉각 조건에서 주로 발생하며, Warping이나 Dross 형성은 공정 중 과도한 열 축적으로 인해 유발된다. 본 연구에서는 이러한 결함을 완화하기 위해 레이저 파워와 스캔 속도를 주요 최적화 변수로 선정하였다.
본 연구에서는 오버행 구조의 형상 정밀도를 정량적으로 평가하기 위해 설계된 목표 형상으로부터 생성된 기준 마스크(Reference Mask)와 실제 적층 형상의 측면 이미지를 비교 분석하여 품질을 정량화하였다(
Fig. 2).
Fig. 2Defect scoring method based on image comparison between reference and printed shapes

우선, 실제 적층된 시편의 측면 이미지를 촬영한 뒤, 기준 마스크를 해당 이미지에 정렬하였다. 이후 이미지의 임계값(Threshold) 값을 조정하여 이진화(Binary Conversion)를 수행하였으며, 이 과정에서 발생할 수 있는 누락 영역은 Flood-fill 알고리즘을 활용한 후처리로 보정하였다. 본 연구는 오버행 형상 분석에 초점을 맞추어, 기준 형상의 하단 가장자리 두 점을 연결한 선(Baseline)을 기준으로 하여, 그 상단 영역만을 평가 대상으로 설정하였다. 이후 기준 형상과 실제 적층 형상 간의 동일 위치의 픽셀 값을 비교하여, 전체 영역을 세 가지 유형으로 분류하였다. 기준 마스크 내부에 해당하고, 이진화된 이미지의 픽셀 값이 255(흰색)인 경우는 기준 형상과 실제 적층 결과가 일치하는 영역으로, 정상 적층 영역(Correct)으로 정의하였다. 기준 마스크 내부에 속하지만, 픽셀 값이 0(검정색)인 경우는 적층이 이루어지지 않은 미적층 영역(Underfill)으로 분류된다. 마지막으로, 기준 마스크 외부에 해당하면서 픽셀 값이 255인 경우는, 기준 형상 외부에 재료가 적층된 과적층 영역(Overfill)으로 분류된다. 이러한 기준으로 영역을 분류하고, 두 가지 점수를 계산하였다. 각각은 아래의 식과 같이 정의된다.
이때, 두 점수의 분모는 기준 마스크 내부의 전체 면적(Correct + Underfill)으로 고정된다. 제안된 이미지 기반 품질 평가 방식은 형상 정밀도 저하와 연관된 Underfill과 Overfill을 중심으로 형상 품질을 정량적으로 평가하며, 각 공정 조건에 따른 결함 발생 경향을 비교 분석하는 데 유용하다. 특히, 기준 형상과의 정합도를 수치화함으로써 다양한 형상에도 활용 가능한 객관적이고 확장성 있는 품질 평가 방법을 제공한다.
3.3 베이지안 최적화 기반 공정 변수 추천
본 절에서는 오버행 구조의 적층 품질 향상을 목표로, 레이저 파워(P)와 스캔 속도(V)의 공정 변수 조합을 효율적으로 도출하기 위해 구성된 베이지안 최적화 프레임워크에 대해 상세히 기술한다.
3.3.1 품질 예측을 위한 GPR 모델 구조
먼저 다양한 오버행 구조의 길이(L= 3, 6, 9 mm)에 대해 실험을 수행하고, 각 길이에서의 공정 변수 조합(P, V)에 따른 두 가지 품질 점수를 3.2절에서 제시한 이미지 기반 채점 방식을 통해 수집하였다. 수집된 데이터를 기반으로 GPR 모델을 학습하였으며 입력 변수는 공정 조건(P, V, L), 출력 변수는 Underfill 및 Overfill 점수로 구성된다. GPR 학습 과정에서는 약 20회 이내에 손실 함수가 급격히 감소한 후, 각 품질 점수에 대해 1.33(Underfill Score), 1.38 (Overfill Score) 수준에서 안정적으로 수렴하였다. 이러한 수렴 양상은 학습 후반에 불필요한 진동 없이 일정한 loss 수준을 유지하고 있으며, 두 출력 변수 모두 유사한 수준에서 수렴하여 모델이 안정적으로 학습되었음을 시사한다.
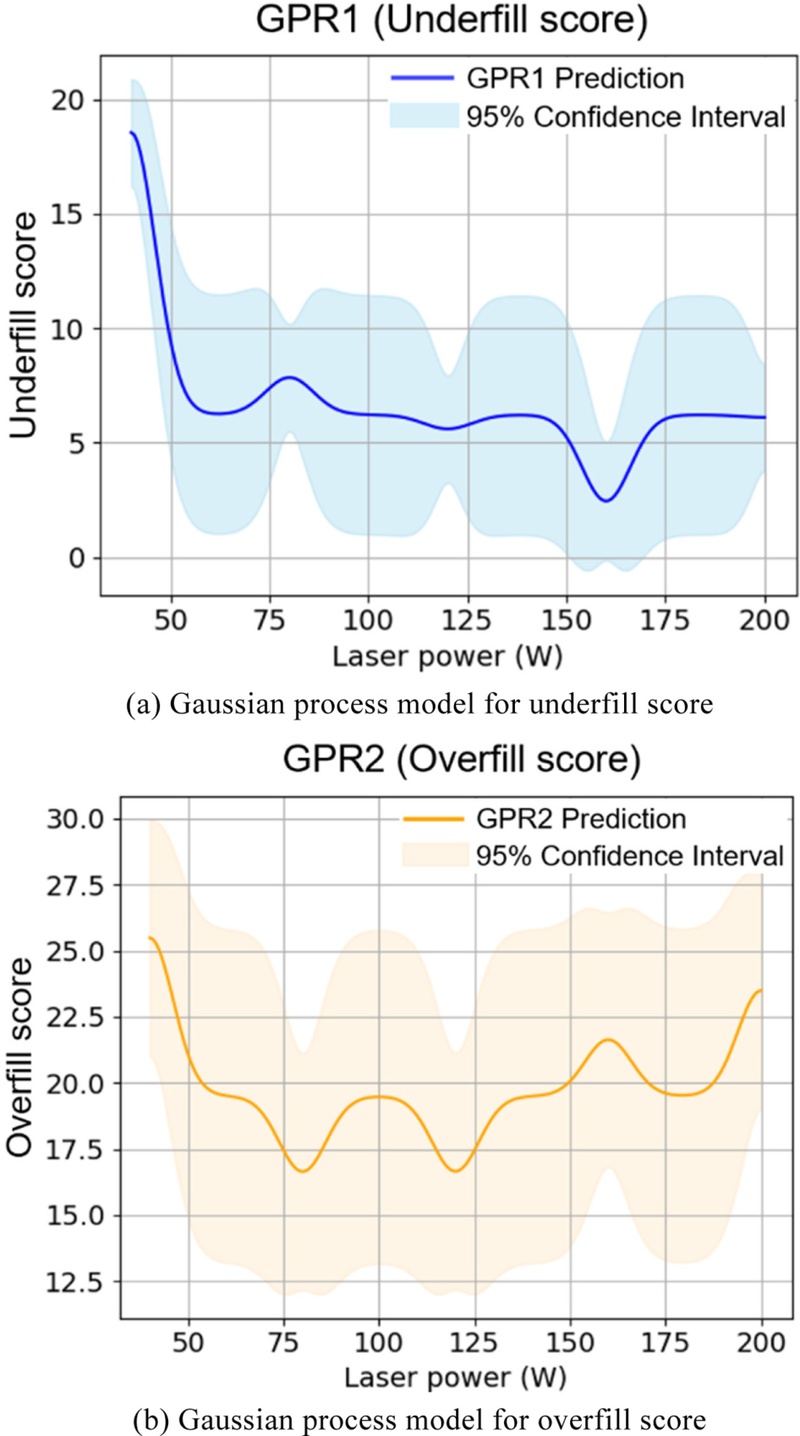
Figs. 3(a)와 3(b)는 각각의 품질 점수에 대해 독립적으로 학습된 GPR 모델의 예측 결과를 나타낸다. 이때
Figs. 3과
4는 직관적인 이해를 돕기 위해 L = 9 mm, V = 700 mm/s로 고정한 상태에서 P를 변화시킨 경우에 해당하며, 실제 모델은 세 입력 변수(P, V, L)를 모두 고려하는 고차원 함수로 구성된다.
Fig. 3GPR models for quality score prediction
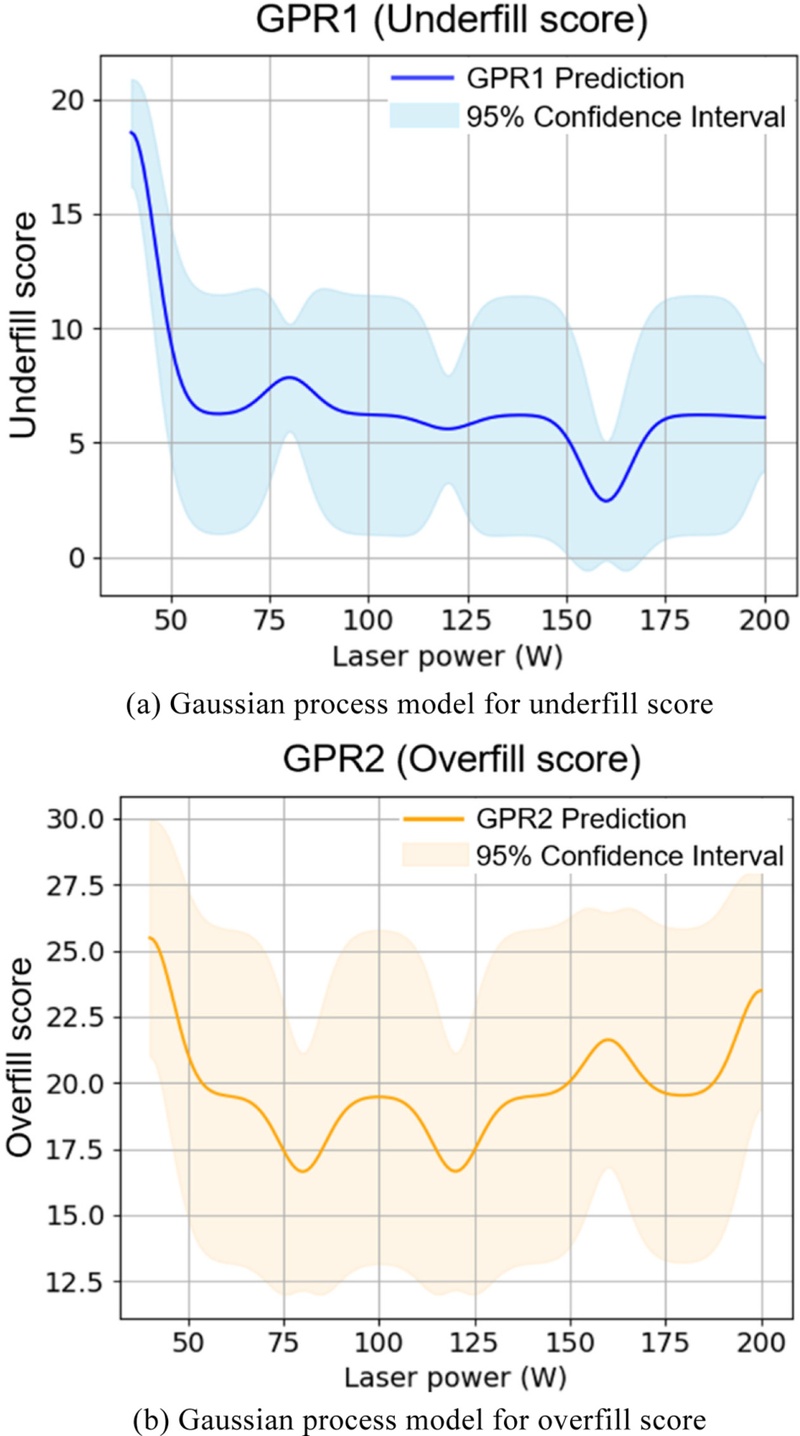
입력과 출력 간의 스케일 차이로 인해 발생할 수 있는 학습 불안정을 방지하기 위해, 모든 변수는 표준 정규화를 거쳤다. 커널 함수로는 Spectral Mixture (SM) 커널을 채택하였다. SM 커널은 다양한 주파수 성분을 조합하여 복잡한 비선형 함수를 효과적으로 모델링할 수 있으며, 특히 훈련 데이터의 입력 조건을 벗어나는 외삽(Extrapolation) 영역에서도 우수한 예측 성능을 보이는 것으로 알려져 있다[
24]. 본 연구에서는 SM 커널의 적합성을 평가하기 위해 RBF, Periodic, Rational Quadratic (RQ) 커널과의 비교 분석을 수행하였다.
각 커널에 대해 Underfill Score와 Overfill Score 예측 성능(Root Mean Square Error, RMSE)을 평가한 결과, SM 커널은 Underfill Score에서 가장 낮은 RMSE(1.29)를 기록하며 우수한 성능을 보였다. 타 커널들은 대체로 2.8 수준의 RMSE를 보였으며, SM 커널에 비해 다소 높게 나타났다. 반면, Overfill Score에서는 SM 커널이 5.91로 상대적으로 높은 RMSE를 보였으며, 다른 커널들은 1.3에서 3.0수준으로 비교적 안정적인 예측 성능을 보였다. 그러나 본 연구의 핵심은 예측 정확도 자체보다, 제한된 학습 데이터로부터 외삽 영역에서도 신뢰도 높은 조건을 효율적으로 추천하는 데에 있다.
이에 따라 커널의 신뢰도를 정량화할 수 있는 지표인 신뢰구간 폭(Confidence Interval Width)을 함께 고려하였다. 외삽 조건(L = 12 mm)에서 분석한 결과, SM 커널은 평균 신뢰구간 폭이 26.29로 가장 작고, 표준편차는 0.26으로 나타나, 입력 변화에 따른 예측 신뢰도가 안정적으로 유지됨을 확인할 수 있었다. RBF(평균 30.18, 표준편차 0.37), Periodic (34.72, 3.40), RQ(34.04, 0.26) 커널과 비교했을 때, SM 커널은 전반적으로 낮고 일관된 불확실성을 보였다. 이러한 특성은 모델이 특정 영역에 대해 얼마나 높은 확신을 가지고 있는지를 반영하며, 특히 Bayesian Optimization (BO) 수행 시에도 중요한 요소로 작용한다. 예측 불확실성이 지나치게 요동치는 경우 BO의 조건 추천이 왜곡될 수 있는 반면, SM 커널은 비교적 안정적인 신뢰도를 바탕으로 외삽 영역에서도 일관된 조건 추천이 가능하다는 점에서, 본 연구의 최적화 목적에 부합하는 커널로 판단된다.
3.3.2 물리 기반 제약을 반영한 대리 모델 설계
본 연구에서는 두 개의 GPR 모델의 예측 평균을 합산하여 대리 모델의 기본 구조를 구성하였다. 그러나 실험 데이터가 확보되지 않은 다양한 오버행 길이에 대해서도 신뢰성 있는 공정 변수 추천이 가능하도록, 공정 특성에 기반한 물리적 경향성을 모델에 반영할 필요가 있었다. 오버행 구조의 특성상 길이가 길어질수록 출력 중 열이 축적되면서 Warping이나 Dross와 같은 결함이 발생할 가능성이 높아진다. 따라서 형상 정밀도를 확보하기 위해서는 오버행 길이에 비례하여 공급되는 에너지 밀도(ρ)를 점진적으로 감소시키는 방향의 제약이 필요하다. 이러한 경향을 모델에 반영하기 위해, 본 연구에서는 Soft Penalty 항을 도입하였다. 이 항은 에너지 밀도가 오버행 길이에 따라 회귀 기반으로 추정된 에너지 밀도(ρ*)에서 벗어나는 정도에 따라 벌점을 부여하며, 대리 모델에 통합된다. ρ*는 초기 실험에서 확보된 오버행 길이 6 및 9 mm 조건의 최적 에너지 밀도를 비교한 후, 두 조건 간의 차이를 선형 회귀 방식으로 환산하여 설정하였다. 이를 통해 길이에 따라 점진적으로 감소하는 형태의 ρ* 식이 정의되었다.
Penalty 항은 완충 구간을 포함하는 Huber-type Soft Penalty 함수로 구성되며, 수식은 다음
식(4)와 같다.
여기서
ω는 Penalty Weight,
δ는 허용 오차 범위이며, 본 연구에서는
ω = 1000,
δ = 0.1로 설정하였다. Huber-Type Penalty는 회귀 기반 추정 에너지 밀도에서 크게 벗어나는 조건에 대해 최적화 탐색을 제한함으로써, 물리적으로 타당하지 않은 조건의 선택을 억제하는 역할을 수행한다. 이와 같이 구성된 Penalty 항은 대리 모델에 통합되어, 데이터가 없는 오버행 조건에 대해서도 형상 정밀도를 확보할 수 있는 공정 변수를 추천한다.
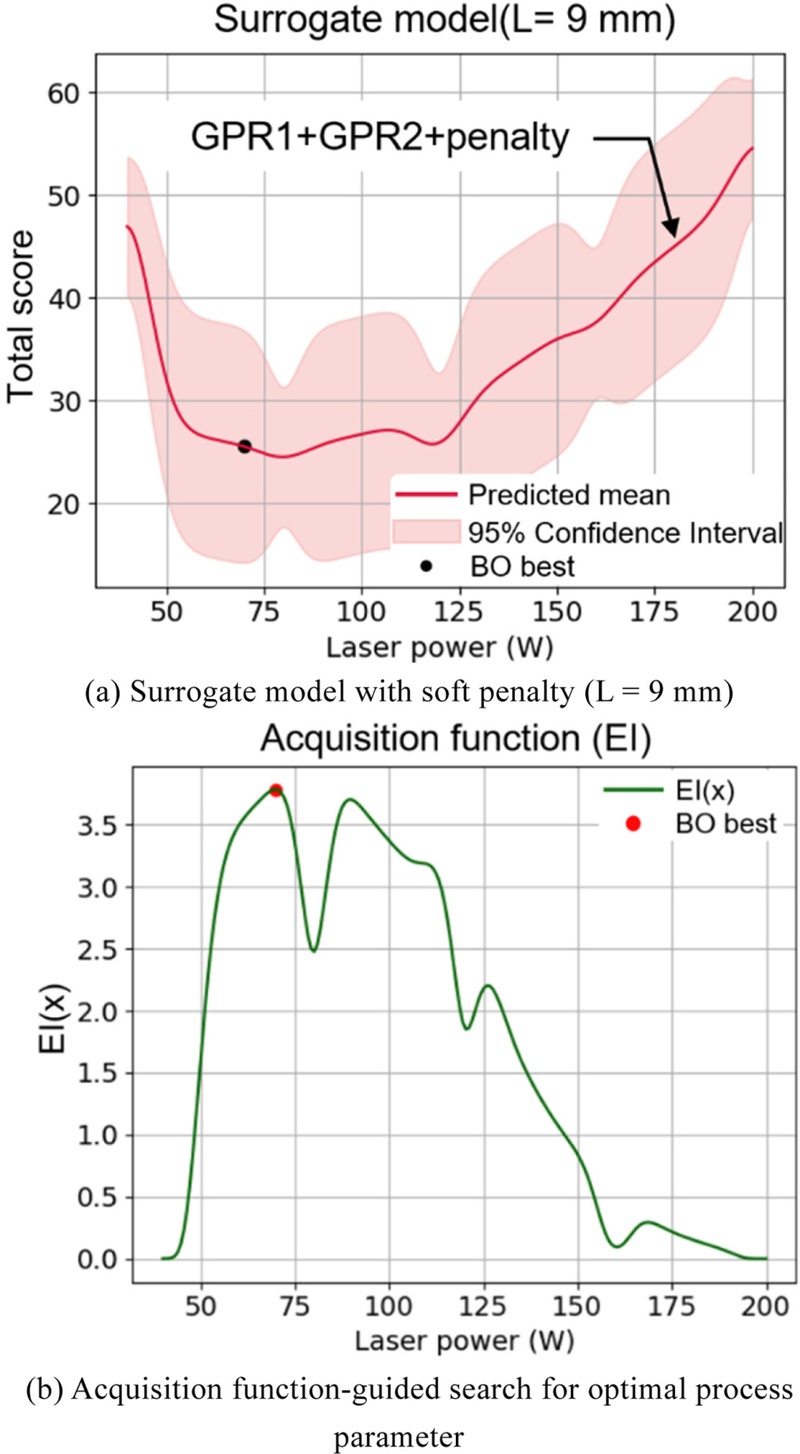
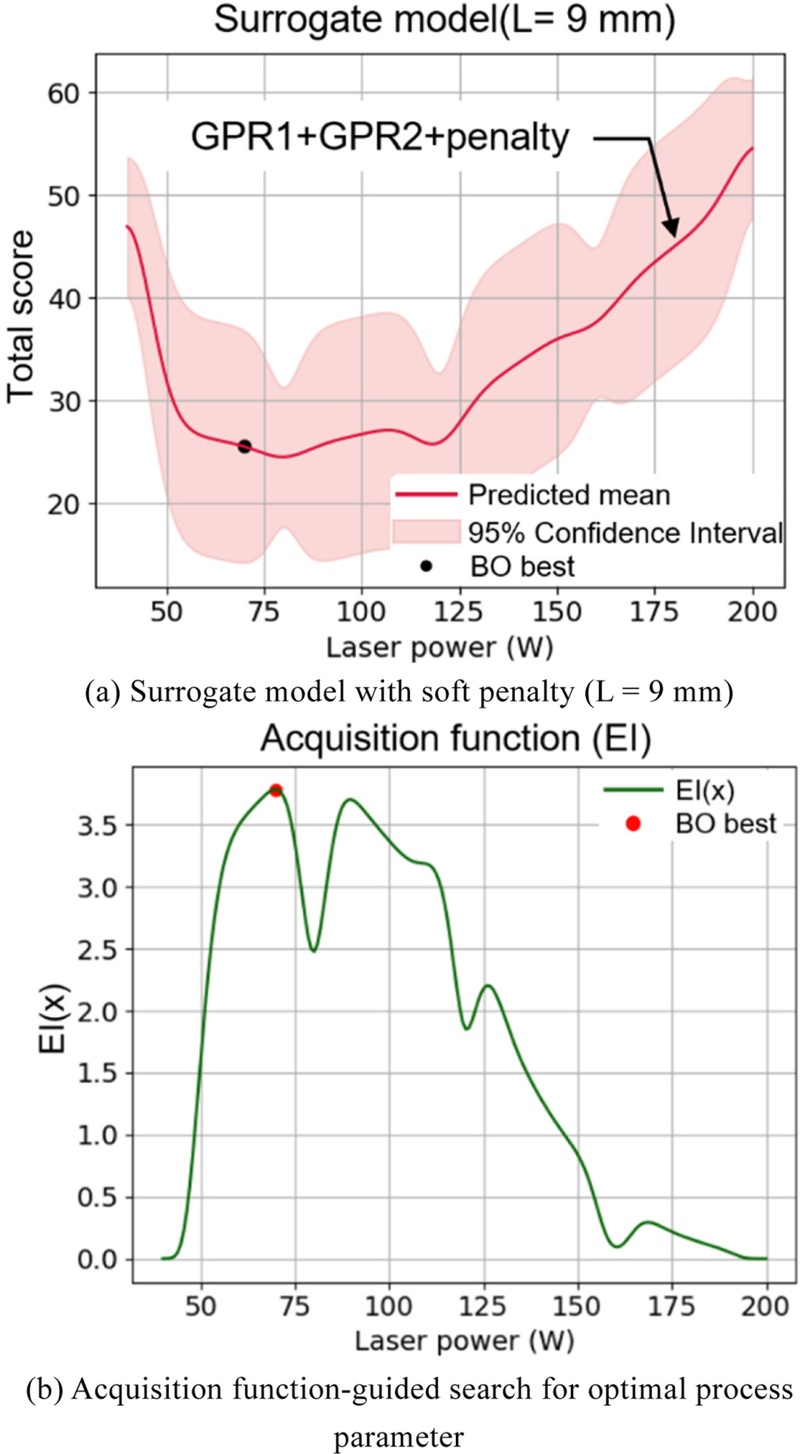
Fig. 4(a)는 Penalty 항이 적용된 대리 모델이 전체 실험 경향을 따르면서도, 출력 가능성이 높은 조건 범위 내에서 예측 점수가 낮게 형성됨을 시각적으로 보여준다. 한편, 본 연구에서는
ρ*를 오버행 길이에 따라 선형적으로 감소하는 형태로 설정하였으나, 향후 긴 오버행 구조에서의 적용을 고려할 경우, 하한값을 부여하거나 비선형 완화 함수를 도입하는 방향도 추후 연구로 고려될 수 있다.
Fig. 4Surrogate model and optimization result for 9 mm overhang length
3.3.3 대리 모델 및 획득 함수를 활용한 베이지안 최적화 절차
본 연구에서는 각 오버행 길이 조건에 대해 BO를 50회 반복 수행하였으며, 매 반복마다 Expected Improvement (EI) 함수에 기반하여 가장 기대 개선량을 가지는 공정 변수를 선택하였다.
EI 함수는 대리 모델의 예측 평균과 불확실도를 동시에 고려하여 기대 개선량이 큰 조건을 우선적으로 탐색하도록 유도한다. 최적화는 오버행 길이 L을 고정한 상태에서 수행되었으며, 각 L에 대해 최적의 공정 변수 조합(P, V)을 도출하는 방식으로 구현되었다. 특히 본 연구의 목적은 기존 실험 데이터의 범위를 넘어서는 오버행 조건에서도, 물리적으로 타당한 공정 변수를 추천하는 것이며, 이를 위해 Soft Penalty 항이 포함된 대리 모델을 활용하였다. 총 50회의 반복 동안, 초기 약 5회 내에 대리 모델 값이 급격히 감소한 뒤, 반복 25회 이후에는 대리 모델 예측값의 최소값이 일정하게 유지되며 수렴하였다.
Fig. 4(b)는 EI 함수 기반의 탐색 결과를 시각적으로 나타낸 것이며, 기대 개선량이 가장 높은 지점이 최적 변수로 선택되는 과정을 보여준다. 추천된 변수의 대리 모델 예측값은
Fig. 4(a)를 통해 확인할 수 있다.
본 절에서는 오버행 길이 12, 15, 18 mm에 대해 베이지안 최적화를 적용하여 공정 변수(P, V)를 도출하고, 그 결과를 분석한다. 해당 조건들은 모두 외삽 영역에 해당하며, GPR 기반 대리 모델은 기존 데이터의 경향을 바탕으로 예측을 수행하였다. 에너지 밀도 기반 Soft Penalty항은 과도하게 높은 또는 낮은 에너지 밀도가 추천되는 것을 억제하였다.
3.4.1 기존 실험 데이터 경향과 비교한 대리 모델의 예측 결과
베이지안 최적화 결과의 타당성을 평가하기 위해, 대리 모델이 기존 실험 데이터의 경향을 얼마나 잘 반영하고 있는지를 검토하였다.
본 절에서는 길이 9 mm 조건에서의 실험 결과와 길이 12 mm 조건에 대한 대리 모델의 예측 결과를 비교 분석하였다.
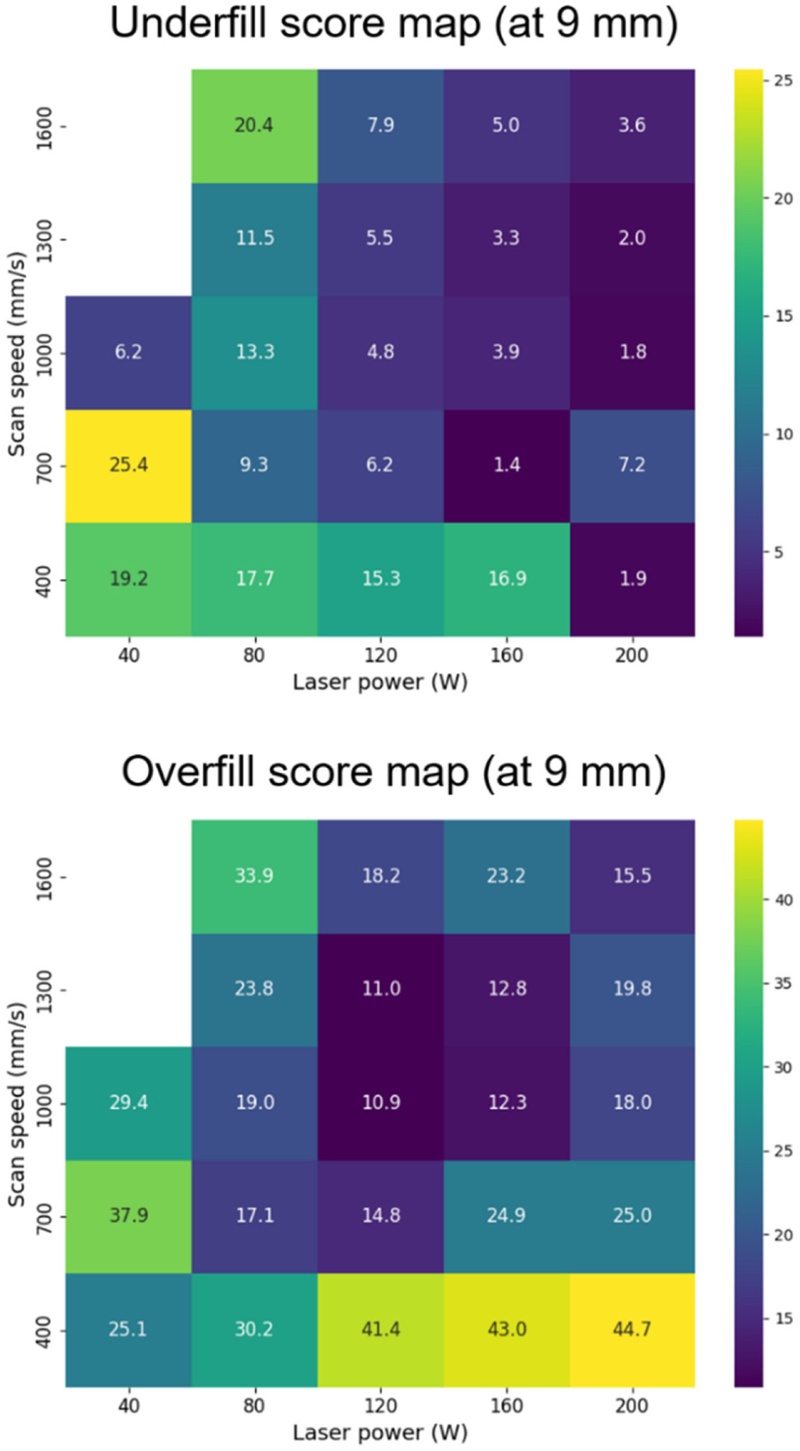
Fig. 5는 9 mm 조건에서 다양한 P-V 조합에 대해 실제 실험을 통해 측정된 Underfill과 Overfill 점수의 분포를 나타낸다. Underfill 점수는 목표 형상 내부의 미적층 영역 비율을 정량화한 지표로, 내부 충진이 충분할수록 점수가 낮아진다. 일반적으로 공급된 에너지가 부족할 경우 Underfill 점수가 높게 나타나며, P가 커지거나 V가 작아질수록 점수는 감소하는 경향을 보인다. 한편 일부 저속 조건(400-700 mm/s)에서는 에너지 밀도가 충분함에도 불구하고 Underfill 점수가 오히려 높게 측정되었다. 이는 실제 출력된 시편에서 형상 상단이 위로 휘어지는 Warping 현상이 관찰되었기 때문이다. Warping이 발생하면 적층 표면이 들리면서, 측면 기준에서 하단이 비어 보이는 영역이 생겨 Underfill 점수가 높아진다. Overfill 점수는 기준 형상을 초과하여 재료가 증착된 정도를 나타내며, P가 커지거나 V가 작아질수록 점수는 증가하는 경향을 보인다. 실제 실험에서도 에너지 밀도가 높은 조건에서는 과도한 용융 및 열 축적으로 인한 Warping 또는 Dross 현상이 발생하여 기준 형상을 초과한 적층이 확인되었고, 이에 따라 Overfill 점수가 상승하였다. 반면, 일부 낮은 에너지 밀도 조건에서도 예외적으로 높은 Overfill 점수가 측정되었는데, 이는 출력물의 윗면에서 국소적인 Swelling 현상이 발생한데에 기인한다.
Fig. 5Underfill and overfill score maps for 9 mm overhang structure across various P-V combinations
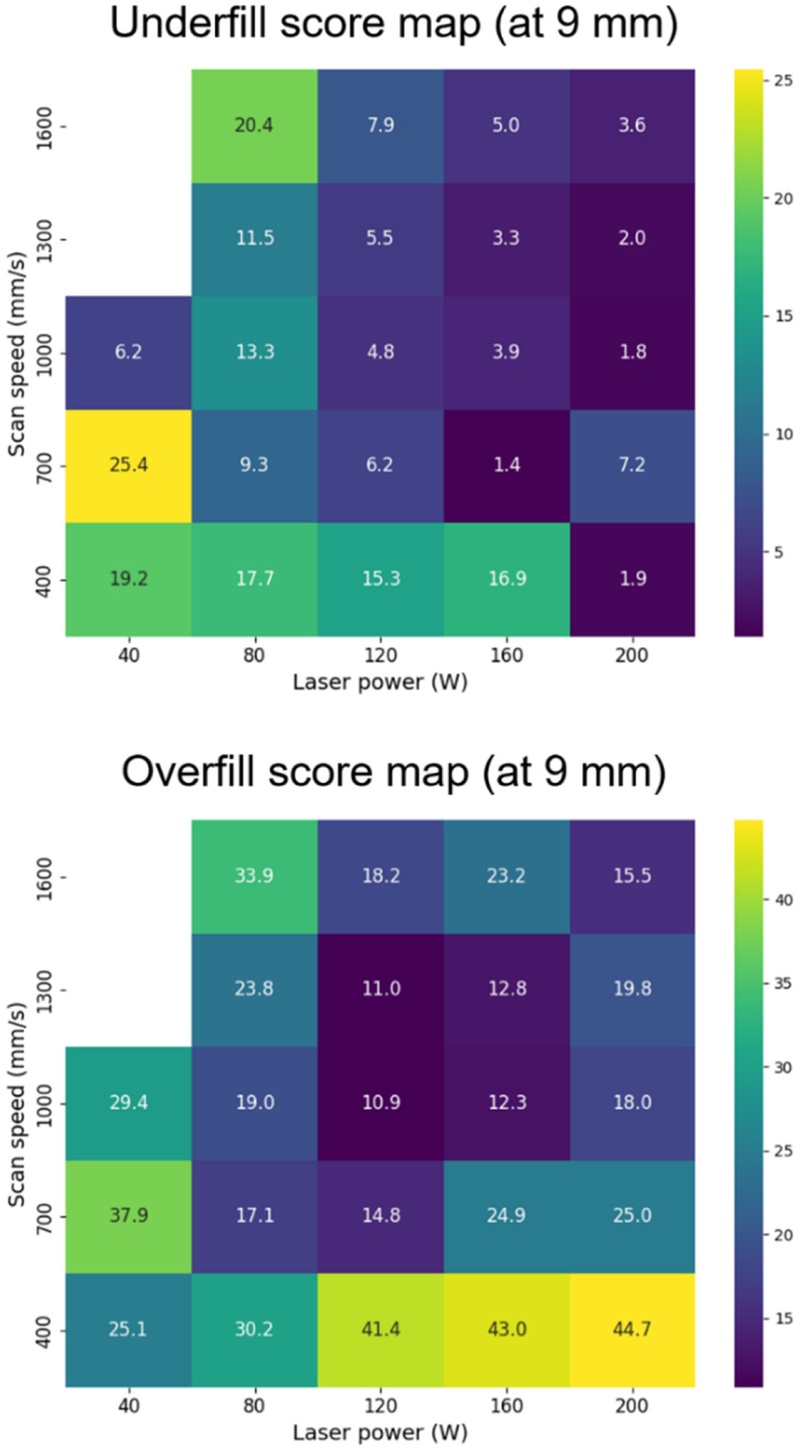
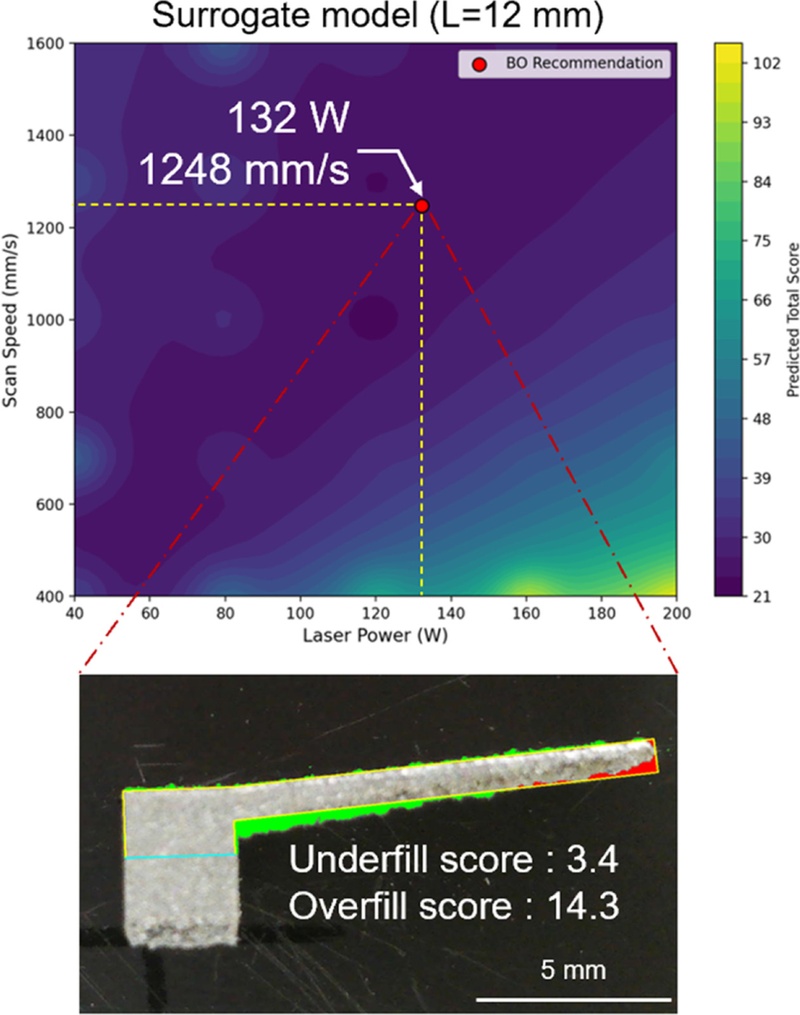
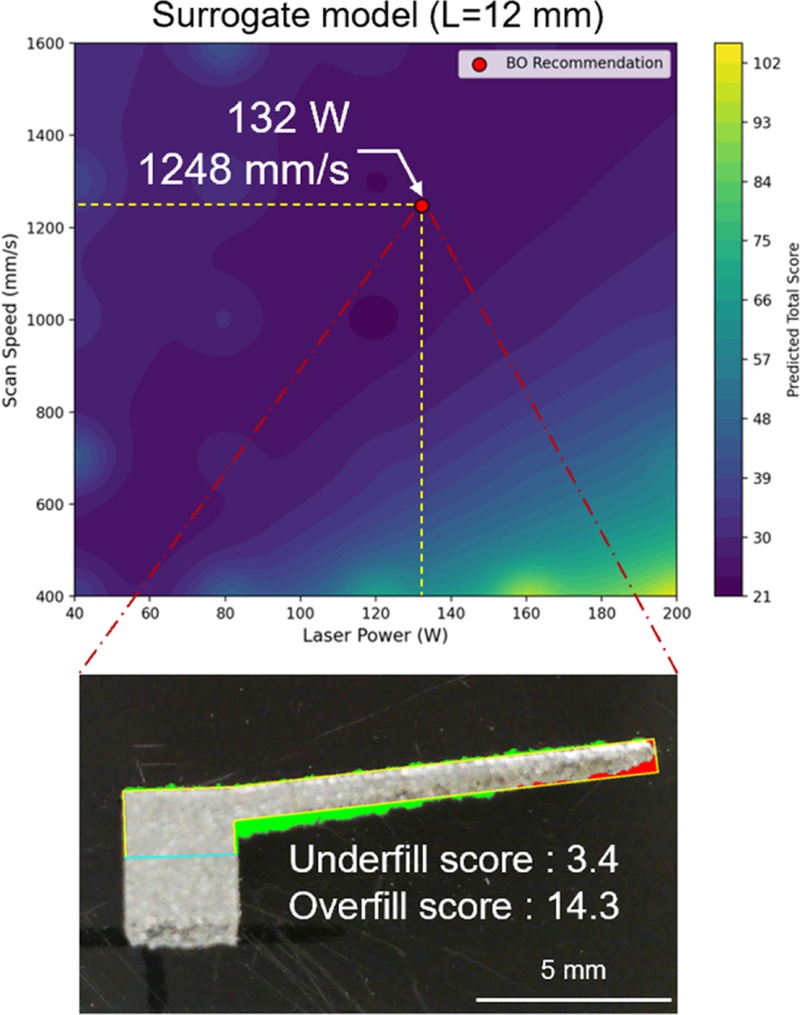
Fig. 6은 오버행 길이 12 mm 조건에서 대리 모델이 예측한 평균 점수 분포와 베이지안 최적화를 통해 도출된 추천 공정 변수, 그리고 해당 조건으로 출력한 시편 결과를 함께 보여준다. 대리 모델 예측 결과는 앞서 9 mm 조건에서 관측된 실험 경향과 유사하게, 고에너지 밀도 영역에서는 Warping이나 Dross 발생 가능성에 따라 높은 점수가 예측되었으며, 반대로 지나치게 낮은 에너지 밀도(주로 높은 V)에서는 상부의 Swelling 현상으로 인한 점수 상승이 관찰되었다. 또한, Penalty 항의 적용으로 인해 예측 점수는 회귀 기반 추정 에너지 밀도(
ρ*) 0.102 (L = 12 mm 기준) 근방에서 낮게 형성되었다. 실제 베이지안 최적화를 통해 도출된 최적 공정 변수는 132 W, 1248 mm/s로, 계산된 에너지 밀도는 약 0.105로
ρ*와 매우 근접하였다. 이는 Penalty 항을 통한 물리 기반 제약이 최적화 경로에 효과적으로 반영되었음을 시사한다. 추천된 공정 변수로 출력한 결과, Underfill 점수는 3.4, Overfill 점수는 14.3으로 형상 정밀도 측면에서 양호한 출력 품질을 확보할 수 있었다. 다만, 시편의 초기 구간에는 고출력 조건에 따른 소규모 Dross 형성이 관찰되었으나, 이는 공정 특성상 불가피한 형상이며, 전체적으로는 안정적인 형상 정밀도를 구현한 것으로 평가된다.
Fig. 6Surrogate model, recommended process parameters, and printed result for 12 mm overhang structure
3.4.2 외삽 영역 오버행 조건에 대한 최적 공정 변수 추천 결과
앞선 절에서는 오버행 길이 12 mm 조건에 대한 대리 모델의 예측 타당성을 검토하였다. 이를 바탕으로, 15와 18 mm 조건에 대해 베이지안 최적화를 수행하였다. 해당 조건들은 오버행 길이의 증가로 인해 열 축적이 심화되고 형상 정밀도 확보가 어려워지는 고난이도 형상에 해당한다. 각 오버행 길이에 대해 추천된 공정 변수와 실제 출력 결과는
Figs. 7과
8에 제시하였다. 이때, 최적화 성능 비교를 위해, 공정 변수 탐색 범위의 중간값인 120 W, 1000 mm/s를 기준 공정 변수로 설정하였다.
Fig. 7Comparison of process parameters for the 15 mm overhang structure

Fig. 8Comparison of process parameters for the 18 mm overhang structure
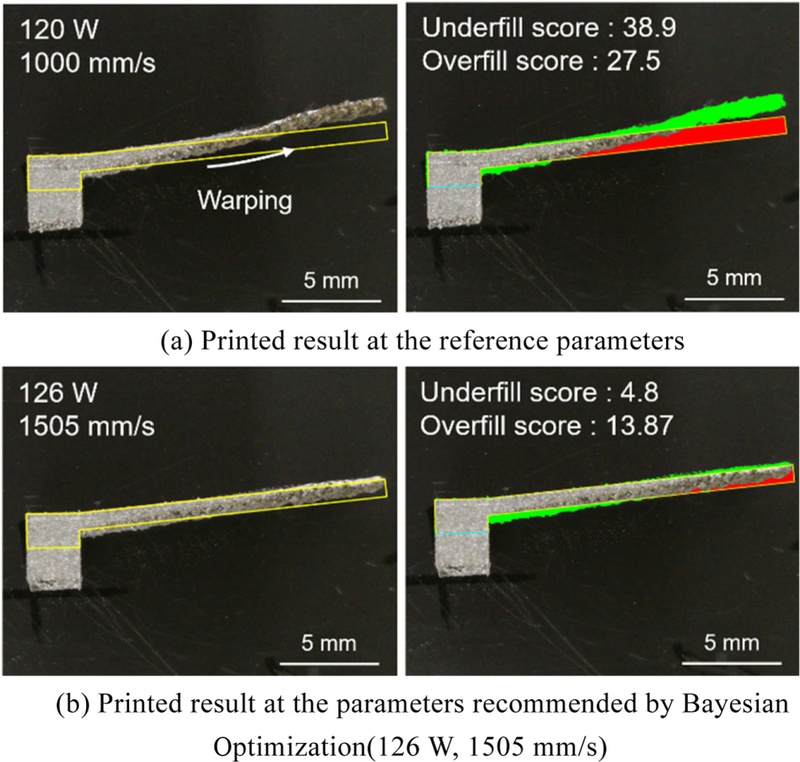
Fig. 7(a)는 15 mm 조건에서 기준 공정 변수로 출력한 결과이며, Warping 현상이 관찰되었다. 반면
Fig. 7(b)는 베이지안 최적화로 도출된 공정 변수(102 W, 1095 mm/s)로 출력한 결과이며, Warping이 억제되었고 Underfill 점수는 2.6, Overfill 점수는 16.5로 형상 정밀도의 개선이 확인되었다. 특히, Underfill 점수의 급감은 적층 안정성이 확보되었음을 의미한다.
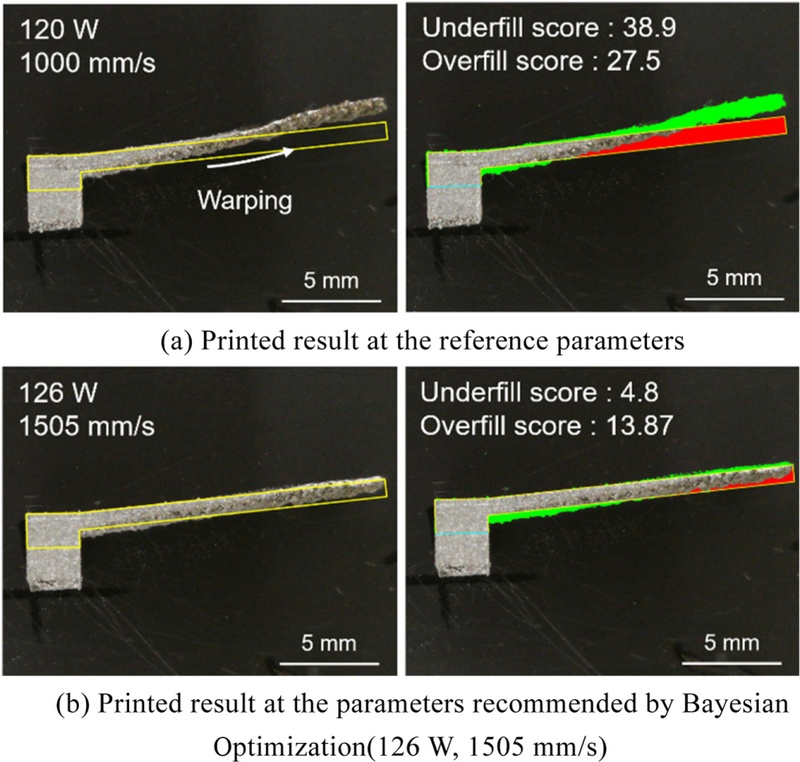
Fig. 8(a)는 18 mm 조건에서 기준 공정 변수로 출력한 결과로, 심각한 Warping이 발생한 것을 보여준다.
Fig. 8(b)는 베이지안 최적화를 통해 도출된 공정 변수(126 W, 1505 mm/s)로 출력한 결과이며, Underfill 점수는 4.8, Overfill 점수는 13.87로 기준 공정 변수 결과에 비해 품질이 전반적으로 개선된 양상을 보였다. 추천된 변수는 오버행 길이가 증가함에 따라 에너지 밀도가 점진적으로 감소하는 방향으로 조정되었다.
L = 12 mm 조건에서는 약 0.105, L = 15 mm와 18 mm 조건에서는 각각 약 0.093, 0.084 수준으로 낮아졌다. 이는 오버행 길이가 길어질수록 열 축적이 심화되며 Warping 결함이 두드러지고, 이로 인해 Underfill 및 Overfill 점수가 함께 상승하는 경향이 나타났기 때문이다. 이러한 결함에 대응하기 위해, 최적화는 적정 에너지 밀도 범위 내에서 결함을 완화할 수 있는 방향으로 공정 변수를 도출하였다.
이러한 결과는 베이지안 최적화가 단순히 점수의 최솟값만을 추구하는 것이 아니라, 결함 없이 출력 가능한 에너지 밀도 범위 내에서 최적의 공정 변수를 탐색했음을 의미한다. 이는 본 연구에서 구축한 GPR 기반 대리 모델이 실험 기반 경향성과 물리 기반 제약을 효과적으로 통합하고 있음을 보여준다. 특히, 외삽 영역에서도 우수한 형상 정밀도를 확보할 수 있는 공정 변수를 효율적으로 추천하였으며, 실제 적층 실험을 통해 그 재현성과 실효성이 입증되었다.
4. 결론
본 연구에서는 단순 기초 실험 (3, 6, 9 mm 오버행 구조)을 기반으로, GPR 모델과 물리 기반 Penalty 항을 결합한 대리 모델을 구축하였으며, 이를 활용하여 외삽 영역(12, 15, 18 mm)에 대한 공정 변수를 베이지안 최적화 방식으로 추천하였다. 제안된 최적화 기법은 사전 실험이 제한적인 상황에서도 고난이도 오버행 형상에 대해 물리적으로 타당하며 형상 결함이 억제된 공정 변수를 효율적으로 도출할 수 있음을 입증하였다. 오버행 구조의 초기 구간에서 나타나는 Dross 형상으로 인한 형상 정밀도 저하는 완전히 제거되지는 않았으나, 제안된 최적 공정 변수로 그 영향을 유의미하게 감소시킬 수 있었다.
또한, 본 연구에서 제안한 최적화 프레임워크는 초기 실험 데이터를 기반으로 GPR 모델을 학습하고, 여기에 물리적 제약 조건을 반영하여 베이지안 최적화를 수행하는 구조로 설계되었다. 이 구조는 품질 평가 기준이나 제약 조건이 대상 재료나 공정에 따라 달라질 수는 있으나, 전체적인 최적화 흐름은 동일하게 유지될 수 있어 다양한 형상 및 재료 조건에 적용 가능한 최적화 방식으로 확장 가능함을 보여주었다. 아울러, 향후 연구에서는 실험만으로는 사전에 파악하기 어려운 열 축적 경향이나 물리적 한계를 보완하기 위해, 시뮬레이션 기반 열 해석을 병행함으로써 보다 정량적이고 신뢰성 있는 제약 조건을 도출할 수 있을 것으로 기대된다.
ACKNOWLEDGMENTS
이 과제는 부산대학교 기본연구지원사업(2년)에 의하여 연구되었음.
REFERENCES
- 1.
Riva, L., Ginestra, P. S., Ceretti, E., (2021), Mechanical characterization and properties of laser-based powder bed-fused lattice structures: A review, The International Journal of Advanced Manufacturing Technology, 113, 649-671.
10.1007/s00170-021-06631-4
- 2.
Narasimharaju, S. R., Zeng, W., See, T. L., Zhu, Z., Scott, P., Jiang, X., Lou, S., (2022), A comprehensive review on laser powder bed fusion of steels: Processing, microstructure, defects and control methods, mechanical properties, current challenges and future trends, Journal of Manufacturing Processes, 75, 375-414.
10.1016/j.jmapro.2021.12.033
- 3.
Catchpole-Smith, S., Sélo, R., Davis, A., Ashcroft, I., Tuck, C., Clare, A., (2019), Thermal conductivity of tpms lattice structures manufactured via laser powder bed fusion, Additive Manufacturing, 30, 100846.
10.1016/j.addma.2019.100846
- 4.
Yang, L., Han, C., Wu, H., Hao, L., Wei, Q., Yan, C., Shi, Y., (2020), Insights into unit cell size effect on mechanical responses and energy absorption capability of titanium graded porous structures manufactured by laser powder bed fusion, Journal of the Mechanical Behavior of Biomedical Materials, 109, 103843.
10.1016/j.jmbbm.2020.103843
- 5.
Hussain, A., Kim, D., (2025), Fabrication of metal alloy structures with overhang features in laser-based powder bed fusion: A critical review of challenges and latest developments, Journal of Manufacturing Processes, 135, 112-130.
10.1016/j.jmapro.2025.01.031
- 6.
Khairallah, S. A., Anderson, A. T., Rubenchik, A., King, W. E., (2016), Laser powder-bed fusion additive manufacturing: Physics of complex melt flow and formation mechanisms of pores, spatter, and denudation zones, Acta Materialia, 108, 36-45.
10.1016/j.actamat.2016.02.014
- 7.
Yang, G., Li, H., Li, Z., Zhu, Z., Liu, R., Zhang, Q., Liu, Y., Yao, J., (2023), Support design of overhanging structure for laser powder bed fusion, Journal of Materials Research and Technology, 24, 8693-8702.
10.1016/j.jmrt.2023.05.087
- 8.
Yang, T., Liu, T., Liao, W., Wei, H., Zhang, C., Chen, X., Zhang, K., (2021), Effect of processing parameters on overhanging surface roughness during laser powder bed fusion of alsi10mg, Journal of Manufacturing Processes, 61, 440-453.
10.1016/j.jmapro.2020.11.030
- 9.
Han, Q., Gu, H., Soe, S., Setchi, R., Lacan, F., Hill, J., (2018), Manufacturability of alsi10mg overhang structures fabricated by laser powder bed fusion, Materials & Design, 160, 1080-1095.
10.1016/j.matdes.2018.10.043
- 10.
Lee, K.-H., Yun, G. J., (2022), Design optimization of thermally conductive support structure for laser powder-bed fusion process with part-scale thermal history, Additive Manufacturing, 51, 102627.
10.1016/j.addma.2022.102627
- 11.
Oster, S., Breese, P. P., Ulbricht, A., Mohr, G., Altenburg, S. J., (2024), A deep learning framework for defect prediction based on thermographic in-situ monitoring in laser powder bed fusion, Journal of Intelligent Manufacturing, 35(4), 1687-1706.
10.1007/s10845-023-02117-0
- 12.
Ogoke, F., Lee, W., Kao, N.-Y., Myers, A., Beuth, J., Malen, J., Barati Farimani, A., (2023), Convolutional neural networks for melt depth prediction and visualization in laser powder bed fusion, The International Journal of Advanced Manufacturing Technology, 129(7), 3047-3062.
10.1007/s00170-023-12384-z
- 13.
Frazier, P. I., (2018), A tutorial on bayesian optimization, arXiv preprint arXiv:
1807.02811.
- 14.
Wang, K., Dowling, A. W., (2022), Bayesian optimization for chemical products and functional materials, Current Opinion in Chemical Engineering, 36, 100728.
10.1016/j.coche.2021.100728
- 15.
Wu, J., Chen, X.-Y., Zhang, H., Xiong, L.-D., Lei, H., Deng, S.-H., (2019), Hyperparameter optimization for machine learning models based on bayesian optimization, Journal of Electronic Science and Technology, 17(1), 26-40.
- 16.
Kobayashi, W., Otsuka, T., Wakabayashi, Y. K., Tei, G., (2025), Physics-informed bayesian optimization suitable for extrapolation of materials growth, npj Computational Materials, 11(1), 36.
10.1038/s41524-025-01522-8
- 17.
Qiang, B., Shi, K., Liu, N., Ren, J., Shi, Y., (2023), Integrating physics-informed recurrent gaussian process regression into instance transfer for predicting tool wear in milling process, Journal of Manufacturing Systems, 68, 42-55.
10.1016/j.jmsy.2023.02.019
- 18.
Greenhill, S., Rana, S., Gupta, S., Vellanki, P., Venkatesh, S., (2020), Bayesian optimization for adaptive experimental design: A review, IEEE Access, 8, 13937-13948.
10.1109/ACCESS.2020.2966228
- 19.
Gan, W., Ji, Z., Liang, Y., (2021), Acquisition functions in bayesian optimization, Proceeings of the 2021 2nd International Conference on Big Data & Artificial Intelligence & Software Engineering (ICBASE), 129-135.
10.1109/ICBASE53849.2021.00032
- 20.
Mukherjee, T., DebRoy, T., (2018), Mitigation of lack of fusion defects in powder bed fusion additive manufacturing, Journal of Manufacturing Processes, 36, 442-449.
10.1016/j.jmapro.2018.10.028
- 21.
Tang, C., Le, K. Q., Wong, C. H., (2020), Physics of humping formation in laser powder bed fusion, International Journal of Heat and Mass Transfer, 149, 119172.
10.1016/j.ijheatmasstransfer.2019.119172
- 22.
Vastola, G., Sin, W., Sun, C.-N., Sridhar, N., (2022), Design guidelines for suppressing distortion and buckling in metallic thin-wall structures built by powder-bed fusion additive manufacturing, Materials & Design, 215, 110489.
10.1016/j.matdes.2022.110489
- 23.
Feng, S., Kamat, A. M., Sabooni, S., Pei, Y., (2021), Experimental and numerical investigation of the origin of surface roughness in laser powder bed fused overhang regions, Virtual and Physical Prototyping, 16(sup1), S66-S84.
10.1080/17452759.2021.1896970
- 24.
Ulrich, K. R., Carlson, D. E., Dzirasa, K., Carin, L., (2015), Gp kernels for cross-spectrum analysis, Advances in Neural Information Processing Systems, 28.
Biography
- Kyung Lim Oh
M.S. student in the Department of Mechanical Engineering, Pusan National University. Her research interests are metal-based additive manufacturing and machine learning-assisted process optimization.
- Ju Chan Yuk
Ph.D. candidate in the Department of Mechanical Engineering, Pusan National University. His research interests are metal-based additive manufacturing and machine learning-assisted design optimization
- Suk Hee Park
Associate Professor in the School of Mechanical Engineering, Pusan National University. His research interests are AI-assisted manufacturing and data engineering techniques