ABSTRACT
3D ground reaction force (GRF) estimation during walking is important for gait and inverse dynamics analyses. Recent studies have estimated 3D GRF based on kinematics measured from optical or inertial motion capture systems without force plate measurement. A neural network (NN) could be used to estimate ground reaction forces. The NN network approach based on segment kinematics requires the selection of optimal inputs, including kinematics type and segments. This study aimed to select optimal input kinematics for implementing an NN for each foot’s GRF estimation. A two-stage NN consisting of a temporal convolution network for gait phase detection and a gated recurrent unit network was developed for GRF estimation. To implement the NN, we conducted level/inclined walking and level running on a force-sensing treadmill, collecting datasets from seven male participants across eight experimental conditions. Results of the input selection process indicated that the center of mass acceleration among six kinematics types and trunk, pelvis, thighs, and shanks among 15 individual segments showed the highest correlations with GRFs. Among four segment combinations, the combination of trunk, thighs, and shanks demonstrated the best performance (root mean squared errors: 0.28, 0.16, and 1.15 N/kg for anterior-posterior, medial-lateral, and vertical components, respectively).
-
KEYWORDS: Ground reaction force, Segment kinematics, Neural network, Full-body dynamics
-
KEYWORDS: 지면반력, 분절 운동학, 신경망, 전신 역학
1. Introduction
Ground reaction forces (GRFs) play a crucial role in biomechanics, sports science, and rehabilitation engineering. It provides essential insights into human movement dynamics, enabling the analysis of joint loading [
1], gait abnormalities [
2], and musculoskeletal function [
3]. The accurate estimation of GRF is fundamental in various applications, including joint reaction force and torque estimation [
4-
6], and the development of exoskeletons for assistive and rehabilitative purposes [
7-
9]. Traditional GRF measurement relies on force plates, which, while highly accurate, are limited by their spatial constraints and high cost. Consequently, alternative methods for estimating GRF using kinematic data have gained increasing attention.
One promising approach for GRF estimation without force plate measurements is inverse dynamics. Inverse dynamics is a widely used approach for estimating joint reaction forces and torques by employing kinematic data and external forces. This method utilizes Newton-Euler equations to estimate forces and moments acting on the body during locomotion [
10-
12]. By applying top-down inverse dynamics, which propagate forces from the free ends, such as the head or hands, where no external force is applied, GRFs can be estimated from full-body segment kinematics without the need for direct force measurements. In this study, this approach will be referred to as full-body dynamics (FBD).
Various studies have explored GRF estimation using segment kinematics. Early research predominantly relied on optical motion capture (OMC) systems, which provide full-body segment kinematics with high accuracy by tracking reflective markers attached to anatomical landmarks [
13-
15]. OMC-based GRF estimation has been validated against force plate measurements and has demonstrated promising results. However, its dependence on laboratory settings and expensive equipment limits its applicability in real-world scenarios.
To address these limitations, inertial motion capture (IMC) systems have emerged as a viable alternative for GRF estimation [
16]. IMC systems utilize inertial measurement units (IMUs) attached to full-body segments to capture segment kinematics in outside-the-laboratory environments such as outdoor settings [
17,
18]. Recent studies have shown that IMC-based GRF estimation, combined with inverse dynamics [
19-
22] or machine learning models [
23-
26], can achieve reasonable accuracy while providing greater flexibility compared to OMC systems. Despite the advancements in GRF estimation using kinematic data, challenges remain in achieving high accuracy across different locomotion conditions, such as walking and running at various speeds and inclines.
As a plot study on IMC-based GRF estimation, this study aims to implement a neural network model for GRF estimation based on optimal segment kinematics input from the OMC system. In this regard, this study selects kinematics types and segments that have a high correlation with GRF and identifies the optimal segment combination through a comparison of different segment combinations.
2. Method
The purpose of this study is to implement a neural network model that estimates the 3D GRF of both feet during walking and running based on optimal segment kinematics. This section describes the FBD approach and the neural network approach for GRF estimation, as well as the procedure for selecting the optimal inputs for the neural network approach.
2.1 Full-Body Dynamics Approach
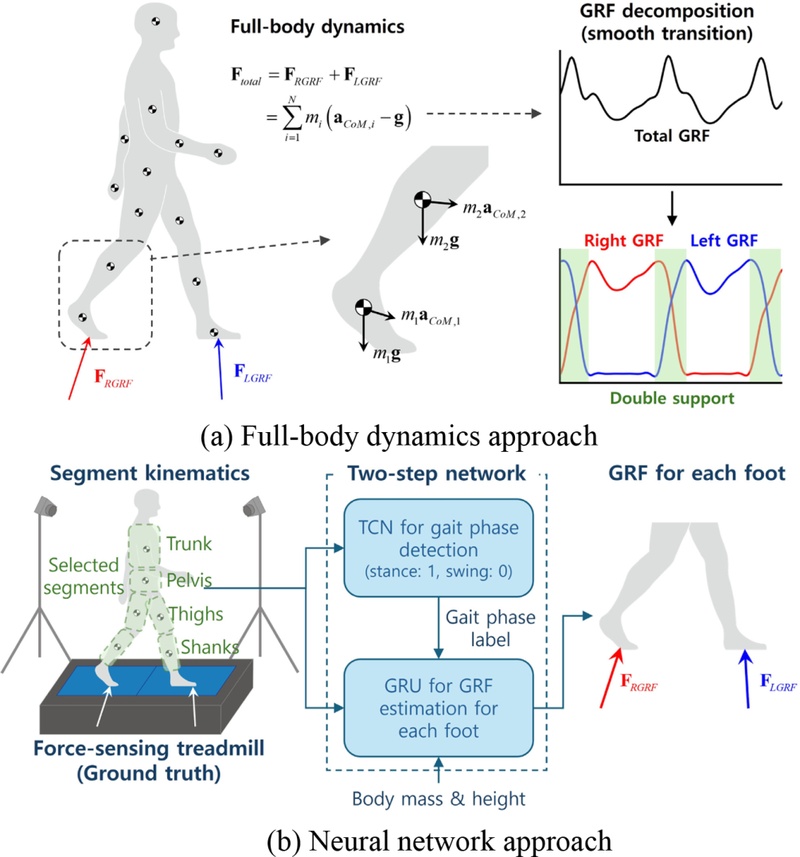
The FBD calculates GRFs based on the center-of-mass (CoM) acceleration of the full-body segments using Newton's equations of motion as follows (See
Fig. 1(a)):
Fig. 1Concept of the GRF estimation for each foot: (a) Full-body dynamics and (b) Neural network approaches
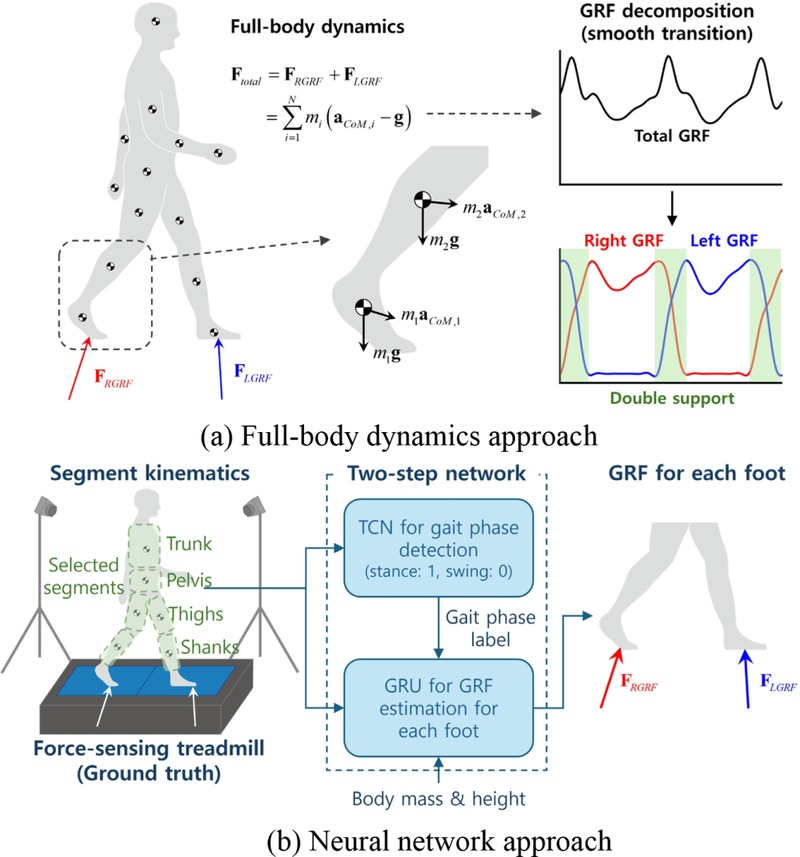
Where N is the number of full-body segments, mi is the mass of the i-th segment, aCoM,i is the CoM acceleration vector of the i-th segment, and g is the gravitational acceleration vector.
In the single support phase, where only one foot is in contact with the ground, each foot's GRF is clearly determined. However, in the double support phase, where both feet are in contact with the ground simultaneously, the GRF estimation becomes an underdetermined problem. To solve this problem, a decomposition technique based on the smooth transition assumption has been developed [
13].
The neural network approach estimates GRFs using a model that learns the correlation between segment kinematics and GRFs measured from force platforms. In estimating the GRFs of both feet, the gait phase of each foot is crucial information, as it indicates whether the movement is in a single or double support phase. Therefore, this study develops a two-stage neural network model consisting of a network for gait phase detection and a network for GRF estimation (See
Fig. 1(b)). As neural network types, we employed a temporal convolution network (TCN) [
27] for gait phase detection and a gated recurrent unit (GRU) [
28], a variant of recurrent neural network (RNN), for GRF estimation, both designed for processing long-term time-series data. For gait phase detection and GRF estimation, each network was empirically selected based on a comparative evaluation of long short-term memory, GRU, and TCN architectures.
The first network estimates the gait phase labels (1 for stance phase and 0 for swing phase) of both feet, enabling the distinction between single and double support phases. The network is designed to take accelerations and angular velocities from the lower limb segments as input through a 1D dilated causal convolution with a receptive field of 31 time steps (0.31 seconds at 100 Hz). The hidden layers consist of multiple dilated convolutional layers with a kernel size of 3, a channel size of 50, and 4 convolutional channels. After passing through these convolutional layers, the final output is processed through a sigmoid function to generate the gait phase labels.
The second network for estimating GRFs is designed to take the gait phase label for each foot estimated from the first network and segment kinematics at the current time step as input. These inputs pass through two GRU layers with 300 hidden units, and the resulting output, combined with the subject's body mass and height, is processed by a fully connected layer to estimate the GRF for the right and left foot at the current time step.
During the training process, inputs of the two-stage neural networks were standardized to have zero mean and a standard deviation of one, while the output of the second network, i.e., GRFs, was normalized using min-max normalization to range between 0 and 1. Each neural network was trained using truncated backpropagation through time (TBPTT), and the Ranger optimizer, which combines Rectified Adam (RAdam) [
29] and Lookahead [
30], was applied. TBPTT was performed by truncating the entire sequence of the training dataset into subsequences of 300 time steps, and then applying backpropagation through time to each subsequence. The loss functions for the first and second networks were binary cross-entropy and mean squared error, respectively. The training procedure was conducted using Fastai (2.7.17) based on the PyTorch (2.1.2) framework.
To achieve high GRF estimation performance, it is crucial to select the optimal inputs, particularly kinematics types and segments. Therefore, this study conducts the following two selection procedures: (i) First, we compare three types of translational segment kinematics—including the CoM position, velocity, and acceleration—and three types of rotational segment kinematics—including the orientation quaternion, angular velocity, and angular acceleration—to determine the most optimal input kinematics for GRF estimation; (ii) Then, we select the optimal segments from the following groups: head, trunk, pelvis, three upper limb segments (upper arms, forearms, and hands), and three lower limb segments (thighs, shanks, and feet). In the first procedure, we train neural networks based on full-body segment kinematics for each type of input kinematics and then compare the performance of the six neural networks to determine the optimal type of kinematics. In the second procedure for the selection of the optimal segments, ablation analysis was performed to evaluate the importance of each individual segment by measuring the effects of its exclusion on GRF estimation accuracy.
3. Results and Discussion
3.1 Experiment
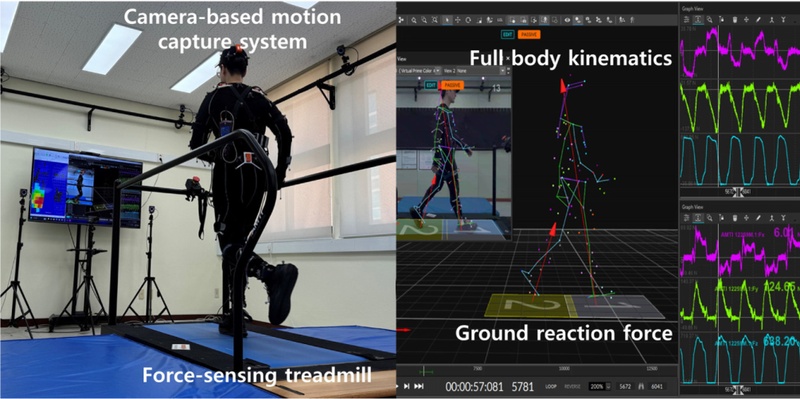
In this study, treadmill walking and running experiments were conducted to collect a dataset for the implementation of neural network models. In the experiment, seven healthy male participants (age: 24.4 ± 1.7 years, height: 1.73 ± 0.06 m, weight: 72.8 ± 6.3 kg) were recruited. The participants performed walking and running tests under the following eight conditions: level/inclined walking at two speeds (4 and 6 KPH) on three inclines (0, 3, and 6%) and level running at two speeds (7.5 and 9 KPH). For each experimental condition, the test was repeated for two trials. The study protocol was approved by the Public Institutional Review Board of the Ministry of Health and Welfare of Korea (P01-202110-13-001).
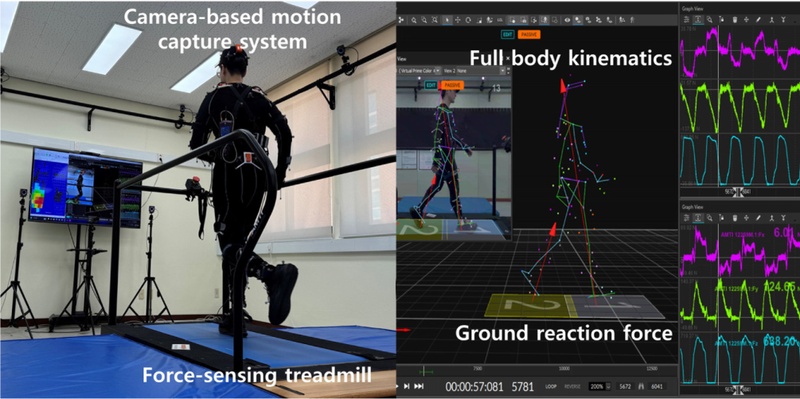
An OMC system, OptiTrack Prime 13W (NaturalPoint, Corvallis, OR, USA), was used to measure the 3D trajectory of 39 reflective markers attached to the anatomical landmarks across the entire body of each participant. The placement of the reflective markers was determined based on the Conventional Gait Model [
31]. A front-to-back split belt instrumented treadmill (AMTI, Watertown, MA, USA) was used to measure 3D GRFs during walking and running.
Fig. 2 illustrates the experimental setups.
Fig. 2Experimental setups
Reflective marker trajectories and GRFs were recorded at sampling rates of 100 and 1,000 Hz, respectively, and data from the two systems were synchronized at 100 Hz. Both data were filtered through a 4th-order Butterworth low-pass filter with cut-off frequencies of 10 and 20 Hz, respectively. Based on the marker trajectories, the coordinate frames for 15 segments (head, trunk, upper arms, forearms, hands, pelvis, thighs, shanks, and feet) were defined, and the kinematics (orientation, angular velocity, angular acceleration, CoM position, velocity, and acceleration) of all 15 segments were then computed. Additionally, heel-strike and toe-off events for both feet were identified based on vertical GRF signals, and gait phase labels were generated, where 1 indicates the stance phase and 0 indicates the swing phase.
From the collected data, sequential data including full-body segment kinematics, GRFs, and gait phase labels for 50 consecutive strides were extracted for each experimental test, generating a dataset consisting of a total of 112 trial sequences (7 participants × 8 conditions × 2 trials). To validate the neural network's performance on the dataset from seven participants, the leave-one-subject-out cross-validation was conducted using participant data that the model had not encountered during training. This involves training the model using data from six participants (96 trial sequences) and then validating it using the remaining participants' data (16 trial sequences). The root mean squared error (RMSE) of the GRF normalized by the subject's body weight in N/kg was used as an evaluation metric of the GRF estimation performance.
3.2 Results
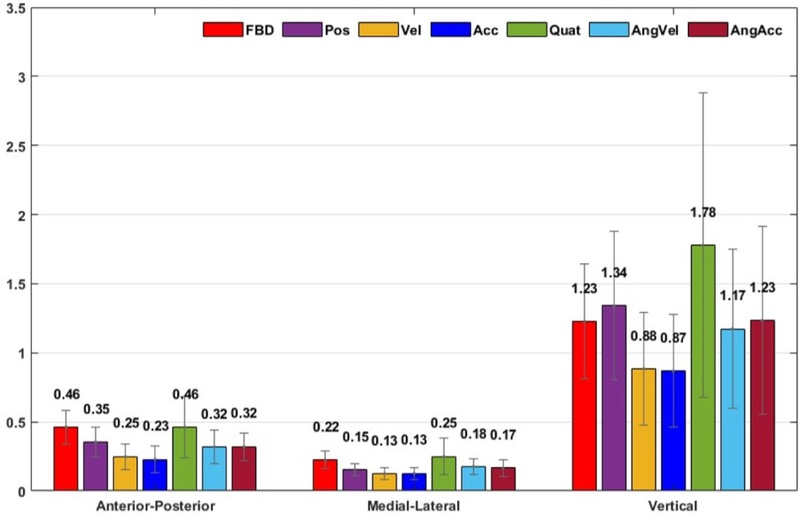
Fig. 3 presents the RMSE results of the GRF estimated from the FBD and six neural network models, each utilizing different types of input kinematics and ground truth gait phase labels as neural network input. Among the six input kinematics, CoM velocity and acceleration exhibited the best performance, with acceleration slightly outperforming velocity. Angular velocity and angular acceleration followed in performance, while CoM position and quaternion showed the weakest results, exhibiting notably larger errors than FBD for the vertical component. Since the CoM acceleration demonstrated the most optimal performance, it was selected as the input kinematics.
Fig. 3RMSE results of GRFs in N/kg for each input: Pos (position), Vel (velocity), Acc (acceleration), Quat (quaternion), AngVel (angular velocity), AngAcc (angular acceleration)
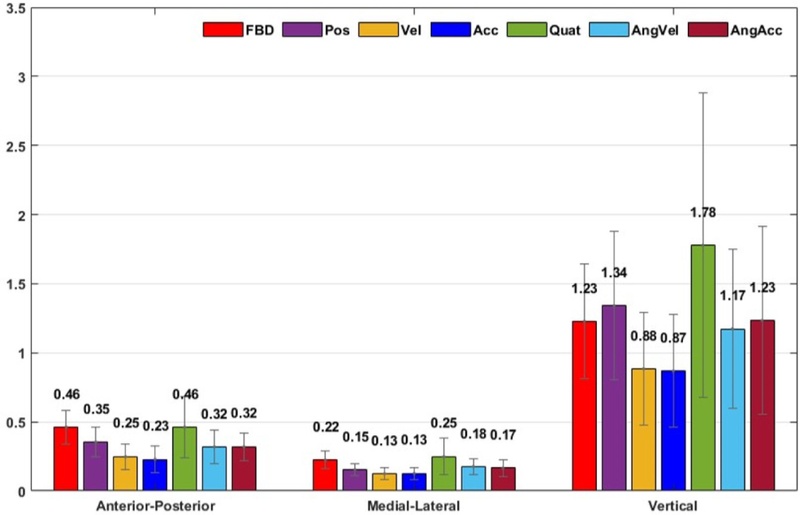
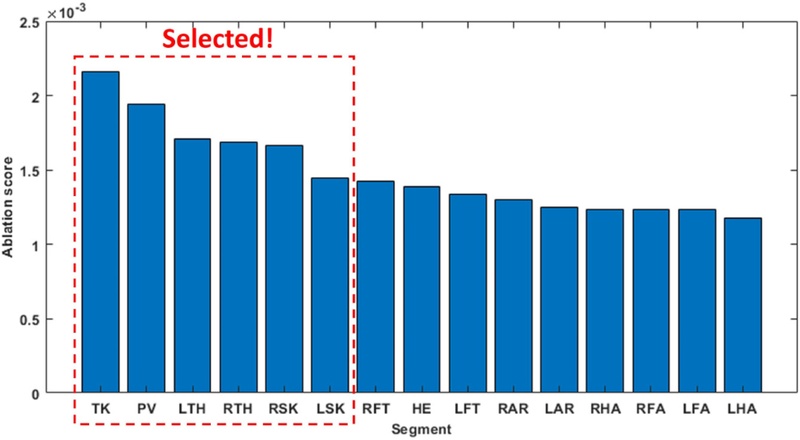
Fig. 4 presents the results of the ablation analysis for 15 individual segments. The results indicate that core segments, including the trunk and pelvis, achieved the highest scores, followed by lower limb segments such as the thighs and shanks. In contrast, the upper limb segments showed relatively lower scores. Therefore, the trunk, pelvis, and lower limb segments appear to be the most critical for GRF estimation. Among them, the trunk (TK), pelvis (PV), thighs (TH), and shanks (SK) were selected as optimal segment candidates. In addition, the thighs and shanks, which are lower limb segments, were selected as segments for gait phase detection.
Fig. 4Ablation analysis results for 15 individual segments
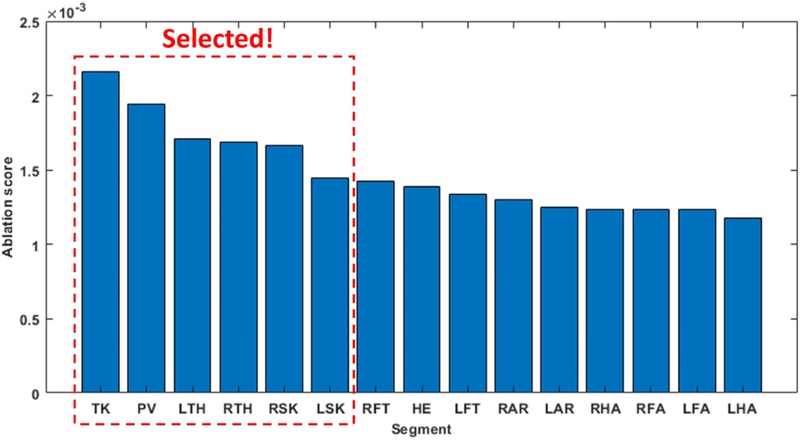
Table 1 shows the average stride time and the mean absolute error (MAE) results (in milliseconds) of the heel-strike (the transition from swing to stance phase) and toe-off (the transition from stance to swing phase) detected by the TCN based on the kinematics of the thighs and shanks for eight experimental conditions. In terms of MAE, the detection errors of heel-strike and toe-off were within 20 ms on average for all experimental conditions.
Table 1Average stride time and mean absolute errors (with standard deviations) of heel-strike and toe-off detection time
Table 1
|
Speed [KPH] |
Incline [%] |
Stride time [ms] |
Heel-strike [ms] |
Toe-off [ms] |
|
4.0 |
0 |
1138 ± 50 |
15 ± 11 |
16 ± 8 |
|
4.0 |
3 |
1166 ± 46 |
16 ± 8 |
14 ± 6 |
|
4.0 |
6 |
1196 ± 56 |
16 ± 10 |
17 ± 10 |
|
6.0 |
0 |
954 ± 69 |
14 ± 8 |
13 ± 7 |
|
6.0 |
3 |
939 ± 27 |
16 ± 10 |
15 ± 8 |
|
6.0 |
6 |
937 ± 28 |
17 ± 11 |
15 ± 10 |
|
7.5 |
0 |
735 ± 20 |
16 ± 7 |
19 ± 12 |
|
9.0 |
0 |
697 ± 23 |
18 ± 6 |
15 ± 7 |
Based on the segments selected from the ablation analysis results (
Fig. 4),
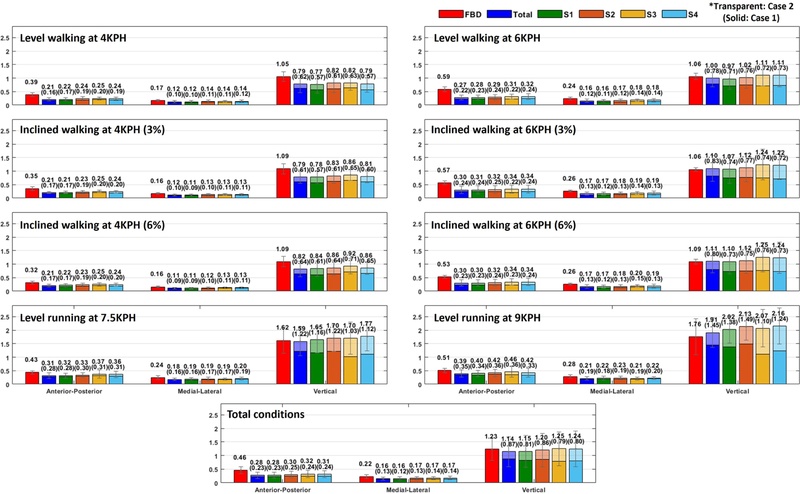
Fig. 5 presents the RMSE of the GRF estimated from the FBD and five neural network models, each based on different segment combinations, under eight experimental conditions. The following four segment combinations were compared along with the model using total segments (Total): (S1) TK+TH+SK; (S2) PV+TH+SK; (S3) TK; and (S4) PV. Additionally, to analyze the effect of gait phase detection accuracy, two cases were compared: (Case 1) one using ground truth gait phase labels (solid color) and (Case 2) the other using estimated gait phase labels (transparent color).
Fig. 5RMSE results of GRFs in N/kg under eight experimental conditions and on average for different segment combinations: Total (15 segments), S1 (trunk, thighs, shanks), S2 (pelvis, thighs, shanks), S3 (trunk), S4 (pelvis)
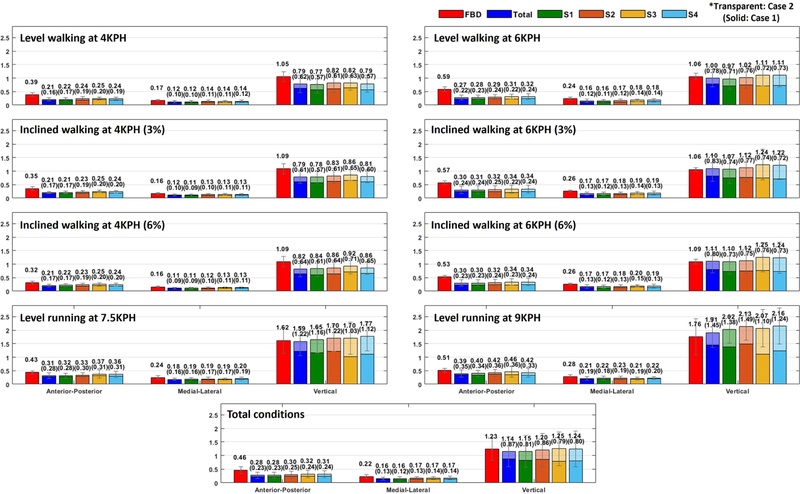
For the anterior-posterior (AP) and medial-lateral (ML) components, the FBD approach resulted in the highest RMSE, while the neural network approach showed reduced errors, which were particularly pronounced during walking at 6 KPH. When comparing different segment combinations, the performance differences were negligible; however, on average, S1 showed a slight advantage and demonstrated performance comparable to Total. Additionally, using the estimated gait phase was found to cause an RMSE increase of within 0.1 N/kg compared to using the ground truth.
For the vertical component, the performance difference between the FBD and neural network approaches varied depending on speed and gait phase type. In Case 1, the neural network for all segment combinations outperformed the FBD across all experimental conditions. In Case 2, the neural network approach showed lower RMSEs than the FBD at 4 KPH walking, whereas at 6 KPH walking and running, it exhibited RMSEs that were similar to or higher than those of the FBD. When comparing by segment combination, S1 showed a slight advantage for walking in both cases. For running, in Case 2, Total showed the best performance, followed by S1, whereas in Case 1, S3 outperformed the other combinations.
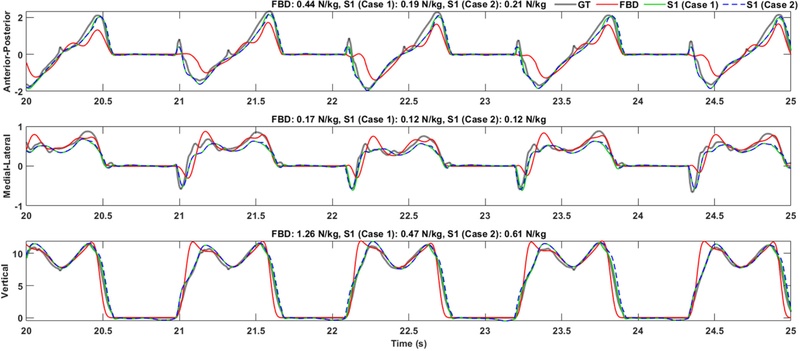
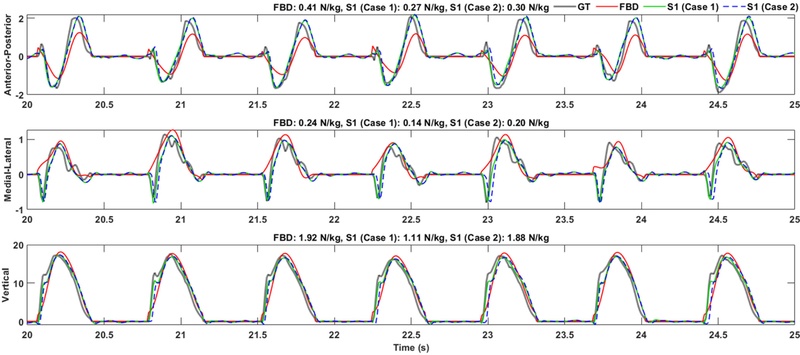
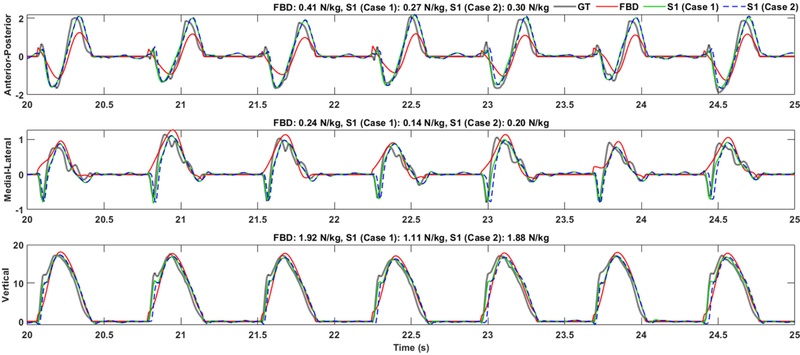
Figs. 6 and
7 present the ground truth GRF along with the GRF estimated from full-body dynamics and the neural network using segment combination S1 for Cases 1 and 2, during 4 KPH level walking and 7 KPH level running, respectively. In both walking and running results, the neural network particularly closely followed the ground truth in the AP and ML components compared to the FBD. However, a delay between the neural network results and the ground truth was observed, particularly during running. Additionally, when comparing Case 1 and Case 2, the difference between the two cases was not prominent; however, Case 2 showed a more delayed estimation than Case 1, particularly in the vertical component.
Fig. 6RMSE and estimation results of 3D GRF in N/kg during level walking at 4 KPH: ground truth (GT), full-body dynamics (FBD), neural network using segment combination S1 (Cases 1 and 2)
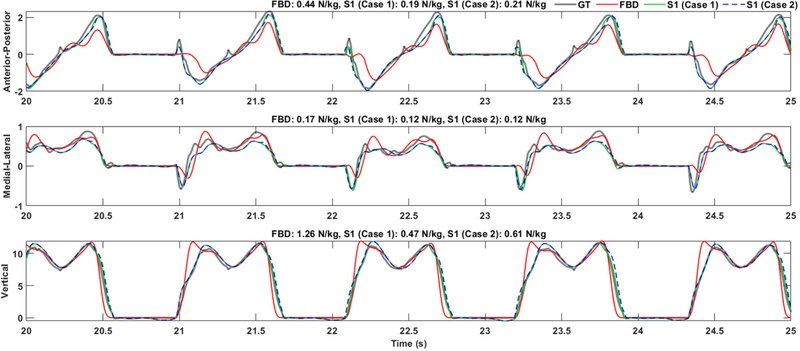
Fig. 7RMSE and estimation results of 3D GRF in N/kg during level running at 7 KPH: ground truth (GT), full-body dynamics (FBD), neural network using segment combination S1 (Cases 1 and 2)
3.3 Discussion
The previous chapter demonstrated the selection of the optimal input candidates, including kinematics types and segments, as well as the comparative results across different segment combinations for GRF estimation using a neural network.
Among the six translational and rotational kinematics, CoM acceleration demonstrated the best performance (See
Fig. 3). The full-body dynamics procedure for GRF estimation, based on Newton's equations of motion, is composed of the segment mass, segment's CoM acceleration, and gravitational acceleration. Considering this, it can be inferred that GRF is dependent on CoM acceleration, and thus it is reasonable to expect a high correlation between CoM acceleration and GRF. Angular velocity was also found to be highly correlated with GRF, suggesting that it is worth considering alongside as an additional input for kinematics. In addition, angular velocity is a crucial kinematic feature for gait phase detection, making it essential [
32]. As previously mentioned, considering that IMC-based GRF estimation will be studied in the future, it is good news that the acceleration and angular velocity are the most useful information. This is because, when using IMC, the acceleration and angular velocity are advantageous for signal acquisition compared to position, velocity, or angular acceleration. Acceleration can be extracted from accelerometer signals when the orientation information is known, and angular velocity can be directly measured through gyroscope signals. On the other hand, velocity and position are obtained by integrating acceleration, which poses a risk of boundless drift. Similarly, rotational velocity is obtained by differentiating angular velocity, making it vulnerable to noise issues.
In terms of the importance of individual segments, core segments (trunk and pelvis) had the highest importance, followed by lower limb segments (thighs and shanks), while upper limb segments showed lower importance. Considering that many studies have utilized the correlation between the human body's CoM kinematics and lower limb kinetics [
23], the trunk and pelvis can be regarded as essential segments for GRF estimation. Additionally, lower limb segments are effectively utilized for recognizing gait events of walking and running, such as heel strike and toe-off [
32], which may contribute to improving GRF estimation performance.
Comparing the four segment combinations selected in this study, a combination of trunk, thighs, and shanks (S1) demonstrated superior performance on average compared to other combinations in both Cases 1 and 2. Exceptionally, in Case 1, for running, the trunk (S3) showed the best performance, followed by the pelvis (S4). It is noteworthy that using a single core segment (S3 and S4) outperformed not only the combination of core and lower limb segments (S1 and S2) but also the use of all segments (Total). This implies that having more information may, in some cases, lead to a slight decrease in performance. Comparing S1 to Total, Total showed a slight advantage in the vertical component; however, in terms of average RMSE, the difference was 0.01 N/kg in Case 1 and 0.06 N/kg in Case 2.
In Case 2, where the estimated gait phase was used, performance significantly declined compared to Case 1, particularly in running, due to gait phase detection errors. The MAE of heel-strike and toe-off detection times in
Table 1 was within 20 ms across all experimental conditions, which corresponds to two samples at a 100 Hz sampling rate. However, considering that stride time shortens as speed increases, a small gait phase detection error—even as little as 20 ms—is expected to have a greater impact on GRF estimation performance at higher speeds. Therefore, the performance of gait detection plays a crucial role in the accuracy of GRF estimation in the neural network approach. To quantitatively investigate the impact of gait detection accuracy on GRF estimation performance,
Table 2 presents the RMSEs of the Total model under gait detection time offsets of 0, ±10, ±20, and ±30 ms. As the time offset increased from 0 to +30 ms, the RMSE increased by 0.10, 0.05, and 0.47 N/kg for the anterior-posterior, medial-lateral, and vertical components, respectively. In addition, as the time offset decreased from 0 to -30 ms, the RMSE increased by 0.05, 0.04, and 0.37 N/kg for the three components, respectively. The results indicate that GRF estimation performance—particularly in the vertical component—is sensitive to the gait phase detection error, with larger error increases observed for positive time offsets (i.e., delayed detection) compared to negative ones (i.e., early detection).
Table 2RMSE results of GRFs in N/kg from neural network using total segments according to the gait detection time offset
Table 2
|
Time offset [ms] |
Anterior-Posterior |
Medial-Lateral |
Vertical |
|
0 |
0.23 |
0.13 |
0.87 |
|
+10/−10 |
0.24/0.24 |
0.13/0.14 |
0.93/0.94 |
|
+20/−20 |
0.28/0.26 |
0.15/0.15 |
1.11/1.09 |
|
+30/−30 |
0.32/0.28 |
0.18/0.16 |
1.34/1.24 |
As a pilot study for GRF estimation based on an IMC system, this work is limited by the small number of participants (seven males) and experimental conditions (eight conditions), as well as the exclusive use of an OMC system. In future studies, a more diverse range of participants—across gender, age, and body type—as well as a broader set of experimental conditions (e.g., running at higher speeds above 10 KPH) will be included to improve the generalizability of the model. In the experiment, IMC system data will be collected alongside other measurements, with IMUs attached to 17 body segments according to the full-body sensor setup of the Xsens MVN system [
21]. Once the dataset collection is completed, we plan to apply techniques such as saliency maps and SHAP values to identify the features and segments that significantly contribute to GRF estimation performance, and subsequently develop a GRF estimation model based on the IMC dataset. The performance of the developed model will be investigated in more detail across different locomotion conditions (e.g., speed and incline). Moreover, to enhance model performance, future work will identify key challenges, such as IMU-based orientation estimation errors [
17,
18] and sensor-to-segment misalignment [
33]—that may arise when using IMU-based segment kinematics as model inputs, and apply appropriate solutions to address them.
4. Conclusion
The purpose of this study is to implement a neural network for estimating each foot's GRF during walking and running based on segment kinematics. To achieve this, the optimal input kinematics and segments were selected. The neural network designed in this study consists of a TCN for gait phase detection and a GRU network for GRF estimation. In the results, (i) six types of translational and rotational kinematics, (ii) 15 individual segments, and (iii) four segment combinations, along with two gait detection types (ground truth and estimated), were analyzed and compared. First, CoM acceleration demonstrated the best performance and was therefore selected as the input kinematics type. Second, among the 15 individual segments, trunk, pelvis, thighs, and shanks, in order, showed the highest importance, and these were selected as the segment candidates. Third, the combination of trunk, thighs, and shanks (S1) demonstrated the best performance across all conditions among the four segment combinations. However, when using the estimated gait phase (Case 2), the RMSE of the GRF for AP, ML, and vertical components increased by 0.05, 0.04, and 0.34 N/kg, respectively, compared to using the ground truth gait phase (Case 1).
This study serves as a preliminary investigation into GRF estimation using inertial motion capture, implementing a neural network for GRF estimation based on segment kinematics measured from OMC system. The main contribution of this study lies in identifying informative segment kinematics and body segments for GRF estimation while walking under various speeds and inclines. In our future research, we plan to replace the OMC system with the IMC system, thereby developing a model trained on IMC datasets and identifying the most informative body segments, i.e., the IMU attachment locations, for accurate IMC-based GRF estimation. Additionally, we aim to develop a neural network that can automatically estimate GRF for each foot without the need for gait phase detection.
REFERENCES
- 1.
Shelburne, K. B., Torry, M. R., Pandy, M. G., (2006), Contributions of muscles, ligaments, and the ground-reaction force to tibiofemoral joint loading during normal gait, Journal of Orthopaedic Research, 24(10), 1983-1990.
10.1002/jor.20255
- 2.
Muniz, A. M. S., Nadal, J., (2009), Application of principal component analysis in vertical ground reaction force to discriminate normal and abnormal gait, Gait & Posture, 29(1), 31-35.
10.1016/j.gaitpost.2008.05.015
- 3.
Turns, L. J., Neptune, R. R., Kautz, S. A., (2007), Relationships between muscle activity and anteroposterior ground reaction forces in hemiparetic walking, Archives of Physical Medicine and Rehabilitation, 88(9), 1127-1135.
10.1016/j.apmr.2007.05.027
- 4.
Riemer, R., Hsiao-Wecksler, E. T., Zhang, X., (2008), Uncertainties in inverse dynamics solutions: a comprehensive analysis and an application to gait, Gait & Posture, 27(4), 578-588.
10.1016/j.gaitpost.2007.07.012
- 5.
Camomilla, V., Cereatti, A., Cutti, A. G., Fantozzi, S., Stagni, R., Vannozzi, G., (2017), Methodological factors affecting joint moments estimation in clinical gait analysis: a systematic review, Biomedical Engineering Online, 16, 1-27.
10.1186/s12938-017-0396-x
- 6.
Lee, C. J., Lee, J. K., (2022), Inertial motion capture-based wearable systems for estimation of joint kinetics: A systematic review, Sensors, 22(7), 2507.
10.3390/s22072507
- 7.
Fineberg, D. B., Asselin, P., Harel, N. Y., Agranova-Breyter, I., Kornfeld, S. D., Bauman, W. A., Spungen, A. M., (2013), Vertical ground reaction force-based analysis of powered exoskeleton-assisted walking in persons with motor-complete paraplegia, The Journal of Spinal Cord Medicine, 36(4), 313-321.
10.1179/2045772313Y.0000000126
- 8.
Azimi, V., Nguyen, T. T., Sharifi, M., Fakoorian, S. A., Simon, D., (2018), Robust ground reaction force estimation and control of lower-limb prostheses: Theory and simulation, IEEE Transactions on Systems, Man, and Cybernetics: Systems, 50(8), 3024-3035.
10.1109/TSMC.2018.2836913
- 9.
Li, H., Ju, H., Liu, J., Wang, Z., Zhang, Q., Li, X., Huang, Y., Zheng, T., Zhao, J., Zhu, Y., (2023), Ground contact force and moment estimation for human–exoskeleton systems using dynamic decoupled coordinate system and minimum energy hypothesis, Biomimetics, 8(8), 558.
10.3390/biomimetics8080558
- 10.
Winter, D. A., (2009), Biomechanics and motor control of human movement, John Wiley & Sons.
10.1002/9780470549148
- 11.
Koopman, B., Grootenboer, H. J., De Jongh, H. J., (1995), An inverse dynamics model for the analysis, reconstruction and prediction of bipedal walking, Journal of Biomechanics, 28(11), 1369-1376.
10.1016/0021-9290(94)00185-7
- 12.
Kingma, I., de Looze, M. P., Toussaint, H. M., Klijnsma, H. G., Bruijnen, T. B., (1996), Validation of a full body 3-D dynamic linked segment model, Human Movement Science, 15(6), 833-860.
10.1016/S0167-9457(96)00034-6
- 13.
Ren, L., Jones, R. K., Howard, D., (2008), Whole body inverse dynamics over a complete gait cycle based only on measured kinematics, Journal of Biomechanics, 41(12), 2750-2759.
10.1016/j.jbiomech.2008.06.001
- 14.
Iino, Y., Kojima, T., (2012), Validity of the top-down approach of inverse dynamics analysis in fast and large rotational trunk movements, Journal of Applied Biomechanics, 28(4), 420-430.
10.1123/jab.28.4.420
- 15.
Fluit, R., Andersen, M. S., Kolk, S., Verdonschot, N., Koopman, H. F., (2014), Prediction of ground reaction forces and moments during various activities of daily living, Journal of Biomechanics, 47(10), 2321-2329.
10.1016/j.jbiomech.2014.04.030
- 16.
Ancillao, A., Tedesco, S., Barton, J., O’Flynn, B., (2018), Indirect measurement of ground reaction forces and moments by means of wearable inertial sensors: A systematic review, Sensors, 18(8), 2564.
10.3390/s18082564
- 17.
Lee, J. K., Park, E. J., (2009), Minimum-order Kalman filter with vector selector for accurate estimation of human body orientation, IEEE Transactions on Robotics, 25(5), 1196-1201.
10.1109/TRO.2009.2017146
- 18.
Lee, J. K., Park, E. J., Robinovitch, S. N., (2012), Estimation of attitude and external acceleration using inertial sensor measurement during various dynamic conditions, IEEE Transactions on Instrumentation and Measurement, 61(8), 2262-2273.
10.1109/TIM.2012.2187245
- 19.
Yang, E. C. Y., Mao, M. H., (2015), 3D analysis system for estimating intersegmental forces and moments exerted on human lower limbs during walking motion, Measurement, 73, 171-179.
10.1016/j.measurement.2015.05.020
- 20.
Faber, G. S., Chang, C., Kingma, I., Dennerlein, J., Van Dieën, J., (2016), Estimating 3d l5/s1 moments and ground reaction forces during trunk bending using a full-body ambulatory inertial motion capture system, Journal of Biomechanics, 49(6), 904-912.
10.1016/j.jbiomech.2015.11.042
- 21.
Karatsidis, A., Bellusci, G., Schepers, H. M., De Zee, M., Andersen, M. S., Veltink, P. H., (2016), Estimation of ground reaction forces and moments during gait using only inertial motion capture, Sensors, 17(1), 75.
10.3390/s17010075
- 22.
Noamani, A., Nazarahari, M., Lewicke, J., Vette, A. H., Rouhani, H., (2020), Validity of using wearable inertial sensors for assessing the dynamics of standing balance, Medical Engineering & Physics, 77, 53-59.
10.1016/j.medengphy.2019.10.018
- 23.
Lee, M., Park, S., (2020), Estimation of three-dimensional lower limb kinetics data during walking using machine learning from a single IMU attached to the sacrum, Sensors, 20(21), 6277.
10.3390/s20216277
- 24.
Dorschky, E., Nitschke, M., Martindale, C. F., Van den Bogert, A. J., Koelewijn, A. D., Eskofier, B. M., (2020), CNN-based estimation of sagittal plane walking and running biomechanics from measured and simulated inertial sensor data, Frontiers in Bioengineering and Biotechnology, 8, 604.
10.3389/fbioe.2020.00604
- 25.
Johnson, W. R., Mian, A., Robinson, M. A., Verheul, J., Lloyd, D. G., Alderson, J. A., (2020), Multidimensional ground reaction forces and moments from wearable sensor accelerations via deep learning, IEEE Transactions on Biomedical Engineering, 68(1), 289-297.
10.1109/TBME.2020.3006158
- 26.
Martínez-Pascual, D., Catalán, J. M., Blanco-Ivorra, A., Sanchís, M., Arán-Ais, F., García-Aracil, N., (2023), Estimating vertical ground reaction forces during gait from lower limb kinematics and vertical acceleration using wearable inertial sensors, Frontiers in Bioengineering and Biotechnology, 11, 1199459.
10.3389/fbioe.2023.1199459
- 27.
Bai, S., Kolter, J. Z., Koltun, V., (2018), An empirical evaluation of generic convolutional and recurrent networks for sequence modeling, arXiv preprint arXiv:
1803.01271.
- 28.
Cho, K., Van Merriënboer, B., Gulcehre, C., Bahdanau, D., Bougares, F., Schwenk, H., Bengio, Y., (2014), Learning phrase representations using RNN encoder-decoder for statistical machine translation, arXiv preprint arXiv:
1406.1078.
- 29.
Liu, L., Jiang, H., He, P., Chen, W., Liu, X., Gao, J., Han, J., (2019), On the Variance of the Adaptive Learning Rate and Beyond, arXiv preprint arXiv:
1908.03265.
- 30.
Zhang, M., Lucas, J., Hinton, G., Ba, J., (2019), Lookahead Optimizer: k steps forward, 1 step back, arXiv preprint arXiv:
1907.08610.
- 31.
Baker, R., Leboeuf, F., Reay, J., Sangeux, M., (2018), The conventional gait model - success and limitations, in: handbook of human motion, Springer International Publishing, Cham, 489-508.
10.1007/978-3-319-14418-4_25
- 32.
Lee, J. K., Park, E. J., (2011), Quasi real-time gait event detection using shank-attached gyroscopes, Medical & Biological Engineering & Computing, 49, 707-712.
10.1007/s11517-011-0736-0
- 33.
Di Raimondo, G., Vanwanseele, B., Van der Have, A., Emmerzaal, J., Willems, M., Killen, B. A., Jonkers, I., (2022), Inertial sensor-to-segment calibration for accurate 3D joint angle calculation for use in OpenSim, Sensors, 22(9), 3259.
10.3390/s22093259
Biography
- Chang June Lee
Ph.D. candidate in the Department of Integrated Systems Engineering, Hankyong National University. His research interests include IMU-based human motion tracking and joint torque estimation as well as wearable robotics.
- Jung Keun Lee
Professor in the School of ICT, Robotics & Mechanical Engineering, Hankyong National University. His research interests include inertial sensing-based human motion tracking, biomechatronics, wearable sensor applications, and data-driven estimation.