ABSTRACT
This study numerically investigates the spreading and retracting dynamics of Janus drops on the inner surfaces of cylinders using the Volume of Fluid method. The results indicate that increasing surface curvature enhances spreading in the axial direction and promotes the detachment of the low-viscosity water component, particularly under conditions of high viscosity ratio and Weber number. A regime map is constructed to identify the critical conditions for separation, revealing that surfaces with intermediate curvature exhibit higher separation efficiency compared to those with high curvature. The temporal evolution of axial momenta in the x and z directions highlights the role of viscosity contrast in inducing asymmetric deformation. A scaling law for residence time is proposed as a function of Weber number, which aligns well with simulation results in the high Weber number regime. These findings provide fundamental insights for optimizing surface curvature and fluid composition to enhance drop separation and may benefit applications such as selective liquid extraction, surface cleaning, and microfluidic manipulation.
-
KEYWORDS: Janus droplet, Interfacial dynamics, Droplet bouncing, Residence time, Multiphase flow, Superhydrophobic surface
-
KEYWORDS: 야누스 액적, 계면 동역학, 액적 반동, 체류시간, 다상 유동, 초소수성 표면
1. 서론
고체 표면 위의 액적 충돌 현상은 표면 냉각[
1], 세정[
2], 농약 분사[
3], 잉크젯 프린팅[
4], 법의학적 분석[
5] 등 다양한 공학적 응용 뿐만 아니라 기초 연구 분야에서도 지속적으로 주목받고 있다. 최근에는 약물 전달, 바이오센서 등 복합 액적(Compound Drops)의 조작성 및 활용 기술과 관련된 연구가 활발히 이루어지고 있다[
6]. 복합 유체(Compound Fluid)는 일반적으로 두 개 이상의 상으로 이루어져 있으며, 다양한 산업 분야에서 널리 활용되고 있다. 이러한 유체는 생성 방식이나 물리적 특성에 따라 야누스 구조(Janus Structure), 코어-셸 구조(Core-shell Structure) 등으로 분류될 수 있다[
7]. 특히 동적 충돌 조건에서, 야누스 액적은 다상(Multi-phase) 특성에 기인하여 단상(Single-phase) 유체와는 다른 독특한 거동을 나타낼 수 있다. 예를 들어, 고점도 유체와 저점도 유체가 조합된 야누스 액적의 경우, 서로 다른 점성 특성으로 인해 구조적 안정성이 확보되는 것으로 나타났다[
8]. 또한, 저점도 성분은 복합 액적의 구성 및 형상에 따라 스플래싱(Splashing) 현상을 선택적으로 강화하거나 억제하는 조절 인자로 작용할 수 있음이 보고되었다. 최근에 본 연구팀은 평면[
9], 볼록한 표면[
10]에서 야누스 액적의 분리 효율(Ω) 증가 및 체류시간 감소 가능성을 입증하였다. 이 외에 이방성 표면(Anisotropic Surfaces) 위에서의 복합 액적 충돌 거동에 대한 많은 연구는 이루어지지 않았으며, 해당 조건이 충돌 역학을 능동적으로 제어할 수 있는 가능성에 대해서도 충분히 탐구되지 않았다. 평탄한 표면에서는 퍼짐 및 수축이 대체로 대칭성을 따르는 제한적인 범위 내에서 이루어지기 때문에, 구조적 비대칭성과 복합 액적의 물성 조합이 결합된 조건에서의 동역학 변화는 향후 연구가 필요한 핵심 주제라 할 수 있다.
액적의 반동 거동은 접촉 시간 최소화와 에너지 손실 억제 등의 특이한 물리적 특성으로 인해 표면과학 분야에서 활발한 관심을 받고 있다[
11]. 액적이 표면에서 머무는 시간을 최소화하는 것은 액적과 표면 간 상호작용에서 질량, 운동량, 에너지 전달 효율성을 평가하는 주요 지표로 작용하며, 일반적으로 관성–표면장력 시간의 스케일링
τ0∼ρD03/8σ1/2를 기준으로 근사된다. 여기서
ρ,
D0,
σ는 각각 밀도, 액적 지름, 표면장력을 의미한다. 충돌 동역학 특성을 특성화하기 위해서는 Weber (
We), Reynolds (
Re), Ohnesorge (
Oh) 수 등 여러 무차원 수들이 사용되며, 이들은 각각 다음과 같이 정의된다:
We=ρD0V02/σ (관성력 대비 표면장력),
Re=ρD0V0/μ (관성력 대비 점성력),
Oh=We1/2/Re (점성력 대비 관성 및 표면장력). 여기서
V0는 충돌 속도,
μ는 액체의 점도이다.
곡면 위의 액적 충돌 현상의 연구는 거동 및 체류시간을 크게 변화시킬 수 있다. 하지만 대부분의 연구는 충돌하는 표면이 볼록한 경우에 대하여 실험적, 수치적인 분석이 진행되었고, 오목한 경우는 고온표면에 대한 연구가 주로 수행되었다. Han 등[
12]은 볼록한 원통면 위에서의 비대칭 퍼짐이 액적 직경과 곡률 직경의 비율에 따라 결정된다는 가설을 제안하였다. 또한 실험적으로 측정된 접촉 시간을 정량적으로 예측할 수 있는 체류시간 모델을 제시하였다. Liu 등[
13]은 볼록한 다육식물 잎 위에서의 액적 충돌 시 발생하는 비대칭적인 반동 거동을 실험적으로 입증하였으며, 오목한 곡면에서의 액적 충돌에 대해서 체류 시간이 감소하는 기초실험결과를 도출하였다. Regulagadda 등[
14]은 욕조(Bathtub) 형태의 표면 위에서 액적 충돌 실험을 수행하였으며, 접선 운동량이나 비원형 자취가 없음에도 불구하고 비대칭적 거동이 유도될 수 있음을 보였다. Zhang 등[
15]은 서로 다른 온도를 가진 오목한 곡면 위에 물방울이 충돌하고 어는 과정을 실험적으로 관찰한 결과를 보고하였다. 물방울의 충돌 과정에서 원주방향으로의 최대 접촉 직경은 축 방향에 비해 작게 나타났으며, 이는 곡면 형상에 따른 비대칭 퍼짐 특성을 나타낸 것이다. Rajesh 등[
16]은 비대칭 곡률을 갖는 초 가열(Superheated) 표면에서의 충돌 동역학을 실험적으로 조사하였고, 오목 표면에서 접촉 시간이 감소하는 양상이 관찰되었는데, 이는 곡면 형상에 따른 반동 강화 및 중심 수축 유도 효과 때문인 것으로 해석하였다. Jowkar와 Morad [
17]는 고온의 반원통형 오목 곡면 위에서의 표면 온도 변화에 따른 액적 반동 높이 거동 특성을 분석하였고 비대칭 변형에 의한 반동 억제 현상에 대하여 논의하였다.
오목한 표면 위 야누스 액적의 분리는 기존의 볼록한 표면 결과[
10]와 비교하여 곡면을 이동하는 액막 변형 메커니즘이 다르다. 두 경우 곡면 형상에 의거하여 초기 접선 운동량이 존재하지만, 액적의 전체적인 진화 과정이 볼록한 표면은 액적이 원주방향으로 퍼지는 과정이라고 한다면, 오목한 표면은 액적이 축 방향으로 퍼지는 과정이라고 할 수 있다. 따라서 볼록한 표면 위의 축 방향의 수축현상이 중요하고, 오목한 표면 위에서는 원주방향의 수축 과정이 중요하다. 여기서 볼록한 표면에 충돌하는 경우, 곡면에 의한 코안다(Coandă) 효과에 의한 압력 차이로 수축 과정을 제시할 수 있지만[
10,
12], 오목한 표면 위 코안다 효과는 매우 약하게 작용하므로, 곡면 액막에 작용하는 유동 구속 효과에 의한 압력 차이로 이 과정을 제시하였다. 또한 선행 결과[
10]에서 곡률에 따른 분리효율을 조사하지 않았지만, 본 연구에서 곡률과 Weber 수에 따른 분리효율을 조사하였다. 최근의 산업기술 발전에도 불구하고, 볼록 및 오목한 곡면이 반복되는 주름 표면(Corrugated Surface)에서의 복합 액적(Compound Drops) 충돌 동역학은 여전히 충분히 규명되지 않았으며, 야누스 액적의 산업적 응용을 고려할 때 곡률과 점도비가 분리 및 반동 거동에 미치는 영향을 보다 심도 있게 규명할 필요가 있다.
본 연구는 오목한 곡률을 갖는 원통형 표면 위에서 야누스 액적이 충돌할 때 나타나는 동적 거동을 수치적으로 분석하였다. 이를 통해 실린더 곡률과 액적 직경의 비율(
d/
D0), 물 성분의 Weber 수(
Wew), 그리고 두 유체 간 점도비(
α)가 액적의 변형, 분리 여부, 및 반동 거동에 미치는 영향을 정량적으로 규명하고자 한다.
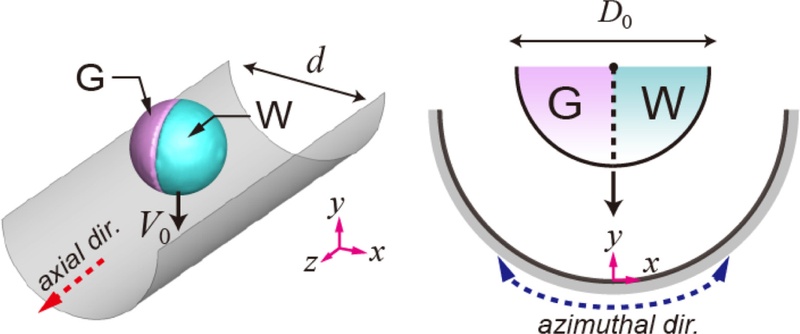
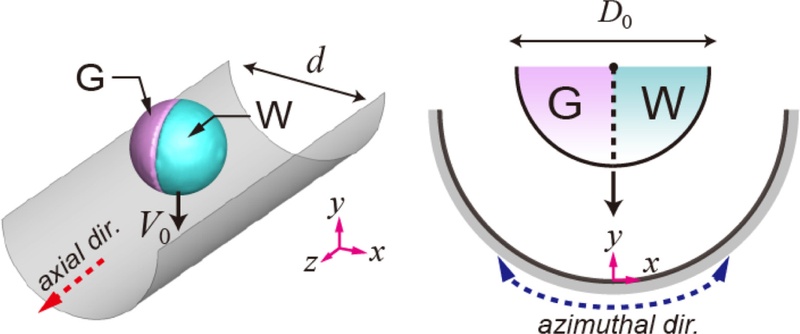
Fig. 1과 같이, 야누스 액적은 저점도 유체(W 성분)과 고점도 유체(G 성분)으로 구성되며, 이들 사이의 계면은 곡면의 축 방향과 평행으로 배치되도록 설정하였다. 본 연구는 Volume of Fluid (VOF) 기법을 적용한 수치 해석을 통해, 본 연구는 무차원 인자들의 함수로서 분리/비분리 전이 경계에 대한 상태도를 도출하고, 이러한 인자들이 액적 형상 및 운동량의 시간에 따른 변화에 어떠한 영향을 미치는지 분석하였다. 또한, W 및 G 성분의 운동량 분석과 체류시간의 스케일링 해석을 통해 액적의 비대칭 동역학이 전체 반동 거동에 미치는 영향을 규명하였다.
Fig. 1 Janus drop impact on cylindrical surfaces with a normalized diameter of d/D0. Janus drops contain W (Water) and G (Glycerin-water mixture) parts, patched with the impact velocity of V0 and outer diameter of D0 in the domain
2. Numerical Methods
본 연구에서는 곡면 위에서의 야누스 액적의 동적 특성을 예측하기 위해 VOF 기법[
18]을 적용하였다. 비압축성 3차원 질량 및 운동량 방정식은 다음과 같이 연계되어 계산 영역에 적용되었다.
여기서 밀도는
ρ=∑i=13ψiρi, 점도는
μ=∑i=13ψiμi로 정의되며,
ψi는 해당 상의 체적 분율을 의미하고
∑i=13ψi=1을 만족한다. 곡률은
κ=-∇⋅n→이며,
n→은 계면의 단위 법선 벡터이다. 계산에서는 상온 및 대기압 조건 하에서 물(저점도 유체), 글리세린/물 혼합물(고점도 유체), 공기(주위 기체) 총 세 가지 상을 고려하였다. 계면 추적은 Rider와 Kothe의 방법을 기반으로 하였으며[
19], 표면장력 항은 연속 표면력 모델(Continuous Surface Force Model)에 기반하여 근사 계산되었다[
20]. 체적 분율
ψi는 다음의 이동 방정식으로 계산되었다:
∂ψi/∂t+∇⋅ψiv→=0. 공간 및 시간 미분 항은 각각 QUICK 이산화 기법[
21] 및 1차 암시적(Implicit) 시간 적분법을 사용하여 계산되었다. 운동량 방정식 내 압력–속도 결합 문제는 PISO (Pressure-implicit with Splitting of Operator) 알고리즘을 통해 해결되었으며, 속도 및 압력장의 수렴을 향상시키기 위해 정규화 잔차 기준을 10
-5 이하로 설정하였다. 시간 간격은 1 μs 이하, 한 타임스텝 내 최대 반복 횟수는 30로 설정하였다. 격자 해상도는 액적 평형 지름 기준으로 최소 45셀 이상을 확보하였고,
d/
D0 = 2.0-8.0의 원통형 채널 조건에서 계산이 수행되었다. 원통 표면 인근에서는 계산 정확도를 높이기 위해 격자를 자가 적응적으로 밀집시켰으며, 곡면 표면 조건에서 부채꼴 형태로 계산도메인에서 해석을 수행하였다. W 및 G 성분의 물성치는
Table 1에 나타냈으며, G 성분은 서로 다른 중량비를 가지는 글리세린/물 혼합물로 구성되었다. W 및 G 성분 모두에 대해 정적 접촉각은 160°로 설정하였는데, 이는 전진각과 후퇴각이 유사하며 접촉각 이력이 4° 이하인 조건을 반영한 것이다.
Table 1 Material properties of W- and G-parts
Table 1
|
Component |
Liquid |
ρ
[kg/m3] |
μ
[Pa s] |
σ
[N/m] |
Viscosity ratio (α)
(μg / μw) [-] |
Oh
[-] |
|
W |
Water |
998.2 |
0.001 |
0.072 |
- |
0.003 |
|
G |
Glycerin/water (75 wt %) |
1185 |
0.0339 |
0.064 |
33.9 (α1)
|
0.098 |
|
Glycerin/water (80 wt %) |
1200 |
0.0549 |
0.064 |
54.9 (α2)
|
0.16 |
|
Glycerin/water (85 wt %) |
1210 |
0.0977 |
0.064 |
97.7 (α3)
|
0.28 |
|
Glycerin/water (90 wt %) |
1235 |
0.236 |
0.064 |
236 (α4)
|
0.67 |
W 및 G 성분은 각각 초기 충돌속도 및 물성치를 가지고 계산 도메인에 초기조건으로 부여되었다. W 및 G 성분 간 확산 길이는 액적 크기에 비해 매우 짧아, 액적은 실질적으로 두 유체계(Two-fluid System)로 간주할 수 있다[
8]. 두 성분 간 점도비(
α=
μg/
μw)는
α1-
α4의 네 조건으로 구분되며, 각 조건은
Table 1에 명시되어 있다. 하첨자
w 및
g는 각각 W 및 G 성분의 물리량을 지칭한다.
저점도 성분(W)의 충돌 거동은 관성–표면장력 지배 영역 (Inertial-capillary Regime)에 해당되며, 이때 무차원 수는
Wew=ρwDwV02/σw=16-75,Ohw=μw/ρwDwσw1/2=0.003이다. 여기서
Dw는 W 성분의 평형 지름이며,
D0=21/3Dw=2.0 mm를 만족한다. 고점도 성분(G)의 경우,
Ohg = 0.098-0.67로, 점성력이 동역학적 특성에 중요한 역할을 하는 조건임을 나타낸다.
Fig. 1은 직경이
d인 원통 표면 위에서 야누스 액적이 충돌하는 개략도를 나타내며,
dn은
n =
d/
D0 = 2-8를 만족하는 오목한 표면을 의미한다. 분리효율(Ω)은 충돌 후 분리된 물의 체적이 초기 체적에 대해 차지하는 비율로 정의된다. 무차원 축 방향 운동량
p는 다음과 같이 표현되며, 이는 초기 운동량에 대한
x축 또는
z축 축 방향 운동량의 상대 비로 나타난다.
여기서 vx는 x 방향 속도 성분, sgn(x)는 부호 함수이며, Di는 특정 상(phase)의 평형 지름이다. 체류시간 tc는 액적이 기판과 접촉하는 시점부터 완전히 이탈할 때까지의 지속 시간으로 정의된다.
Fig. 2는 본 연구에서 사용한 수치 모델의 타당성을 동일 조건 하에서 검증한 결과를 보여준다. 선행 연구[
14]에서 수행된 실험으로부터 얻은 단상 물방울의 연속 스냅샷을 보면, 충돌한 액적은 비대칭적인 퍼짐과 수축 과정을 거친 후 반동하는 거동을 나타낸다. 본 연구의 수치 시뮬레이션 결과는 이러한 실험 관찰과 잘 부합하며, 특히 표면 형상에 의해 유도되는 축 방향 액적 정렬 유동과 그에 따른 비대칭적 반동 특성이 재현되었다. 이를 통해 본 연구에서 제안된 수치 모델이 액적 충돌 현상을 효과적으로 모사할 수 있음을 확인할 수 있다.
Fig. 2 Model validation. Comparison of the spreading and retraction dynamics of a single-phase water drop obtained from (a) experiments (side- and top-views) and (b) current model, reprinted [14]; licensed under a Creative Commons Attribution (CC BY) license (Adapted from Ref. 14 on the basis of OA)

3. Results and Discussions
표면 곡률이 야누스 액적의 퍼짐 및 수축 거동에 미치는 영향을 알아보기 위하여, 평평한 표면과
D0/
d가 각각 1/8, 1/6, 1/2인 표면에서 반동 거동을 조사하였다.
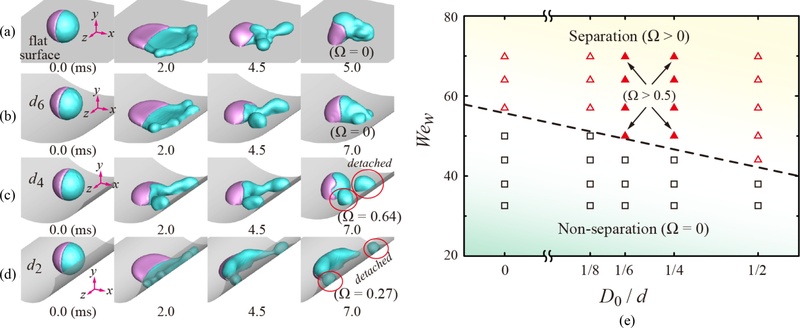
Figs. 3(a)-3(d)는 초기 직경이 동일한 야누스 액적이 서로 다른 곡률을 갖는 표면에 충돌하는 동적 거동을 시간에 따라 나타낸 그림이다. 모든 경우에서
Wew = 50과
α =
α3로 고정되었다. 여기서 곡률이 커질수록 액적의 동적 비대칭이 커지고 분리 가능성이 높아짐을 예상하였다. 평면 표면에서는 W 및 G 성분의 퍼짐 및 수축 현상의 차이가 나타났지만 W 성분은 액적 중심방향으로 수축하면서 분리는 발생하지 않았다(
Fig. 3(a), 5.0 ms). 곡률이 증가함에 따라, 저점도 성분인 W 성분은 중심에서 바깥 방향(z축 방향)으로 더욱 뚜렷하게 퍼지는 현상이 관찰되었다. 곡면의 축방향으로의 퍼짐이 강화되었고,
d4 표면에서는 W 성분의 분리 경향이 나타나기 시작하였다(Ω = 0.64). 반면
d6 표면은 평평한 표면에서의 거동 차이가 크지 않았고 W 성분은 수축현상에서 큰 액적 뭉침 현상이 발생하였다. 따라서 중간 곡률(
d4) 표면 이상의 기하학적 비대칭 표면에서 액적 분리가 크게 나타날 것으로 보인다. 가장 큰 곡률을 가지는
d2 표면에서는 액적 거동의 비대칭성이 극대화되어, W 성분이 G 성분으로부터 분리되는 현상이 명확하게 관찰되었다(
Fig. 3(d)). 이는 곡률이 클수록 곡면의 축 방향과 원주 방향으로의 퍼짐이 비대칭적으로 일어나고, 이 후 축 방향의 수축보다 원주방향의 수축이 강하게 발생하여 W 성분 양 끝 점에서 분리 거동이 유도되었기 때문이다.
d2 표면에서는 중간 곡률에서 관찰되었던 절반 이상(Ω > 0.5)의 분리효율은 관찰되지 않았고 상대적으로 낮은 분리효율을 얻었다(Ω = 0.27).
Fig. 3 Effect of the surface curvature on the spreading and retracting behavior. (a-d) Dynamic behavior of Janus drops (D0 = 2 mm) on flat, d6, d4, and d2 surfaces at Wew = 50 and α = α3, respectively, and (e) Regime map for the threshold of separation as a function of Wew and D0/d under the viscosity ratio of α4. Rectangle and triangle symbols in (e) represent W part’s non-separation and separation (open triangle: Ω ≤ 0.5; filled triangle: Ω > 0.5) cases from mother drops, respectively
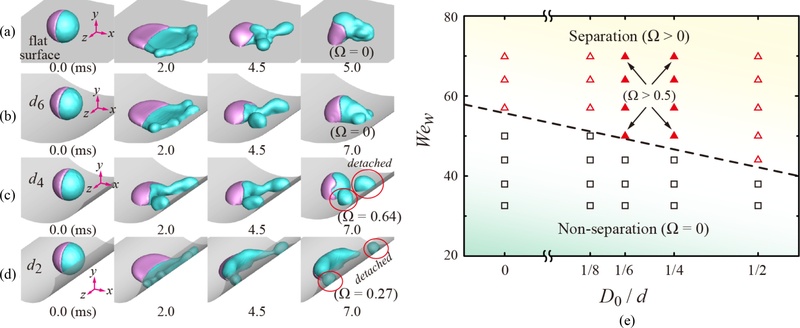
Fig. 3(e)는 야누스 액적의 충돌 시 표면 곡률에 따른 액적의 분리를 위한 임계조건을 Weber 수와 곡률직경비(
D0/
d)에 따라 조사한 결과이다. 그림에서는 사각형 기호가 W 성분이 모체로부터 분리되지 않은 경우, 삼각형 기호가 분리된 경우를 나타내며, 이때 빈 삼각형은 분리 비율 Ω ≤ 0.5, 채워진 삼각형은 Ω > 0.5를 의미한다. 그림의 임계선을 통하여 분리 발생 여부를 예측할 수 있는 경계 조건을 설정할 수 있다. 예를 들어,
D0/
d ≥ 1/6 및
Wew ≥ 50 이상의 조건에서는 대부분 분리가 발생하며, 반대로
D0/
d ≤ 1/2 및
Wew < 30 이하에서는 거의 분리가 관찰되지 않는다. 대체적으로
D0/
d 및
Wew가 모두 증가할수록, 즉 표면곡률이 크고 관성력이 큰 경우, W 성분의 분리 가능성이 뚜렷하게 증가함을 보여준다. 이는 곡률이 클수록 곡면의 원주방향으로의 퍼짐이 약해지고, 원주방향의 수축이 강하게 발생한 결과로 보인다. 이 결과는 액적 분리를 유도하고자 할 때, 표면 곡률과 초기 운동량(충돌 속도)을 어떻게 조절해야 하는지를 구체적으로 제시해준다. 중간 곡률(
d4과
d6) 표면에서는 원주방향으로 큰 부피의 액적 퍼짐이 발생하기 때문에서 큰 곡률(
d2) 표면과 비교하여 분리효율이 높게 예측되었다.
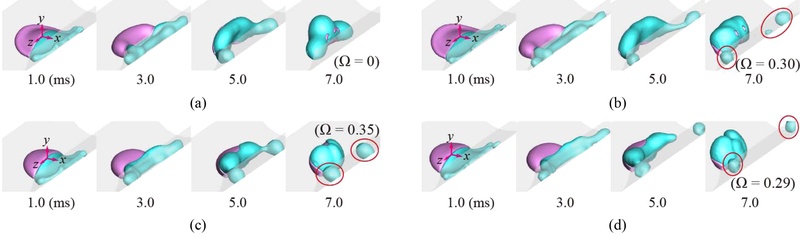
야누스 액적의 성분간 점도비와 초기 관성력이 액적의 충돌 거동에 미치는 영향을 분석하기 위해 동일한 표면 곡률 조건에서 액적의 형태 변화를
Fig. 4에 나타내었다. 이를 통해 점도비(
α) 및
Wew가 액적의 비대칭 동역학에 어떤 영향을 미치는지를 정성적으로 파악할 수 있다. 낮은 점도비(
α1)에서, W와 G 성분 간의 점도 차이가 작아 두 성분이 유사한 퍼짐현상으로 진화되며 비교적 대칭적인 형태 유지하였다(
Fig. 4(a), 1.0 ms). 하지만 W 성분은 곡면의 축 방향으로 강한 퍼짐이 나타났고, 낮은
Wew로 인하여 분리 없이 모체(mother drop)과 함께 수축되었다(Ω = 0). 높은 점도비(
α4)에서, G 성분이 매우 높은 점도를 가지므로 거의 움직이지 않고 고정된 형태를 유지하는 반면, W 성분은 빠르게 퍼지고 길게 늘어나며 비대칭적인 액적 형태를 형성한다(
Fig. 4(b)). 수축 과정에서도 G 부분이 거의 변형되지 않는 반면, W 성분만이 축방향으로 길어지고 분리되는 경향을 보인다(Ω = 0.35). 고점도비에서 W 성분의 수축과정에서 원주방향의 빠른 수축이 저점도비와 비교하여 관찰되었고 이러한 결과는 액적 분리로 이어진 것을 확인하였다.
Fig. 4 Effect of the viscosity ratio and impact velocity on the spreading and retracting behavior. (a) and (b) Dynamic behavior of drops with α = α1 and α4, respectively, under Wew = 44 and d/D0 = 2.0, (c) and (d) Dynamic behavior of drops with α = α1 and α4, respectively, under Wew = 57 and d/D0 = 2.0
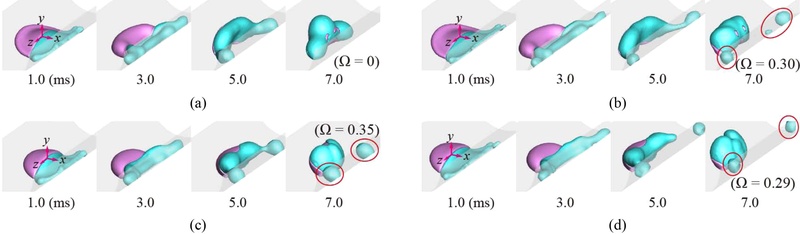
Fig. 4(c)에서 관성력이 증가함에 따라, W 성분이 곡면 축 방향의 더욱 넓은 영역으로 퍼지지만 여전히 G 성분과 함께 일정수준의 대칭 구조를 유지한다. 상기 언급된 낮은
Wew 조건에 비해 퍼짐 및 수축 속도가 전반적으로 증가하였으며, 분리현상이 관찰되었다(Ω = 0.30).
Fig. 4(d)는 고점도비와 높은 관성력을 가진 가장 극적인 비대칭성을 보여준다. G 성분은 여전히 거의 정지 상태를 유지하는 반면, W 성분은 큰 관성력에 의해 곡면을 따라 빠르게 퍼진 후, 중심으로 수축하지 않고 곡면 축방향으로 양 끝으로 강하게 분리되는 경향을 보인다(Ω = 0.29).
Figs. 4(c)와 4(d)를 비교할 때, 분리가 발생하는 시간적인 시점도 고점도비에서 더 빠르다. 이와 같은 현상은 W 성분의 체류시간 감소, 분리 가능성 증가, 그리고 액적 내 운동량 불균형을 유발하는 주요 원인으로 작용할 것으로 보인다.
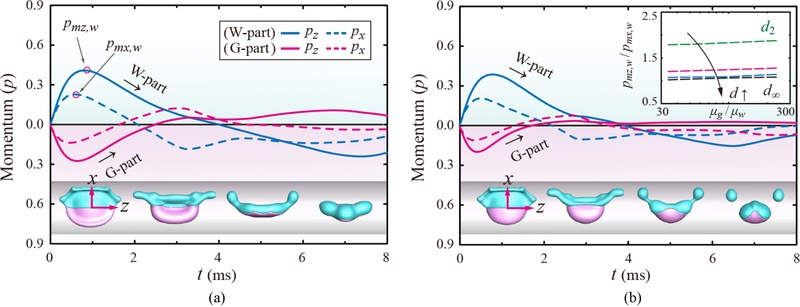
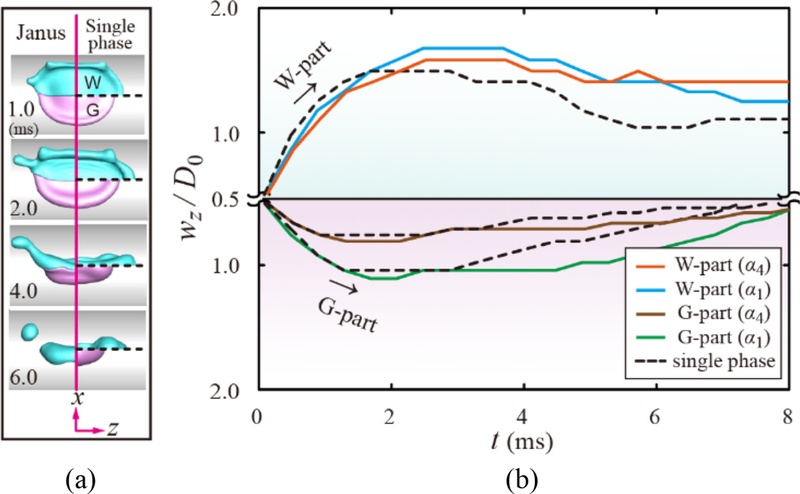
야누스 액적의 비대칭적인 수축 및 분리 현상을 정량적으로 분석하기 위해,
Fig. 5에서는 충돌 이후 시간에 따른
x 및
z 방향의 운동량 변화를 제시하였다. 그림에서 실선은
z 방향 운동량인
pz, 점선은
x 방향 운동량인
px를 나타내며, 각각의 그래프는 상단(W 성분)과 하단(G 성분)으로 나누어 두 유체 성분의 운동 특성을 구분하여 표현하였다. 그림 하단에 배치된 상면(Top-view) 스냅샷은 네 개의 대표적인 시간 지점을 기준으로 액적의 형태 변화를 시각화한 것으로, 운동량 변화와 형태 변화 간의 상관관계를 보여준다. 운동량의 시간에 따른 변화 추적은 W 및 G 성분이 표면 충돌 이후 어떠한 궤적을 따르는지를 이해하는 데 핵심적인 정보를 제공한다. 여기서
px와
pz의 부호는 유체의 운동 방향을 의미하며, 예를 들어
px> 0은 퍼짐(Spreading)을,
px < 0은 수축(Retraction)을 의미한다. 이러한 정량적 분석은 액적의 비대칭적 반동, 변형 및 분리 메커니즘을 이해하는 데 기반이 된다.
Fig. 5 Temporally resolved axial momenta for different viscosity ratios. (a) and (b) Axial momenta (p) in the x and z directions for W (top) and G parts (bottom), obtained at α = α1 and α4, respectively (Wew = 44). Illustrations of the insets of (a) and (b) indicate the top-view snapshots captured at distinct times. The inset of (b) represents the ratio of the maximal momenta between the x and z directions, as a function of the viscosity ratio for several cylinder’s diameters, including d/D0 = 2.0 (green), 4.0 (pink), 6.0 (blue), and infinity (black), under Wew = 44
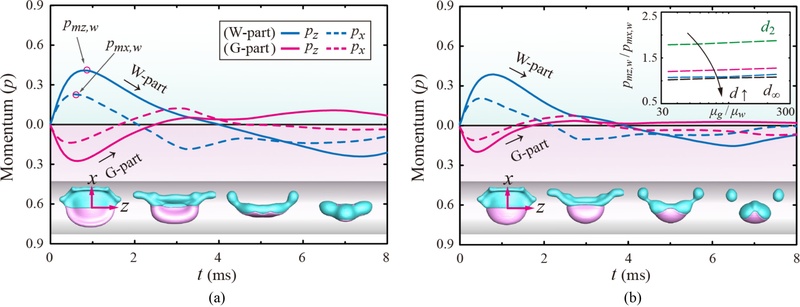
낮은 점도비에서 W 및 G 성분 모두에서 퍼짐 운동량의 변화가 유사한 경향을 보인다(
Fig. 5(a)).
px 운동량은 약 2 ms 이후,
pz 운동량은 약 4 ms 이후, 수축(Retraction) 단계에 들어서면서 감소하고,
px와
pz 모두 음의 값으로 전환된다. 특히 액적 체류시간에 해당되는 약 4 ms 가 될 때까지 W 성분의
pz는 양의 값을 가지고 있었고,
px는 그 시간 동안 부호가 바뀌어 수축단계를 유지하고 있었다. 이 결과는 그림 하단의 액적 형상에서 볼 수 있듯이, W 성분의
z 축으로의 긴 액적 정렬 현상을 유도하였다. 낮은 점도비에서 G 성분은 수축단계에서 큰 운동량 값을 가지고 약 2-4 ms 에서 양 방향으로 수축을 진행하였다.
높은 점도비에서 W 성분의 퍼짐은 낮은 점도비에서 관찰된 것과 거의 유사하다(
Fig. 5(b)). 차이점은 수축 단계(2-4 ms)에서
x 축의 수축 운동량이 상대적으로 약한 것으로 보인다. 또한 액적 분리가 일어나는 약 5 ms 이후에
z 축의 수축 운동량이 상대적으로 약한 것으로 나타났다. 공통점은 낮은 점도비와 유사하게 액적 체류시간에 해당되는 약 4 ms 가 될 때까지 W 성분의
pz는 양의 값을 가지고 있었고,
px는 그 시간 동안 부호가 바뀌어 수축단계를 유지하고 있는 것이다. G 성분은 높은 점도에 의해 초기에 나타나는 운동량도 작고, 빠르게 0에 수렴하면서 실질적인 퍼짐 거동을 보이지 않는다. G 성분은 표면에 고정되거나 매우 천천히 반응하며 거의 정지된 상태로 유지된다. 그럼에도 불구하고 고점도비의 G 성분은
z 축 방향의 퍼짐을 억제하여 W 성분의 탈착을 유도하는 역할을 하였기 때문에 두 점도비에서의 분리/비분리 결과가 달라졌다.
Fig. 5(b)의 삽입 그림에서는 축 간의 최대운동량 비(
pmz/
pmx)를 서로 다른 곡률조건 및 점도비에 따라 조사하였다. 곡률이 클수록 (즉,
d/
D0가 작을수록) 같은
α 조건에서
pmz/
pmx이 더 크며, 이는 곡면의 곡률은 두 축의 운동량비에 큰 영향을 미친다는 것을 알 수 있었다. 또한 점도비가 증가함에 따라 운동량비는 증가하지만 곡률 인자와 비교하여 그 영향력은 크지 않은 것으로 나타났다.
축 방향으로의 액적 정렬 거동을 분석하기 위해,
Fig. 6(a)에서는 야누스 액적과 단상 액적의 시간에 따른 형태 변화를 비교하였다. 좌측에는 야누스 액적의 동적 변화가, 우측에는 동일 조건에서의 단상 액적(즉, W 성분과 G 성분을 각각 독립된 단상 유체로 구성한 경우)의 변화를 병렬적으로 제시하였다. 정량적 분석을 위하여
Fig. 6(b)에서
z 방향의 길이 변화를 표현하였다. 단상 액적에 비해 야누스 액적 내 W 성분은 2 ms 이후부터
z 방향으로의 길이 증가가 뚜렷하게 나타났다. 이는 수축 과정 중 G 성분의 존재로 인하여
z 방향으로 길이가 증가하는 효과가 생겼다. 야누스 액적의 G 성분은 이와 유사하게 2 ms 이후부터
z 방향으로의 길이가 단상 액적과 비교하여 더 길었다. 6 ms 에서의 액적 형상을 비교하였을 때, 야누스 액적은 분리되었고, 단상 액적은 수축 단계에서
z 방향 길이가 감소하고 있는 것을 알 수 있다. 이 결과는 야누스 액적은 점도 조합 및 곡면 설계를 통한 분리 메커니즘을 제어할 수 있는 기반을 제공할 수 있다는 것을 보여주었다.
Fig. 6 Comparison of the temporal evolution of the spreading drop into liquid elongation on z direction. (a) Top-view snapshots of Janus (left) and single-phase water (right and top) and single-phase mixture (right and bottom) over time at α = α1 and (b) Temporal variation of the z-length from the impact point for water (up) and mixture (down) under Wew = 50 and d/D0 = 2.0
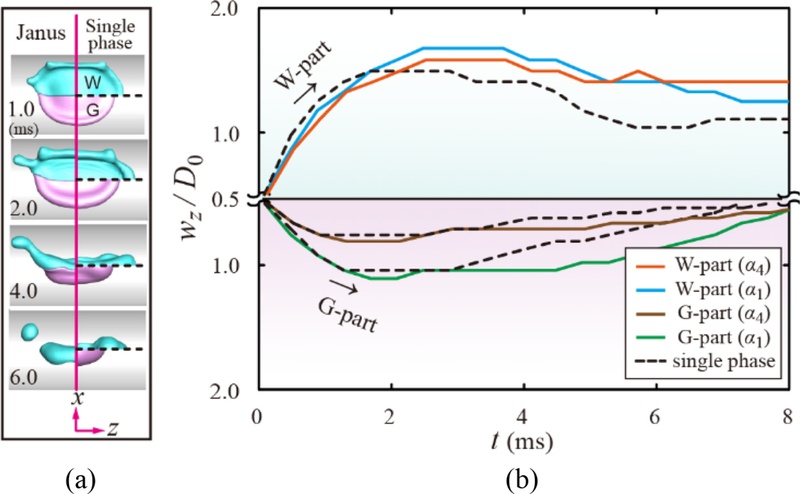
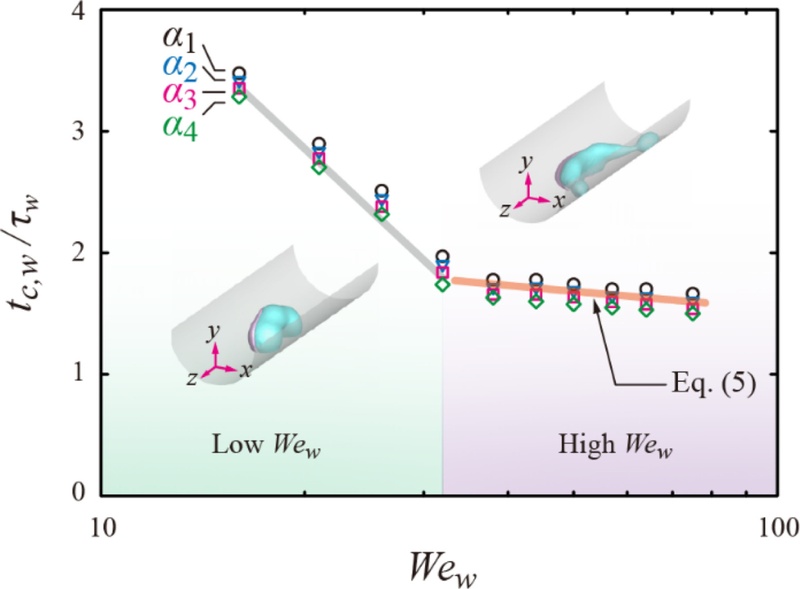
Fig. 7은 동일한 곡률 조건에서 다양한 점도비(
α)에 대해 W 성분의 체류시간이 Weber 수에 따라 어떻게 변화하는지를 나타낸 것이다. 대체적으로 모든 점도비 조건에서 Weber 수 증가에 따라 W 성분의 체류시간은 감소하는 경향을 보인다. 이는 충돌 속도가 증가할수록 액적의 관성력이 커지고, 이에 따라 액적 비대칭 형상 변화가 더 유도되기 때문이다. 이 그림에서 체류시간이 크게 감소하는 영역인 낮은
Wew 영역과 작게 감소하는 영역인 높은
Wew 영역으로 구분하였다. 낮은
Wew 영역에서는, W 성분이 퍼진 후 비교적 천천히 수축되며, G 성분과의 접합부를 유지한 채 중심부로 회복된다. 이때 체류시간은 길게 유지되며, 반동 없이 표면 상에 잔류하거나 재결합하는 현상이 지배적이다. 삽입 그림에서 볼 수 있듯이 액적의 W 및 G 성분의 큰 비대칭성을 관찰하기 어렵다. 높은
Wew 영역에서는, 충돌 직후 빠른 퍼짐이 발생하고, 이어서 퍼짐 단계에서 축 방향의 액적 정렬 현상이, 수축 단계에서 원주방향의 큰 수축 현상이 일어나고 결국 분리가 되는 현상이 관찰된다. 이 경우 체류시간은 급격히 짧아지며, 액적의 비대칭 운동에 의한 동적 분리가 주요 특성으로 나타난다.
Fig. 7 Water part’s residence time as a function of Wew for different viscosity ratios at d/D0 = 2.0. Illustrations of the insets indicate the characteristics of retracting shown with snapshots for two Wew regimes
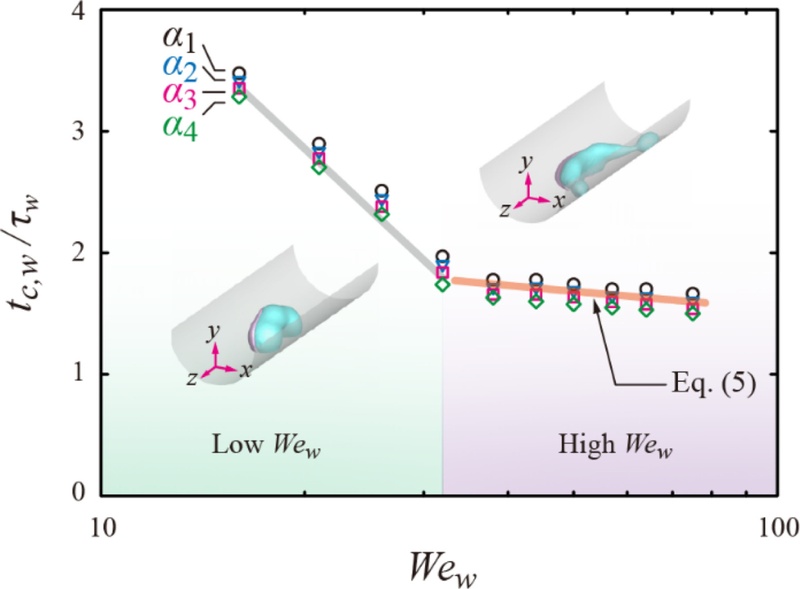
높은
Wew 영역에서 체류시간의 감소에 대하여 관계식을 예측하였다. W 성분의 체류시간은
x 및
z 방향의 최대 퍼짐 직경(
Dmx 및
Dmz)과 충돌속도(
V0)로 표현할 수 있다. 부피 보존 조건으로부터
D03∼DmzDmxh를 만족한다. 액막 두께는 관성–표면장력 지배 현상으로 인한 관계식
h∼D0Wew-1/2 [
22]으로 주어진다.
x 방향의 수축속도를
ux (~
Dmx/
tc,
w)로 가정하고,
z 방향의 퍼짐 시간은
Dmz/
V0에 비례하고 최대 퍼짐 시 액적은 표면에서 이탈한다고 가정할 때,
식(4)와 같은 관계식을 갖는다.
단상 액적이 볼록한 표면에 충돌하는 경우, 곡면에 의한 코안다(Coandă) 효과에 의하여 수축속도가 제시되었다[
10]. 본 연구에서는 볼록한 표면과 달리 오목한 표면 위 코안다 효과는 매우 약하게 작용하므로, 액막 내 곡률로 인한 법선방향 압력 구배
∂P/∂n∼ΔP/h∼∂ρV02/d를 적용하였고, 운동량 방정식
ρux∂ux/∂lx=-∂P/∂lx을 통하여 원주방향의 수축속도를 다음과 같이 제시하였다:
ρux2/lx∼ΔP/lx∼ρV02h/lxd. 이를 정리하면
ux/V0∼h/ d1/2로 나타낼 수 있으므로 최종적으로 스케일링 해석을
식(5)와 같이 제시할 수 있었다.
야누스 액적의 점도비 효과를 고려할 때,
α1≤α≤
α4, 44≤
Wew≤75, and 2.0≤
d/
D0≤8.0 조건에서,
f(α)∼α-1/20의 관계를 본 수치해석 데이터를 가지고 대입하였다.
Fig. 7의 높은
Wew 영역에서 나타난 데이터를 위 식과 비교한 결과, 체류시간 감소 경향이 수치해석 결과와 일치하는 양상을 보이는 것을 확인할 수 있었다. 그럼에도 불구하고, 점도비에 따른 이론적인 체류시간 스케일링과 낮은
Wew 영역에서의 체류시간 감소 등은 설명이 필요하며, 이론적 해석은 추후 제안될 과제로 보인다.
본 연구를 통하여 야누스 액적 내에서의 점도비와 표면 곡률 변화는 W 및 G 성분의 유동 비대칭성과 체류시간 변화에 영향을 주는 인자로 확인하였다.
4. 결론
본 연구에서는 곡면 위에서의 야누스 액적 충돌 현상에 대한 동적 거동 및 체류시간을 VOF 수치해석 방법을 이용하여 예측하였다. 야누스 액적의 충돌 거동에 있어 점도비 및 표면 곡률이 액적의 비대칭 유동, 체류 시간, 그리고 분리 현상에 미치는 영향을 수치적으로 규명하였다. 곡률이 증가할수록 축 방향 퍼짐과 원주방향 수축이 지배적으로 커지면서 W 성분의 분리 가능성이 뚜렷하게 증가하였다. 또한, 높은 점도비와 높은 Wew 조건에서는 G 성분이 중심에 거의 고정된 상태로 W 성분의 강한 비대칭 퍼짐 및 분리를 유도함을 확인하였다. 체류 시간은 Wew 가 증가함에 따라 급격히 감소하며, 이때 나타나는 스케일링 관계를 제안하였고 수치 데이터와 정성적으로 일치하였다. 결과적으로, 본 연구는 점도 조합 및 표면 곡률 설계를 통해 야누스 액적의 분리 및 유동 방향성을 정밀하게 제어할 수 있는 물리적 기반을 제공하며, 이는 선택적 액체 분리, 표면 기능화, 미세유체설계 등 다양한 응용 분야에 활용될 수 있을 것을 보인다.
ACKNOWLEDGMENTS
This was supported by Korea National University of Transportation in 2025.
REFERENCES
- 1.
Breitenbach, J., Roisman, I. V., Tropea, C., (2018), From drop impact physics to spray cooling models: A critical review, Experiments in Fluids, 59, 1-21.
10.1007/s00348-018-2514-3
- 2.
Quéré, D., Reyssat, M., (2008), Non-adhesive lotus and other hydrophobic materials, Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences, 366(1870), 1539-1556.
10.1098/rsta.2007.2171
- 3.
Damak, M., de Ruiter, J., Panat, S., Varanasi, K. K., (2022), Dynamics of an impacting emulsion droplet, Science Advances, 8(11), eabl7160.
10.1126/sciadv.abl7160
- 4.
Lohse, D., (2022), Fundamental fluid dynamics challenges in inkjet printing, Annual Review of Fluid Mechanics, 54(1), 349-382.
10.1146/annurev-fluid-022321-114001
- 5.
Sefiane, K., Duursma, G., Arif, A., (2021), Patterns from dried drops as a characterisation and healthcare diagnosis technique, potential and challenges: A review, Advances in Colloid and Interface Science, 298, 102546.
10.1016/j.cis.2021.102546
- 6.
Wei, Y., Thoraval, M.-J., (2021), Maximum spreading of an impacting air-in-liquid compound drop, Physics of Fluids, 33(6), 061703.
10.1063/5.0053384
- 7.
Blanken, N., Saleem, M. S., Thoraval, M.-J., Antonini, C., (2021), Impact of compound drops: A perspective, Current Opinion in Colloid & Interface Science, 51, 101389.
10.1016/j.cocis.2020.09.002
- 8.
Yu, F., Lin, S., Yang, J., Fan, Y., Wang, D., Chen, L., Deng, X., (2020), Prompting splash impact on superamphiphobic surfaces by imposing a viscous part, Advanced Science, 7(4), 1902687.
10.1002/advs.201902687
- 9.
Yun, S., Kim, J., Kim, G. H., (2022), Dynamic characteristics of ellipsoidal Janus drop impact on a solid surface, Physics of Fluids, 34(10), 102104.
10.1063/5.0118969
- 10.
Hwang, D., Yun, S., (2023), Bouncing characteristics of Janus drop impact on curved surfaces, Physics of Fluids, 35(6), 062015.
10.1063/5.0159002
- 11.
Zhang, B., Sanjay, V., Shi, S., Zhao, Y., Lv, C., Feng, X. Q., Lohse, D., (2022), Impact forces of water drops falling on superhydrophobic surfaces, Physical Review Letters, 129(10), 104501.
10.1103/PhysRevLett.129.104501
- 12.
Han, J., Kim, W., Bae, C., Lee, D., Shin, S., Nam, Y., Lee, C., (2020), Contact time on curved superhydrophobic surfaces, Physical Review E, 101(4), 043108.
10.1103/PhysRevE.101.043108
- 13.
Liu, Y., Andrew, M., Li, J., Yeomans, J. M., Wang, Z., (2015), Symmetry breaking in drop bouncing on curved surfaces, Nature Communications, 6(1), 1-8.
10.1038/ncomms10034
- 14.
Regulagadda, K., Bakshi, S., Das, S. K., (2018), Triggering of flow asymmetry by anisotropic deflection of lamella during the impact of a drop onto superhydrophobic surfaces, Physics of Fluids, 30(7), 072105.
10.1063/1.5041824
- 15.
Zhang, H., Jin, Z., Jiao, M., Yang, Z., (2018), Experimental investigation of the impact and freezing processes of a water droplet on different cold concave surfaces, International Journal of Thermal Sciences, 132, 498-508.
10.1016/j.ijthermalsci.2018.06.032
- 16.
Rajesh, R. S., Naveen, P. T., Krishnakumar, K., Ranjith, S. K., (2019), Dynamics of single droplet impact on cylindricallycurved superheated surfaces, Experimental Thermal and Fluid Science, 101, 251-262.
10.1016/j.expthermflusci.2018.10.011
- 17.
Jowkar, S., Morad, M. R., (2019), Rebounding suppression of droplet impact on hot surfaces: effect of surface temperature and concaveness, Soft Matter, 15(5), 1017-1026.
10.1039/C8SM02271B
- 18.
Hirt, C. W., Nichols, B. D., (1981), Volume of fluid (VOF) method for the dynamics of free boundaries, Journal of Computational Physics, 39(1), 201-225.
10.1016/0021-9991(81)90145-5
- 19.
Rider, W. J., Kothe, D. B., (1998), Reconstructing volume tracking, Journal of Computational Physics, 141(2), 112-152.
10.1006/jcph.1998.5906
- 20.
Brackbill, J. U., Kothe, D. B., Zemach, C., (1992), A continuum method for modeling surface tension, Journal of Computational Physics, 100(2), 335-354.
10.1016/0021-9991(92)90240-Y
- 21.
Leonard, B. P., (1979), A stable and accurate convective modelling procedure based on quadratic upstream interpolation, Computer Methods in Applied Mechanics and Engineering, 19(1), 59-98.
10.1016/0045-7825(79)90034-3
- 22.
Clanet, C., Béguin, C., Richard, D., Quéré, D., (2004), Maximal deformation of an impacting drop, Journal of Fluid Mechanics, 517, 199-208.
10.1017/S0022112004000904
Biography
- Sungchan Yun
Professor in the Department of Mechanical Engineering, Korea National University of Transportation. His research interest is micro/nano phenomena.