ABSTRACT
This study details the development of a semi-active suspension wheel module for small mobile robots and assesses its dynamic characteristics under various driving conditions through simulation. The wheel module features a low-degree-of-freedom mechanical design and includes a semi-active damper to improve adaptability to different environments. To validate the simulation model, a prototype robot equipped with the wheel module was created, and obstacle-crossing experiments were conducted to measure vertical acceleration responses. The model was then refined based on these experimental results. By employing design of experiments and optimization techniques, the effective range of damping coefficients was estimated. Additionally, simulations were carried out at different speeds, payloads, and obstacle heights to identify optimal damping values and examine their trends. The results indicate that the proposed module significantly enhances driving stability and can serve as a foundation for future control strategies in robotic mobility systems.
-
KEYWORDS: Wheel module, Semi-active suspension, Dynamic analysis, Damping coefficient, Small mobile robot, Driving performance
-
KEYWORDS: 휠 모듈, 반능동 서스펜션, 동역학 해석, 감쇠 계수, 소형 이동 로봇, 주행 성능
1. 서론
소형 이동 로봇(Small Mobile Robot)은 물류, 서비스, 재난 대응, 우주, 군사, 스마트 농업 등과 같이 다양한 분야에서 활용되고 있으며
[1-
3], 이로 인해 실내외 여러 지형을 안정적으로 주행하기 위한 기술적인 요구 또한 커지고 있다. 소형 이동 로봇은 크기, 무게, 전력 공급 측면에서 제약이 큰 구성 요소를 효율적으로 통합하는 설계가 필수적이다.
최근 이러한 이동 플랫폼의 제약들을 극복하기 위한 방안으로 휠 모듈(Wheel Module)이 제시되고 있다
[4,
5]. 휠 모듈은 구동(Driving), 제동(Breaking), 조향(Steering), 서스펜션(Suspension) 기능을 하나의 유닛으로 통합한 구조로, 개별적인 제어와 최적화가 가능하며 고장 시 유지보수나 교체가 용이하다는 장점이 있다. 특히, 다양한 주행 환경에 맞게 설계해야 하는 이동 로봇에 휠 모듈을 활용한 설계는 범용성을 확보할 수 있다.
Fraunhofer IPA에서는 실내 환경을 위한 2륜 차동형 Compact Omnidirectional Wheel Module을 개발하여, 조향 모터를 내부에 통합함으로써 전 방향 주행 구조를 구현하였다
[6]. 농업 분야에서는 Thorvald II와 MARS (Modular Agricultural Robotic System)와 같이 서스펜션, 구동, 조향 기능이 각각 모듈화된 휠 시스템이 제안되었으며, 운용 환경에 따라 모듈을 조합하여 활용하도록 하였다
[7,
8]. 또한, Georgia Tech에서는 Degenerate Wheel 구조를 활용하여 측면 공간 활용도를 높인 SDM (Synchron ous Driving Module) 개발을 통해 주행 방향의 제약을 최소화하는 휠 모듈 시스템을 제시하였다
[9]. 이러한 휠 모듈의 선행 연구들은 대부분 특정 목적 및 운용 환경에 최적화되어 있으며, 구동 메커니즘과 기계적 통합에 중점을 두고 있다. 이에 따라, 충격 및 진동 흡수를 위한 서스펜션 기능은 생략되거나 수동 방식 사용에 국한되는 경우가 많다. 진동 저감 기능이 적용된 일부 사례 또한 주로 대형 플랫폼을 대상으로 하고 있어, 소형 이동 로봇에 적합한 서스펜션 통합 연구는 아직 부족한 실정이다.
서스펜션 시스템은 크게 수동(Passive), 반능동(Semi-active), 능동(Active) 방식으로 분류되며, 이 중 반능동 방식은 구조가 비교적 단순하고 전력 소모가 적으면서 감쇠력을 조절할 수 있어 외란에 대응할 수 있다는 장점이 있다
[10,
11]. 이러한 특성은 공간, 중량, 전력 자원 등의 제약을 받는 소형 이동 로봇 플랫폼에 특히 적합하며, 다양한 주행 조건에서도 진동과 충격을 효과적으로 완화하여 주행 안정성을 확보할 수 있다. 따라서, 반능동 서스펜션 기반 휠 모듈은 소형 로봇의 기동성과 운용 효율성을 동시에 향상시킬 수 있는 현실적이고 실용적인 해법으로 주목된다.
이러한 휠 모듈의 실효성을 확보하기 위해서는 다양한 주행 조건에서의 감쇠 계수 변화에 따른 로봇 주행 성능에 미치는 영향을 분석해 볼 필요가 있다. 감쇠 계수는 외란 응답 특성을 좌우하는 제어 변수로, 시스템의 동특성을 형성하는 데 중요한 역할을 한다. 특히, 주행 속도나 하중, 장애물 높이 등 운용 조건이 달라질 때, 감쇠 계수를 적절히 조절하여 주행 성능을 효과적으로 유지하거나 향상시킬 수 있다
[12,
13].
이에 본 연구에서는 반능동 서스펜션을 탑재한 소형 이동 로봇용 휠 모듈을 제안하고, 이를 적용한 실험용 플랫폼을 기반으로 시뮬레이션 모델을 개발하고, 실제 실험을 진행하였다. 실험 데이터를 바탕으로 순차적 근사 최적화 기법을 통해 해석 모델을 정교화하고, 감쇠 계수 변화에 따른 로봇 주행 응답 및 성능을 수치적으로 비교함으로써 시뮬레이션 모델의 신뢰성을 확보하였다. 이후 다양한 주행 조건을 설정하여 감쇠 계수 변화에 따른 로봇의 진동 응답을 분석하고, 주행 안정성을 확보할 수 있는 최적 감쇠 계수의 경향성을 체계적으로 도출하였다.
본 논문의 구성은 다음과 같다. 2장에서는 반능동 서스펜션이 탑재된 소형 이동 로봇용 휠 모듈을 제안하고, 기구학적 및 동역학적 해석을 통해 시스템 사양을 도출한다.
3장에서는 휠 모듈이 장착된 실제 로봇 플랫폼을 기반으로 동역학 해석 모델을 구성하고, 실험을 통해 반능동 서스펜션의 감쇠 계수 범위를 추정하여 해석 모델의 신뢰성을 확보한다. 4장에서는 향상된 해석 모델을 통해 주행 속도, 로봇의 하중, 장애물 높이 등 다양한 운용 조건을 고려한 시뮬레이션을 수행하여, 감쇠 계수 변화에 따른 주행 성능을 분석한다. 또한, 최적 감쇠 계수의 경향성을 도출함으로써 휠 모듈의 범용적 활용을 위한 기초 데이터를 제시한다.
2. 반능동 서스펜션 휠 모듈 설계
2.1 휠 모듈 메커니즘의 구성
본 연구에서 제안하는 휠 모듈은 반능동 서스펜션이 적용된 구조로,
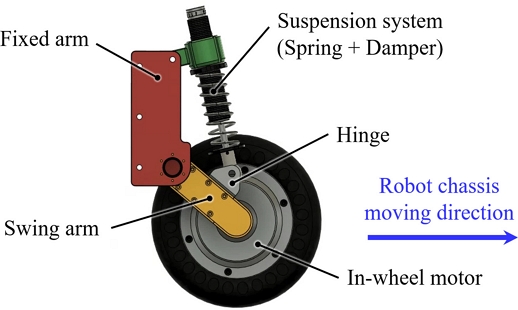
Fig. 1과 같이 인휠모터(In-wheel Motor), 고정암(Fixed Arm), 스윙암(Swing Arm), 그리고 스프링(Spring)과 댐퍼(Damper)로 이루어진 서스펜션 시스템(Suspension System)으로 구성된다.
Fig. 1Wheel module mechanism
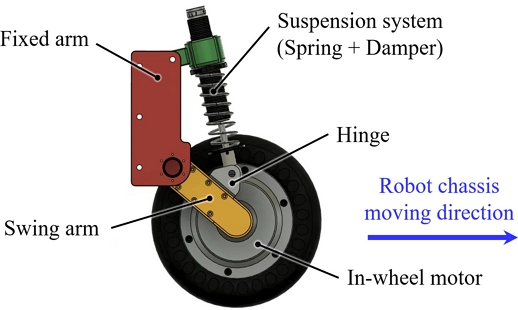
고정암은 로봇 본체에 고정되며, 스윙암은 고정암과 수동 회전 조인트(Joint)로 연결되어 있어 회전 조인트 축을 중심으로 상하로 움직일 수 있다. 고정암과 스윙암 사이에 위치한 서스펜션 시스템은 주행 시 발생하는 충격 작용 방향에 따라 기울어지게 배치하여 지면 충격과 로봇 본체 하중에 따른 힘을 효과적으로 흡수하고 진동을 최소화할 수 있도록 하였다. 이러한 휠 모듈의 배치는 휠 모듈 시스템의 공간을 확보함과 동시에, 스트로크(Stroke)를 길게 유지하여 큰 힘을 흡수할 수 있다
[14].
휠 모듈은 하나의 평면 상에 배치된 단순한 구조로 설계되었으며, 제어 요소를 최소화한 저자유도 설계를 통해 무게와 부피를 줄였다. 이러한 구조는 다양한 이동 로봇 플랫폼에 쉽게 적용할 수 있도록 모듈화의 기반을 제공할 수 있으며, 해석 모델 구축부터 실제 제작까지 높은 효율성을 가진다.
2.2 휠 모듈 서스펜션 시스템의 사양 도출
휠 모듈에 적용된 서스펜션 시스템은 로봇 주행 시 지면으로부터 전달되는 진동 및 충격과 같은 외란을 효과적으로 흡수하여 주행 안정성을 확보할 수 있어야 한다. 소형 이동 로봇의 구조적 제약 내에서 서스펜션 탑재 공간을 확보하고, 여러 하중 조건에서도 충분한 스트로크와 감쇠 성능을 보일 수 있도록 기구학 및 동역학 분석을 기반으로 사양을 도출하였다.
2.2.1 기구학적 분석
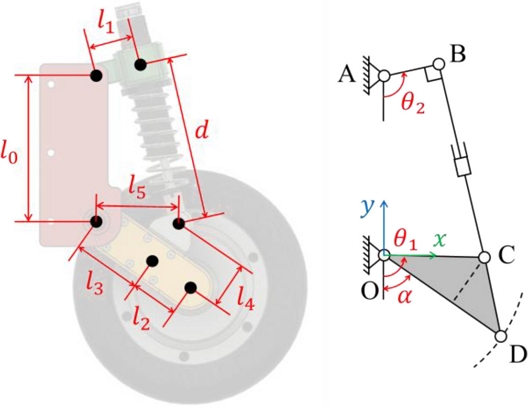
서스펜션 시스템 사양 선정을 위해 스트로크 한계를 도출하고자 기구학적 분석을 수행하였다. 고정암과 스윙암 사이 회전 조인트 위치를 좌표계의 원점
O로 설정하였으며, 링크 길이 및 링크 간 각도를 기구학적 파라미터로 정의하였다. 이는
Fig. 2에 기구 해석도와 함께 나타내었다.
Fig. 2Parameters and kinematic diagram of the wheel module
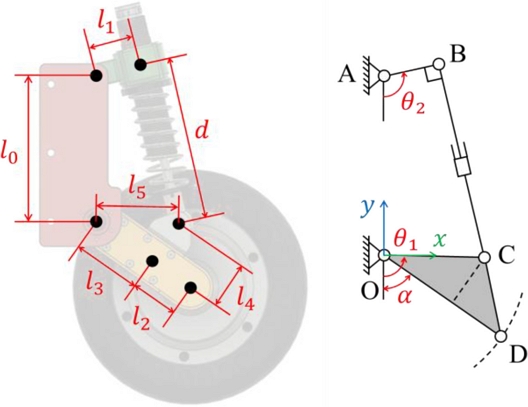
휠 모듈은 닫힌 연쇄 구조(Closed-chain Mechanism)를 기반으로 동작하며, 전체 구조의 형상 유지 조건을 고려하여 회전 조인트 각도
θ1의 범위를 설계된 CAD 모델을 통해 사전 검토하였다. 이때, 유효 각도 범위는 33.69˚에서 132.68˚로 제한된다. 서스펜션 스트로크
d는 조인트 각도
θ1의 함수로 나타낼 수 있으며, 이는
식(1) 및
식(2)와 같이 표현된다.
이를 통해, 앞서 제한한 조인트 각도 θ1 범위에 따른 서스펜션 스트로크 d는 86.4에서 188 mm 사이임을 확인할 수 있다. 최종적으로 실제 조립 시 발생하는 간섭까지 고려했을 때, 유효한 스트로크는 최소 42.4에서 최대 144 mm로 산출 가능하다.
2.2.2 동역학적 분석
로봇의 하중 및 주행 중 발생할 수 있는 충격량을 고려하여, 서스펜션에 작용하는 정격 하중을 검토하기 위해 휠 모듈에 대한 동역학 해석을 수행하였다.
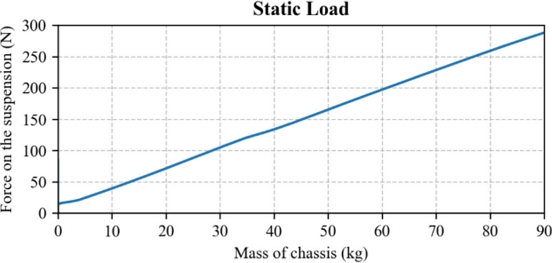
휠 모듈에 하중을 단계적으로 변화시켜 인가하였고, 이에 따른 서스펜션 시스템 압축 변위와 정격 하중을 확인하였다. 그 결과, 서스펜션은 기구학적으로 허용된 범위 내에서 최대 90 kg 하중 조건까지 안정적으로 압축 변위를 수용하는 것으로 나타났다. 이때
Fig. 3에 나타난 바와 같이, 휠 모듈 하나당 약 290 N의 하중이 작용할 수 있음을 확인하였다.
Fig. 3Static load acting on the suspension by mass

2.2.3 서스펜션의 사양 선정
2.1절에서 기술한 바와 같이, 휠 모듈의 서스펜션 시스템은 스프링과 댐퍼로 구성된다. 이러한 서스펜션 구성 요소의 사양은 기구학 및 동역학 분석 결과를 기반으로 설정하였다
[13].
댐퍼의 사양은 로봇의 하중, 에너지 및 충돌 속도 등을 고려하여 선정해야 한다. 이를 위해 실험용 이동 로봇을 기준으로 시간당 충돌 횟수
C, 서스펜션 개수
N, 회전 중심과 서스펜션 간 거리
H, 그리고 전체 하중
W를 변수로 설정하였다.
식(3) 및
식(4)를 통해 운동 에너지 E
K와 일 에너지 E
W를 산출하였으며, 이 두 값을 합산하여 총 에너지 E
T를 계산하였다.
식(6)을 통해 시간당 총 에너지 E
TC를 구하였고,
Table 1과 같은 사양을 갖는 댐퍼 모델을 선정하였다. 해당 모델은 12단계로 감쇠력을 조절할 수 있는 반능동 댐퍼이다.
Table 1Specification of damper
Table 1
|
Parameter |
Value |
|
Stroke [mm] |
40 |
|
Effective weight [kg] |
20-2,150 |
스프링은 작용 하중 및 충격력, 댐퍼 스트로크 S
t를 고려하여 선정하였다. 앞서 도출한 서스펜션 시스템에 가해지는 하중과 허용 스트로크의 범위를 바탕으로 스프링의 밀착 높이
Ls를 산정하였으며, 스프링 설계 기준 JIS B 2704에서 제시하는 바와 같이 허용 하중
P2에서의 길이
L2는 밀착 높이의 1.1배 이상이 되도록 설정하였다. 이는 스프링이 완전히 밀착될 경우 발생할 수 있는 권선 간 간섭과 과도 응력, 그리고 그로 인한 피로 수명 저하를 방지하기 위함이다. 이후 서스펜션에 가해지는 최대 충격력과 정적 하중
P1을 고려하여
식(7)을 통해 스프링 상수
k를 계산하였다.
이러한 계산 결과를 바탕으로, 서스펜션 시스템의 코일 스프링 사양을
Table 2와 같이 선정하였다.
Table 2Specification of coil springs
Table 2
|
Parameter |
Symbol |
Value |
|
Inner diameter [mm] |
D
1
|
3.2 |
|
Outer diameter [mm] |
D
2
|
35.2 |
|
Spring constant [N/mm] |
k
|
5.923 |
|
Free length [mm] |
lF
|
88.5 |
|
Total coil [Coils] |
Nt
|
6 |
|
Active coils [Coils] |
Ne
|
5.5 |
3. 휠 모듈의 해석 모델 개발
3.1 실험용 소형 이동 로봇의 구성
주행 환경에 따라 안정적인 주행이 가능하도록 하는 휠 모듈의 최적 감쇠 계수를 확인 및 분석하기 위해, 최적화된 시뮬레이션 모델을 개발하고자 하였다. 이를 위해서는 실제 실험 결과를 기반으로 한 해석 모델의 최적화 과정이 선행되어야 한다. 이에 따라,
Fig. 4(a)와 같이 휠 모듈이 장착된 소형 이동 로봇을 제작하였다.
Fig. 4Configuration of the small mobile robot system with wheel module
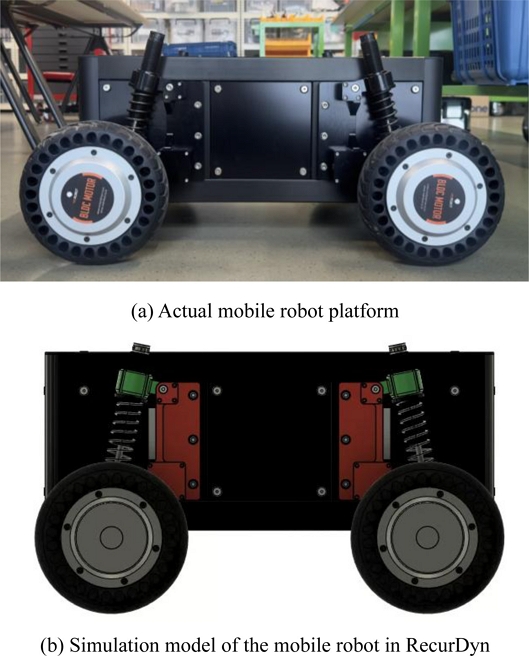
로봇은 직육면체 형상의 본체에 4개의 휠 모듈이 부착되어 있는 형태이며, 사륜 구동 방식이다. 조향의 경우 별도의 장치가 필요하지 않은 미끄럼 조향(Skid steering) 방식을 채택하였으며, 이를 통해 구조적인 복잡함을 줄이면서 기동성을 확보할 수 있도록 하였다.
앞서 2.1절에서 언급한 바와 같이, 휠 모듈의 경우 주행 중 발생하는 충격 작용 방향에 따라 기울어지게 배치하였다. 실제 로봇 시스템에서는 전후 서스펜션의 기울기가 서로 반대 방향으로 장착되어 있으며, 이는 동일 방향으로 배치할 경우에 설계 특성상 발생할 수 있는 휠베이스(Wheel-base) 축소와 하중 분산의 불리함을 해소하여 주행 안정성을 확보하기 위함이다.
제작된 플랫폼의 총 중량은 약 60.64 kg이며, 실험 환경에서 주행 충격과 진동 반응 데이터를 수집할 수 있도록 고정암 부분에 IMU (Inertial Measurement Unit) 센서를 부착하였다.
3.2 해석 모델 개발
해석 모델은 상용 다물체 동역학 해석 소프트웨어인 RecurDyn을 활용하여
Fig. 4(b)와 같이 모델링하였으며, 설계된 3D CAD 데이터를 기반으로 실제 로봇 형상 및 구성을 반영하였다.
해석 정확도를 높이기 위해 각 구성 요소의 질량 정보는 실제 측정값을 반영하였으며, 모델 파라미터는 설계 단계에서 도출된 값을 적용하였다. 스프링 상수 k는 5.923 N/mm로 설정하였으며, 감쇠 계수 c는 본 연구의 주요 변수이므로 해석마다 변화시킬 수 있도록 하였다. 또한, 휠 모듈의 해석 모델에는 실제와 동일한 위치에 가상의 IMU 센서를 설정함으로써 실제 실험과 같은 조건에서 수직 가속도 및 자세 응답을 모사할 수 있도록 하였다.
3.3 실험에 기반한 해석 모델의 검증
실제와 유사한 해석 모델을 확보하기 위해서 실험과 시뮬레이션 간 비교를 수행하였다.
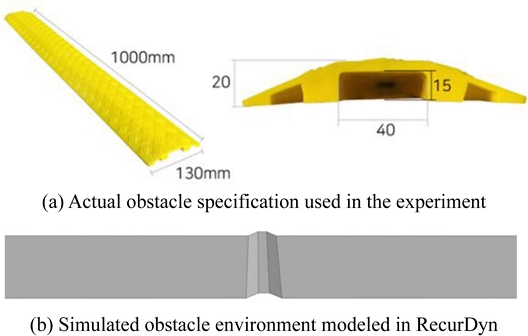
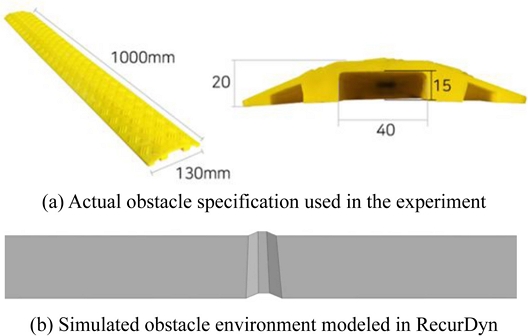
Fig. 5(a)와 같이 실제에서는 상용 전선 보호대를 장애물로 설정하고, 이를 주행하는 조건에서 실험을 수행하였다. 동일한 조건을 구현하고자 해석에서는 해당 규격을 참고하여
Fig. 5(b)와 같이 주행 환경을 모델링하였다.
Fig. 5Environment configuration for experiment and simulation
해석 모델 검증을 위한 응답 변수이자 주요 지표는 수직 가속도의 RMS (Root Mean Square)로 선정하였다. RMS는 진동 신호의 평균 에너지 크기를 나타내는 지표로, 전체 진동 응답의 크기를 안정적으로 평가할 수 있어 로봇 시스템 주행 성능의 판단 기준으로써 적합하다
[15]. 따라서, 반능동 서스펜션의 감쇠 계수를 입력 변수로 설정하였으며, 시뮬레이션 및 실험에서 동일한 위치에 IMU 센서를 부착하여 수집한 응답을 비교하였다.
로봇 시스템의 주행 속도는 사다리꼴 형태의 속도 프로파일을 적용하였으며, 최고 속도 vmax는 0.5 m/s 와 1.0 m/s 두 조건으로 설정하였다. 설정한 속도는 실제로 적용할 수 있는 로봇의 기동 조건을 기반으로 설정된 값이다. 속도 조건에 대해 각각 3회씩 반복 실험을 수행하였다. 속도 프로파일은 가속 및 등속 구간을 포함하며, 총 주행 시간은 30초, 데이터 수집 주기는 100 Hz로 설정하여 실험을 진행하였다.
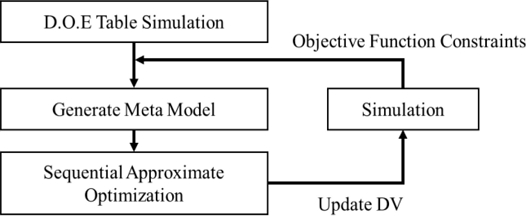
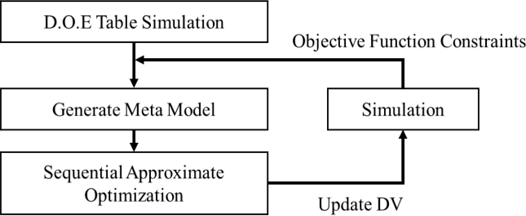
3.3.1 순차적 근사 최적화
본 논문에서는 반능동 서스펜션의 감쇠 계수 범위를 추정하고자 순차적 근사 최적화(Sequential Approximate Optimization, SAO) 기법을 활용하였다
[16,
17].
이는 목적 함수의 반복 평가를 기반으로 근사 모델(Meta Model)을 점진적으로 개선하면서 최적 설계점을 도출해내는 기법으로,
Fig. 6과 같은 순차로 수행된다. 이를 활용하면 복잡한 다물체 동역학 시스템에서 연산 비용을 효율적으로 줄일 수 있다. 특히, 연속적인 입력 변수에 대한 최적화 문제에 적합하며, 비교적 적은 시뮬레이션 반복만으로 높은 수렴도를 기대할 수 있다.
Fig. 6Optimization process in auto design tool of RecurDyn
3.3.2 감쇠 계수 추정 및 해석 모델 검증
앞서 설정한 실험 계획에 따라 실제 실험 및 해석을 진행하였으며, 결과를 토대로 SAO 기법을 적용하였다. 최적화 과정에서는 동역학 해석 프로그램 RecurDyn의 실험계획법(Design of Experiments, DOE) 툴과 최적 설계 알고리즘 툴인 Auto Design을 활용하였다.
SAO 기법 진행을 위해 입력 변수는 댐퍼의 감쇠 계수
c로 설정하였고, 목적 함수
az는 IMU 센서에서 얻은 수직 가속도의 RMS 값으로 설정하였다. 이에 따라 최적화 문제는
식(8)과 같이 단순화되며, RMS 값을 목푯값으로 두고, 해석 모델의 RMS 값이 수렴할 수 있도록 반복 최적화 과정을 수행하였다.
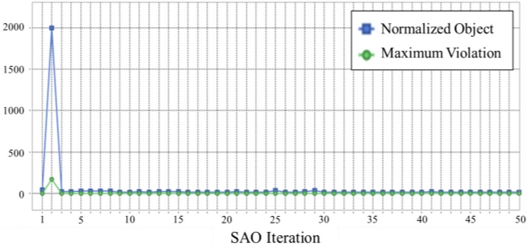
Fig. 7은 최적화 수행 시 수렴 과정을 나타낸 것이며, 최적의 이득 값을 구하기 위해 수행한 순차적 최적화 횟수는 총 50번이다. 최적화한 해석 모델의 감쇠 계수 추정값은
Table 3에 정리하였다.
Fig. 7Object function and constraint violations in SAO
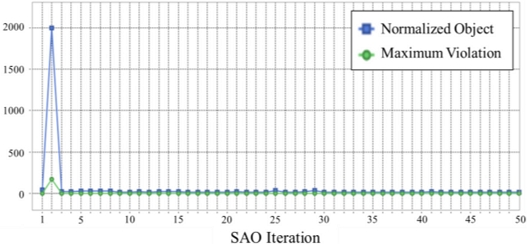
Table 3Optimal design variables of damping coefficient
Table 3
|
Design variables |
Damping coefficient [N-sec/mm] |
|
cmin
|
0.127 |
|
cmax
|
0.616 |
반능동 댐퍼 다이얼 기준 0단계 일 때인 최소 감쇠 계수 cmin는 0.127 N-sec/mm, 12단계일 때인 최대 감쇠 계수 cmax는 0.616 N-sec/mm으로 추정되었다.
추정된 감쇠 계수 값을 해석 모델에 적용한 후, 동일 조건에서의 실제 주행 실험과 해석 결과를 다시 한번 비교하였고, 그 결과는
Table 4와 같다. 최대 주행 속도
vmax = 0.5 m/s 조건에서는 두 감쇠 계수
cmin 및
cmax에 대해 수직 가속도의 RMS 오차율이 각각 2.75%, 2.27%로 나타났다. 모두 3% 이내의 낮은 오차 범위를 보였으며, 이는 저속 주행 환경에서 해석 모델이 실제 동특성을 유사하게 재현하고 있음을 의미한다. 반면, 최대 주행 속도
vmax = 1.0 m/s 조건에서는 더욱 큰 진동과 응답 변화로
cmin인해, 에서 7.26%,
cmax에서는 9.06%의 상대적으로 높은 오차율을 보였다. 하지만, 이 또한 오차는 10% 이내로 확인되었으며, 고속 주행 조건에서도 해석 모델이 주요 응답 특성을 유사하게 반영하고 있음을 보여준다.
Table 4Comparison of RMS between experiment and simulation
Table 4
Damping coefficient
[N-sec/mm] |
Experiment |
Simulation |
Error [%] |
|
RMS when vmax = 0.5 m/s |
|
cmin
|
0.3093 |
0.3178 |
2.75 |
|
cmax
|
0.2116 |
0.2164 |
2.27 |
|
RMS when vmax = 1 m/s |
|
cmin
|
0.4116 |
0.3817 |
7.26 |
|
cmax
|
0.3906 |
0.3552 |
9.06 |
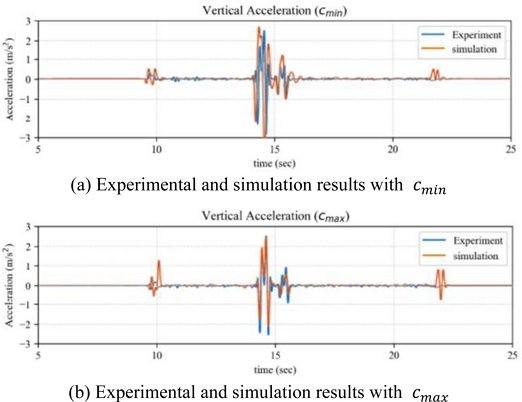
이때의 실험 및 해석 결과를 기반으로 도출된 수직 가속도 응답은
Figs. 8 및
9와 같다. 제시된 결과에서 확인할 수 있듯이, 전체적인 응답 패턴은 실험과 해석 모두에서 유사한 경향이 보임을 확인할 수 있다.
Fig. 8Vertical acceleration results under vmax = 0.5 m/s

Fig. 9Vertical acceleration results under vmax = 1 m/s
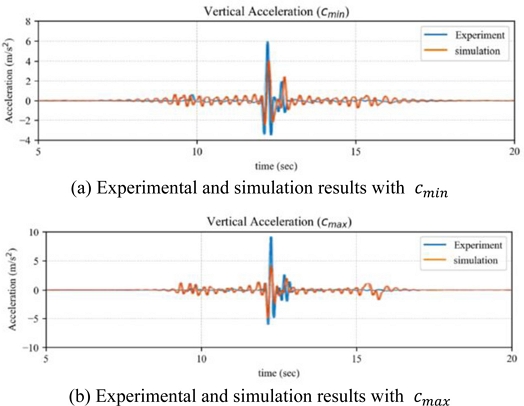
제시된 결과에서는 주요 진동 구간에서의 피크(Peak) 응답과 발생 시점이 실험과 시뮬레이션 간 비교적 잘 일치함을 확인할 수 있었으며, 입력된 감쇠 계수 및 속도 조건에 따른 응답 변화도 명확하게 관찰할 수 있었다. 특히, 속도
vmax = 0.5 m/s 조건일 때는
cmax,
vmax= 1.0 m/s 조건일 때는
cmin 의 결과가 상대적으로 낮은 오차율과 높은 일치도를 보였다.
Figs. 8(b)와
9(a)에서 확인할 수 있듯이, 가속도가 보다 안정화 되었을 때 두 결과 간의 응답 유사성이 더욱 두드러지고 있다. 이러한 경향에 대한 해석은 4절에서 주행 조건별 최적 감쇠 계수 분석을 통해 다룰 예정이다.
본 절에서는 제안한 해석 모델이 다양한 운용 조건에서 로봇 시스템의 동적 특성을 신뢰성 있게 재현할 수 있음을 검증하였다. 특히, 최적화 과정을 통해 얻은 감쇠 계수 추정값이 시뮬레이션에 적용 가능한 수준의 정량적 타당성을 갖는다는 점에서, 해당 해석 모델은 향후 주행 성능 분석 및 서스펜션 제어 전략 수립을 위한 실질적인 기반 도구로 활용될 수 있을 것이다.
4. 주행 조건에 따른 적정 감쇠 계수 분석
다양한 주행 조건에서도 휠 모듈에 탑재된 반능동 서스펜션의 감쇠 계수를 적절하게 조절하여 로봇 시스템의 주행 성능을 확보할 수 있도록, 앞서 개발한 최적화된 해석 모델을 기반으로 조건별 적정 감쇠 계수를 도출하고 그 경향성을 분석하였다.
분석에 고려된 주요 주행 조건 변수는 총 세 가지로, 주행 속도 V는 0.5-1.5 m/s, 로봇 본체의 하중 W는 20- 60 kg 범위로 설정하였고, 장애물의 높이 H는 20, 35, 44, 65 mm 총 4가지로 설정하였다. 장애물 높이는 향후 진행될 실제 실험 환경을 고려하여 상용 전선 보호대 모델의 사양을 참고하였다. 해당 조건은 실제 휠 모듈 구동 사양과 상용 전선 보호대 모델의 사양을 기준으로 물리적 타당성을 고려해 구성되었다.
주행 조건별 적정 감쇠 계수를 도출하고 이의 경향성을 확인하기 위해, 실험계획법 중 완전 요인 배치법(Full Factorial Design, FFD)을 적용하였다. 이에 감쇠 계수를 포함한 총 4개의 독립 변수들에 대해서 조합 가능한 모든 경우의 수를 생성하였고, 그 결과 총 1,200개의 해석 조건이
Table 5와 같이 도출되었다. 각 조건에 대한 해석 응답으로는 주행 중 로봇 시스템의 무게 중심 변위를 설정하였으며, 해당 응답이 최소가 될 때의 감쇠 계수를 최적값이라 정의하였다.
Table 5 DOE Table
Table 5
|
No. |
H [mm] |
W [kg] |
V [m/s] |
c [N-sec/mm] |
|
1 |
20 |
20 |
0.5 |
0.1 |
|
2 |
20 |
25 |
0.5 |
0.15 |
|
3 |
20 |
30 |
0.75 |
0.2 |
|
4 |
35 |
35 |
0.75 |
0.25 |
|
5 |
35 |
40 |
1 |
0.3 |
|
⋯ |
⋯ |
⋯ |
⋯ |
⋯ |
|
1,196 |
44 |
40 |
1 |
0.45 |
|
1,197 |
44 |
45 |
1.25 |
0.5 |
|
1,198 |
65 |
50 |
1.25 |
0.55 |
|
1,199 |
65 |
55 |
1.5 |
0.6 |
|
1,200 |
65 |
60 |
1.5 |
0.65 |
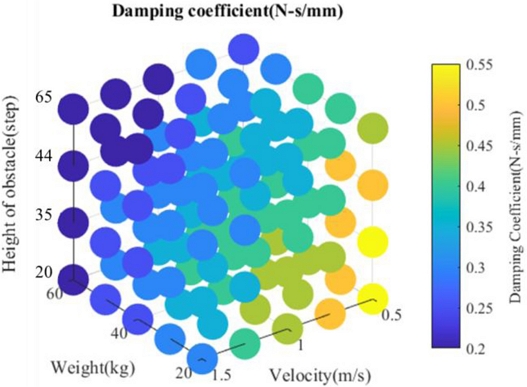
Fig. 10은 도출된 감쇠 계수 결과를 3차원 컬러 맵(Color Map) 형태로 시각화한 것으로, 로봇 주행 속도, 본체 하중, 장애물 높이의 조합에 따른 최적 감쇠 계수의 분포를 입체적으로 표현하였다. 컬러바는 적정 감쇠 계수 값 크기를 직관적으로 나타내며, 조건 변화에 따른 계수 값의 상대적 차이를 시각적으로 비교할 수 있도록 구성하였다.
Fig. 10 Optimal damping coefficient map: isometric view
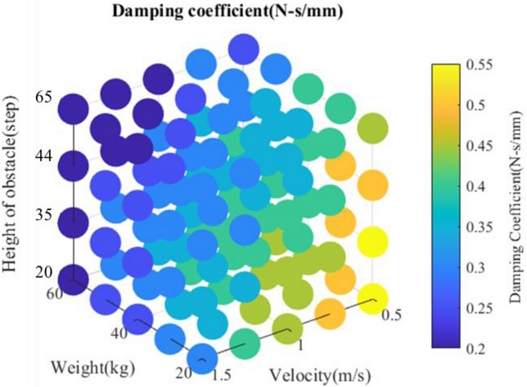
결과 분석을 통해, 주행 속도, 로봇 하중, 장애물 높이의 세 가지 조건이 모두 증가할수록 최적 감쇠 계수가 전반적으로 낮아지는 경향을 확인하였다. 이는 일반적인 직관과는 다르게, 고속 주행 혹은 큰 충격 조건에서는 과도한 감쇠력이 오히려 반응 지연과 잔류 진동 증가를 유발할 수 있음을 시사한다. 특히 하중이 증가할수록 시스템의 관성 증가로 인해 빠르고 유연한 복원이 중요해지며, 이로 인해서 오히려 낮은 감쇠 계수가 더 효과적인 진동 억제 성능을 나타낸 것으로 해석된다.
이러한 결과는 서스펜션 제어에 있어 운용 조건에 따라 감쇠력을 정밀하게 조절할 수 있는 전략의 필요성을 시사한다. 특히, 본 연구에서 도출한 향상된 해석 모델은 조건 기반의 최적 제어 전략을 설계하는 데 있어 신뢰도 높은 분석 도구로 기능할 수 있으며, 향후 다양한 주행 환경을 고려한 시스템 설계의 기초 자료로도 활용될 수 있을 것이다.
5. 결론
본 연구에서는 다양한 주행 환경에서도 안정적인 주행 성능을 확보할 수 있도록 반능동 서스펜션이 적용된 소형 이동 로봇용 휠 모듈을 설계하고, 실제 실험을 기반으로 향상된 해석 모델을 개발하여 감쇠 계수가 휠 모듈이 장착된 로봇 시스템의 동특성에 미치는 영향을 체계적으로 분석하였다.
제안된 휠 모듈은 저자유도의 기구 구조와 감쇠 계수 조절이 가능한 반능동 서스펜션을 통합한 형태로 설계되었으며, 기구학 및 동역학 분석을 통해 사양을 도출하였다. 또한, 실험 기반 데이터를 활용하여 해석 모델의 정확도를 확보하였다. 댐퍼 감쇠 계수 범위는 순차적 근사 최적화(SAO) 기법을 통해 추정되었고, 향상된 해석 모델은 실제 장애물 주행 실험 결과와 비교하여 모두 10% 이내의 오차를 기록하여 신뢰성을 입증하였다. 이후, FFD를 기반으로 1,200개의 주행 조건 조합에 대한 해석을 수행하여, 속도, 하중, 장애물 높이에 따른 최적 감쇠 계수의 경향성을 확인 및 분석하였다.
이러한 결과는 주행 조건에 따른 감쇠 계수 조절이 이동 로봇의 주행 안정성 확보에 효과적임을 실험 및 해석을 통해 입증한 것으로, 반능동 서스펜션 기반 휠 모듈이 다양한 환경에 유연하게 대응할 수 있는 실용적인 해결 방안임을 입증한다.
향후에는 본 연구에서 확보한 해석 모델과 감쇠력 경향 분석 결과를 기반으로 전자 제어 방식의 감쇠력 자동 조절 기술과 다양한 로봇 플랫폼 구성 변수에 대한 확장 연구를 수행함으로써, 자율 주행 기반 이동 로봇 시스템의 주행 안정성 향상을 위한 기반 기술로 발전시킬 계획이다.
ACKNOWLEDGMENTS
이 논문은 국립부경대학교 자율창의학술연구비(2024년도)에 의하여 연구되었음.
REFERENCES
- 1.
Qin, D., Liu, A., Teng, Y., Qiu, X., Yan, H., (2019), Trajectory tracking control for mobile robots with abnormal data and external disturbances, Proceedings of the Chinese Control Conference, 5439-5444.
10.23919/ChiCC.2019.8865377
- 2.
Kim, Y. S., (2022), Transformable wheel mechanism for service robot mobile platforms, Proceedings of the Korean Society for Precision Engineering Spring Conference, 23-23.
- 3.
Tagliavini, L., Botta, A., Cavallone, P., Carbonari, L., Quaglia, G., (2021), On the suspension design of paquitop, a novel service robot for home assistance applications, Machines, 9(3), 52.
10.3390/machines9030052
- 4.
Hanebeck, U. D., Saldic, N., Schmidt, G., (1999), A modular wheel system for mobile robot applications, Proceedings of the International Conference on Intelligent Robots and Systems. Human and Environment Friendly Robots with High Intelligence and Emotional Quotients, 17-22.
10.1109/IROS.1999.812974
- 5.
Jacobs, T., (2018), Omnidirectional robot undercarriages with standard wheels-a survey, Proceedings of the 25th International Conference on Mechatronics and Machine Vision in Practice (M2VIP), 1-6.
10.1109/M2VIP.2018.8600822
- 6.
Jacobs, T., Schaefer, E., (2020), Design of compact omnidirectional wheel modules with internal differential kinematics, Proceedings of the 52th International Symposium on Robotics, 1-7.
- 7.
Grimstad, L., From, P. J., (2017), Thorvald ii-a modular and re-configurable agricultural robot, IFAC-PapersOnLine, 50(1), 4588-4593.
10.1016/j.ifacol.2017.08.1005
- 8.
Xu, R., Li, C., (2022), A modular agricultural robotic system (MARS) for precision farming: Concept and implementation, Journal of Field Robotics, 39(4), 387-409.
10.1002/rob.22056
- 9.
LiBretto, M., Qiu, Y., Kim, E., Pluckter, K., Yuk, N. S., Ueda, J., (2020), Singularity-free solutions for inverse kinematics of degenerate mobile robots, Mechanism and Machine Theory, 153, 103988.
10.1016/j.mechmachtheory.2020.103988
- 10.
Jiregna, I., Sirata, G., (2020), A review of the vehicle suspension system, Journal of Mechanical and Energy Engineering, 4(2), 109-114.
10.30464/jmee.2020.4.2.109
- 11.
Soliman, A., Kaldas, M., (2021), Semi-active suspension systems from research to mass-market–a review, Journal of Low Frequency Noise, Vibration and Active Control, 40(2), 1005-1023.
10.1177/1461348419876392
- 12.
Jeon, B. S., (2016), The optimal damping coefficient control of the suspension for increasing the driving stability and maneuverability of the rough-terrain robot, M.S. Thesis, Chungnam National University.
- 13.
Heo, Y. J., Jeon, G. S., Lee, S. H., Choi, S. D., Jang, I. G., (2020), Development of active suspension system for wheelchairs to improve riding comfort of gait disorders, Journal of Biomedical Engineering Research, 41(5), 203-209.
- 14.
Seidla, A., (2008), Actively articulated suspension for a four-wheeled vehicle, Proceedings of Nord Design Conference.
- 15.
Lee, C. H., Son, J. H., Kim, S. S., (2021), Validation of the impact reduction effect for tracked vehicles based on dynamic simulation, Transactions of the Korean Society of Mechanical Engineers A, 45(6), 507-514.
10.3795/KSME-A.2021.45.6.507
- 16.
Cha, H. Y., Beom, S. H., Kim, M. S., Lee, S. G., (2009), Gain parameter determination for the feeding speed and skew controller of media transport system using optimization technique, Proceedings of Transactions of the Korean Society of Mechanical Engineers A, 33(6), 607-613.
10.3795/KSME-A.2009.33.6.607
- 17.
Lee, G. P., Choi, J. H., Lee, S. G., (2008), Material Property Estimation of Paper for Dynamic Behavior Simulation, Journal of the Korean Society for Precision Engineering, 25(5), 103-111.
Biography
- Seoyeon Park
M.S. in Intelligent Robotics, Pukyong National University in 2023. Since 2023, Researcher at the Korea Institute of Robotics & Technology Convergence. Her research interests include field robotics, robot design and analysis.
- Sungjae Kim
Postdoctoral researcher in the Industrial Science Technology Research Center. His research interests are robot control systems, control engineering, intelligent control and robust control.
- Juhyun Pyo
Ph.D. in Creative IT Convergence, Pohang University of Science and Technology(POSTECH) in 2018. Postdoctoral Researcher at POSTECH from 2018 to 2019. Since 2019, Senior Researcher at the Korea Institute of Robotics & Technology Convergence. His research interests include field robotics, disaster safety robots, and robot system development.
- Murim Kim
Director and Chief Researcher with the Human-centered Robotics R&D Division of the KIRO, Pohang, South Korea. His research interests include robust control of nonlinear plants, time-delay control, robot motion control, electro-hydraulic actuators, winding machines, collaborative robots, disaster robotics, and factory automation. Dr. Kim serves as an associate editor of the International Journal of Control, Automation, and Systems, and an editor of Journal of the Korean Society for Precision Engineering.
- Jin-Ho Suh
Professor in the Major of Mechanical System Engineering, Division of Energy Transport Systems Engineering, College of Engineering, Pukyong National University. His research interests are disaster response robot, underwater robots, and system control & integration in field robotics.