Skip to main navigation Skip to main content
  • E-Submission

JKSPE : Journal of the Korean Society for Precision Engineering

OPEN ACCESS
Search
Advanced Search
ABOUT
BROWSE ARTICLES
EDITORIAL POLICIES
FOR CONTRIBUTORS

Articles

Page Path

REGULAR

타원형 푸리에 계산자 방법을 통한 나노 패턴 균일도 분석

황준식1,#orcid, 주하성1, 이후승2

Analysis of Nano Pattern Uniformity based on Elliptical Fourier Descriptor Method

June Sik Hwang1,#orcid, Ha Seong Joo1, Huseung Lee2
Journal of the Korean Society for Precision Engineering 2025;42(6):477-482.
Published online: June 1, 2025

1 경상국립대학교 기계공학부

2 충남대학교 기계공학교육과

1 Department of Mechanical Engineering, Gyeongsang National University JFIFddDuckydqhttp://ns.adobe.com/xap/1.0/ Adobed     ! 1AQa"q 2#w8B36v7XRr$9bCt%u&Ws'(xy4T5fH  !1AQaq"2B Rbr#u67Ѳ3sTt5v8Sc$4ĂCÔ%UӅFV ?_Aנj- H>>,m*>fzp"TrKkr^r.|_&]|*vPuܶvoQ1mwVJUhu-I"=LniAƕ8"۲ k*ҿ[yu:.vUQ+)%F DHyVBk>Hy8jݹ q~9D4KRmzQ)^ʔ.J%k_tVi5NTjg!'ky|5asOȻ)R۸ߩFMԿ3L4j6dڜ#NIwUF]JqB/(FafJRzq3\G՛ ?~\ 6)6W4m[O^L0E&rRMض*C .]Unl-1 1r#Rj/&QɈ׉˩s6Rj=5Tg.y.·Pӡ:JJS:C8-2u]d&vUz;7p9 5VnL֢"y)">iי(IDDd| Yj0; LRfS:ktYK%*N2^m|&dğth":ey)uPQZW)gcC3Pv&MMWd&Ŵ۲mvTRoժM03*F3Yd6\8,\hݻ kߔi<k NTwSԪmljj[>->ptU%'LR>&EBH$MQAUx[$Z6vi&_a.KIQ{hyƒ j"JOC9eFҝfj;˚Ω<[3_m% lQ@4g=5$(J]Yc-OMq<Ǎ wSzڗ)k$7VIP붾ͯnV+卵*t]iЎD31~SA1éC2u)ʼnQn-Uoi3:grI8ؓWm*G zܕ)ZקJ}Y YlGeJ6cB2I NS3Q>k=KTBT]W6+SOXQgGR? telˊ%-Re\hѯ2TF"C/OJΩ6r[N.0{SpljjX1“jOsӥ;ҭhe}xu`Ք&.)yO̒ Fߑ.$Qw;9Iw2o+RVJMSOj[SoҌZ%;`d$blQ{Ro{Imڌ>3egf\O֝Uzx"䢸g+mv%Gʆ:|V[N'&ס-ޝ'kfE|K,G&˳98Juin/\\Qݿ̋v~Ǩ!rtWU d|E߫R4d}.qPw*Ӭv5YEcn~f5c%MTMkb-F>5JT,})QHg%{("ӔȸWMsYyWNRrkkJr0XドnͫT}r-jj,Ŕʍ\Q2Ri>v$5!]"JB2WɅ)]VԜUc8i|.jeRO6^V.¸ Q&#|ܶ-*uOG%JAtRZRr]FFG\۩w+?'zչSѧt jz>KW&ot{7P&2D;&\\>Q2JzܗAKSfeNn[jRrԕf6,q,F1tRfԗ>vֶևj-&R'Zi2=xv~Elbsvm8=ӛ"ū񕜈BȩlWau[]ٷBߨF~J!|Ipr3R̴#Yp)={7:G{+:\W}n|Q#%)7^-h"Ƒq:M*%J&$T軨I333׎g_- ucBwwjp[6i25$̏bU’ٱRv?G\~#Iͪb7<<}Ezt" q_Inw,7-d,G÷%T* Wg1"䥱kq/A.,_KhqŒxwvo u2ۥۧ.bQ}XκA$֣ +K״ZUNmڸII{.v{5z5ѮRme[moyƾd~cRݾK'j.\i&/S6f|b=5: p!6i_ 4j6=.si˧eƾtS^c.Y^RJVS-Vi3,esi08?H$GvZgg?gi䤟2adw릿:"۪lkSN>q-4kI܋ێe̊qۅgDoѨ9; #T.Q;7#~_Ufstb_'w~Xw1Xk,vcOt._}v}8"(4Z\ۘgk?J?bm_c!g{HZV]Fkk%~gEt)b秴vΰB|꽸}mp~E6ݹv;7P٤v+ri*3Ԣ|'O14_~7nP{7ZU\Vű[ +7󖱅o#:ǥŬ\|3r%TJX]V7ez¨Y]lc|O3V! R zbJ'PnGqVJ"19WVeOF埜EaEJωqCN5Z g-9[S<$sUK5b|7sn\7x qmv##FF\ w[=-43$^ooVSiXօv7iB۴yg>]Vf"r$J3""32!Zh[K%7GvNLs+4nB/B{vlsobJaҺJR:0g%&zR\ S3T[&ִor*ⷳc3ʊO[iozW٨%$gn:ܶWwFBԹjHP&z u&F2\f;ipW73 [; '_̽b;vib!oec dC-tS__$Xs]l9&z$2/N>%'[}b{h/{`{Ji׉׏ YJB/X%}.|+{(S:qz]4_Kѵo`^tY_4S#* ^zvݾMr+TrkQ g.8Ͽ^i>ӈǙvix>$o( ^qt*&t1oJVu-ql5U6jCЉmĻ*"?JT=K'O/|=Vo}l0b}}f?X[?/\JSBe,kP8ETJ==?.p5ފgbU9}ǶdNKk—_$8̸͓ۍ8Di\BԿ-1v{FF]|.^ۅ{vl12׏z7-R7wE?\nh\jN/Kձr_oBw"N QMBZqe-m:ӨSn6j4%!hQ;sv'm4kcM=!8\m[M4{SMliۇ%eֽR&N:{2A8)THLK3Zj[jPBx#BگMf:G1\`edcʮ?|w(-̮vXt,bW2;.ιNHRR#YwTM"<;mk\.foIDjmlJ;vxy7o7i\,KQŊ9d^Mmgc L*.T6tLeIuOH3SJQ3=F/ʿ<9\JM6mN6=<{xkP!F1QR[I$6ُimXu2An2yԒMU q f[IB-'䤯jYm52&JG\zд\~vdg QtHGXw&1Lw+nDEdC1w|YJmvP)HZ>i0BPβә?R:QO["]I_Jʏۍ>QKyu^bycBq4lXF~l [\*N>-J6,Gq(Zr5h]CwYӤU~ʶߑ u*SIv%ZfJ7)! FS*s_\|IŸZ)J ]ܜi4"z[+Z,MOZ))}|Ʀ(RUNIII.S'ˍO~˨rn}M)xxӕ0 eyҵ7YMAB]ӣU:/ѭ*6bcwP͵ "+qēVjŹO|GtY4V j[mLV M -m>",B$ GD1~j6O4|LxnNmqATNR3ε|DŽa[fmn-ڭ+FiK7Pcm;r5 l8r{#-]'nrFh2ruycb;pW=njRqRJ(d mnpckNnʹ+6]tz~E=ʕ l ZZ5jSi3#47.Lcfe`9؏v囜.F\-UZ:*0_<Νu9Lӵm&)_3\^ҹ3"1n1v_|uRʞͫr'iȧN_kH׺8xXrj=\МH)V\ˬ.Xʸ oVRC}ySU9/OBY먌5 ٿwޞ)rw8Ӫi5*5ZΗcGƱ !ZۄlmpjJ -l <R̵/JAպZuq\IdUS 48wXJJtcg4cI~aqߓwŷrm-v)G7yS^7H^-\mŌAq|"m9IBnF㏉9[N+mmy/!KKۉ%n +BdddfFF6FQRN-U5;Sv'm4kcM=Mn)\qιqUd9F%",6MGdT%-+~ f%+y֛^3SrF>6lc(֪vۊN;g._0Sѧ]ETWرkQKzGe9ʨsKA"yC y2\[5 rԭ7Gk5Mzw_4sM3hxЊ'oÍ5jsub )ͪ~tR2H]R͍>̋m6=%(˿(Wrr-܅y5(ܔJ޺YunW̹븹NsqK ]/QR#"ZMDfD|43Qw|._ԡSqTZBg??O Ϥ)/E_U|i}2 9Z?¹0:x'3,whǣ?C y-A~=daJј&M?D1_PS+Oi&;a @;Dž7[ zZC"bv:jjMQk$M RԸ3uA\=wI.AwC"^.{?-\NSiˏ"b}T/}q/ o.1M}R%:-ZniʒL$SgrBW*,Mw'N\ɇ{s\j]VryG'8f`}'N<*/`U숻z CwHq18J+vԕKss4R53/&XTt1bZƟo\=%nO)h$rBi-nKĪ^ ջڜlwkYm[̑+/QrZo%TQ;TLs($2C:s.%+eoNttq۰kK7O0m_t_pZ1SsSM7"mevFZ[w -FJ*T*jФQRg BSu|]g:ɵzjqwmltL.e3sRMچkSmjkmWœިm++¦'tILk*բQ D,PB\lI[9{%Gb R6öۍmX-MaʉA931cs..G4CujQտ[9 }G-xwl)IQz j Ó"rqe&=]꾧֎c)<kӳ+0JrRR3'TnXi^xMF Bު*tIL.[h"2"nKzZe'ZV/RrNYz]8죝n]Ķܩ>^Ժ]u-7^\mZjܣ9+Rmn ߑv?oꋘ?&ƪy^N4o=3-ؔ̿*`}V݁ ƒPu8%$ ݗ]wt;\y\>='OjPIp/nJU8{϶FNMsf"ίNqƹ(+ ݮF2Km |jܴZs%zf*eȫ?]4)I۵nR&FX + [jDh(#哑9q9Eծj8noǕZf\J-l&Z˫}`ӎhyrΉn\űn]9pʌӣ"׮Wt?N4_I_~54#/my1Xr*척aS#DT >q ssΛW;3oUaJSRMDgQnt:Ql,/ ܷfRqiM Ȼ>Cob;A>ڦWقM9X~/!'MW.}Vrߔꔵ!5|iB(0-zF=}okڢE$^wW~nokY߮\6՜̌{i-AF*9)\t9IV6۸5ZUF6R$ŨQIq砳YUZ]eyv >hI櫥N )&l JulwE1GDOuFN2| }馥uC1rޫV+^gdb&W[4<^e4YW,d|htͮsUM)۸8:{3d{AѢ)~ \#J=NdƮꮓ90 |1K$v*?мS ]i$J,C,SG?/_՜pMSƯM|mG1V1$~K>CSvkuj=&) -,yLjuFHK{c駗.SOua;BrSqj-ۍZ#'Jys7[g2z/.u4+XV2VQ.ޕ)$"(%)#Z7suZ%j }BǬݕe)Jvz8zJf:hIN|svO1O#IEcۍjݽ:SdὮvu^@:o^5cs>i/VqmVm]ؔܢn6'vޑ̗J4Wn@OlKbX ;n:hgJ9ŻyǑz8f܌q&Y fN0N;[69 rbׅC2/#kE l&2~èMR.*%g=Ft.%؝e8<.e=Uv{~㻏"EˑnvDѭ͜Lu3u0:U֝$[M5<:oi+V4V9 6nXvx&_ q Qqw3W:uϔ2yb/(ɳ|5zQiJ#r|Hw#.W?4aDŲ\ugWG;Cw鐢K|xg)##=O.dF˟jMUvWĻsr.z]kPc9"]R)mkfOd*uYf١RsB Aîh=k]ʳUrrZsq`d#r$/Ը3o^&lRWȍyuW̦Y4QDUMJ65ƒ[+ygk XK_±k#y:8(TJOSQhJt2.DR}"5[) r)6V6u5k:eXZmv𭤔!푊Q[qQ}ҹLE- 8qIZG|UM4j}Mܕ[Vwm{} Naqµ"ԈM zOpKѰ?IAD3Ir0'/q1itoB5{%wkOBn-ۜduqIzYK60{+DʕܞqIt";r1mG/\/ym[6JƫR \L=S=OT@Ix[TMm{>ݾտ֒ݸӉLYIx>+"JVNzx||5rI?C{oz8۹e\R-^\A2F R+N9 vlT]"ۭ d)t֞i #E2jB@׵=#/N+!ĕhx}I!cM`ąZ*ŻɄҒ߮Y.Z}='/oۙ3IpW̮hT7cTSuz9>B}΄&h!>lӵn~j˅IvU.'v'CSZw8QK3G> ,J59ٷ+HSg䧎hJdzvwv-cvxS5[̊n~ؿ%ַX?O0\6ne 6kn9.ϯ} *h 8_QhLݣ7q +=XBҲ5?[[)+F`=4 }B,sNg==u*Nj9k_GJ)+R~GSPBȒZ:(K]heL=vKPӢwq(NrG^ثϣ?#tC?.ͼ[ۅo؞y#%ǛjVyLSw%T*s92JTM%"YkQО.q)gCͲn8cgi6j1MѾ[{9h^vƘǚםidfi.^RHmg&rׇz:}݃}xT$ضk'5s-狶,\vpbPD،=Okf.c#cdz2FK5T!&)|ntD<+OŹU i-G[EE*FDfeaf2QƤM\UG_{ǹm%\yrGy:.\4wjPGUJޕUV7Do\7Vy_13w;[?c]H\$IJ,*L]3b%L{y.JRKG2sq,B6T}(#nW|km+q5] r㪍bJ@y{byz,b踊3ϻJ,'^xd،)JVw#.Vټc''ÝպWtbRؒJz۠8!o9IۄS95E9ؔ-e9JR{dmnｯ<[~n${~Њ$W?&ՐY_? #a.ߑv?oꋘ?&ơ|y^N4o=3t=~7!/M3>n8W홎2M`Qx+ z qy8%]7_~540ۦ彷]Wq CѡwkďyF5Dum_}~P(5.(X,K9vᯐ?leB9;Jhm#3{CxGE-S{;@Fz˙]=O'!ɿ]' r`:7'2bЖ>Iy,/eTy/V<.H?UYY{\^#ѣr9^7?xoRȆ7EoS_&??zϾM?(~Q-K&>"~aߨ t7Emsϛ+?;fCr)fY+>z$tIkjn_>vnrֳki-˹l= t;'EyC¥|/BLwBJdgjۛ$s S1|ɍV%JI6KvəhzIlBYɒ|0"Sy0F>eo5W)O+X˻u';v)2vVq۳kۮws?UʑBǴYO漪e2MIjPAک\b1)DDؚKm6ZWΨgȕ۶yjڳ 2ضN[C[|r@9Jfo<_eI7q.|cÊV߷:i.:$ȋ)1%%)ADZCEBxJ0MJۥy(bNsKM9k43IwNt.\%N簤I'.j|ƃ2$grBEٌ\}9:v*!n7M(ɽ]7c@XxƱԨ37īf62cTTfFK]9wntQHͮvٱI/f|j=7}\_V5U^+:uljSȃY(XI.ȱmo1甅jڎIZ2>#\*:gY|4k\8ZwSqtyA!+];бޞKծË¥e)#5ap.QK^8VdU{*ѽL\=qmjnB5>{ Ӟ`v±5 ^k&O~Oshɷ,;6nOW>u6{RqS`)S%jp\ipdEBLfTWy$GIYw~䲭J.1vSY5z.V>^+Ǎvc.I[R{QsNR3ӎfhd>y?UJ*}~[e\i5U^͛E]G_FS(Iɿ]i8:4zj~շsW,ˆsy:%O}iur]iF5~3M:Ӟ#N06)4ߧgdawIotiz:1r5YDZLHBSi;NQc44la=Y kQIT*ըl:tq2(է9VO4뒳܂~2rq'nrVZŦ[t7\oլfb/mlpc.I8콚q^1iE~䰳mi[dۧw֤ICfdFeCsg:i| 6擣׋* 96lust^{%99UNRvaMܽo ammi$em4D6DD\nA%$$#}۷/ݕr99JMն[oT޲E"KTaP+HGkŴj5TM5xƱOS-k`ۛkٝWz;{kS}F;~q|~^_|euwnE'pSupUP)V]vE+t =ZRaVdG6= *.ϼnj9:UɷbېmF_tޫgHjVS'śǕًdkkѻ_]Kv?nT>)^e=Ar1'3ԔILyD?:-^in):{7.؂\.:V }#뺾.3r̸*xbFM aȵz 6SQ:ײj[ 8nn iFMw rR"5M5I旘35f^j='j:nNW.ʭocZvZKV^ɚJ.cM1ZI7E'6rg탸5oZ=[m Z`\hbMUR١Ȗĉ):Jin!_7Dй+f̷eKҷvͨBPR(V`y6tw*MRΝcB.ڭTnc;P$8nFvm4(D(R#R-L -2:FP lxZKQc6I("Km%$E, 78uXIFA$RQI$JbInG]c[ֹ:ZM+n^')JmJMJRu{e)7jQDw~%yQl}BZujSSf۩QZ+Dzhd5o%BIc'GZ?}΍:>Ɵivז-%݌J5MqGWTVʦh݇ܟ~Օ_6 n'{3~mϬj'J11OȻn߃r Qr\3y٘+WӍ'WxEs^O3 o~[|7>]]H9݇ZomT@]?5B:Z߂'`V_+/MSKX߆ޠk3?o7y:4R/7þ] iG߬aBRU&?r&/} cQߥGj2?C5Yśe7hU=?+ x龳f-܈czW^7p%-(\D4h{UK&ӡn^m]Fݢ:`δvj俜F+) y[{{ 7 tu>gvrěOj'5 iRg[ͶFjGe n~qT$ci ۚ0oԹc*jL[sVWqj\ݻ&6"WoK:cnWmrv)o>66(F>=W^bf#c zzʞtپy%mՉPël e}J.\Zk4ttt>oEM=q)hJjI=ͥ(%]脼_88ф;͛gWG;Cw~˘$4=uWdĜTثNDkiQL9U*O"4XP`02,Ge-k5$h>ܼ]3vr6!9RQPIVSnM(ۓ{>;/Qͱv{3&-[rc)ܚI$n{Sv3[j00)-D3z}MRzVQпj,T[uVs0\}Sid;r(ݝJ>æʺL&c[jPK0~d(FKÝW\m]GTcF|Iׁ)I3~#oX%vҦEݑؼ5Żv2qAZTE^..M{ʐfȏ2##.R}*KʛZz^ӞN*lPťLf\G6[WVQquV]XAi)5J!,$iJ6o$tPZc;Kjx_n3`qIelV~vLy{fn匋Ѿn%;zV.n'-ұdd2߽1bZksPe3TI9)$ԩIN9Vơ\=2885N\ p)/a柛w9g_lױo8ݷ iixJV& ғRi{N^_oAŮE6Y7I$Nk$|Q)-*4Z)^¸%4Qm [I%.c-OV+C֧R#%ѨCe3i;w$G+_dy| Fzj$DI(=OA gj%v/]8qԯNIS*֩',Q%\44ZZ%D|Ǧʴ6&vֵI$%8(ԬƾS&#Z. }6z?b/|Jl{ץv&mpx4Z$”ڝ4-H%dGKfM:sKSRWeJAn]>s6应-W9'H]'uȫYvgK^\czp|My\鏩w/ËQ.)]\QiS`8uL뚛̸=J"ܻi\å'-)54Ue]:K\퓡vK xwBqrH\*֕TnzC.mT=t-H]SČ~Nu╏NÅ3f|͡G~B+Xm[Q7U{9"~jgK Zoʰ7"qJ,ekSeNGgϳ] ^.6:s}_,%eRg<5⿨z{ZPun#jRІ.6g T.!]xa c#jN$Zpl̋H WZu8WmMRýsĮ?Mco~sx TU҆Q :KDG4n42.<3/'^?6/ܠڒ^yrrÿr2\D}}B]^E~^T cɛ7϶Y[<֞[7d}2%QPqOLEQR\CIsj1?\}%tJ0e~ *sk"*)&ۓEi#{1J8Hrt|'ܝRr8)=ƔN'RVz:cf]F7bZyZUȘ4x8,#JG̒?.W9XnO]KO]%]ƻ O5Γ/3qÓj؍/r̺rƵ 5\&m6h.xoeX[=<3%< lZ"2h\Z[&jW3ejm?k&[]ųj+{N{66leu_+lj]q* 7g*knأYv= q ەdxЬZ|%GUrQ3jLŒqET]1% qkXYūYc[7Ś]QY\jko\</Lc7+'hMSUc6qXyؙ~6#ѯv.0$BQi5YyIhɍiy=KD!n3Vm[V%W-B%swa97ajۗ m+9~]fKq|Ddaˑ0A]_v޺mM5* F-BYHJ5}q>ʉ.6hyDmpD׬'-_v5;5[8K[viJ.3dR:oYHHh9I7:۽fi+wm^ [)odPѱ52CZUJicSw\&_s0uBȍh32džzQflcd^m|7GѹE!fO5]]H9݇ZomT@]?5B:Z߂'`V_+/MSKX߆ޠk3?o7y:4R/7þ] iG߬aBRU&?r&/} cQߥGj2?C5Yśe7hU=?+ x龳f-܈czW^7p%5|Y:SJE\U-(a_cƣUǽXXKiȞNlmۊڭڄR!**ܤMeȽ$|X5(Ź\rJ~ܮ]>'HB0cp XFr_c?f?7<ukSgov¥iG>>䙗i.+t+bOjIܶ . i^:nm}s}(3>NZ$2Qg([".>i.ƾ)B̋M8+"- >eE6DݥJnJˣt׻ 5.˅nJGwZD~!i۶a,Db3ZQ3O#KO5/֍ozuK'GbRi᝘NV_ҝcvם ZoX}F6z 7e5_e:ۓj=AB+iܔERadMBq*ԯ DwI/Gy*mĥiRKg6skY/#SN4e$-yXM YL?^ĸNNӪ{$r1JJRSLO]Aqm>V/s[~i/j+m>z}eI"Qvp]{ZԼ:{vPAG2=T͡@ڐ#u"E*>C;o$~C#_d/HBq^YRٽzIKbOm\~żjFFGdiQ(*/i*#.FF]©m=BmpQQQSP&Ҫ!T&^>:y)$ˑÐFčI Bӡ-t!bM WҦŶ'UZ=}zvn~oT/\ǒ'nr8 AJIӆz<^uߖ4eFC1i+v!3qNyߕni?4JZlmYFXFۼO0B\m[ tʄU3s"Sr(NJ;SKW72L4̏BVdf^Ҹj\]ȱ۪(ӷm?J-KEmWڽ^4<8qu%9pŹW~877ܾeVгS(յe^C]yX͹! םm4FGȋ\y'Z FX7e)|Gjt߹#gb\ŧq_([R8[qU$Z (ʻezV2V!iQ,i$JE˂٩ a(GK'O{vnBvryRd-RK4=qxZJMl_CuuIz @Rt㮽޳!|68\-l[џ84-2Pu" RJ_^OL>G1~XnBŬw6J0*Uvlږ1N G1q9IUm*'oWu][&UyYZbBZRZNfEJf"+2nF~Eû7n1xv.RUM$6 lAxSQJ&n5ܞwlEói"#>4׿Q.nEq7Oko[1wg8ZQwZYiqtm&~">Bo?w͡ni2峋NCEy Ҕ+%ZJ ʩq*fpˤl,~^Mχk1+:ݕ z&Y`KLӪУDr3[*Z :(SL&ݻ۬Vqsyԭs x|iI߽zZrg.:mp%6ԜvgmpIUt;QbS.Է) ǨKSV,*lڌ|5Jt3#NP.=+OZ~/G سIgbꥹJnl_DUM\iM!֔wVZuԺ,yV.Q>f v:݇WiaŸN5Ҕ[M7SsrvǣrMW= \8ZW-jsnڕ.ZnF2qt ً[ٻޘY۷Zm"Jxr&NAfA-݌to9s359݆mZ+N1-qS$D=17 x׵+%_ ve4ir6Z$FDڗnFtOr'7'{9C˨ꤡaYoace{Refnft RR"4%ʌm:Sj3)OdInTO>X'vxV#jܮw9Fog;5.~Y5\~18YQܹvj4+~t7S ﬕs %^۵ڴDZV69R^Y+rj$ԇoJKR5wB9C>Y:l+EǎS{ʲ{T6Wi* ^^9k/y/Cs\g*qڵgn4T8mERr|Ti+iPe;;.i\EBEJ 丬i9ɧM-ԼsGDrZ>r#R>~X9y4b棇9JwV۔%m(b[Tjvl}۩~nDԺ{Zo-YuK1vx.nWuO+jN [ٮ0%"΢CdTJK-RަH"$I(*ve &҉FzB,_Vpqp9m8werv')E;o&QE׵^d9˦j\_,ڵugZȻ̧8k+jK{wmr@3ӭ2 wFkzFVqs1؛.v'I%$[iT]D5Dl2 nk7qUxԫLS+sا3/ΖeZYK<["%-g/kRs:f3;*E ت wJ%)5&+&rw*霣i|sMҴ|;R+fm䡩.!**dӶ-6s6,]zAXMWjmnz%SJߴm2UXw7MQ%<!tKys#P,W>s;3IYwx<+i_\\\U6 u7P|xbn_k&ӓVOe䦒 VUr,-㘘"-LZeOSҠթrEvq8Kf%5%&K"#%vD/.ZYYŏ+p$nZkvއuW9㓱Z G wYIFyf)?ƎUm5ԉ/'k84{KO:rQI}XRuԪ|*lu)3qZ[mSm5R3".Xcَ5c®ࢫI*۳~wRϿQWޝ(EJrri&ۥ^ʶ齲Im|[yb;mnm֩uiܘq>E+Ikx߄3r33-5𹻖09ϖ9[Tz~mr5NsWl$oPusޛ^{Z;);sڹf\3oٹZmԉ/'k84{NO:rQIBø8Bݱ3n֤DiK4u& ofSȒܩx<˘|N0Fչ]qsp"}! QWw@t4ӭ+cO5%]'*{eM߲DRO1y*q8w++e!c߶ܪlZWّM欼 CQ̼빶lX{vib/V/ ai;x6~]+z]MWB>re-:lgk}պ!#9?%܋V-c[z!W?c7YNm/jRr[HOzԻefճ0q15Zp#rkQQ0tU-AmڵP/cȕ?0cZYj;:0ZM=D6g ?'UN+ձ[K ܖB2'xq9{|۫N0ku 7xaj;n\ 2[VznMlWiKbSk))f..)Km)&bGZ=>OR܍W:j'rM'wYz&/鶧{Sʵb"vջq[I-ՌZH._x*BagC'T(Q:$ͳQcMCKy?3g'ߝqnT);qs #ؤZ}OOI:cfnc8W~qy.;^pVl]Hԓ>^H^@7-AA܃nmL(uWܻS߿ Td95Bdh4t6*dDh!EhI[iŨ\L.&Nc ܮf^;$R)\rip9I|ٺ?#R.ZDZ;/]nݻqs\QE9M&Bd ]N mN*D>tgbK>+ˏ.!23]BȔR1ɝ^j'k2ƮqBQq[$di]icV/e`޵B.FIIJqbi>Ӥ|p; 6${)RU>_e}^dzdfzi %ekRVUS?6'hׂ)5.\+qUgzE2C˷ecŏ^֔ibk shesFWJ#~> Wk~ݨ}ڶ>ơǚ)׽ZƉo~B-ڼrvoE:Ʃ3ۣK7+Y`WirS):{>ڛ}:wԨ(J_";6R%[u&ƫdZ_\'np| RJwNeTW,=rrbnkڄ[M3ܴz)3- R.?:okۼ0TU'w{6&w7j1z3ON'fGoO?)S_bQ_¿R(^ԴԴG.EtMڇ&RUiW uQjU> Kiu1d<ѥIQ'RQ1:O/lŗᏩiʂv&Jc{D5 Tt)1.n[n۶X}RjqnOʽ(~[Ns{ސ⛌uO,kgo֢dRNQȄ .'6W!׌P朼tdZjFGE"]K@'i۪N;sI[{SOzk>`rRR+!σj8&TjlvA̷Q?HyjyLHNտJMjܶT۽lG?SnKN%<‘ nq[N0Sq[Ta(&t(|HGO~gvkݻTR4&Z$#ViOY1r$6YF?e4U/Mvxų:zbU^gQQ+NW_'4jfz^c'#`rvrڡ(IJ/J ݦ6 ]-CW |_{v*_q3^DZ}Ic6Uڌ8p7{crZq5ki`)mU6|-Z5^iEz3P=:Cu7DF'k%}<C-޹ֲ̱#\,(f88%X-N(ck0VLR~} G"-8ӏ/ϰKq?(#nrVTmZ;zióM4 m |UT'C^_1X.gXM{%ʤd 4\ovN":"y-,T)fLQgۢr=/CƹǨJVr[a+!rT|%Y\ٱzsS>jͱ.oOc6f$q% ǒGo;n[];ߎjrk{~\VۓNIGn:iqxo |~t5)Rxעri{Vi&NUOl_ѮMfsޕkЄay.0P{7N((BaIP$ K"U6Gl ݙqJRu+qN$ m#*p<|{:>-Ev=86N*MM긭U*uѾ?/^o7;'u,h4݌xښRM:5.(/ \իU.{F^rmF-Jɷ.>Q"[4xT^OZ~mK}T0ݛ^SAo9u?lX(' qj%=X}"^e4wˠ|rܫ 6I\Ķ;Ӻw!'ڍWg{ i U_9Avhۣƾ+:vs/MK[ɭīe{`Zgb}r[i'GE2J7Nez579wRq+Un ]J.cJ4M:h箽Wxxm^ pc\wcN%'My $$| :$Fqɏ¾^қP9J6Wxvu}ݵP>Z'FFdg"-; [¢cmWkÎT8nG%ݣ7*\խCLRYZͤiD&J#'ehbSyXK|y*ӞpS̍R`[pTr/Eg)K+92{_ n3zwz'oŸۤ+sOj J:`T>Cf*lwd\fYOP"R E֢̔L4ɥ :;.b(B02rJ蠟9>V'9M%)IqnhP<%,r'P/vNSwr#w"ݨaqc(|{kd=^0jTMR2ULNz|.<|^PfY22##!,K~E BEJۜ&jRNsHަޛg\r,v؜.jK3)[EJ2ii{KEiHP^&]Gn8x=K}Wx/KI9-ϵwQ%spܾ[^R}S3$qvq8M[ ozKxcqmJ/ӿ{_}7&ݨ\f6ZSyQz& 7ۉ[8~UNn|nkiTB+4RI8'Nc%tn{!]Ȋo.nEmʱn𵵥J A+wy#+ikǒڂ;՛s85'KmE:Ђu""Iģ5p=БbTY-ͽڔ詻ngL2Q}$de# fs^o{DUUsfwӶ;s1T,ǤtޒQ\෼J=.tKU,7čJ5 N$y3kdSMQU~mO[03 $zAڟsF5^뜞"Կ QHmrR"ӳηer+ҔZ]hE-6Jmt'ޒ=O[sQj)6K}?e4v_KfZheޓ=BV[bY}lݒTTЬ{ȫvO_qpRApVŗ 6ju=*BR)g "O1yhb=tqJ gtm\b3RY+JQ^Ō֍\յ\>+uSi{=x ^w;uӘ#ĸzLn*$anok߷CBӷ}5Yqvdž<( "_OWit5:EZj2 B ρ1̊fi[n!HQF82q1牙nqnEpT(2RMoM4ϳOu ':֧_Xjsg jP^(ڙ{2%E͖j^}ZU[Q$'U) <܂%!s"m R'G5M0<+zM6qYm$ڕ$3ǧH]?o2N<8F1̻r_my[Rf59NjpzBnl7*{.QP 3N&^BLJPjAHCK2Q}$#~YMq8 k(MFMU)8MEqTy+Tʞ-ar5yܕOXw!e;q-Jqܶ䓊Y:LC UE{/t>r"lI9)3KJjϤA 6SEE$d߇3KG*En|P\ԭTn6I-ƍKTj<1H_zwGr19wF N8ݝ+a9ɫM6mhePi%mmD! """"""*1bRKrD"vnrM۫mmĽm]ӡiG~e"˩ lhRTMk^MX["Jݱk7_ޕ*DqĒ&flՒ}`W}~SմZ{ĕ~wm*/{{ѹ_-0ط#P]xlڱ~Tn5wi*lڪ (JxioϏbqKYR|!|KN53 OS222$jzww%i}>N)E+rۥ7c$Ofl/LNث\6H9: FY󡈾I)fB֔JI_ ֣^: 9mY{66㒢7Uj]:.-os[R&gMF3˸#໹kmjq^8W"PΦURjʄWa˧T!͋ lW48JB2ko+ /Nw QwQzQ ے%$ޓ7^YL|r7!v%Trܥ &|M8~ybrn[RV gSn{{*#2#ԽᢏӴHak" ӌcwҜw&RJ07ױ>Ļ =^ BɆ)v32.M1=#6%̠tҤnzqMwԣ~s*%-j|_m*.Yx9Sz=)qE4 3pk+,`=kNRڥ=B=nŔNAx)Q$ԩȧ4z3t#Z2lҮYn$S%y- JzGpu|LBV7ZW#;Wwipܷ%(6jFG5#{$D"uۭ~]֫SrD܃fҎӾ+Tu>-ZTQ& N|$沸ii>eRWݳu'[O̻j8JۻEѩ[]vni= ڒ,[_%kC7I3Nv$4ɎЈeٸoUu:[}Do5|zNq=Tre%ɧ6&~DȍF]ƞG5q m]/w/ \ʲr8=oʔe9U(W"|S]uZd#?Se[W"ֿh][-7Nu:T=)R}.;ml*5Dlf $fF(̏T hiIUU4Szɕ t(%_|2 ~6eM;TƗK[f&]LK^CE2[ȏBOd;Mi|cx,^6;sیGpQ\NuJIFTJ~đArh* B"$H쉩eXPRj?sl"ԥ)su]xpԴY%VESH"ЋJǰ K&5^Ukzׄ8kEgS2h&Se\ Yl]WҶp-ZUvi7QS:4byqOo+[̺腋[6-_Fo.6[7$p&^ _GZԸߍkc.qqoI[9m߸YxOZЦ1uoiSH)P9Uʄjcq= S>֙NeR><;+ڌk%_qT].srNO?s[=vH[]RZHRMtᩗVؾ:/~u)ԍdg%=edVrISb{6vSu=(ܥ)mTv/J}̇8 S3ad:^hBSf؉OɔLhI_1d8,L><_A0y3rXq"'(۱;mFNII.v5_(^q~X>y{3צ I*Vܛv/jW' T'NR'j%ꔩ:mJ3SB}΋!-H-RJBТQoedi9tjENenPpke.%4]#{:>mkEɱdYWl\\\'nRM4&U>?Ќˉk÷!𴪛]]5}UqG~ݏI"O~s6(Ļ)qO~h}uԕd}Q~G,oE!&G&/]_H-O=o{k\̭bkv.Ô܈+;arZx)m?M\3lU$mk-CFXjTv6u' g:Vn_*qk:VC A%'4JV%EY)#BғO4<e׿jQQ]yUr4=wm[K1r׵%Iũ-O}|kC;/VcݩWZ)EHdžTru]8hgĵ-;=>U_ InvTm_jBM+QiF"9*{DI/iuo(=TzϖmPQl_v4z>T*ȴ>YF;ε\t]EH4ꌇ[VrLzef 2T^V>g2~kg5~Nק;{~Z~W}&ŒBӿS2$J?~(Yœ"˲ߩ\O]: J׉ښT{mmIѩn3˧)4LdFZ/zUG>U> n 5& ϴ-KJi2o]uKljvK3$bԔҚV旧iY5.ίfi96v7!v))FJM4{jG~Jt/lUE%pTAFe4qQk\ve۽/u/Im+W')v{\-E|Pms7߮DZRr۞/mu*1ՙaB܆ -xg3#6ۥtRogʌU)׎]ZҞNnŞr}F1Nnޞ;cZ{N}ۿMiuxʉ*3qi'9KHQ$WJxXyرŔe~[v5~/jN9Q4o6rJv FrdxM*iRjMzUinHdн7ᾞS=S'7 } ̽zt7K|_g J=Lq+/Bw_\ۧx\HJUPzQ<hqF[V0x==CsU7q|^ {)Iq38$_A(VgcKu06Ƅ"%i~_ˉk QCܣB8Ku/񋇵u([w}$F|8TՠI.E !;RJ^}MɒD_q2];Ɖ{5}*n7nEInO{Mwv}&q+v [V}Ĝ@%>#dXQ$f;iep.GquixVt x6bj͵mlKقQ[T]zs/&yەnM'W}!Fp_d^Tu N{ɻ'l{խ2.sTu{W^H&;1s)Pӛ6>$mě;Łnj= fLT)>׸+qReɴ[UR\L*P/!$Ӊ3Q 'K=m~6XqW3^W+ųO_[F$rR*u"T%@O +%# ]˽!aܽz{ͷvQh쩎]hGތ5ɇ*DzJDRNLi 4:{~2FmXY-zzĽ^f=]uū{/+&c:Ma{ĝDp2m܍kHș/(--m_vݮK(V{R}.k&yƴ7i^4@3f sK3^Ř˸B=]?gt5KbZB<e;kQLpxuWC}n 5ҴepB##~q= `x]KWF {GfŲ}?G.I9pjWkU]>={7q{kO/^I3==f1ɏ%nnʫ/Zu_yXN<57ۍ'vy/"8넭M2eԷ&Y,в33%IkjMr7xf nmQkX4踼>a-GcIeތw&U=-:qnW)z¥j :WqSZvԒ#j"KrIU)%qrmRoDGQ~SYRsu*V)  ,/x)MFD6O#]z 96[Ui(JRfw'y$GeUީkdMF-ݻ98F2d[o{Rn0n-xsV6Dh|Eb2E:KCOӪv4SJCr"J!!m,hRLD| ZYFm/X~ΧfrN&4Ƒ=Z9Mh.Mܵw/BdrܥniŪ8ɧ|y%œ[M=_tj?F!z5\evM:\ ~F-sg钬OWq“iiȍ<Gi%%n2rqͻllƑ)okw7}\Uk-:&fj솘XerV9yZuʼşdFC=rmo%~ZN78X(N)_7.Εn1MpJ}62jjJdI";R5&iLԸc:jmqiQj$ujp\{;v5B񥍪Xn Ą4qOERjzN(Ga٠䌡)p*v(J7#ZۻZ8O W uONb+^Qipv9GvֽƼϯrYƖKGJQDNPhRJjᡧC"21"9ѓS1;R_O7/WGz)8fE%F2ukmvSov/iZ&/]~KmI[:^~ͤ\kMi稜\ywJt3W7 8Ʒ~ݥeFgѼw"8VVSج\뻆}ݭ/J6Q)d|)zU3>k\L=;ow֯gN3pKѫ|wmkZ$z^2R:E)f>ς нd|#׆?\ǔpV{;\$ƵE%-ͪm0S6[n< kE[}mvE4DDZ^$OZ0*$~XUv҅B@^?]so#%ojw;Y#SxxueBگy v^i-)s)zV jC{7Gt.w3v,ygg8s]aE_,*E tY5k٨h=o"m泏:\6w噓aiL׎n^c\75AGkЯ0Lf46َ`egZ˓p/k;̛]kq!ݸzpԭG"}R9Ve>ˏHUjJ-&7nrnwG*Xv\˱/vN}O)ʼn&CV͍f̵]r\PMB-6Du-#RͰtRN^)mT _}nSȕC*_xBuTkJW[`ɩ`ejvsngP ڻ.-WUtܑqԹQj)t;vN&RNũT+8%IXӃ5fK՛-d9 ]CƑm|nZ-6=Hz,*aEm W3VzRšdY~Xf׀Xx"]s;)5u*ُHB BRGS6bݶؿ 9j[1*jױga7oX CUI%0v#~\-O-Ꙛuɷ쏪&5mY٦M`LJ2qK~HZbr =N'YobI. (^ ׾{_ ?OJ`S`3BN[}5w6:ǵ/iSlt=4F*d&T4y/#. ɵim5Uֲf 眕6Y7 fơ=3dϕq뚩$qTM-%r!$@A? ޾V0c~{[{;򥧅a~ڵ»&ڄv1ek=wb MLkNAԬw-x>~/r=e73VeVN)K%Sښe"+3uXuچrn ֺVzscJ峻m}vb㶓n\YbIUBT%*,0nov=;z꣓S/nSXSpl##k9mXGrZv^Gde!ŷRԠzQyjC]`gToPov{j~KRBMY}i[߶9KL2ԉO0K#m>wB[ٍ+n[[b٦DX ݲpo] [\m5qdT()mo4Oy9Ie b][wղmM~vmi۱~t \}$яimRk(L c Cvk7r9_r1 ;zv|F@KyZ[&jEji/"6$69ml#e]9s\{ScL}Ȣؿ0q/nZ*t,CLoD߉Njǚy=Pgmu6^]l-["çUʖMlʍp-"qmU>۷uFOJ%Ǔkx 'g=睋k[3u,{³WɘݪF]ՍeFX"Oy\,cچ=w/gn Ļ]#2? vqy-gXnR.^}ݺFs{ŝG]}e|#0mjx"ƬWكm?rgU^xVB":Dt>@LRbun~ݭ,w+v⪕;\U(RYa61>#Jm˞Μ9g9XKaG='u8gf}'qy#ɉw J]We.ʲ-<+&q%s?2dњztҼn`cΤmmqMdz O[-ߩӲ&;[tmܝVnr">{x<8U+p:Ig]zjGkt,uzf}dؠoJaکqEq -(:d<պ=eKy[˗^%ZXkX[C2߱\ITTLGzANM￵i]K>UsOGDDD.ZF6* ҃V Zhz{'xp^`wo8r0h ZmJ5"jb[l=yUu7-;7IT%:jFjߖm0tzU'K)څNۧYJ)4IQ}^KWm7kSP>q;ނ#)'n7&׊r?óM{IwR\j2Qn[v pe#/tAF\ϵ225q֒om6z})6҅*oqDsMf CNIN=T S2t,_ѧ}kveMF0J\Rnnݙܹy[rUc-j{yGtkQ%s]5qB.Nw.JN1LvR Ui5J ZESQԙr):MJ+g}χ!2;q([jAud][ljVK3$ײSJI=/|&tl'*n۽f.frܥ jQO8>&Z];.|7T/C}$ڋUmP2Reҭ8hFF\L 3~e v\۫]ݝNmrnB%*]Z«hKc=BTLG :V74$=Ǘy+EX'4tn(I:Ѝ;Df8c,k1%dJ6.j6ź{N~l6&*fœI7 WAlGOu-ҢH,,(ǔe뿋쩨kM܍ZſgRvQ' 9)?n|er˭|I|-fGK.rΛp8XV1%K6mvG+tc+qE&ǸC_Nm:l=_/m5^[dߌڇ.c<%:)tQ$Ow~-aY;UJ>=F)2[nk؆?훐M=l6[4(O.]2#-H^n#->&mp5~Fӛ+|| S,xag%qkEUzUgæBhߕP(7]kFnq?֖CpruZ6*rEڊtS|*tI*E}7R<,nUU֫^I7Q*mSly%rdȓd8hE<9oHhMfNSRj[i7D[Rj݊+kდq{"$$H?p\̅S?㭻;t~R߁)^/>Qj`yt[w ԛ;²~+ߔ_ YW~|o]?x^ᯛ `ʼn;g)T@vWn]>&4lp+$D̢1l|ȨF%-}.9[}w~ ԠLM9hСablfe&QoW!s?wjLK?s7yO>(=C~_nyǜu?v3vyo oI@qV-jeES^[9WoSܝh"l2C1a͔CiJ@3:Pճw=/7ovuk+\V;lDgն<[A+rX~d;m!_s8ݖ׷;;.0llUC+?i#_crʙ1~C.\–q ul8Hܶ2m`ܻM3Tov|Bs rɵ"oLS- DКw=Tv@f'6|YlD͓Y%׵-#Ѯo%:&!3o%\J<02;K87>^vgƓ# ;ݝmz^Y6=PS39U%~ &f# }o!muH;ʲŇ˷yvP+&.7e[3'vR4Yj̗IZ`e˽3o[WU{ m[sUbۋZǾۆl6~9'V*.\S2<Sd*zY[aŶ`]C$n.v^Ʌ dng>ەZ,Mmϑ :n6nϦezWqUJ4! ۇ4R! =>>Fn|Q[{pRO17ƕ~._I''00k=b՛o}Osðc2'o\3}ݭQ^2 . R1yKȣtAݿ-uܾw!`?1Whn|gzUo[ECWwjUIן)^h#1ɭ!/Z np;o;ΗŻkXs."6E`Z1 עӐ9Kl8qd q} 2Stt;#j>;խabONŗ=fwP1j)l6J̶|gV2`y/0E˛6+ԫ1? 6}KW c\KoKͨ2ۅFw–s*TԞLיuDx .kCzWXhy۶gLu|%TnupǺl-S* PRaLnT+c+*xl.v!.U=|; !_L̎뱚U=4hm:ٯ"y)$:>%(n}X'p[ȴ ^˒4kƓmzDx \ 'NqamP7nyN݅=j7%McSڵj%STy qXymvCg{w/w=wSW5r̹u erծˊsOm=DhEҚRb#n)QOxtվQwe]I}wCa'"[ۂ-z}2UuKP$㜉ԧ:mc<Ý>RoL?wu|%ҷ&K y_!y9 ??:tq3(UU-lkS'ɸ@jdzQˬR] EVPW1DJq2n:,c|ǻ̑;y{X,ۂ.u.b˕u.tKBjQ"[S園S`ٮdNبeJ&9Ơ ~0a(Vm٘L+Jr*vڑE( x0+tp˕ n';wm-ޜMOxX>{#2%jgb2M[`K*\5@8l'e=0u+w ֘鳾{y܀:R*Ya]"Ӧ%ktynlۣ65,3gU}{GYrb;ge'TKwǘ.,rpܚV]Tr,!dp /ԺU,xՉ>s׽~W5oTh yx?xrrx?)?ilbT׬,z$Ԏ.UH٠\U1pU:]JwSrGZq8àd驐,N67QYBӢD㏙W!Q25ϸo9ms-7-%3CihO.J鯽-;MZM8ku-7k9S$8]q2E(}bۏI[DKOK}3KUB^u %Y,u.-&f#]'܆o$x`Yu,dzwM;#oKxn;\[d7}Rb+*Y䛂ZuBӱl{j0O̓}LhK;[aֶaGL{Cb#S.T[>߃F]NK"u^LUʐ_ykW?!GRj29͖qa'0[npcDvV)qz9R)PۨM^aJx W] r>];eN3vxdmĘ(5W2K1䪖weF{mE/QP6\u54x5[hۮ-Nk”i[lUgL]J}5 S:EhiUrgHl!ŒJ$pe=q^b͵Q' ?6|R\,JA ڵ"TDꈭ:ymg`B5t%M] <N_zv2_Ortٵ/i/ReӮ*7[qүqEG* m"[I:6e^p"I$jԴęh!m)]GZkcjS!{e^z}+Cѥ9;R|/ֱeiUԏCNu2Zhcٗg$ݭwvr P8*7/Lk~I'Km1+MW%Bk|oOm>-#qj*|Dbѱkn|n{v#jĮqNpMIUm(7Liz;{ҜݞڝVƚVϬ+sO!OstGvxӉ']uӎ4g_ 1^-8ۦ k!)Ύ5O;YSB#2Zzχ;<.ֵOtge~.(RC#wFZeGZٸ6FFJ4e2ˇpJT$[wgV)q6muDGJ56q\I!̗ y/I~RtJ9kJ]Iy*'FN0s.[l!fw'y(7$œ WƫgyΙdMEU JQJv̋vmrۖ.jWR_M֨djYgSj0^\y'EoECjm$ IƩK>Z28J2TiJ2N#}.s cArl嫶nB.FIJ.)۔\ZiM>/hLĸ=C1s[?YMqp|94- 鮝𦔽/k^#NT(Y LS$6˩}{;5 )B۷W$qpN)qqoot}ZDVә;7TiK|6f3h$dԄ}fqݡ>Nb򗉉+ͶO]>ߡ_VtYf79ڰիF sq~prս|QM)g%l0ocJȨHz V;Bb/kLAcfPJ,ԭ{ƍgpjNR6VSI*$!yV足jᇑ.](EܣqM\qJ2eZT).<9UB/(B0j)mtKEj#׿fDI-=rZړj|'Nڤ]k*i$5qt"ݙPM6E4ke^Z8ۏhz$Q(R Ay2zfRñnpnkbkI:=j &ΝșW?׵d{+ύM'??XqeeĽ.[o=UxFS=ӷdZwenՄ]_X=ĭVa* pKs0ބۍfJ3 gz̚i|wnxtjc¼5${(1fXQ65ȼb̶Zkn>%FQMJXӡ{TZEVNᖣimT/37cNJUPnP҂ZOE~"-Rc4^b- FEͧtf5[)S!OZIښݲ͑;tvܡ+N)AR=hCNn;wL16-:特7M$=Tҕ-.R[HٷnXk sn[ҞD-0WS9p9:-Ϸ-jѬNu{ҹfv)[Ľvwfg(ٷfe+0mYj8Q1\ݧg]Eǎvڿc!4#j5̋C2"}BRriFp7=ô\TZ:\BLfj#I22װ<;صZl j 6:l"6]۸ K'6RTѯ^ئOԓV\?$x7s#r:Oh{ց=MmuHԷd{pN /܅:UE#Yy+(SgQ(Щ)RHzw>^Ѿݻ>mK&^ '$Jۻ&w%F|xfz%˳ L~3N?Cy9 v w/{ƿ kz3x> sXv}vP"@WyC z`'톽Dw%-tt yVY\wmuPYQA0iG-2JP,6/gˢ]u.-n!Zw.N7Q]Df}Q0({a\@=i_X7gFǘ8^⻲}G MZ1)WEfO12G+=-B@z\`||w6ċj߬m}UwRox֢I &c~XGP6Qndpvܻul'V7^FJt^{b^B(L~sѣ6@߿^xqU!ڙ5|Vpvef-uӥ^3  FSDɯKD%0r}FF穛r7 +o"V8tv̖NQU!5uFd"bCr^bJ=֤fM#ʳԷP0O-9xRBm\=`r-:;~3Tl(nXtXi%2Vٛ#vwqƴ`L@"H‹qW.j,JM5B[)WܺUeZFqc'V˷1W7V̾-MHФwn8N;HPSdݷC7&2j.W\τGŎ'Vb]c.x+Rx1%C2T{myg[qU|+m:M:շ8҉yWd)ՋWS%%:iqlʹmGwݹ WnNŤѩ5(9hTٵDdGUi-)vSs2 2{OnT$Xck n:¶(lASLeȔBjμPpTb2~N2~%^k[ܗ[Jzs0ӓHBKq[}JَA-$dFQgjxxFv4r/x*Rm% `4J(&iv7SkԲmSH1YWmx 8n.k']:Z˭_W >ڃXЩ. jTq%Aā[E}amc]D:rmHRiu:uӚӢ\p(5-q%e)(۬ҖȽIf<߽pr&ݫVfY91q2ĭEQgYbTGQ&,yL+N$[q*RVۉQ=FuTܻ>f>f㋳8N6$܌n)9&»iˤsX,݅܍ȩv+sRTpO}d?Wn/Inpȸ%O]StQO|v5\}7Zwb.AIVK^:wb{[uݯcytO߶S<{8KSRׁH̏N7ۚ[xkwYy_'ZӵF+>쌛ZUĦreE9F[24De{}@:ExWs-\ǻ7K-\JNvEk%:s˙#κ].oͳ;լ7wB6nwu:$L; DkI#Wz.:Xp(˅v$Sq,wn\qIN-e<5Oe+vuYTpcojUI_ާP8 O 7&VL8z$_B-H-[uh]T{|8=qVRN-:Ij:7PUtXϷmy鉿:RIM~33ӸS2#׳GdŲ5+/Bx{(WzȨ5Y㞎#|˖+ ط.|e<o/rߔX>7s}VE.OVti׽ .5nNJO"95{#q}Ay9do]R"M6z\tnNS-D!@3N_jicWsy*5uٮRcWv/.,j}=S)j5C^> Ie =gu9ӛqjtz]۪TMoߧI!Ǧ¶m:,"[L!{qAv-o 3{"KʼnrIkfٶj2ƙ؄S`7` k6jzޞ?e5G&6uʷ2%ԒRKE*G\Npom F/V |C0.q_eenƣ<5Oh'67ɪn[SĽ{ڔjǘzs;~׌(ۂ`ܢ1ƣ` _l9Va6%UQWh~P~\F^ZHR@:ۧCJ{ôGeBh;~ۧnU J\O+n2 RҠ)ng}Kh{5+S×ܛ.1ZjG)iRȤIN 4%{oΜ/eO[Nffd ĹK?nnԼMqX'܌nZvq<ķbFnͪaQ`5 s,M_լ?-@_{w{ӺձJ}GF[%v\5[ŒGkOw/ΜM9rjË%2+rd~+󲕛C9U۳r[aJǭm|˒LAʨSCq[XMۺoubfp:t+ΤĻo ][ zt-*67kvS7D·MMCQXm;)܎n_h%]4ܙnRk!]ڵsDUF"`R, &#R_*[z*ZqFXɻ]7|۵w+'pFDەs=r./ᐚm3Hשy yD"jHCr':sA65نѮ^o1V/ f;nFr3VM)e*- s D'H݅fӧ\*޷[k<7u<-]֍Q8R h|p=WlW3s%Q %3l}@U-K6f-NϿu|ڴmWN׮[׸F*mW\%r! C78:޳vBG7ŵ.JթԚ2x)ST!řn~9 W:Wpܢ件{xf8ٳwKE ҰWxVB\qBZ 2wMb[lGSnyԚ~z9ZmያvoN2Afnݽjf>)j3 !;gOYʹK" Wftڎ+׭b*2ϻK>ۢӱeyԪXISUm[z+ugX%0lϏnvg!;t{BqPj>PyvR7Cj]O%+ݲ :qiMj6W}3vC/R=4Som]ŗ=ю, TF6U_-\6MyskwMr&Q\wjKܩyMϣUj0*}RZܷSdY3>Zjqj6TgzpA/M`/Cmл,޻feE[/+uk^Vs1W$G(JsW2ٰu*߻q*Y޵.Wi:ur5T),=0uRmho.twܖiYwrWHntvEj8qhf`Ͻpf(R&>Ki%I7$QӖm-2 ~yߗQ-앑/ x[k8nw.c㩵k}]FkbJl:{.(˩n0Hqvαp7 귎.Gupx[N`Yq'+ruU7[ү+>!xrȫoSo]OC# d^Q]\>!ƛGw^Mx"-+%vdX-:M2UR%d>%l ioSu6lsj7D P>XxHz Ukà(n^Q V>5cVtWj SEiJdznyej[lE' 3kuٌNn4JW)gB {4 j6&]' m-(ZMEz8cz>WZ6#7+[,MR-Z!4ܓtCyE|umj1ƽvƷV\;%>Q :#Le(iVz5 4ũۤUWxX ^(ҔsլB2w-V ^R+; ˂M\z+Uwr+RWY⺧~ Q*JcYSNSλUd8in=v K낫k\IRרSUaCFmϿ5̗P|u ZTԕ}>oYѲ1sfP+sQkX8Gb~6r,s>^\,mGL+7[n-E\.Fqḕcl*Jmjb5 ,m]c}NXfeVlǸJ5eˡ$4%g~N p4Y*WwW٧<8v#;qԩTut,m"#Y D\5V`\\Lȋ];LȇiS6ϝZ l>LruR\v=ǘϔDg=ԈdFZ+M{=|,[;0>RiSi4,S5}yxw&(E7&fݙ4UՕ! ~'Id)]ǽu2K-fޭ \08Vڅ쓬=Vy^^ IhyKR-B#Ըr=]mܻӾ'*Umkoy rTqT_i,/8Q^<ݤ|4ԻO(܄"'5N~#m.(Ҿ2i6Uev&I*<}҄$eNtÛzyWJubW^iBW.܅Wڮg]irO6Ve90sgv.+sV޿aޔ[p?3q*FutUo*eL\KM'EG*ZcAFfG5J 5jj=MJ3OK:k˝'NMB7m3uFҕ\-Ywg%PRqMIyZGY9|μvn߻5cWݷa^+X֥vnݘ\v7m>Fgzv"-;Ew֝}1|RjN𿊀7g#֟*GQQ|#/bo]p$>_Un9гUbn9׃ErQBU-^vDmVh'<R[fdHT]*~}3j;nvjc7s-rӳ Y8[n[1pJx kX[Jk9Mn!_Nю6x:iZ˦U |߉^Ԛ݃hYxk &U^bwKk.[jE+P(˞=9j@snCv7%c_7=xǁ<l {t'酚+1F‹l׭:ݻILruǶkL-L(K0L1&>wXB(pm;1fpnlp֓%Skidkt(U +xulo'/ڕeN r=^pZZ:Pnj8Hf"48ijY[ N[yZٻ+=  ø:3 ?^ܷ^Sr#YK[UF?CuhC b]GM')mڏsNrܗI]ljq6VB. W,UK"YX5{c >Iqā> T:n!,5l2VzCl|+I[*SrjnS6٨y+x,@>П.g+!rn9>N|W>OZT_ut Y""v7|sfި;Pclm EùN,{'fNT%U&LfH8~1v>Il}统u6P˗c(WV~H^bMU.o*oOF0N:_:6Smr_.b+|ݶYY غF,mwjv>f*>QM뭱Sd:`N{l/⎱;n-z~"Gze퇎J5S KG9!Gn;N1 ݎ h6m|S?ɂ5'WOÞ 7|7^ao @mxGmi^jϽ>01Mf0լD3-2T. VXR"ɥV Kl J O7|u?bvа;6.eߓ|[1bmRr,eRz`z 6܎-ͨku͹Fː dPhYgZUj}nvX;z=gVեTv_J }\1n7w2J?ޘγc\E 1Aޑzq;\r]]\Y&[nsNei\uURje*Qk2CSl*xJz-xٶlm+|UjUؓ`Ladqiĩ!Gd\W~fz;Tn*PdRM&T4`չSWq5k훶(N"Ӎ% V]֦wb.nUO!u*J&Oӕ2e|Z=eV쫚΅g#+/RW:طnbi*Wyo)p{:ETKؚR(RY+r웓r(IF) VmȵNB:h Q1ғ|u8E]{,'$-TR[j49l*3"I鯴zhd>Q+\BkNF=.$ZR4Nwհ(IpNi.(Gi33#33e$FXK*NdWrud[r{xnk$v2ıh+J1TQ[#JQl[tRO]LHKٮ NӍnF񨔤֞Em'MILB"ԋ%dBŋ+p̿_17jzT~4pc Vo\ƹb9Rq-'1j;8ܗ)hE%DZKS<璸Bu*%*Yw5ڻ9ۣ^z4U; Ñk\U(o~G?VUĎ:?P?_F_Kߤ~ᓾI |pr.Ok\SklRhҪz{­P .}SktZ7UQ4ڌIM8̈eaӊJZ%FFZu,KZvln廐SNFIVtuNi?CM5]+Ph,{jN JSR$IS^tSUVrORYu.9WyP6 [Kiu m!X|]Y79ӄ)\ģ)pbڳr%*&ꑶ_-H*dzk)1 V3')UAϹٶWRxe'պn۫h7AR9 EAJeGLms!%D| A 5]/Q3eb̄vnVn%za\m kZnv([emqrIҕij|""><hjJשvvǕ|Pޟs}V~2&Z?+2N&Z4w@)4iSڪ_>/JN9Hiۏuf8'It[ȲR.hZ$ȋ_Y ~U<UUO*6b)Ovzڜj\R̋.$FsQuҊj^נ䈈y<zZIuP[}Qm=C?zN(Exqu/kn S-FzKZzOסӽjJ\)F3b!r5ٝ|;6 o=-3*λ]αb\abqRi-w޵⦪~b8Kpo)Z=>)ғ"5/GTZLE-輵f7ݘ۹~+&+w/7GFI:l33fg.N~۲\2|*cnermnnM+Fq"ѪIz%j =YW8@~gc/~?N'?)«qȸs➟n=k" X“m֮VreMh2[uݖ] *FܖN)MȐ`f0 g,C9̑o;ddudJ=In13:ݒvvdMUEJLp^,6t-@͐9'{7m{-3,>hnF;ѰM)->>+Ěz!R* :`e--m7nB\u{b U>[8֪]6^ߤLʦ\DFNo$$dͶlgno8OrsQ\l̯hRo8tuNo+ CTxu!2[>ctFpeޓƻֶR"3QrQuOѳgwQr;S~)6HhZw/GgVTmUf_yt7%$];zLWF̰xy2Ʉu!MCmš_0[W6jf#a-KLi+3Q7c^qg%s<1aYIQeZf+}>;S6L0]Yu_h9߻<ƅpmiM$AVvŚ,*#t2.8Y)-Zhshü97/#Oro"u^/uFgWɺ,p:6a,^x%$Yve^3PƗMnTP&yS}OJ '덫MH^:rXԴJۋ/rI;S*,+yz1hv)Qw^ڍJ2oL׊q(\fDj:^T%vOadɂnS}ZO)N*λdaȜkG_PIEO}нa(^iQX᯦-7^)%g'SJx(.S9zVɴZ{E ))ۅi/s7 VIV-|sj0*UBTHIqRf>FP$KqN0 R̻8j\GcC}IUz\i 6F)Q{Gҧ3qSzKj-Az VЛS-zy:8*mNk|D鿓ND2u+0Yŝ7kqm·?8Ib]u>˗^_>(]vӋzv+ݩ){vZrJ2RQ몋C$z [,pp,8mڊbR]Il .f~d/ݓs㓓mͶ{mgjQwn=Oic9ܚm4Q/6ݨ[TƧ?nԶoytf{@AzT{e{[O'ZRZt~AGD?s3􌿂ՉIw'|~U\ w~di:Kޱ)U/sU%njѩ&GSP^ǝd)..!^U` 1wX[aԇSxoFV6_扐)T 2Mfd=ۖͭiZ7KK Bi9%7@<3<ճԻU,},a}FRqɛr i@ONJvK KLN M, ʖv0n-]DwlI-X6ܶ$Jʴh5O+mOI+Ra瞠\ MG7BفjYo1#͖0V`Ѱ2M?c8>-Crt*JkIGS:e#hPKx[鱼>{5m;wcն&>j-M֥^َ) 6yȜl_w{-ō̱r> U=]iw3)r*]:K]6BdCTZ|>gf}LW}[$'Y5 &c -j.z6R 67MԷFMnÌwI7w5E}o޽+K ֵy4܌ȥW"COyR[q5Ӱ͙f[v"_#q{MV6܍3"u9BK(41ӯqˇc${ߝCi6I(OmθzҜ5k^:>Jzw.>qV8{vU[ڶEm|DžBz].KHjI]x;Mɗ{m,qZXr忇2u^RO2Z}ZێS[2Jen!*NDcrBUً4<ǼMҲs1Zw57c3&ĖڻzmP*FuJG1-dN:|OU}ҵgi2t~F^^Z.VxjvŧnNNh<:]^~NN+ge^g.SԔGFe߯'[vn'(ScJ]kܗ7eJOlRrfziݮq̋S"\*U<*W]k$FջV}? 7g#֟*GQQ|#/bo]p$>_Un9;l S VvQU%OLU{οmU6bZ1MTx%!֙Q7, J=!3 ;Q,ڌ;6ͱ݅q^&ߔ·n #WbwӖX.HtG)N&d̵zpI,n cu ޖUj+VXUp[w]N o.J6Z8Ts&utxln;~HPHS/xw`G\ʡ¿rj Z^vt"[L:SD\h0sUwR,}[x^X,R2Vn< ]2YDr[SRKs8tXb̷G?Ps Tv 3be,zVz D[/I.KOEQrm'$7|[J>r S`5յwT#\w1FTz\Ԛ &"ׅhSHrD\'r]~/>p;:Piuu:"9ő=tTaS7V2rӷk7mb[^WmPp*[y.Þ6f]cizJCgRR@UVl큝.WJP1N{/\whZ ػϧӱE7|E֫Sί.x-Y&pi%v''-x6r'Ws*6=DwwUu]=C?MK [yrtܒG$!WGqJ*%SAz ED[^)/tė/g=#Omd.|^n/sl׉g DZqemqowݮRzUܜ=ڽ-o/Iۖ;qVʘgPp|mm;6zGl9.8pwWgsJ2qPbe}}UpNjٯ}7TMQKrؽtEx%v w߾8%|j;~|}pK]ơ/ w߾8%|j;~|}pK]ơ/ w&~e_H 8PL7:%ʭ5Kw&U2vwR_+rm'}C7#rWoO&HoG?M$UR7{FU]u ;# !Wk`|W>׹潇9Vn)6)*ҹ{%qV4q>W1vi#T"Qk&GwxcJBJ- Ϸ^ˁxkU}ԣ/3.;]J=<*)cS)ROK9H=,r zX @)cS)Da^ԽQ gxJI=w֣gf*TRj

2 Department of Mechanical Engineering Education, Chungnam National University JFIFddDuckydqhttp://ns.adobe.com/xap/1.0/ Adobed     ! 1AQa"q 2#w8B36v7XRr$9bCt%u&Ws'(xy4T5fH  !1AQaq"2B Rbr#u67Ѳ3sTt5v8Sc$4ĂCÔ%UӅFV ?_Aנj- H>>,m*>fzp"TrKkr^r.|_&]|*vPuܶvoQ1mwVJUhu-I"=LniAƕ8"۲ k*ҿ[yu:.vUQ+)%F DHyVBk>Hy8jݹ q~9D4KRmzQ)^ʔ.J%k_tVi5NTjg!'ky|5asOȻ)R۸ߩFMԿ3L4j6dڜ#NIwUF]JqB/(FafJRzq3\G՛ ?~\ 6)6W4m[O^L0E&rRMض*C .]Unl-1 1r#Rj/&QɈ׉˩s6Rj=5Tg.y.·Pӡ:JJS:C8-2u]d&vUz;7p9 5VnL֢"y)">iי(IDDd| Yj0; LRfS:ktYK%*N2^m|&dğth":ey)uPQZW)gcC3Pv&MMWd&Ŵ۲mvTRoժM03*F3Yd6\8,\hݻ kߔi<k NTwSԪmljj[>->ptU%'LR>&EBH$MQAUx[$Z6vi&_a.KIQ{hyƒ j"JOC9eFҝfj;˚Ω<[3_m% lQ@4g=5$(J]Yc-OMq<Ǎ wSzڗ)k$7VIP붾ͯnV+卵*t]iЎD31~SA1éC2u)ʼnQn-Uoi3:grI8ؓWm*G zܕ)ZקJ}Y YlGeJ6cB2I NS3Q>k=KTBT]W6+SOXQgGR? telˊ%-Re\hѯ2TF"C/OJΩ6r[N.0{SpljjX1“jOsӥ;ҭhe}xu`Ք&.)yO̒ Fߑ.$Qw;9Iw2o+RVJMSOj[SoҌZ%;`d$blQ{Ro{Imڌ>3egf\O֝Uzx"䢸g+mv%Gʆ:|V[N'&ס-ޝ'kfE|K,G&˳98Juin/\\Qݿ̋v~Ǩ!rtWU d|E߫R4d}.qPw*Ӭv5YEcn~f5c%MTMkb-F>5JT,})QHg%{("ӔȸWMsYyWNRrkkJr0XドnͫT}r-jj,Ŕʍ\Q2Ri>v$5!]"JB2WɅ)]VԜUc8i|.jeRO6^V.¸ Q&#|ܶ-*uOG%JAtRZRr]FFG\۩w+?'zչSѧt jz>KW&ot{7P&2D;&\\>Q2JzܗAKSfeNn[jRrԕf6,q,F1tRfԗ>vֶևj-&R'Zi2=xv~Elbsvm8=ӛ"ū񕜈BȩlWau[]ٷBߨF~J!|Ipr3R̴#Yp)={7:G{+:\W}n|Q#%)7^-h"Ƒq:M*%J&$T軨I333׎g_- ucBwwjp[6i25$̏bU’ٱRv?G\~#Iͪb7<<}Ezt" q_Inw,7-d,G÷%T* Wg1"䥱kq/A.,_KhqŒxwvo u2ۥۧ.bQ}XκA$֣ +K״ZUNmڸII{.v{5z5ѮRme[moyƾd~cRݾK'j.\i&/S6f|b=5: p!6i_ 4j6=.si˧eƾtS^c.Y^RJVS-Vi3,esi08?H$GvZgg?gi䤟2adw릿:"۪lkSN>q-4kI܋ێe̊qۅgDoѨ9; #T.Q;7#~_Ufstb_'w~Xw1Xk,vcOt._}v}8"(4Z\ۘgk?J?bm_c!g{HZV]Fkk%~gEt)b秴vΰB|꽸}mp~E6ݹv;7P٤v+ri*3Ԣ|'O14_~7nP{7ZU\Vű[ +7󖱅o#:ǥŬ\|3r%TJX]V7ez¨Y]lc|O3V! R zbJ'PnGqVJ"19WVeOF埜EaEJωqCN5Z g-9[S<$sUK5b|7sn\7x qmv##FF\ w[=-43$^ooVSiXօv7iB۴yg>]Vf"r$J3""32!Zh[K%7GvNLs+4nB/B{vlsobJaҺJR:0g%&zR\ S3T[&ִor*ⷳc3ʊO[iozW٨%$gn:ܶWwFBԹjHP&z u&F2\f;ipW73 [; '_̽b;vib!oec dC-tS__$Xs]l9&z$2/N>%'[}b{h/{`{Ji׉׏ YJB/X%}.|+{(S:qz]4_Kѵo`^tY_4S#* ^zvݾMr+TrkQ g.8Ͽ^i>ӈǙvix>$o( ^qt*&t1oJVu-ql5U6jCЉmĻ*"?JT=K'O/|=Vo}l0b}}f?X[?/\JSBe,kP8ETJ==?.p5ފgbU9}ǶdNKk—_$8̸͓ۍ8Di\BԿ-1v{FF]|.^ۅ{vl12׏z7-R7wE?\nh\jN/Kձr_oBw"N QMBZqe-m:ӨSn6j4%!hQ;sv'm4kcM=!8\m[M4{SMliۇ%eֽR&N:{2A8)THLK3Zj[jPBx#BگMf:G1\`edcʮ?|w(-̮vXt,bW2;.ιNHRR#YwTM"<;mk\.foIDjmlJ;vxy7o7i\,KQŊ9d^Mmgc L*.T6tLeIuOH3SJQ3=F/ʿ<9\JM6mN6=<{xkP!F1QR[I$6ُimXu2An2yԒMU q f[IB-'䤯jYm52&JG\zд\~vdg QtHGXw&1Lw+nDEdC1w|YJmvP)HZ>i0BPβә?R:QO["]I_Jʏۍ>QKyu^bycBq4lXF~l [\*N>-J6,Gq(Zr5h]CwYӤU~ʶߑ u*SIv%ZfJ7)! FS*s_\|IŸZ)J ]ܜi4"z[+Z,MOZ))}|Ʀ(RUNIII.S'ˍO~˨rn}M)xxӕ0 eyҵ7YMAB]ӣU:/ѭ*6bcwP͵ "+qēVjŹO|GtY4V j[mLV M -m>",B$ GD1~j6O4|LxnNmqATNR3ε|DŽa[fmn-ڭ+FiK7Pcm;r5 l8r{#-]'nrFh2ruycb;pW=njRqRJ(d mnpckNnʹ+6]tz~E=ʕ l ZZ5jSi3#47.Lcfe`9؏v囜.F\-UZ:*0_<Νu9Lӵm&)_3\^ҹ3"1n1v_|uRʞͫr'iȧN_kH׺8xXrj=\МH)V\ˬ.Xʸ oVRC}ySU9/OBY먌5 ٿwޞ)rw8Ӫi5*5ZΗcGƱ !ZۄlmpjJ -l <R̵/JAպZuq\IdUS 48wXJJtcg4cI~aqߓwŷrm-v)G7yS^7H^-\mŌAq|"m9IBnF㏉9[N+mmy/!KKۉ%n +BdddfFF6FQRN-U5;Sv'm4kcM=Mn)\qιqUd9F%",6MGdT%-+~ f%+y֛^3SrF>6lc(֪vۊN;g._0Sѧ]ETWرkQKzGe9ʨsKA"yC y2\[5 rԭ7Gk5Mzw_4sM3hxЊ'oÍ5jsub )ͪ~tR2H]R͍>̋m6=%(˿(Wrr-܅y5(ܔJ޺YunW̹븹NsqK ]/QR#"ZMDfD|43Qw|._ԡSqTZBg??O Ϥ)/E_U|i}2 9Z?¹0:x'3,whǣ?C y-A~=daJј&M?D1_PS+Oi&;a @;Dž7[ zZC"bv:jjMQk$M RԸ3uA\=wI.AwC"^.{?-\NSiˏ"b}T/}q/ o.1M}R%:-ZniʒL$SgrBW*,Mw'N\ɇ{s\j]VryG'8f`}'N<*/`U숻z CwHq18J+vԕKss4R53/&XTt1bZƟo\=%nO)h$rBi-nKĪ^ ջڜlwkYm[̑+/QrZo%TQ;TLs($2C:s.%+eoNttq۰kK7O0m_t_pZ1SsSM7"mevFZ[w -FJ*T*jФQRg BSu|]g:ɵzjqwmltL.e3sRMچkSmjkmWœިm++¦'tILk*բQ D,PB\lI[9{%Gb R6öۍmX-MaʉA931cs..G4CujQտ[9 }G-xwl)IQz j Ó"rqe&=]꾧֎c)<kӳ+0JrRR3'TnXi^xMF Bު*tIL.[h"2"nKzZe'ZV/RrNYz]8죝n]Ķܩ>^Ժ]u-7^\mZjܣ9+Rmn ߑv?oꋘ?&ƪy^N4o=3-ؔ̿*`}V݁ ƒPu8%$ ݗ]wt;\y\>='OjPIp/nJU8{϶FNMsf"ίNqƹ(+ ݮF2Km |jܴZs%zf*eȫ?]4)I۵nR&FX + [jDh(#哑9q9Eծj8noǕZf\J-l&Z˫}`ӎhyrΉn\űn]9pʌӣ"׮Wt?N4_I_~54#/my1Xr*척aS#DT >q ssΛW;3oUaJSRMDgQnt:Ql,/ ܷfRqiM Ȼ>Cob;A>ڦWقM9X~/!'MW.}Vrߔꔵ!5|iB(0-zF=}okڢE$^wW~nokY߮\6՜̌{i-AF*9)\t9IV6۸5ZUF6R$ŨQIq砳YUZ]eyv >hI櫥N )&l JulwE1GDOuFN2| }馥uC1rޫV+^gdb&W[4<^e4YW,d|htͮsUM)۸8:{3d{AѢ)~ \#J=NdƮꮓ90 |1K$v*?мS ]i$J,C,SG?/_՜pMSƯM|mG1V1$~K>CSvkuj=&) -,yLjuFHK{c駗.SOua;BrSqj-ۍZ#'Jys7[g2z/.u4+XV2VQ.ޕ)$"(%)#Z7suZ%j }BǬݕe)Jvz8zJf:hIN|svO1O#IEcۍjݽ:SdὮvu^@:o^5cs>i/VqmVm]ؔܢn6'vޑ̗J4Wn@OlKbX ;n:hgJ9ŻyǑz8f܌q&Y fN0N;[69 rbׅC2/#kE l&2~èMR.*%g=Ft.%؝e8<.e=Uv{~㻏"EˑnvDѭ͜Lu3u0:U֝$[M5<:oi+V4V9 6nXvx&_ q Qqw3W:uϔ2yb/(ɳ|5zQiJ#r|Hw#.W?4aDŲ\ugWG;Cw鐢K|xg)##=O.dF˟jMUvWĻsr.z]kPc9"]R)mkfOd*uYf١RsB Aîh=k]ʳUrrZsq`d#r$/Ը3o^&lRWȍyuW̦Y4QDUMJ65ƒ[+ygk XK_±k#y:8(TJOSQhJt2.DR}"5[) r)6V6u5k:eXZmv𭤔!푊Q[qQ}ҹLE- 8qIZG|UM4j}Mܕ[Vwm{} Naqµ"ԈM zOpKѰ?IAD3Ir0'/q1itoB5{%wkOBn-ۜduqIzYK60{+DʕܞqIt";r1mG/\/ym[6JƫR \L=S=OT@Ix[TMm{>ݾտ֒ݸӉLYIx>+"JVNzx||5rI?C{oz8۹e\R-^\A2F R+N9 vlT]"ۭ d)t֞i #E2jB@׵=#/N+!ĕhx}I!cM`ąZ*ŻɄҒ߮Y.Z}='/oۙ3IpW̮hT7cTSuz9>B}΄&h!>lӵn~j˅IvU.'v'CSZw8QK3G> ,J59ٷ+HSg䧎hJdzvwv-cvxS5[̊n~ؿ%ַX?O0\6ne 6kn9.ϯ} *h 8_QhLݣ7q +=XBҲ5?[[)+F`=4 }B,sNg==u*Nj9k_GJ)+R~GSPBȒZ:(K]heL=vKPӢwq(NrG^ثϣ?#tC?.ͼ[ۅo؞y#%ǛjVyLSw%T*s92JTM%"YkQО.q)gCͲn8cgi6j1MѾ[{9h^vƘǚםidfi.^RHmg&rׇz:}݃}xT$ضk'5s-狶,\vpbPD،=Okf.c#cdz2FK5T!&)|ntD<+OŹU i-G[EE*FDfeaf2QƤM\UG_{ǹm%\yrGy:.\4wjPGUJޕUV7Do\7Vy_13w;[?c]H\$IJ,*L]3b%L{y.JRKG2sq,B6T}(#nW|km+q5] r㪍bJ@y{byz,b踊3ϻJ,'^xd،)JVw#.Vټc''ÝպWtbRؒJz۠8!o9IۄS95E9ؔ-e9JR{dmnｯ<[~n${~Њ$W?&ՐY_? #a.ߑv?oꋘ?&ơ|y^N4o=3t=~7!/M3>n8W홎2M`Qx+ z qy8%]7_~540ۦ彷]Wq CѡwkďyF5Dum_}~P(5.(X,K9vᯐ?leB9;Jhm#3{CxGE-S{;@Fz˙]=O'!ɿ]' r`:7'2bЖ>Iy,/eTy/V<.H?UYY{\^#ѣr9^7?xoRȆ7EoS_&??zϾM?(~Q-K&>"~aߨ t7Emsϛ+?;fCr)fY+>z$tIkjn_>vnrֳki-˹l= t;'EyC¥|/BLwBJdgjۛ$s S1|ɍV%JI6KvəhzIlBYɒ|0"Sy0F>eo5W)O+X˻u';v)2vVq۳kۮws?UʑBǴYO漪e2MIjPAک\b1)DDؚKm6ZWΨgȕ۶yjڳ 2ضN[C[|r@9Jfo<_eI7q.|cÊV߷:i.:$ȋ)1%%)ADZCEBxJ0MJۥy(bNsKM9k43IwNt.\%N簤I'.j|ƃ2$grBEٌ\}9:v*!n7M(ɽ]7c@XxƱԨ37īf62cTTfFK]9wntQHͮvٱI/f|j=7}\_V5U^+:uljSȃY(XI.ȱmo1甅jڎIZ2>#\*:gY|4k\8ZwSqtyA!+];бޞKծË¥e)#5ap.QK^8VdU{*ѽL\=qmjnB5>{ Ӟ`v±5 ^k&O~Oshɷ,;6nOW>u6{RqS`)S%jp\ipdEBLfTWy$GIYw~䲭J.1vSY5z.V>^+Ǎvc.I[R{QsNR3ӎfhd>y?UJ*}~[e\i5U^͛E]G_FS(Iɿ]i8:4zj~շsW,ˆsy:%O}iur]iF5~3M:Ӟ#N06)4ߧgdawIotiz:1r5YDZLHBSi;NQc44la=Y kQIT*ըl:tq2(է9VO4뒳܂~2rq'nrVZŦ[t7\oլfb/mlpc.I8콚q^1iE~䰳mi[dۧw֤ICfdFeCsg:i| 6擣׋* 96lust^{%99UNRvaMܽo ammi$em4D6DD\nA%$$#}۷/ݕr99JMն[oT޲E"KTaP+HGkŴj5TM5xƱOS-k`ۛkٝWz;{kS}F;~q|~^_|euwnE'pSupUP)V]vE+t =ZRaVdG6= *.ϼnj9:UɷbېmF_tޫgHjVS'śǕًdkkѻ_]Kv?nT>)^e=Ar1'3ԔILyD?:-^in):{7.؂\.:V }#뺾.3r̸*xbFM aȵz 6SQ:ײj[ 8nn iFMw rR"5M5I旘35f^j='j:nNW.ʭocZvZKV^ɚJ.cM1ZI7E'6rg탸5oZ=[m Z`\hbMUR١Ȗĉ):Jin!_7Dй+f̷eKҷvͨBPR(V`y6tw*MRΝcB.ڭTnc;P$8nFvm4(D(R#R-L -2:FP lxZKQc6I("Km%$E, 78uXIFA$RQI$JbInG]c[ֹ:ZM+n^')JmJMJRu{e)7jQDw~%yQl}BZujSSf۩QZ+Dzhd5o%BIc'GZ?}΍:>Ɵivז-%݌J5MqGWTVʦh݇ܟ~Օ_6 n'{3~mϬj'J11OȻn߃r Qr\3y٘+WӍ'WxEs^O3 o~[|7>]]H9݇ZomT@]?5B:Z߂'`V_+/MSKX߆ޠk3?o7y:4R/7þ] iG߬aBRU&?r&/} cQߥGj2?C5Yśe7hU=?+ x龳f-܈czW^7p%-(\D4h{UK&ӡn^m]Fݢ:`δvj俜F+) y[{{ 7 tu>gvrěOj'5 iRg[ͶFjGe n~qT$ci ۚ0oԹc*jL[sVWqj\ݻ&6"WoK:cnWmrv)o>66(F>=W^bf#c zzʞtپy%mՉPël e}J.\Zk4ttt>oEM=q)hJjI=ͥ(%]脼_88ф;͛gWG;Cw~˘$4=uWdĜTثNDkiQL9U*O"4XP`02,Ge-k5$h>ܼ]3vr6!9RQPIVSnM(ۓ{>;/Qͱv{3&-[rc)ܚI$n{Sv3[j00)-D3z}MRzVQпj,T[uVs0\}Sid;r(ݝJ>æʺL&c[jPK0~d(FKÝW\m]GTcF|Iׁ)I3~#oX%vҦEݑؼ5Żv2qAZTE^..M{ʐfȏ2##.R}*KʛZz^ӞN*lPťLf\G6[WVQquV]XAi)5J!,$iJ6o$tPZc;Kjx_n3`qIelV~vLy{fn匋Ѿn%;zV.n'-ұdd2߽1bZksPe3TI9)$ԩIN9Vơ\=2885N\ p)/a柛w9g_lױo8ݷ iixJV& ғRi{N^_oAŮE6Y7I$Nk$|Q)-*4Z)^¸%4Qm [I%.c-OV+C֧R#%ѨCe3i;w$G+_dy| Fzj$DI(=OA gj%v/]8qԯNIS*֩',Q%\44ZZ%D|Ǧʴ6&vֵI$%8(ԬƾS&#Z. }6z?b/|Jl{ץv&mpx4Z$”ڝ4-H%dGKfM:sKSRWeJAn]>s6应-W9'H]'uȫYvgK^\czp|My\鏩w/ËQ.)]\QiS`8uL뚛̸=J"ܻi\å'-)54Ue]:K\퓡vK xwBqrH\*֕TnzC.mT=t-H]SČ~Nu╏NÅ3f|͡G~B+Xm[Q7U{9"~jgK Zoʰ7"qJ,ekSeNGgϳ] ^.6:s}_,%eRg<5⿨z{ZPun#jRІ.6g T.!]xa c#jN$Zpl̋H WZu8WmMRýsĮ?Mco~sx TU҆Q :KDG4n42.<3/'^?6/ܠڒ^yrrÿr2\D}}B]^E~^T cɛ7϶Y[<֞[7d}2%QPqOLEQR\CIsj1?\}%tJ0e~ *sk"*)&ۓEi#{1J8Hrt|'ܝRr8)=ƔN'RVz:cf]F7bZyZUȘ4x8,#JG̒?.W9XnO]KO]%]ƻ O5Γ/3qÓj؍/r̺rƵ 5\&m6h.xoeX[=<3%< lZ"2h\Z[&jW3ejm?k&[]ųj+{N{66leu_+lj]q* 7g*knأYv= q ەdxЬZ|%GUrQ3jLŒqET]1% qkXYūYc[7Ś]QY\jko\</Lc7+'hMSUc6qXyؙ~6#ѯv.0$BQi5YyIhɍiy=KD!n3Vm[V%W-B%swa97ajۗ m+9~]fKq|Ddaˑ0A]_v޺mM5* F-BYHJ5}q>ʉ.6hyDmpD׬'-_v5;5[8K[viJ.3dR:oYHHh9I7:۽fi+wm^ [)odPѱ52CZUJicSw\&_s0uBȍh32džzQflcd^m|7GѹE!fO5]]H9݇ZomT@]?5B:Z߂'`V_+/MSKX߆ޠk3?o7y:4R/7þ] iG߬aBRU&?r&/} cQߥGj2?C5Yśe7hU=?+ x龳f-܈czW^7p%5|Y:SJE\U-(a_cƣUǽXXKiȞNlmۊڭڄR!**ܤMeȽ$|X5(Ź\rJ~ܮ]>'HB0cp XFr_c?f?7<ukSgov¥iG>>䙗i.+t+bOjIܶ . i^:nm}s}(3>NZ$2Qg([".>i.ƾ)B̋M8+"- >eE6DݥJnJˣt׻ 5.˅nJGwZD~!i۶a,Db3ZQ3O#KO5/֍ozuK'GbRi᝘NV_ҝcvם ZoX}F6z 7e5_e:ۓj=AB+iܔERadMBq*ԯ DwI/Gy*mĥiRKg6skY/#SN4e$-yXM YL?^ĸNNӪ{$r1JJRSLO]Aqm>V/s[~i/j+m>z}eI"Qvp]{ZԼ:{vPAG2=T͡@ڐ#u"E*>C;o$~C#_d/HBq^YRٽzIKbOm\~żjFFGdiQ(*/i*#.FF]©m=BmpQQQSP&Ҫ!T&^>:y)$ˑÐFčI Bӡ-t!bM WҦŶ'UZ=}zvn~oT/\ǒ'nr8 AJIӆz<^uߖ4eFC1i+v!3qNyߕni?4JZlmYFXFۼO0B\m[ tʄU3s"Sr(NJ;SKW72L4̏BVdf^Ҹj\]ȱ۪(ӷm?J-KEmWڽ^4<8qu%9pŹW~877ܾeVгS(յe^C]yX͹! םm4FGȋ\y'Z FX7e)|Gjt߹#gb\ŧq_([R8[qU$Z (ʻezV2V!iQ,i$JE˂٩ a(GK'O{vnBvryRd-RK4=qxZJMl_CuuIz @Rt㮽޳!|68\-l[џ84-2Pu" RJ_^OL>G1~XnBŬw6J0*Uvlږ1N G1q9IUm*'oWu][&UyYZbBZRZNfEJf"+2nF~Eû7n1xv.RUM$6 lAxSQJ&n5ܞwlEói"#>4׿Q.nEq7Oko[1wg8ZQwZYiqtm&~">Bo?w͡ni2峋NCEy Ҕ+%ZJ ʩq*fpˤl,~^Mχk1+:ݕ z&Y`KLӪУDr3[*Z :(SL&ݻ۬Vqsyԭs x|iI߽zZrg.:mp%6ԜvgmpIUt;QbS.Է) ǨKSV,*lڌ|5Jt3#NP.=+OZ~/G سIgbꥹJnl_DUM\iM!֔wVZuԺ,yV.Q>f v:݇WiaŸN5Ҕ[M7SsrvǣrMW= \8ZW-jsnڕ.ZnF2qt ً[ٻޘY۷Zm"Jxr&NAfA-݌to9s359݆mZ+N1-qS$D=17 x׵+%_ ve4ir6Z$FDڗnFtOr'7'{9C˨ꤡaYoace{Refnft RR"4%ʌm:Sj3)OdInTO>X'vxV#jܮw9Fog;5.~Y5\~18YQܹvj4+~t7S ﬕs %^۵ڴDZV69R^Y+rj$ԇoJKR5wB9C>Y:l+EǎS{ʲ{T6Wi* ^^9k/y/Cs\g*qڵgn4T8mERr|Ti+iPe;;.i\EBEJ 丬i9ɧM-ԼsGDrZ>r#R>~X9y4b棇9JwV۔%m(b[Tjvl}۩~nDԺ{Zo-YuK1vx.nWuO+jN [ٮ0%"΢CdTJK-RަH"$I(*ve &҉FzB,_Vpqp9m8werv')E;o&QE׵^d9˦j\_,ڵugZȻ̧8k+jK{wmr@3ӭ2 wFkzFVqs1؛.v'I%$[iT]D5Dl2 nk7qUxԫLS+sا3/ΖeZYK<["%-g/kRs:f3;*E ت wJ%)5&+&rw*霣i|sMҴ|;R+fm䡩.!**dӶ-6s6,]zAXMWjmnz%SJߴm2UXw7MQ%<!tKys#P,W>s;3IYwx<+i_\\\U6 u7P|xbn_k&ӓVOe䦒 VUr,-㘘"-LZeOSҠթrEvq8Kf%5%&K"#%vD/.ZYYŏ+p$nZkvއuW9㓱Z G wYIFyf)?ƎUm5ԉ/'k84{KO:rQI}XRuԪ|*lu)3qZ[mSm5R3".Xcَ5c®ࢫI*۳~wRϿQWޝ(EJrri&ۥ^ʶ齲Im|[yb;mnm֩uiܘq>E+Ikx߄3r33-5𹻖09ϖ9[Tz~mr5NsWl$oPusޛ^{Z;);sڹf\3oٹZmԉ/'k84{NO:rQIBø8Bݱ3n֤DiK4u& ofSȒܩx<˘|N0Fչ]qsp"}! QWw@t4ӭ+cO5%]'*{eM߲DRO1y*q8w++e!c߶ܪlZWّM欼 CQ̼빶lX{vib/V/ ai;x6~]+z]MWB>re-:lgk}պ!#9?%܋V-c[z!W?c7YNm/jRr[HOzԻefճ0q15Zp#rkQQ0tU-AmڵP/cȕ?0cZYj;:0ZM=D6g ?'UN+ձ[K ܖB2'xq9{|۫N0ku 7xaj;n\ 2[VznMlWiKbSk))f..)Km)&bGZ=>OR܍W:j'rM'wYz&/鶧{Sʵb"vջq[I-ՌZH._x*BagC'T(Q:$ͳQcMCKy?3g'ߝqnT);qs #ؤZ}OOI:cfnc8W~qy.;^pVl]Hԓ>^H^@7-AA܃nmL(uWܻS߿ Td95Bdh4t6*dDh!EhI[iŨ\L.&Nc ܮf^;$R)\rip9I|ٺ?#R.ZDZ;/]nݻqs\QE9M&Bd ]N mN*D>tgbK>+ˏ.!23]BȔR1ɝ^j'k2ƮqBQq[$di]icV/e`޵B.FIIJqbi>Ӥ|p; 6${)RU>_e}^dzdfzi %ekRVUS?6'hׂ)5.\+qUgzE2C˷ecŏ^֔ibk shesFWJ#~> Wk~ݨ}ڶ>ơǚ)׽ZƉo~B-ڼrvoE:Ʃ3ۣK7+Y`WirS):{>ڛ}:wԨ(J_";6R%[u&ƫdZ_\'np| RJwNeTW,=rrbnkڄ[M3ܴz)3- R.?:okۼ0TU'w{6&w7j1z3ON'fGoO?)S_bQ_¿R(^ԴԴG.EtMڇ&RUiW uQjU> Kiu1d<ѥIQ'RQ1:O/lŗᏩiʂv&Jc{D5 Tt)1.n[n۶X}RjqnOʽ(~[Ns{ސ⛌uO,kgo֢dRNQȄ .'6W!׌P朼tdZjFGE"]K@'i۪N;sI[{SOzk>`rRR+!σj8&TjlvA̷Q?HyjyLHNտJMjܶT۽lG?SnKN%<‘ nq[N0Sq[Ta(&t(|HGO~gvkݻTR4&Z$#ViOY1r$6YF?e4U/Mvxų:zbU^gQQ+NW_'4jfz^c'#`rvrڡ(IJ/J ݦ6 ]-CW |_{v*_q3^DZ}Ic6Uڌ8p7{crZq5ki`)mU6|-Z5^iEz3P=:Cu7DF'k%}<C-޹ֲ̱#\,(f88%X-N(ck0VLR~} G"-8ӏ/ϰKq?(#nrVTmZ;zióM4 m |UT'C^_1X.gXM{%ʤd 4\ovN":"y-,T)fLQgۢr=/CƹǨJVr[a+!rT|%Y\ٱzsS>jͱ.oOc6f$q% ǒGo;n[];ߎjrk{~\VۓNIGn:iqxo |~t5)Rxעri{Vi&NUOl_ѮMfsޕkЄay.0P{7N((BaIP$ K"U6Gl ݙqJRu+qN$ m#*p<|{:>-Ev=86N*MM긭U*uѾ?/^o7;'u,h4݌xښRM:5.(/ \իU.{F^rmF-Jɷ.>Q"[4xT^OZ~mK}T0ݛ^SAo9u?lX(' qj%=X}"^e4wˠ|rܫ 6I\Ķ;Ӻw!'ڍWg{ i U_9Avhۣƾ+:vs/MK[ɭīe{`Zgb}r[i'GE2J7Nez579wRq+Un ]J.cJ4M:h箽Wxxm^ pc\wcN%'My $$| :$Fqɏ¾^қP9J6Wxvu}ݵP>Z'FFdg"-; [¢cmWkÎT8nG%ݣ7*\խCLRYZͤiD&J#'ehbSyXK|y*ӞpS̍R`[pTr/Eg)K+92{_ n3zwz'oŸۤ+sOj J:`T>Cf*lwd\fYOP"R E֢̔L4ɥ :;.b(B02rJ蠟9>V'9M%)IqnhP<%,r'P/vNSwr#w"ݨaqc(|{kd=^0jTMR2ULNz|.<|^PfY22##!,K~E BEJۜ&jRNsHަޛg\r,v؜.jK3)[EJ2ii{KEiHP^&]Gn8x=K}Wx/KI9-ϵwQ%spܾ[^R}S3$qvq8M[ ozKxcqmJ/ӿ{_}7&ݨ\f6ZSyQz& 7ۉ[8~UNn|nkiTB+4RI8'Nc%tn{!]Ȋo.nEmʱn𵵥J A+wy#+ikǒڂ;՛s85'KmE:Ђu""Iģ5p=БbTY-ͽڔ詻ngL2Q}$de# fs^o{DUUsfwӶ;s1T,ǤtޒQ\෼J=.tKU,7čJ5 N$y3kdSMQU~mO[03 $zAڟsF5^뜞"Կ QHmrR"ӳηer+ҔZ]hE-6Jmt'ޒ=O[sQj)6K}?e4v_KfZheޓ=BV[bY}lݒTTЬ{ȫvO_qpRApVŗ 6ju=*BR)g "O1yhb=tqJ gtm\b3RY+JQ^Ō֍\յ\>+uSi{=x ^w;uӘ#ĸzLn*$anok߷CBӷ}5Yqvdž<( "_OWit5:EZj2 B ρ1̊fi[n!HQF82q1牙nqnEpT(2RMoM4ϳOu ':֧_Xjsg jP^(ڙ{2%E͖j^}ZU[Q$'U) <܂%!s"m R'G5M0<+zM6qYm$ڕ$3ǧH]?o2N<8F1̻r_my[Rf59NjpzBnl7*{.QP 3N&^BLJPjAHCK2Q}$#~YMq8 k(MFMU)8MEqTy+Tʞ-ar5yܕOXw!e;q-Jqܶ䓊Y:LC UE{/t>r"lI9)3KJjϤA 6SEE$d߇3KG*En|P\ԭTn6I-ƍKTj<1H_zwGr19wF N8ݝ+a9ɫM6mhePi%mmD! """"""*1bRKrD"vnrM۫mmĽm]ӡiG~e"˩ lhRTMk^MX["Jݱk7_ޕ*DqĒ&flՒ}`W}~SմZ{ĕ~wm*/{{ѹ_-0ط#P]xlڱ~Tn5wi*lڪ (JxioϏbqKYR|!|KN53 OS222$jzww%i}>N)E+rۥ7c$Ofl/LNث\6H9: FY󡈾I)fB֔JI_ ֣^: 9mY{66㒢7Uj]:.-os[R&gMF3˸#໹kmjq^8W"PΦURjʄWa˧T!͋ lW48JB2ko+ /Nw QwQzQ ے%$ޓ7^YL|r7!v%Trܥ &|M8~ybrn[RV gSn{{*#2#ԽᢏӴHak" ӌcwҜw&RJ07ױ>Ļ =^ BɆ)v32.M1=#6%̠tҤnzqMwԣ~s*%-j|_m*.Yx9Sz=)qE4 3pk+,`=kNRڥ=B=nŔNAx)Q$ԩȧ4z3t#Z2lҮYn$S%y- JzGpu|LBV7ZW#;Wwipܷ%(6jFG5#{$D"uۭ~]֫SrD܃fҎӾ+Tu>-ZTQ& N|$沸ii>eRWݳu'[O̻j8JۻEѩ[]vni= ڒ,[_%kC7I3Nv$4ɎЈeٸoUu:[}Do5|zNq=Tre%ɧ6&~DȍF]ƞG5q m]/w/ \ʲr8=oʔe9U(W"|S]uZd#?Se[W"ֿh][-7Nu:T=)R}.;ml*5Dlf $fF(̏T hiIUU4Szɕ t(%_|2 ~6eM;TƗK[f&]LK^CE2[ȏBOd;Mi|cx,^6;sیGpQ\NuJIFTJ~đArh* B"$H쉩eXPRj?sl"ԥ)su]xpԴY%VESH"ЋJǰ K&5^Ukzׄ8kEgS2h&Se\ Yl]WҶp-ZUvi7QS:4byqOo+[̺腋[6-_Fo.6[7$p&^ _GZԸߍkc.qqoI[9m߸YxOZЦ1uoiSH)P9Uʄjcq= S>֙NeR><;+ڌk%_qT].srNO?s[=vH[]RZHRMtᩗVؾ:/~u)ԍdg%=edVrISb{6vSu=(ܥ)mTv/J}̇8 S3ad:^hBSf؉OɔLhI_1d8,L><_A0y3rXq"'(۱;mFNII.v5_(^q~X>y{3צ I*Vܛv/jW' T'NR'j%ꔩ:mJ3SB}΋!-H-RJBТQoedi9tjENenPpke.%4]#{:>mkEɱdYWl\\\'nRM4&U>?Ќˉk÷!𴪛]]5}UqG~ݏI"O~s6(Ļ)qO~h}uԕd}Q~G,oE!&G&/]_H-O=o{k\̭bkv.Ô܈+;arZx)m?M\3lU$mk-CFXjTv6u' g:Vn_*qk:VC A%'4JV%EY)#BғO4<e׿jQQ]yUr4=wm[K1r׵%Iũ-O}|kC;/VcݩWZ)EHdžTru]8hgĵ-;=>U_ InvTm_jBM+QiF"9*{DI/iuo(=TzϖmPQl_v4z>T*ȴ>YF;ε\t]EH4ꌇ[VrLzef 2T^V>g2~kg5~Nק;{~Z~W}&ŒBӿS2$J?~(Yœ"˲ߩ\O]: J׉ښT{mmIѩn3˧)4LdFZ/zUG>U> n 5& ϴ-KJi2o]uKljvK3$bԔҚV旧iY5.ίfi96v7!v))FJM4{jG~Jt/lUE%pTAFe4qQk\ve۽/u/Im+W')v{\-E|Pms7߮DZRr۞/mu*1ՙaB܆ -xg3#6ۥtRogʌU)׎]ZҞNnŞr}F1Nnޞ;cZ{N}ۿMiuxʉ*3qi'9KHQ$WJxXyرŔe~[v5~/jN9Q4o6rJv FrdxM*iRjMzUinHdн7ᾞS=S'7 } ̽zt7K|_g J=Lq+/Bw_\ۧx\HJUPzQ<hqF[V0x==CsU7q|^ {)Iq38$_A(VgcKu06Ƅ"%i~_ˉk QCܣB8Ku/񋇵u([w}$F|8TՠI.E !;RJ^}MɒD_q2];Ɖ{5}*n7nEInO{Mwv}&q+v [V}Ĝ@%>#dXQ$f;iep.GquixVt x6bj͵mlKقQ[T]zs/&yەnM'W}!Fp_d^Tu N{ɻ'l{խ2.sTu{W^H&;1s)Pӛ6>$mě;Łnj= fLT)>׸+qReɴ[UR\L*P/!$Ӊ3Q 'K=m~6XqW3^W+ųO_[F$rR*u"T%@O +%# ]˽!aܽz{ͷvQh쩎]hGތ5ɇ*DzJDRNLi 4:{~2FmXY-zzĽ^f=]uū{/+&c:Ma{ĝDp2m܍kHș/(--m_vݮK(V{R}.k&yƴ7i^4@3f sK3^Ř˸B=]?gt5KbZB<e;kQLpxuWC}n 5ҴepB##~q= `x]KWF {GfŲ}?G.I9pjWkU]>={7q{kO/^I3==f1ɏ%nnʫ/Zu_yXN<57ۍ'vy/"8넭M2eԷ&Y,в33%IkjMr7xf nmQkX4踼>a-GcIeތw&U=-:qnW)z¥j :WqSZvԒ#j"KrIU)%qrmRoDGQ~SYRsu*V)  ,/x)MFD6O#]z 96[Ui(JRfw'y$GeUީkdMF-ݻ98F2d[o{Rn0n-xsV6Dh|Eb2E:KCOӪv4SJCr"J!!m,hRLD| ZYFm/X~ΧfrN&4Ƒ=Z9Mh.Mܵw/BdrܥniŪ8ɧ|y%œ[M=_tj?F!z5\evM:\ ~F-sg钬OWq“iiȍ<Gi%%n2rqͻllƑ)okw7}\Uk-:&fj솘XerV9yZuʼşdFC=rmo%~ZN78X(N)_7.Εn1MpJ}62jjJdI";R5&iLԸc:jmqiQj$ujp\{;v5B񥍪Xn Ą4qOERjzN(Ga٠䌡)p*v(J7#ZۻZ8O W uONb+^Qipv9GvֽƼϯrYƖKGJQDNPhRJjᡧC"21"9ѓS1;R_O7/WGz)8fE%F2ukmvSov/iZ&/]~KmI[:^~ͤ\kMi稜\ywJt3W7 8Ʒ~ݥeFgѼw"8VVSج\뻆}ݭ/J6Q)d|)zU3>k\L=;ow֯gN3pKѫ|wmkZ$z^2R:E)f>ς нd|#׆?\ǔpV{;\$ƵE%-ͪm0S6[n< kE[}mvE4DDZ^$OZ0*$~XUv҅B@^?]so#%ojw;Y#SxxueBگy v^i-)s)zV jC{7Gt.w3v,ygg8s]aE_,*E tY5k٨h=o"m泏:\6w噓aiL׎n^c\75AGkЯ0Lf46َ`egZ˓p/k;̛]kq!ݸzpԭG"}R9Ve>ˏHUjJ-&7nrnwG*Xv\˱/vN}O)ʼn&CV͍f̵]r\PMB-6Du-#RͰtRN^)mT _}nSȕC*_xBuTkJW[`ɩ`ejvsngP ڻ.-WUtܑqԹQj)t;vN&RNũT+8%IXӃ5fK՛-d9 ]CƑm|nZ-6=Hz,*aEm W3VzRšdY~Xf׀Xx"]s;)5u*ُHB BRGS6bݶؿ 9j[1*jױga7oX CUI%0v#~\-O-Ꙛuɷ쏪&5mY٦M`LJ2qK~HZbr =N'YobI. (^ ׾{_ ?OJ`S`3BN[}5w6:ǵ/iSlt=4F*d&T4y/#. ɵim5Uֲf 眕6Y7 fơ=3dϕq뚩$qTM-%r!$@A? ޾V0c~{[{;򥧅a~ڵ»&ڄv1ek=wb MLkNAԬw-x>~/r=e73VeVN)K%Sښe"+3uXuچrn ֺVzscJ峻m}vb㶓n\YbIUBT%*,0nov=;z꣓S/nSXSpl##k9mXGrZv^Gde!ŷRԠzQyjC]`gToPov{j~KRBMY}i[߶9KL2ԉO0K#m>wB[ٍ+n[[b٦DX ݲpo] [\m5qdT()mo4Oy9Ie b][wղmM~vmi۱~t \}$яimRk(L c Cvk7r9_r1 ;zv|F@KyZ[&jEji/"6$69ml#e]9s\{ScL}Ȣؿ0q/nZ*t,CLoD߉Njǚy=Pgmu6^]l-["çUʖMlʍp-"qmU>۷uFOJ%Ǔkx 'g=睋k[3u,{³WɘݪF]ՍeFX"Oy\,cچ=w/gn Ļ]#2? vqy-gXnR.^}ݺFs{ŝG]}e|#0mjx"ƬWكm?rgU^xVB":Dt>@LRbun~ݭ,w+v⪕;\U(RYa61>#Jm˞Μ9g9XKaG='u8gf}'qy#ɉw J]We.ʲ-<+&q%s?2dњztҼn`cΤmmqMdz O[-ߩӲ&;[tmܝVnr">{x<8U+p:Ig]zjGkt,uzf}dؠoJaکqEq -(:d<պ=eKy[˗^%ZXkX[C2߱\ITTLGzANM￵i]K>UsOGDDD.ZF6* ҃V Zhz{'xp^`wo8r0h ZmJ5"jb[l=yUu7-;7IT%:jFjߖm0tzU'K)څNۧYJ)4IQ}^KWm7kSP>q;ނ#)'n7&׊r?óM{IwR\j2Qn[v pe#/tAF\ϵ225q֒om6z})6҅*oqDsMf CNIN=T S2t,_ѧ}kveMF0J\Rnnݙܹy[rUc-j{yGtkQ%s]5qB.Nw.JN1LvR Ui5J ZESQԙr):MJ+g}χ!2;q([jAud][ljVK3$ײSJI=/|&tl'*n۽f.frܥ jQO8>&Z];.|7T/C}$ڋUmP2Reҭ8hFF\L 3~e v\۫]ݝNmrnB%*]Z«hKc=BTLG :V74$=Ǘy+EX'4tn(I:Ѝ;Df8c,k1%dJ6.j6ź{N~l6&*fœI7 WAlGOu-ҢH,,(ǔe뿋쩨kM܍ZſgRvQ' 9)?n|er˭|I|-fGK.rΛp8XV1%K6mvG+tc+qE&ǸC_Nm:l=_/m5^[dߌڇ.c<%:)tQ$Ow~-aY;UJ>=F)2[nk؆?훐M=l6[4(O.]2#-H^n#->&mp5~Fӛ+|| S,xag%qkEUzUgæBhߕP(7]kFnq?֖CpruZ6*rEڊtS|*tI*E}7R<,nUU֫^I7Q*mSly%rdȓd8hE<9oHhMfNSRj[i7D[Rj݊+kდq{"$$H?p\̅S?㭻;t~R߁)^/>Qj`yt[w ԛ;²~+ߔ_ YW~|o]?x^ᯛ `ʼn;g)T@vWn]>&4lp+$D̢1l|ȨF%-}.9[}w~ ԠLM9hСablfe&QoW!s?wjLK?s7yO>(=C~_nyǜu?v3vyo oI@qV-jeES^[9WoSܝh"l2C1a͔CiJ@3:Pճw=/7ovuk+\V;lDgն<[A+rX~d;m!_s8ݖ׷;;.0llUC+?i#_crʙ1~C.\–q ul8Hܶ2m`ܻM3Tov|Bs rɵ"oLS- DКw=Tv@f'6|YlD͓Y%׵-#Ѯo%:&!3o%\J<02;K87>^vgƓ# ;ݝmz^Y6=PS39U%~ &f# }o!muH;ʲŇ˷yvP+&.7e[3'vR4Yj̗IZ`e˽3o[WU{ m[sUbۋZǾۆl6~9'V*.\S2<Sd*zY[aŶ`]C$n.v^Ʌ dng>ەZ,Mmϑ :n6nϦezWqUJ4! ۇ4R! =>>Fn|Q[{pRO17ƕ~._I''00k=b՛o}Osðc2'o\3}ݭQ^2 . R1yKȣtAݿ-uܾw!`?1Whn|gzUo[ECWwjUIן)^h#1ɭ!/Z np;o;ΗŻkXs."6E`Z1 עӐ9Kl8qd q} 2Stt;#j>;խabONŗ=fwP1j)l6J̶|gV2`y/0E˛6+ԫ1? 6}KW c\KoKͨ2ۅFw–s*TԞLיuDx .kCzWXhy۶gLu|%TnupǺl-S* PRaLnT+c+*xl.v!.U=|; !_L̎뱚U=4hm:ٯ"y)$:>%(n}X'p[ȴ ^˒4kƓmzDx \ 'NqamP7nyN݅=j7%McSڵj%STy qXymvCg{w/w=wSW5r̹u erծˊsOm=DhEҚRb#n)QOxtվQwe]I}wCa'"[ۂ-z}2UuKP$㜉ԧ:mc<Ý>RoL?wu|%ҷ&K y_!y9 ??:tq3(UU-lkS'ɸ@jdzQˬR] EVPW1DJq2n:,c|ǻ̑;y{X,ۂ.u.b˕u.tKBjQ"[S園S`ٮdNبeJ&9Ơ ~0a(Vm٘L+Jr*vڑE( x0+tp˕ n';wm-ޜMOxX>{#2%jgb2M[`K*\5@8l'e=0u+w ֘鳾{y܀:R*Ya]"Ӧ%ktynlۣ65,3gU}{GYrb;ge'TKwǘ.,rpܚV]Tr,!dp /ԺU,xՉ>s׽~W5oTh yx?xrrx?)?ilbT׬,z$Ԏ.UH٠\U1pU:]JwSrGZq8àd驐,N67QYBӢD㏙W!Q25ϸo9ms-7-%3CihO.J鯽-;MZM8ku-7k9S$8]q2E(}bۏI[DKOK}3KUB^u %Y,u.-&f#]'܆o$x`Yu,dzwM;#oKxn;\[d7}Rb+*Y䛂ZuBӱl{j0O̓}LhK;[aֶaGL{Cb#S.T[>߃F]NK"u^LUʐ_ykW?!GRj29͖qa'0[npcDvV)qz9R)PۨM^aJx W] r>];eN3vxdmĘ(5W2K1䪖weF{mE/QP6\u54x5[hۮ-Nk”i[lUgL]J}5 S:EhiUrgHl!ŒJ$pe=q^b͵Q' ?6|R\,JA ڵ"TDꈭ:ymg`B5t%M] <N_zv2_Ortٵ/i/ReӮ*7[qүqEG* m"[I:6e^p"I$jԴęh!m)]GZkcjS!{e^z}+Cѥ9;R|/ֱeiUԏCNu2Zhcٗg$ݭwvr P8*7/Lk~I'Km1+MW%Bk|oOm>-#qj*|Dbѱkn|n{v#jĮqNpMIUm(7Liz;{ҜݞڝVƚVϬ+sO!OstGvxӉ']uӎ4g_ 1^-8ۦ k!)Ύ5O;YSB#2Zzχ;<.ֵOtge~.(RC#wFZeGZٸ6FFJ4e2ˇpJT$[wgV)q6muDGJ56q\I!̗ y/I~RtJ9kJ]Iy*'FN0s.[l!fw'y(7$œ WƫgyΙdMEU JQJv̋vmrۖ.jWR_M֨djYgSj0^\y'EoECjm$ IƩK>Z28J2TiJ2N#}.s cArl嫶nB.FIJ.)۔\ZiM>/hLĸ=C1s[?YMqp|94- 鮝𦔽/k^#NT(Y LS$6˩}{;5 )B۷W$qpN)qqoot}ZDVә;7TiK|6f3h$dԄ}fqݡ>Nb򗉉+ͶO]>ߡ_VtYf79ڰիF sq~prս|QM)g%l0ocJȨHz V;Bb/kLAcfPJ,ԭ{ƍgpjNR6VSI*$!yV足jᇑ.](EܣqM\qJ2eZT).<9UB/(B0j)mtKEj#׿fDI-=rZړj|'Nڤ]k*i$5qt"ݙPM6E4ke^Z8ۏhz$Q(R Ay2zfRñnpnkbkI:=j &ΝșW?׵d{+ύM'??XqeeĽ.[o=UxFS=ӷdZwenՄ]_X=ĭVa* pKs0ބۍfJ3 gz̚i|wnxtjc¼5${(1fXQ65ȼb̶Zkn>%FQMJXӡ{TZEVNᖣimT/37cNJUPnP҂ZOE~"-Rc4^b- FEͧtf5[)S!OZIښݲ͑;tvܡ+N)AR=hCNn;wL16-:特7M$=Tҕ-.R[HٷnXk sn[ҞD-0WS9p9:-Ϸ-jѬNu{ҹfv)[Ľvwfg(ٷfe+0mYj8Q1\ݧg]Eǎvڿc!4#j5̋C2"}BRriFp7=ô\TZ:\BLfj#I22װ<;صZl j 6:l"6]۸ K'6RTѯ^ئOԓV\?$x7s#r:Oh{ց=MmuHԷd{pN /܅:UE#Yy+(SgQ(Щ)RHzw>^Ѿݻ>mK&^ '$Jۻ&w%F|xfz%˳ L~3N?Cy9 v w/{ƿ kz3x> sXv}vP"@WyC z`'톽Dw%-tt yVY\wmuPYQA0iG-2JP,6/gˢ]u.-n!Zw.N7Q]Df}Q0({a\@=i_X7gFǘ8^⻲}G MZ1)WEfO12G+=-B@z\`||w6ċj߬m}UwRox֢I &c~XGP6Qndpvܻul'V7^FJt^{b^B(L~sѣ6@߿^xqU!ڙ5|Vpvef-uӥ^3  FSDɯKD%0r}FF穛r7 +o"V8tv̖NQU!5uFd"bCr^bJ=֤fM#ʳԷP0O-9xRBm\=`r-:;~3Tl(nXtXi%2Vٛ#vwqƴ`L@"H‹qW.j,JM5B[)WܺUeZFqc'V˷1W7V̾-MHФwn8N;HPSdݷC7&2j.W\τGŎ'Vb]c.x+Rx1%C2T{myg[qU|+m:M:շ8҉yWd)ՋWS%%:iqlʹmGwݹ WnNŤѩ5(9hTٵDdGUi-)vSs2 2{OnT$Xck n:¶(lASLeȔBjμPpTb2~N2~%^k[ܗ[Jzs0ӓHBKq[}JَA-$dFQgjxxFv4r/x*Rm% `4J(&iv7SkԲmSH1YWmx 8n.k']:Z˭_W >ڃXЩ. jTq%Aā[E}amc]D:rmHRiu:uӚӢ\p(5-q%e)(۬ҖȽIf<߽pr&ݫVfY91q2ĭEQgYbTGQ&,yL+N$[q*RVۉQ=FuTܻ>f>f㋳8N6$܌n)9&»iˤsX,݅܍ȩv+sRTpO}d?Wn/Inpȸ%O]StQO|v5\}7Zwb.AIVK^:wb{[uݯcytO߶S<{8KSRׁH̏N7ۚ[xkwYy_'ZӵF+>쌛ZUĦreE9F[24De{}@:ExWs-\ǻ7K-\JNvEk%:s˙#κ].oͳ;լ7wB6nwu:$L; DkI#Wz.:Xp(˅v$Sq,wn\qIN-e<5Oe+vuYTpcojUI_ާP8 O 7&VL8z$_B-H-[uh]T{|8=qVRN-:Ij:7PUtXϷmy鉿:RIM~33ӸS2#׳GdŲ5+/Bx{(WzȨ5Y㞎#|˖+ ط.|e<o/rߔX>7s}VE.OVti׽ .5nNJO"95{#q}Ay9do]R"M6z\tnNS-D!@3N_jicWsy*5uٮRcWv/.,j}=S)j5C^> Ie =gu9ӛqjtz]۪TMoߧI!Ǧ¶m:,"[L!{qAv-o 3{"KʼnrIkfٶj2ƙ؄S`7` k6jzޞ?e5G&6uʷ2%ԒRKE*G\Npom F/V |C0.q_eenƣ<5Oh'67ɪn[SĽ{ڔjǘzs;~׌(ۂ`ܢ1ƣ` _l9Va6%UQWh~P~\F^ZHR@:ۧCJ{ôGeBh;~ۧnU J\O+n2 RҠ)ng}Kh{5+S×ܛ.1ZjG)iRȤIN 4%{oΜ/eO[Nffd ĹK?nnԼMqX'܌nZvq<ķbFnͪaQ`5 s,M_լ?-@_{w{ӺձJ}GF[%v\5[ŒGkOw/ΜM9rjË%2+rd~+󲕛C9U۳r[aJǭm|˒LAʨSCq[XMۺoubfp:t+ΤĻo ][ zt-*67kvS7D·MMCQXm;)܎n_h%]4ܙnRk!]ڵsDUF"`R, &#R_*[z*ZqFXɻ]7|۵w+'pFDەs=r./ᐚm3Hשy yD"jHCr':sA65نѮ^o1V/ f;nFr3VM)e*- s D'H݅fӧ\*޷[k<7u<-]֍Q8R h|p=WlW3s%Q %3l}@U-K6f-NϿu|ڴmWN׮[׸F*mW\%r! C78:޳vBG7ŵ.JթԚ2x)ST!řn~9 W:Wpܢ件{xf8ٳwKE ҰWxVB\qBZ 2wMb[lGSnyԚ~z9ZmያvoN2Afnݽjf>)j3 !;gOYʹK" Wftڎ+׭b*2ϻK>ۢӱeyԪXISUm[z+ugX%0lϏnvg!;t{BqPj>PyvR7Cj]O%+ݲ :qiMj6W}3vC/R=4Som]ŗ=ю, TF6U_-\6MyskwMr&Q\wjKܩyMϣUj0*}RZܷSdY3>Zjqj6TgzpA/M`/Cmл,޻feE[/+uk^Vs1W$G(JsW2ٰu*߻q*Y޵.Wi:ur5T),=0uRmho.twܖiYwrWHntvEj8qhf`Ͻpf(R&>Ki%I7$QӖm-2 ~yߗQ-앑/ x[k8nw.c㩵k}]FkbJl:{.(˩n0Hqvαp7 귎.Gupx[N`Yq'+ruU7[ү+>!xrȫoSo]OC# d^Q]\>!ƛGw^Mx"-+%vdX-:M2UR%d>%l ioSu6lsj7D P>XxHz Ukà(n^Q V>5cVtWj SEiJdznyej[lE' 3kuٌNn4JW)gB {4 j6&]' m-(ZMEz8cz>WZ6#7+[,MR-Z!4ܓtCyE|umj1ƽvƷV\;%>Q :#Le(iVz5 4ũۤUWxX ^(ҔsլB2w-V ^R+; ˂M\z+Uwr+RWY⺧~ Q*JcYSNSλUd8in=v K낫k\IRרSUaCFmϿ5̗P|u ZTԕ}>oYѲ1sfP+sQkX8Gb~6r,s>^\,mGL+7[n-E\.Fqḕcl*Jmjb5 ,m]c}NXfeVlǸJ5eˡ$4%g~N p4Y*WwW٧<8v#;qԩTut,m"#Y D\5V`\\Lȋ];LȇiS6ϝZ l>LruR\v=ǘϔDg=ԈdFZ+M{=|,[;0>RiSi4,S5}yxw&(E7&fݙ4UՕ! ~'Id)]ǽu2K-fޭ \08Vڅ쓬=Vy^^ IhyKR-B#Ըr=]mܻӾ'*Umkoy rTqT_i,/8Q^<ݤ|4ԻO(܄"'5N~#m.(Ҿ2i6Uev&I*<}҄$eNtÛzyWJubW^iBW.܅Wڮg]irO6Ve90sgv.+sV޿aޔ[p?3q*FutUo*eL\KM'EG*ZcAFfG5J 5jj=MJ3OK:k˝'NMB7m3uFҕ\-Ywg%PRqMIyZGY9|μvn߻5cWݷa^+X֥vnݘ\v7m>Fgzv"-;Ew֝}1|RjN𿊀7g#֟*GQQ|#/bo]p$>_Un9гUbn9׃ErQBU-^vDmVh'<R[fdHT]*~}3j;nvjc7s-rӳ Y8[n[1pJx kX[Jk9Mn!_Nю6x:iZ˦U |߉^Ԛ݃hYxk &U^bwKk.[jE+P(˞=9j@snCv7%c_7=xǁ<l {t'酚+1F‹l׭:ݻILruǶkL-L(K0L1&>wXB(pm;1fpnlp֓%Skidkt(U +xulo'/ڕeN r=^pZZ:Pnj8Hf"48ijY[ N[yZٻ+=  ø:3 ?^ܷ^Sr#YK[UF?CuhC b]GM')mڏsNrܗI]ljq6VB. W,UK"YX5{c >Iqā> T:n!,5l2VzCl|+I[*SrjnS6٨y+x,@>П.g+!rn9>N|W>OZT_ut Y""v7|sfި;Pclm EùN,{'fNT%U&LfH8~1v>Il}统u6P˗c(WV~H^bMU.o*oOF0N:_:6Smr_.b+|ݶYY غF,mwjv>f*>QM뭱Sd:`N{l/⎱;n-z~"Gze퇎J5S KG9!Gn;N1 ݎ h6m|S?ɂ5'WOÞ 7|7^ao @mxGmi^jϽ>01Mf0լD3-2T. VXR"ɥV Kl J O7|u?bvа;6.eߓ|[1bmRr,eRz`z 6܎-ͨku͹Fː dPhYgZUj}nvX;z=gVեTv_J }\1n7w2J?ޘγc\E 1Aޑzq;\r]]\Y&[nsNei\uURje*Qk2CSl*xJz-xٶlm+|UjUؓ`Ladqiĩ!Gd\W~fz;Tn*PdRM&T4`չSWq5k훶(N"Ӎ% V]֦wb.nUO!u*J&Oӕ2e|Z=eV쫚΅g#+/RW:طnbi*Wyo)p{:ETKؚR(RY+r웓r(IF) VmȵNB:h Q1ғ|u8E]{,'$-TR[j49l*3"I鯴zhd>Q+\BkNF=.$ZR4Nwհ(IpNi.(Gi33#33e$FXK*NdWrud[r{xnk$v2ıh+J1TQ[#JQl[tRO]LHKٮ NӍnF񨔤֞Em'MILB"ԋ%dBŋ+p̿_17jzT~4pc Vo\ƹb9Rq-'1j;8ܗ)hE%DZKS<璸Bu*%*Yw5ڻ9ۣ^z4U; Ñk\U(o~G?VUĎ:?P?_F_Kߤ~ᓾI |pr.Ok\SklRhҪz{­P .}SktZ7UQ4ڌIM8̈eaӊJZ%FFZu,KZvln廐SNFIVtuNi?CM5]+Ph,{jN JSR$IS^tSUVrORYu.9WyP6 [Kiu m!X|]Y79ӄ)\ģ)pbڳr%*&ꑶ_-H*dzk)1 V3')UAϹٶWRxe'պn۫h7AR9 EAJeGLms!%D| A 5]/Q3eb̄vnVn%za\m kZnv([emqrIҕij|""><hjJשvvǕ|Pޟs}V~2&Z?+2N&Z4w@)4iSڪ_>/JN9Hiۏuf8'It[ȲR.hZ$ȋ_Y ~U<UUO*6b)Ovzڜj\R̋.$FsQuҊj^נ䈈y<zZIuP[}Qm=C?zN(Exqu/kn S-FzKZzOסӽjJ\)F3b!r5ٝ|;6 o=-3*λ]αb\abqRi-w޵⦪~b8Kpo)Z=>)ғ"5/GTZLE-輵f7ݘ۹~+&+w/7GFI:l33fg.N~۲\2|*cnermnnM+Fq"ѪIz%j =YW8@~gc/~?N'?)«qȸs➟n=k" X“m֮VreMh2[uݖ] *FܖN)MȐ`f0 g,C9̑o;ddudJ=In13:ݒvvdMUEJLp^,6t-@͐9'{7m{-3,>hnF;ѰM)->>+Ěz!R* :`e--m7nB\u{b U>[8֪]6^ߤLʦ\DFNo$$dͶlgno8OrsQ\l̯hRo8tuNo+ CTxu!2[>ctFpeޓƻֶR"3QrQuOѳgwQr;S~)6HhZw/GgVTmUf_yt7%$];zLWF̰xy2Ʉu!MCmš_0[W6jf#a-KLi+3Q7c^qg%s<1aYIQeZf+}>;S6L0]Yu_h9߻<ƅpmiM$AVvŚ,*#t2.8Y)-Zhshü97/#Oro"u^/uFgWɺ,p:6a,^x%$Yve^3PƗMnTP&yS}OJ '덫MH^:rXԴJۋ/rI;S*,+yz1hv)Qw^ڍJ2oL׊q(\fDj:^T%vOadɂnS}ZO)N*λdaȜkG_PIEO}нa(^iQX᯦-7^)%g'SJx(.S9zVɴZ{E ))ۅi/s7 VIV-|sj0*UBTHIqRf>FP$KqN0 R̻8j\GcC}IUz\i 6F)Q{Gҧ3qSzKj-Az VЛS-zy:8*mNk|D鿓ND2u+0Yŝ7kqm·?8Ib]u>˗^_>(]vӋzv+ݩ){vZrJ2RQ몋C$z [,pp,8mڊbR]Il .f~d/ݓs㓓mͶ{mgjQwn=Oic9ܚm4Q/6ݨ[TƧ?nԶoytf{@AzT{e{[O'ZRZt~AGD?s3􌿂ՉIw'|~U\ w~di:Kޱ)U/sU%njѩ&GSP^ǝd)..!^U` 1wX[aԇSxoFV6_扐)T 2Mfd=ۖͭiZ7KK Bi9%7@<3<ճԻU,},a}FRqɛr i@ONJvK KLN M, ʖv0n-]DwlI-X6ܶ$Jʴh5O+mOI+Ra瞠\ MG7BفjYo1#͖0V`Ѱ2M?c8>-Crt*JkIGS:e#hPKx[鱼>{5m;wcն&>j-M֥^َ) 6yȜl_w{-ō̱r> U=]iw3)r*]:K]6BdCTZ|>gf}LW}[$'Y5 &c -j.z6R 67MԷFMnÌwI7w5E}o޽+K ֵy4܌ȥW"COyR[q5Ӱ͙f[v"_#q{MV6܍3"u9BK(41ӯqˇc${ߝCi6I(OmθzҜ5k^:>Jzw.>qV8{vU[ڶEm|DžBz].KHjI]x;Mɗ{m,qZXr忇2u^RO2Z}ZێS[2Jen!*NDcrBUً4<ǼMҲs1Zw57c3&ĖڻzmP*FuJG1-dN:|OU}ҵgi2t~F^^Z.VxjvŧnNNh<:]^~NN+ge^g.SԔGFe߯'[vn'(ScJ]kܗ7eJOlRrfziݮq̋S"\*U<*W]k$FջV}? 7g#֟*GQQ|#/bo]p$>_Un9;l S VvQU%OLU{οmU6bZ1MTx%!֙Q7, J=!3 ;Q,ڌ;6ͱ݅q^&ߔ·n #WbwӖX.HtG)N&d̵zpI,n cu ޖUj+VXUp[w]N o.J6Z8Ts&utxln;~HPHS/xw`G\ʡ¿rj Z^vt"[L:SD\h0sUwR,}[x^X,R2Vn< ]2YDr[SRKs8tXb̷G?Ps Tv 3be,zVz D[/I.KOEQrm'$7|[J>r S`5յwT#\w1FTz\Ԛ &"ׅhSHrD\'r]~/>p;:Piuu:"9ő=tTaS7V2rӷk7mb[^WmPp*[y.Þ6f]cizJCgRR@UVl큝.WJP1N{/\whZ ػϧӱE7|E֫Sί.x-Y&pi%v''-x6r'Ws*6=DwwUu]=C?MK [yrtܒG$!WGqJ*%SAz ED[^)/tė/g=#Omd.|^n/sl׉g DZqemqowݮRzUܜ=ڽ-o/Iۖ;qVʘgPp|mm;6zGl9.8pwWgsJ2qPbe}}UpNjٯ}7TMQKrؽtEx%v w߾8%|j;~|}pK]ơ/ w߾8%|j;~|}pK]ơ/ w&~e_H 8PL7:%ʭ5Kw&U2vwR_+rm'}C7#rWoO&HoG?M$UR7{FU]u ;# !Wk`|W>׹潇9Vn)6)*ҹ{%qV4q>W1vi#T"Qk&GwxcJBJ- Ϸ^ˁxkU}ԣ/3.;]J=<*)cS)ROK9H=,r zX @)cS)Da^ԽQ gxJI=w֣gf*TRj

#E-mail: js.hwang@gnu.ac.kr, TEL: +82-55-772-1638
• Received: March 26, 2025   • Revised: April 29, 2025   • Accepted: May 1, 2025

Copyright © The Korean Society for Precision Engineering

This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

  • 348 Views
  • 7 Download
prev next

Full Article

Download PDF Download PDF
  • Due to their structural properties, nanopatterns are actively used in various fields. In the semiconductor industry, the importance of analyzing the uniformity of nanopatterns is becoming increasingly important. New analysis methods are needed. The elliptical Fourier descriptor (EFD) method can quantify the shape information into frequency components by Fourier transforming contours. In this study, shape analysis of nanopatterns was performed using EFD. Nanopatterns with a period of about 400 nm were formed using laser interference lithography. EFD coefficients were then compared. Results of the analysis showed that the variation between coefficients of poorly shaped patterns was larger than that of normal patterns, confirming the possibility of quantitative comparison. However, further research is needed to establish a clear correlation between coefficient changes and quality changes. In the absence of a standard for geometrical changes in nanopatterns, it is expected that EFD can be applied as a methodology to provide new quantitative indicators.
  • KEYWORDS: Elliptical Fourier descriptor, Nano pattern, Uniformity, Laser interference lithography
  • KEYWORDS: 타원 푸리에 계산자, 나노 패턴, 균일도, 레이저 간섭 리소그래피

Λ

Pattern Period

λ

Wavelength of Incident Laser

θ

Angle between Incident Beam and Mirror

α

Angle of Incidence of the Incoming Radiation

β

Angle of Diffracted Radiation
나노 패턴은 특유의 구조적 특성으로 인하여, 반도체[1], 디스플레이[2], 배터리[3], 센서[4] 등 주요 산업계에서 활발하게 사용되고 있다. 특히, 반도체 업계의 경우, Extreme Ultraviolet (EUV) 광원의 도입에 따른 노드 축소가 가속화됨에 따라, 극한 수준의 품질 관리가 요구되고 있는 실정이다[5]. 또한, 국소 부위의 패턴 균일도가 전체 패턴 균일도에 점차 크게 영향을 주면서, 패턴 균일도 분석에 대한 중요성이 날로 중요해지고 있다. 일반적으로 노광된 패턴의 균일도는 패턴의 크기나 면적의 오차를 통해 측정하지만, 해당 방법의 경우, 유사한 크기나 면적을 가진 패턴의 형상적인 변화는 감지하기 어렵다는 단점을 가지고 있다. 따라서 패턴의 형상적 변화를 정량적으로 측정할 수 있는 새로운 방법론에 대한 논의와 연구가 필요할 것으로 판단된다.
Elliptical Fourier Descriptor (EFD) 방법은 폐곡선의 윤곽선을 x, y 방향에 대해 각각 하나의 비주기 신호로 생각하고, 이를 푸리에 변환하여 계수화 시키는 방법이다. 이를 통해, 전체적인 윤곽선의 형상 변화를 주파수 성분으로 정량화 하는 것이 가능하다. 기존에 주로 지리학[6], 의학[7] 분야에서 분류 용도로 활발히 활용되었으나, 반도체 업계 등 나노 패턴의 균일도를 측정하는 방법으로는 사용된 바 없는 것으로 파악되었다. 이에 따라 해당 연구에서는 EFD를 통한 나노 패턴의 형상 변화를 정량적으로 분석할 수 있는 지 실행 가능성을 탐구하였다. 나노 패턴은 상온 대기압 환경에서 비교적 손쉽게 제작이 가능한 레이저 간섭 리소그래피 공정을 이용하였다.
2.1 로이드미러 간섭계 구성
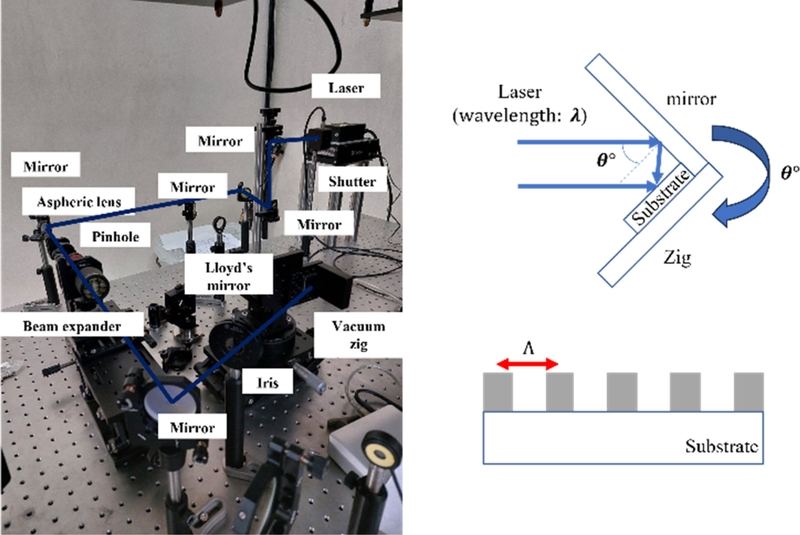
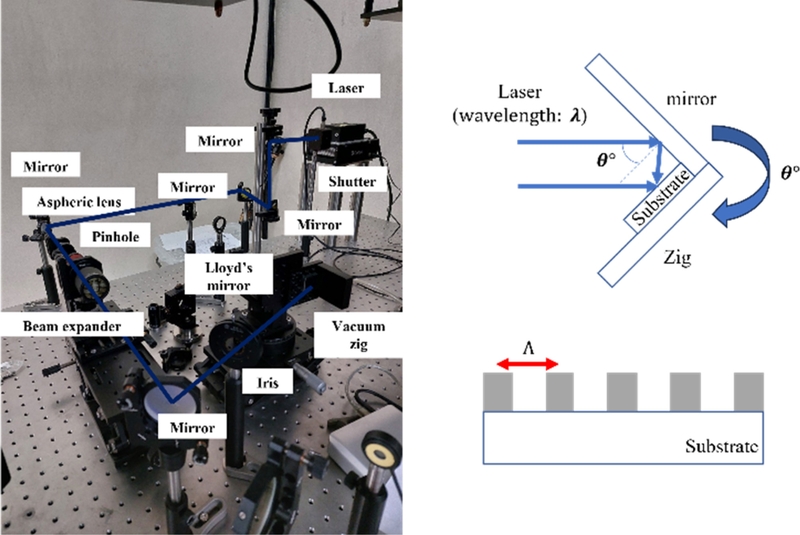
레이저 간섭 리소그래피를 수행하기 위하여, 자외선(355 nm) 광원 레이저(5 ns, 7 kHz, 125 mW, Cobolt Tor)이 사용되었다. s 편광으로 조사된 광원은 비구면 렌즈(354280-A, Focal Length f = 18.4 mm, Thorlabs)와 10-µm 핀홀(P10D, Thorlabs)을 통해서 구성된 공간 필터를 통과하여 가우시안 빔을 형성하였다. 이후, 빔 엑스펜더(BE10-355, Thorlabs)를 통과하여 약 50 mm 직경을 갖는 콜리메이션 광원을 형성하여 노광을 진행하였다. 전체 조사 시간은 자동 셔터(SH05, Thorlabs)를 통해 조절하였다. 로이드 미러 간섭계는 Fig. 1과 같이 조사된 광원과 거울에 반사된 광원을 통해 간섭 패턴을 형성하도록 구성하였으며, 회전 지그를 통하여 조사 각도를 조정할 수 있도록 구성하였다. 이때, 형성되는 간섭 패턴의 주기 Λ는 식(1)과 같이 광원의 파장 λ, 입사광과 거울의 각도 θ에 따라 결정되었다.
(1)
Λ=λ2sin⁡θ
Fig. 1.

Experimental setup and schematic of laser interference lithography

KSPE_2025_v42n6_477_f001.jpg
2.2 감광제 노광 공정
감광제 노광 및 현상 과정은 일반적인 리프트오프 공정과 동일하게 진행되었다[8]. 1인치 면적으로 준비된 유리기판(SL.Sli1012, SciLab)은 에탄올과 증류수에 5분간 초음파 세척하였으며, i-line 양성 감광제(KL5310, KemLab, USA)를 스핀 코팅(3000 rpm, 60초) 하였다. 이후 105oC에서 60초간 베이킹한 기판은 60초간 상온 대기압 환경에서 안정화하였고, 2.55 µW/cm2 조건에서 200초간 간섭광을 조사하였다. 노광 후에는 Tetramethylammonium Hydroxide (TMAH) 현상액으로 10초간 현상을 진행하였고, 이후 증류수 세척 및 질소로 물기를 제거하여 패턴을 형성하였다.
2.3 간섭 패턴 측정
간섭리소그래피를 통하여 형성된 패턴의 구조적 형상은 SEM (Evolution220, Thermo Fisher Scientific) 측정을 통하여 확인되었다. Fig. 2는 광학계 조정을 통하여 약 400 nm 주기로 라인 패턴이 형성된 기판의 형상을 보여준다. 이러한 주기적 구조는 회절 현상으로 인한 것으로, 식(2)와 같이 회절 격자에 의해 반사되는 파장 mλ는 격자의 주기 Λ와 격자에 입사되는 각도 α, 격자에서 반사되는 각도인 β에 따라 결정된다[9]. 따라서 보이는 각도에 따른 파장대의 빛을 반사하여, 구조색을 형성할 수 있다. 이와 같이 제작된 패턴의 형상적 광학적 특성을 통해, 양호한 품질의 나노 패턴이 형성된 것을 확인할 수 있었다.
(2)
mλ=Λ(sin⁡α+sin⁡β)
Fig. 2

(a) SEM image, (b) Magnified image of nanoscale line pattern from interference lithography, and (c) Structural coloration of substate

KSPE_2025_v42n6_477_f002.jpg
3.1 EFD
EFD는 폐곡선으로 형성된 이미지의 윤곽선을 각각 x방향과 y방향을 나눠서, 각각 하나의 비주기 신호로 생각을 하고, 이를 푸리에 변환하여서 푸리에 계수를 추출하는 방식으로 윤곽선을 나타낸다. 따라서 식(3) 및 식(4)와 같이 신호를 표현하는 하나의 주파수 성분에 대해서 총 4개의 계수가 추출되고, n개의 주파수 성분으로 분리하면 총 4n개의 계수가 추출된다. 해당 연구에서는 주파수를 20개 사용하여 총 80개 계수를 추출하고, 형상을 비교하였다.
(3)
xt=A0+∑n=1N ancos⁡2πntT+bnsin⁡2πntT
(4)
yt=C0+∑n=1N cncos⁡2πntT+dnsin⁡2πntT
3.2 SEM 이미지 외곽선 추출
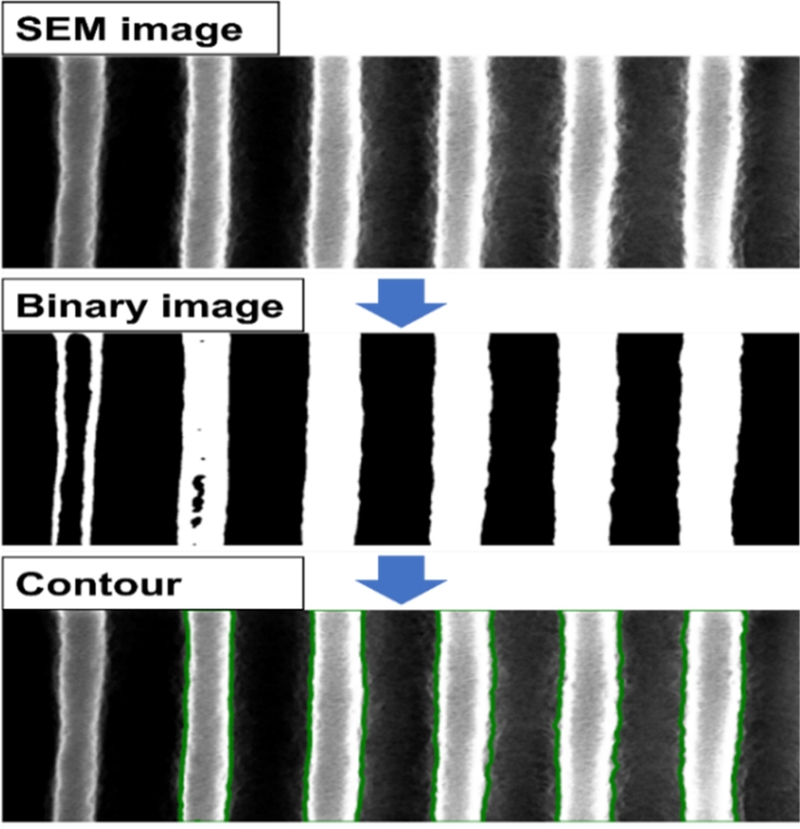
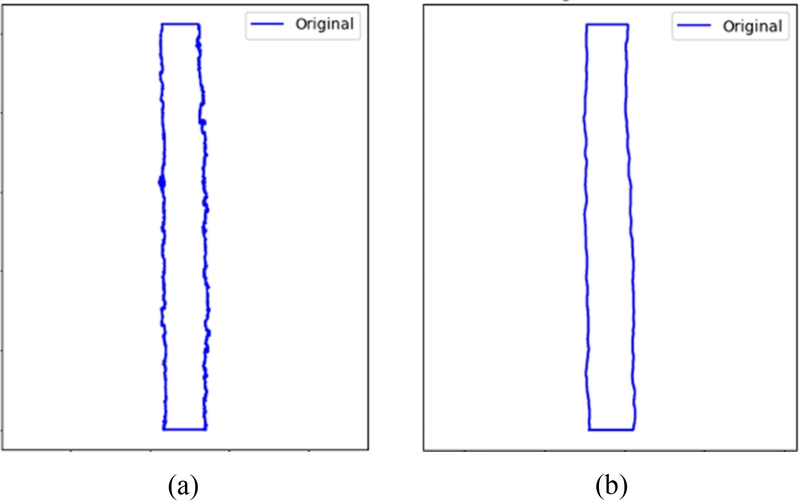
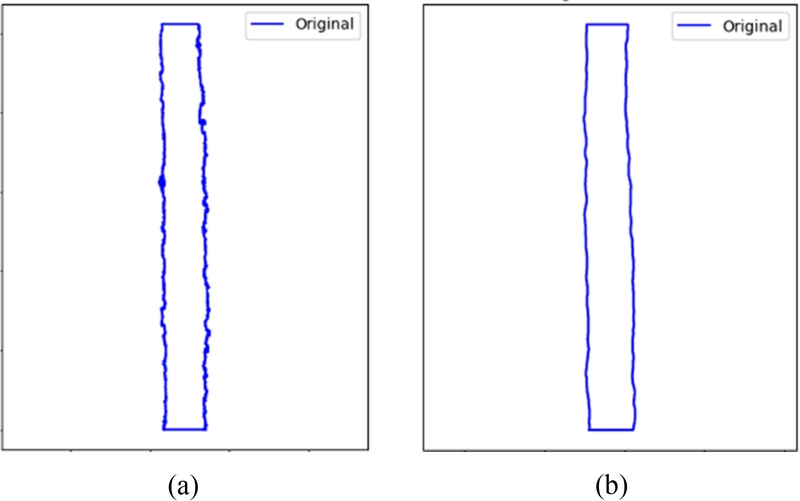
원본 SEM 이미지에서 외곽선을 추출하기 위하여 Fig. 3과 같이, 하단부 스케일을 나타내는 주석부 삭제 (Crop), 가우시안 필터를 통한 노이즈 제거(Blurring), 이진화(Binary)를 수행하고, OpenCV 외곽선 추출 함수를 이용하여 윤곽선을 추출하였다. 해당 과정에서 패턴의 전반적 형상 파악을 위해, 노이즈 제거 과정이 선행되었다. Fig. 4와 같이 원본 SEM 이미지의 윤곽선에는 고주파 성분의 변화가 나타나, 주파수 분석 시, 고주파 성분의 계수를 증가시키는 원인이 된다. 임의로 변화하는 고주파 성분의 계수를 증가시키는 것은 전체 형상 분석의 정합성을 떨어뜨릴 수 있으므로, 사전에 노이즈를 제거하였다. 노이즈 제거 후에는 일정 크기 이상의 외곽선을 추출하였고, EFD 방식에서는 반드시 폐곡선의 형상을 사용되야 하므로, 개방된 윤곽선의 경우 첫 점과 끝점을 이어서 폐곡선을 형성하였다.
Fig. 3.

Contour extraction from SEM image

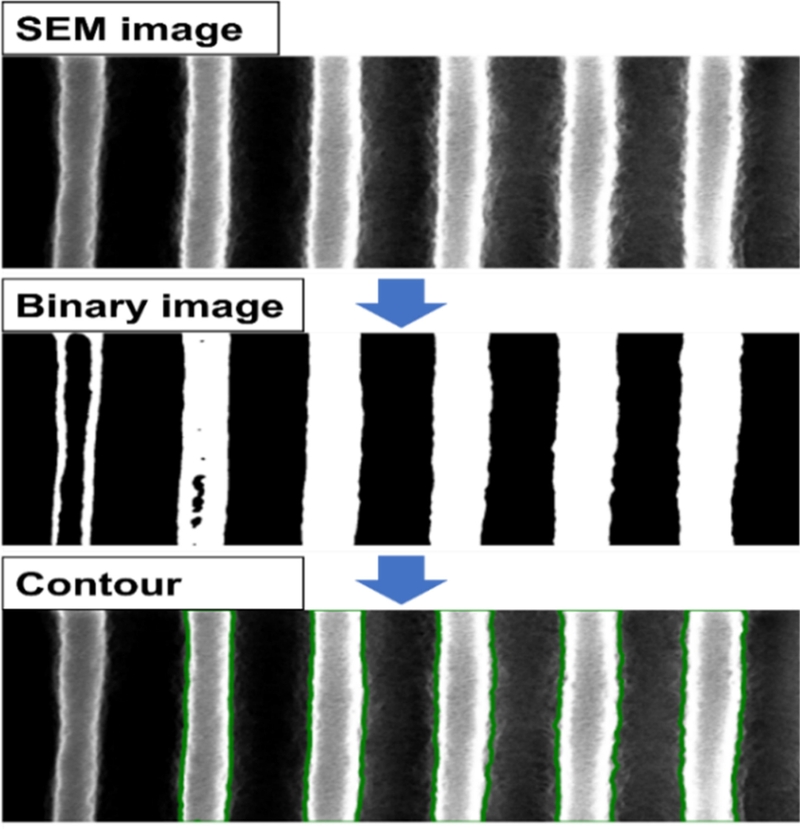
KSPE_2025_v42n6_477_f003.jpg
Fig. 4.

Extracted contour (a) before and (b) after blurring

KSPE_2025_v42n6_477_f004.jpg
3.3 EFD 계수 추출
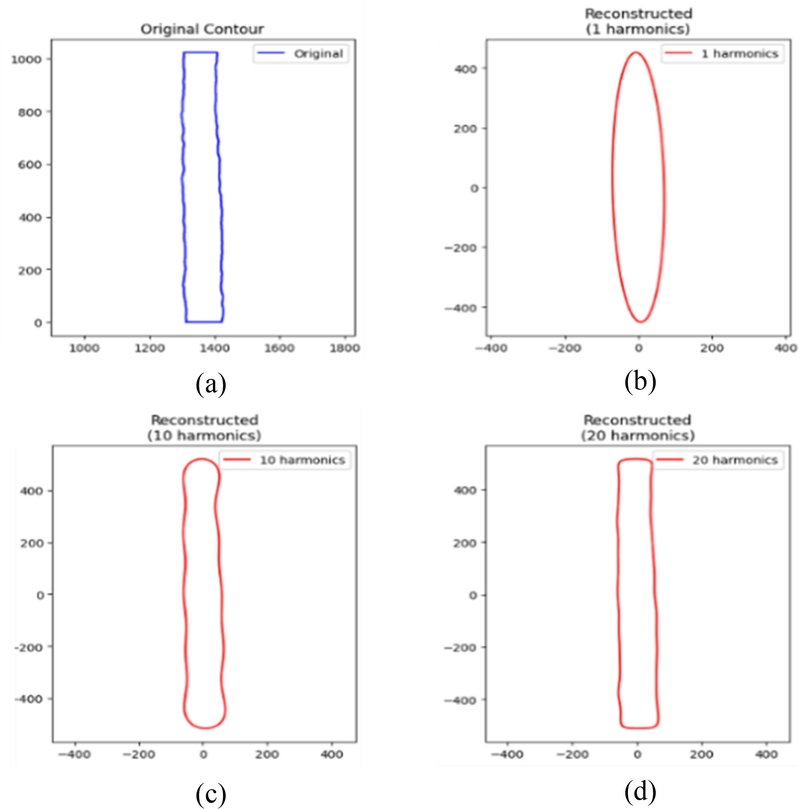
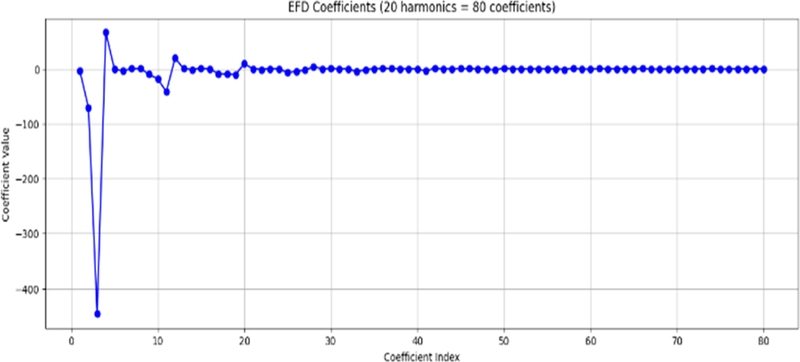
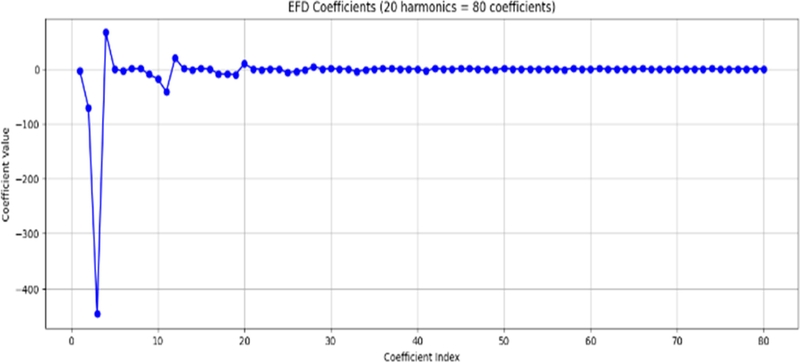
EFD 계수 추출은 PyEFP 라이브러리를 사용하였다. 추출된 계수는 Fig. 5와 같이 사용된 주파수 성분이 많을수록 원본 윤곽선의 형상을 잘 반영하는 것을 알 수 있다. 너무 많은 주파수 성분의 사용은 불필요한 계수를 생성하므로, 총 20개 주파수 성분을 사용하여 추출하였다. Fig. 6은 추출된 계수를 나타내는 것으로, 하나의 주파수에 대해서 4개의 계수가 추출되므로, 총 80개가 추출되었다. 해당 그래프를 통해 대부분의 계수들은 상대적으로 작은 값을 갖고, 특정 계수들의 영향이 큰 것을 알 수 있다.
Fig. 5.

Comparison of (a) original contour and reconstructed contours with (b) 1, (c) 10, and (d) 20 harmonics

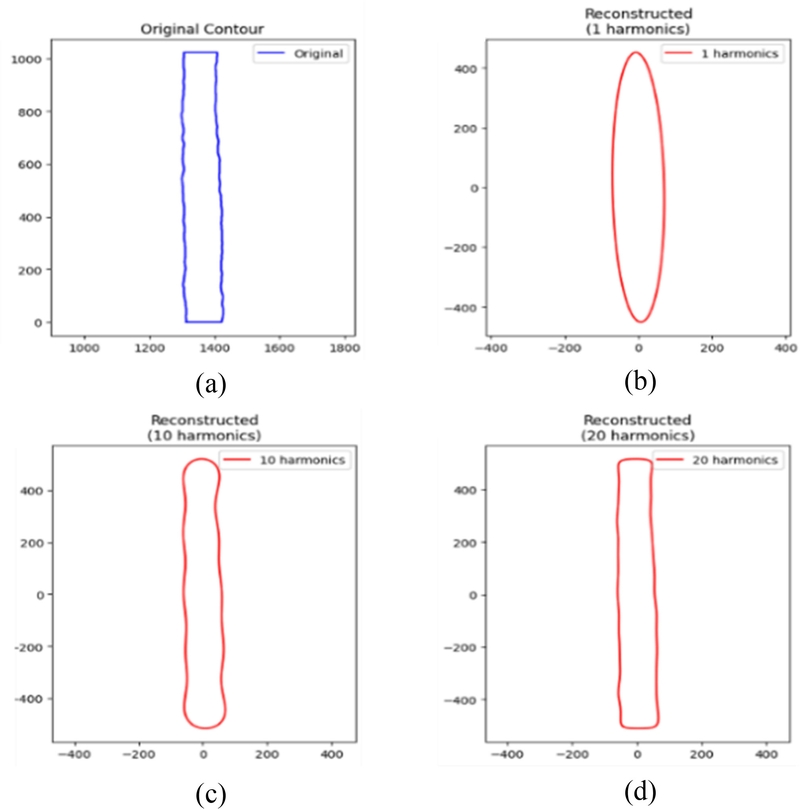
KSPE_2025_v42n6_477_f005.jpg
Fig. 6.

EFD coefficients of 20 harmonics

KSPE_2025_v42n6_477_f006.jpg
3.4 형상 변화에 따른EFD 계수 비교
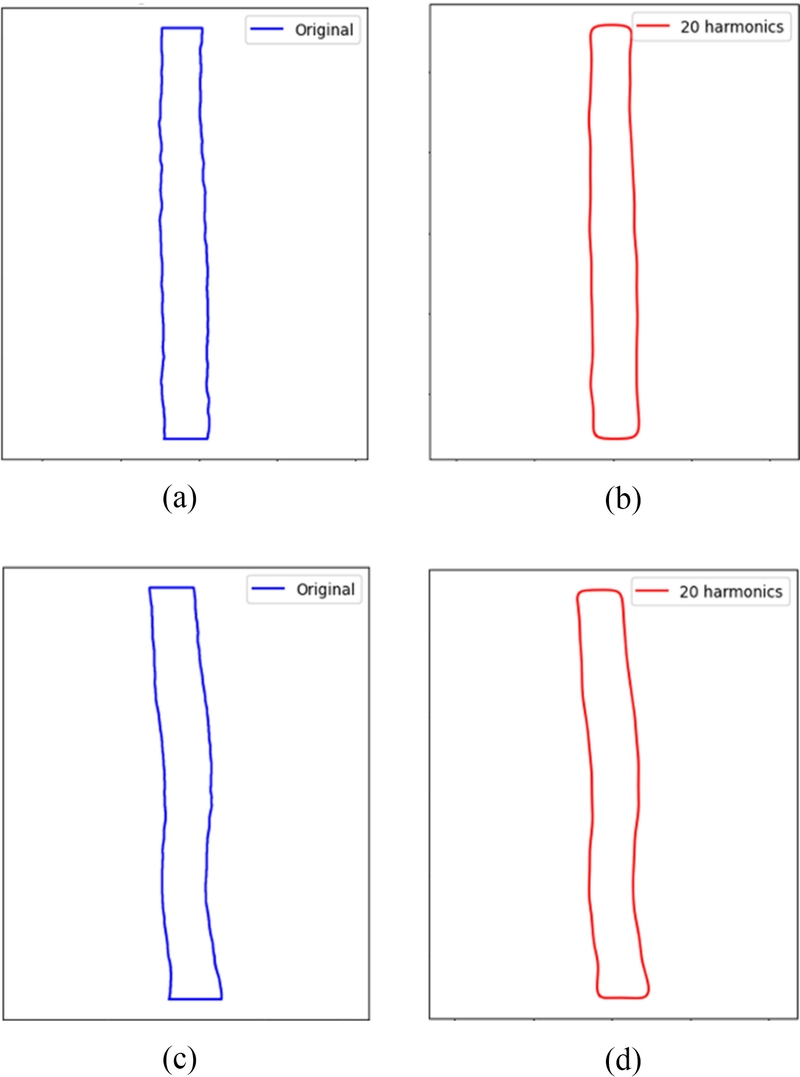
Fig. 7은 유사 패턴의 SEM 이미지들로, 일반적인 패턴과 직진도가 다소 떨어지는 패턴을 보여준다. 이 두 가지 경우에 대하여 EFD를 수행하고 계수를 비교하여, 형상 변화에 대해 정량적인 비교가 가능한지 확인하였다. Fig. 8은 각각 일반 패턴과 불량 패턴에서 추출된 윤곽선과 EFD 방법을 통해서 재구성된 윤곽선을 보여주는 것으로, 두 경우 모두 충분히 원본 형상을 반영하였다고 가정하고, 계수 비교를 수행하였다. 계수 비교 시에는 동일 조건의 윤곽선 3개에서 추출된 EFD 계수의 평균을 각각 구하고, 평균값이 1 이상의 값을 갖는 계수만 사용하여 비교하였다. 또한 평균에서 각 값을 뺀 오차의 표준 편차를 구하고, 표준편차에 3배 값을 적용하였다. 최종적으로 해당 3시그마 값이 평균에 비하여 얼만큼 큰 값을 가지는지 계산하였다. Table 1과 Table 2는 일반 패턴과 불량 패턴의 EFD 계수들의 평균과 오차의 3시그마, 3시그마와 평균의 비율을 보여준다. 이 중, 평균값 자체가 1 이하로 작아서 백분율이 커 보이는 항목을 제외하고, 평균값이 4이상인 계수를 비교하였을 때, 일반 패턴에 비하여 불량 패턴의 EFD 계수 변화 비율이 더 높은 수준을 보이는 것을 확인할 수 있었다.
Fig. 7.

Extracted contour of (a) normal and (b) defective pattern

KSPE_2025_v42n6_477_f007.jpg
Fig. 8.

(a) Original and (b) reconstructed contour of normal pattern. Defective pattern’s (c) original and (d) reconstructed contour

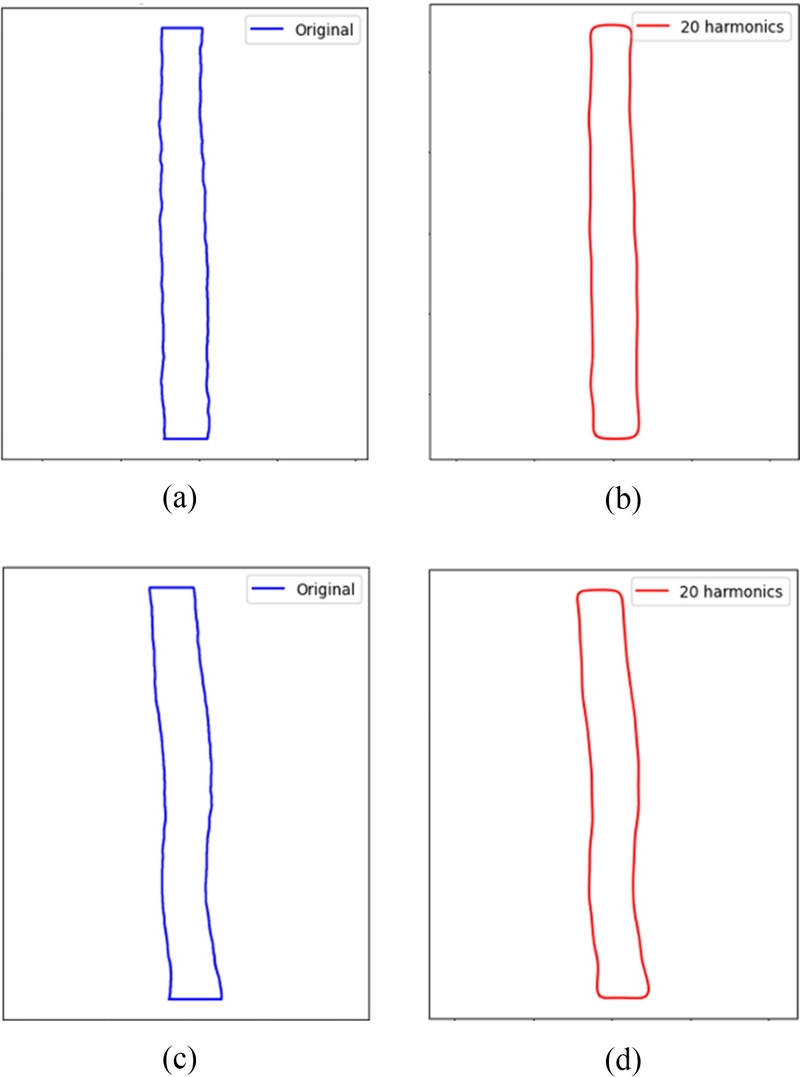
KSPE_2025_v42n6_477_f008.jpg
Table 1

EFD coefficient of normal pattern

Table 1
  Average 3sigma Percent
d1 68.59 10.24 14.93
d3 20.55 3.73 18.14
c4 9.62 1.26 13.13
d5 4.42 0.98 22.08
a6 1.54 0.67 43.59
c6 1.49 1.03 68.98
d7 1.25 0.94 74.92
Table 2

EFD coefficient of defective pattern

Table 2
  Average 3sigma Percent
d1 73.78 27.76 37.62
d3 20.92 6.46 30.85
a1 12.85 15.10 117.48
d5 9.58 1.36 14.14
d7 4.10 1.08 26.27
b15 1.27 0.91 71.90
c2 1.21 2.82 233.63
b13 1.16 2.19 189.76
d9 1.11 1.29 115.73
3.5 노이즈 여부에 따른 EFD 계수 비교
SEM 측정을 통해서 생성되는 이미지는 측정 과정에서 발생하는 각종 잡음 성분을 포함한 것으로, 전체적인 형상 파악에 무의미한 고주파 성분이 포함되어 있다. 이러한 성분의 제거를 위해 반도체 업계에서는 SEM 이미지의 Line-edge Roughness (LER) 산출 과정에서 Power Spectrum Density (PSD) 분석을 수행하고, 고주파 성분의 제거를 통한 적정 수준을 계산한다[10]. 해당 연구는 PSD의 주파수 분석과 유사하게 푸리에 급수를 통한 정량 분석을 수행하므로, 측정 원본의 노이즈에 따른 계수 변화를 비교하였다. Table 3과 Table 4는 이미지 전처리를 수행하지 않은 원본 이미지의 EFD 계수를 산출한 표로, 마찬가지로 평균 값이 1 이상인 항목을 도시하였다. 해당 결과에서는 노이즈를 제거한 Table 1과 Table 2의 계수들과 비교하였을 때, d14, d17, b19 등 상대적으로 높은 주파수 성분을 갖는 계수들이 나타나는 것을 확인할 수 있었다. 이러한 고주파 성분의 계수들은 전체적인 형상 변화를 나타내기 어려우므로, EFD 분석 과정에서 이미지 전처리를 통한 노이즈 성분의 제거가 수반되어야 함을 확인할 수 있었다.
Table 3

EFD coefficient of normal pattern without blurring

Table 3
  Average 3sigma Percent
d1 80.20 121.83 151.90
d3 28.11 11.55 41.11
d5 12.20 16.84 138.03
a2 5.99 6.01 100.29
d7 5.90 19.10 323.40
a4 3.89 1.82 46.90
c9 1.83 6.62 362.12
a6 1.79 4.20 234.99
d13 1.60 6.23 388.07
d14 1.10 2.88 269.40
Table 4

EFD coefficient of defective pattern without blurring

Table 4
  Average 3sigma Percent
d1 107.44 223.72 208.22
d3 32.26 11.47 35.56
d5 11.28 37.50 332.40
a2 7.37 21.94 297.66
d7 2.84 13.83 487.81
a4 2.33 6.01 257.63
a1 2.31 38.21 1651.72
d6 1.59 7.87 493.60
d8 1.54 13.78 894.82
d13 1.33 4.08 306.34
d17 1.20 1.96 162.94
b19 1.12 2.45 217.38
3.6 EFD 적용 예상 분야
반도체 산업에서는 종래의 사각 형태에서 원형 패턴을 적용하여 제품 품질을 향상하는 연구가 진행되고 있다. EFD는 삼각파를 기본으로 하는 함수로 원형 형태의 폐곡선을 자유롭게 표현하고, 이를 계수화할 수 있는 기법이다. 따라서, 패턴의 직진도, 비대칭성 등 형상 변화에 대한 지표로 활용 가능할 뿐만 아니라 원형 패턴의 균일도를 평가할 수 있는 새로운 지표로써 활용 잠재력이 높다고 판단된다.
다만, 현재 연구에서는 형상 변화와 특정 계수 간의 명확한 상관관계, 계수 변화에 대한 소자 성능의 상관성 등 명확한 해석을 위해서는 추가적인 연구가 필요할 것으로 보인다. 이를 위해, 패턴 형상의 변화에 따른 소자 성능과 EFD 계수 간의 관계를 유추하는 회귀분석, 딥러닝 등을 적용하여 형상 변화를 정량적으로 예측할 수 있는 새로운 방법론으로 적용될 수 있을 것이라 기대된다.
나노 패턴의 형상에 대한 정량적 품질 비교를 위해 EFD 방법을 적용하였다. 나노 패턴 제작을 위하여 레이저 간섭 리소그래피를 이용하여 약 400 nm 정도의 주기를 갖는 나노 패턴을 형성하였으며, SEM 측정을 통해서 관찰된 이미지의 전처리를 통해 윤곽선을 추출하였다. 최종적으로 해당 윤곽의 EFD 계수 추출을 통하여, 제작된 패턴의 형상 변화에 대해 비교하였다. 계수 비교를 통하여 패턴 형상이 불량한 패턴의 경우 비교적 계수 간의 변화 폭이 일반 패턴에 비하여 크게 나타나, 정량 비교 가능성은 확인하였으나, 계수 변화와 품질 변화에 대한 명확한 상관 관계를 밝히기 위해서는 추가적인 연구가 필요할 것으로 파악된다. 나노 패턴의 형상적 변화에 대한 기준이 부재한 현재 상황에서, 새로운 정량 지표를 제시할 수 있는 방법론으로EFD가 적용될 수 있을 것이라 기대된다.
이 연구는 한국기초과학지원연구원 신진연구자 인프라 지원사업(No. RS-2024-00402192)의 지원을 받아 수행되었음.
  • 1.
    Chen, Y., Song, C., Gao, J., Li, X., (2024), Past progress, current status, and future perspective of digital euv lithography for high-resolution semiconductor manufacturing, Novel Patterning Technologies 2024, 12956, 184-199.
    10.1117/12.3010567
  • 2.
    Feng, J., Liu, Y. F., Bi, Y. G., Sun, H. B., (2017), Light manipulation in organic light-emitting devices by integrating micro/nano patterns, Laser & Photonics Reviews, 11(2), 1600145.
    10.1002/lpor.201600145
  • 3.
    Cho, S., Jung, W., Jung, G. Y., Eom, K., (2020), High-performance boron-doped silicon micron-rod anode fabricated using a mass-producible lithography method for a lithium ion battery, Journal of Power Sources, 454, 227931.
    10.1016/j.jpowsour.2020.227931
  • 4.
    Ahn, H.-J., Thiyagarajan, P., Jia, L., Kim, S.-I., Yoon, J.-C., Thomas, E. L., Jang, J.-H., (2013), An optimal substrate design for sers: Dual-scale diamond-shaped gold nano-structures fabricated via interference lithography, Nanoscale, 5(5), 1836-1842.
    10.1039/c3nr33498h
  • 5.
    Lee, H., Lee, J., Lee, D., Nam, I., Lee, S., (2024), Readiness for predictive maintenance of high cost EUV equipment using big data, Photomask Japan 2024: XXX Symposium on Photomask and Next-Generation Lithography Mask Technology, 200-208.
    10.1117/12.3032128
  • 6.
    Dhingra, R. D., Barnes, J. W., Hedman, M. M., Radebaugh, J., (2019), Using elliptical fourier descriptor analysis (EFDA) to quantify titan lake morphology, The Astronomical Journal, 158(6), 230.
    10.3847/1538-3881/ab4907
  • 7.
    Caple, J., Byrd, J., Stephan, C. N., (2017), Elliptical fourier analysis: Fundamentals, applications, and value for forensic anthropology, International Journal of Legal Medicine, 131(6), 1675-1690.
    10.1007/s00414-017-1555-0
  • 8.
    Zhou, Y., Chen, X., Fu, Y., Vienne, G., Kuznetsov, A., Luk’Yanchuk, B., (2013), Fabrication of large-area 3d optical fishnet metamaterial by laser interference lithography, Applied Physics Letters, 103(12).
    10.1063/1.4821508
  • 9.
    Jwad, T., Penchev, P., Nasrollahi, V., Dimov, S., (2018), Laser induced ripples’ gratings with angular periodicity for fabrication of diffraction holograms, Applied Surface Science, 453, 449-456.
    10.1016/j.apsusc.2018.04.277
  • 10.
    Rutigliani, V., Lorusso, G. F., De Simone, D., Lazzarino, F., Rispens, G., Papavieros, G., Gogolides, E., Constantoudis, V., Mack, C. A., (2018), Setting up a proper power spectral density (psd) and autocorrelation analysis for material and process characterization, Metrology, Inspection, and Process Control for Microlithography XXXII, 367-374.
    10.1117/12.2297264
June Sik Hwang
KSPE_2025_v42n6_477_bf001.jpg
Assistant Professor in the Department of Mechanical Engineering, Gyeongsang National University. His research is advanced laser processing.
Ha Seong Joo
KSPE_2025_v42n6_477_bf002.jpg
Undergraduated from the Department of Mechanical Engineering, Gyeongsang National University. His research is laser patterning.
Huseung Lee
KSPE_2025_v42n6_477_bf003.jpg
Professor in the Department of Mechanical Engineering Education, Chungnam National University. His research is material properties-based machining and assembly.

Download Citation

Download a citation file in RIS format that can be imported by all major citation management software, including EndNote, ProCite, RefWorks, and Reference Manager.

Format:

Include:

Analysis of Nano Pattern Uniformity based on Elliptical Fourier Descriptor Method
J. Korean Soc. Precis. Eng.. 2025;42(6):477-482.   Published online June 1, 2025
DOI: https://doi.org/10.7736/JKSPE.025.046
Download Citation

Download a citation file in RIS format that can be imported by all major citation management software, including EndNote, ProCite, RefWorks, and Reference Manager.
Format:
Include:
Analysis of Nano Pattern Uniformity based on Elliptical Fourier Descriptor Method
J. Korean Soc. Precis. Eng.. 2025;42(6):477-482.   Published online June 1, 2025
DOI: https://doi.org/10.7736/JKSPE.025.046
Close

Figure

  • 0
  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
Analysis of Nano Pattern Uniformity based on Elliptical Fourier Descriptor Method
Image Image Image Image Image Image Image Image
Fig. 1. Experimental setup and schematic of laser interference lithography
Fig. 2 (a) SEM image, (b) Magnified image of nanoscale line pattern from interference lithography, and (c) Structural coloration of substate
Fig. 3. Contour extraction from SEM image
Fig. 4. Extracted contour (a) before and (b) after blurring
Fig. 5. Comparison of (a) original contour and reconstructed contours with (b) 1, (c) 10, and (d) 20 harmonics
Fig. 6. EFD coefficients of 20 harmonics
Fig. 7. Extracted contour of (a) normal and (b) defective pattern
Fig. 8. (a) Original and (b) reconstructed contour of normal pattern. Defective pattern’s (c) original and (d) reconstructed contour

Fig. 1.

Fig. 2

Fig. 3.

Fig. 4.

Fig. 5.

Fig. 6.

Fig. 7.

Fig. 8.

Analysis of Nano Pattern Uniformity based on Elliptical Fourier Descriptor Method
  Average 3sigma Percent
d1 68.59 10.24 14.93
d3 20.55 3.73 18.14
c4 9.62 1.26 13.13
d5 4.42 0.98 22.08
a6 1.54 0.67 43.59
c6 1.49 1.03 68.98
d7 1.25 0.94 74.92
  Average 3sigma Percent
d1 73.78 27.76 37.62
d3 20.92 6.46 30.85
a1 12.85 15.10 117.48
d5 9.58 1.36 14.14
d7 4.10 1.08 26.27
b15 1.27 0.91 71.90
c2 1.21 2.82 233.63
b13 1.16 2.19 189.76
d9 1.11 1.29 115.73
  Average 3sigma Percent
d1 80.20 121.83 151.90
d3 28.11 11.55 41.11
d5 12.20 16.84 138.03
a2 5.99 6.01 100.29
d7 5.90 19.10 323.40
a4 3.89 1.82 46.90
c9 1.83 6.62 362.12
a6 1.79 4.20 234.99
d13 1.60 6.23 388.07
d14 1.10 2.88 269.40
  Average 3sigma Percent
d1 107.44 223.72 208.22
d3 32.26 11.47 35.56
d5 11.28 37.50 332.40
a2 7.37 21.94 297.66
d7 2.84 13.83 487.81
a4 2.33 6.01 257.63
a1 2.31 38.21 1651.72
d6 1.59 7.87 493.60
d8 1.54 13.78 894.82
d13 1.33 4.08 306.34
d17 1.20 1.96 162.94
b19 1.12 2.45 217.38
Table 1 EFD coefficient of normal pattern
Table 2 EFD coefficient of defective pattern
Table 3 EFD coefficient of normal pattern without blurring
Table 4 EFD coefficient of defective pattern without blurring

Table 1

Table 2

Table 3

Table 4

JKSPE : Journal of the Korean Society for Precision Engineering

ABOUT

BROWSE ARTICLES

EDITORIAL POLICIES

FOR CONTRIBUTORS

© Korean Society for Precision Engineering.